基于音樂中的自相似性原則

肖武雄

摘要：該文從音律學切入，精確到四十八平均律中去探究音樂結構的自相似性問題，推導建立自相似性音樂分析的參數設定，并以作曲家陳曉勇鋼琴小品《日記I》為例進行求證。

關鍵詞：自相似；維度；分數維；域；陳曉勇

中圖分類號：J614.5文獻標識碼：ADOI：10.3969/j.issn1003-7721.2014.03.004

自相似性是混沌學最主要的理論成果之一。意思是：宇宙中的萬事萬物，其內部（部分）與整體之間從不同的空間尺度或時間尺度來看都存在相似性。比如自然界中的油漆、泥裂、云、雞冠花、花椰菜、樹葉，醫學界的無性繁殖、基因克隆……。同樣，音樂藝術領域中自相似性早已存在，主要通過作品的組織結構及音響再現表現出來。如貝多芬的“動機分裂”，勛伯格的“主題一致性”，基本樂理中的音程特征，傳統和聲學中的三和弦、七和弦無不是自相似性的表現。從音樂分析的角度出發，自相似性應該解構到構成作品的最小單位，類似于電子圖形學中的“取樣精度”。隨著歷史的進程，這種取樣精度同樣在音樂作品中有相應的表現。比如：漢族五聲性調式的自相似性，從音程角度看是通過大二、小三、大三、純四度及它們的轉位音程表現的；七聲性調式音級是以小二、大二、小三、大三、純四、增四度及它們的轉位音程表現的；十二平均律的自相似音程本質上也是這六個；二十四律的本質音程是在六個特征音基礎上再增加六個微分音共十二個音組成。即：

此處的“音素”是以傳統樂理計算，即：1/4表示四分之一音，1/2表示二分之一音，1為全音。 來表現。

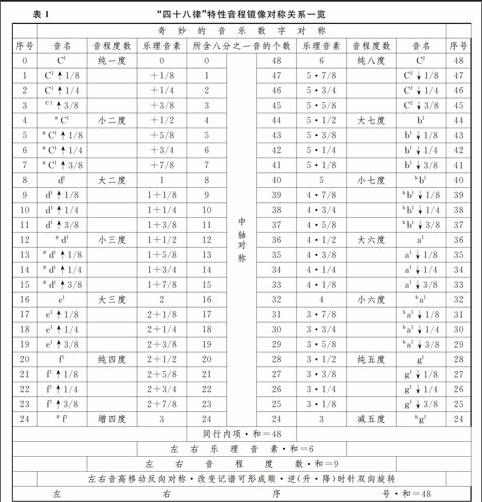
同理，四十八律就有二十四個特征音程構成本質因素。（見表1）

表1把C1至C2一個八度音域空間均分為四十八份，每一個最小單位為八分之一音。傳統樂理記為1/8，即C1至C2共48個1/8。以中軸為準，左右兩側嚴格鏡像對稱，逆時針旋轉音程逐漸增加一個單位（1/8），順時針旋轉音程逐漸減少一個單位（1/8）。#f與bg為等音，音程含量與序號都完全一樣。

以上計算了一個八度（六個全音）按照十二、二十四、四十八平均律劃分的情況，

即：6×1=6（一個八度有六個全音）

12×1/2=6（一個八度有十二個半音）

24×1/4=6（一個八度有二十四個四分之一音）

48×1/8=6（一個八度有四十八個八分之一音）

表1“四十八律”特性音程鏡像對稱關系一覽

奇妙的音樂數字對稱

序號音名音程度數樂理音素所含八分之一音的個數樂理音素音程度數音名序號

神奇的6！無論怎么劃分（按偶數、奇數、質數做均分）都能得到中軸對稱的音列。而且，永遠能分割下去——日取其半，萬世不竭。

即：一個八度包含6n 個 1/n ， [ n ∈ ∞ ]

數學表達為：6n × 1/n = 6

由此可見：音樂的自相似性是由“數”這里的“數”針對不同的對象有不同的表現，從音程而言表現為整數、分數；從聲音頻率、振幅而言表現為整數、小數；從三者的關系而言表現為對數、函數；從空間及聲音相位而言表現為度數、正數、負數…… 來表現的，“數”是音樂的根本。如畢達哥拉斯所言：“音樂的美與和諧只能到‘數的關系去尋找”羅塞夫：《古代音樂美學》，莫斯科國家音樂出版社，1960年第1版 ，第16頁。 。那么，音樂與數還有什么關系呢？音樂作品中的自相似性如何表達？何為它的最小單位？最小單位如何包含預示整體的屬性？要解釋這些問題必須先搞清楚兩個概念。

1.維度（ dimension ）

維度就是我們分析的目標對象所采用的分析角度，又稱維數，是數學中獨立參數的數目。在物理學和哲學的領域內，指獨立的時空坐標的數目 。

點：是0維，沒有長度。表明音樂中絕對的“點”（靜止的單音）所謂絕對的“點”結構，只起靜止的譜面意義，一旦它觸發振動就會有從生到死（發音到消失）的全過程，這一過程中存在許多諧波泛音，所以樂音中的“絕對單音”是不存在的。 是不存在的。

線：是1維，只有長度。表示音樂中的音程距離，如微分音，自然音程等等。

面：是2維，由長寬的兩條直線（或曲線）構成的面積。表明任意音向空間兩個方向發展都會出現的相應面積。

體：是3維，由長寬高三條相交的直線（或曲線）構成。表明任意音向空間三個方向發展都會出現的相應體積。

場：是4維，三維的世界是靜止的，當三維世界以時間為基準發生變化時，四維空間就產生了，如果把時間看作一根軸線，則這個軸線上的任意一個點，都是一個三維空間，也就是說無數個三維空間依據時間軸線集合，構成了四維空間。

傳統樂理把自然音程限定在十四種之內，即：“一四五八無大小，二三六七沒有純，外加增四減五”晏成佺、童忠良：《基本樂理教程》，北京：人民音樂出版社2006年版。 。同樣，把音樂演奏的時間最低細化到“秒”。這些單位對于極限認識的分形理論而言太過“粗糙”，不準確。當代科技的測試手段，要求各參數精密計算，更加細化，從而找到“最小的自相似性”。認識從極限更接近事物的本源。

2.分數維（fractal dimension ）

19世紀，數學家們發現了分形，由此創立了一種新的維度——“分數維”，人們由此意識到，維度不只是整數，還有可能是分數，甚至可能是無理數！英國著名物理學家史蒂芬·霍金教授有這樣的解釋：這就像一根頭發，遠看是一維的線，在放大鏡下，它確實是三維的；如果面對時空，如果有足夠高倍的放大鏡的話，也應該能揭示出其它可能存在的4維、5維空間，直至11維空間。相對于音樂而言微分音就是分數維，理論上可以細分到無窮，即：1/∞。但是，從人們可以感覺和演奏的角度出發，微分音到1/8精度，從創作和演奏上說就已經夠用了。從律學角度上說卻還需要精細到1/200精度，這正好是一個音分的單位，也是全世界律學通行的精度單位。盡管微分音還可以細分下去，那也是運用于軍事科學領域，于音樂作品而言反倒成為了累贅，故而，基本不用。

時間維度，同樣可以精細到微妙、納秒……，但針對音樂組織的頻譜分析軟件使用的最小單位是毫秒。它們的關系如下：

1s（秒）=103ms（毫秒）=106μs（微秒）=109ns（納秒）

3.域（domain）

域本身也是一種維度，指客觀事物存在的空間范圍（靜態和動態兩種范圍）。一切聲源都在震動，所以，構成音樂作品的任意一個組織參數都是運動的。音樂藝術領域涉及的域及維度都是具有生命的，具有自身的起始過程，其過程之中反映出的相對穩定屬性更值得我們重視。總譜記錄的只是譜面靜態的域，需要在二度創作變成音響時，才能實現動態而富有生命的域。

點：就是“無”，沒有運動，沒有生命，也沒有域。即：零時空。

線：對應“線域”，在一維條件下，大無終，小也無終（極限接近零）。

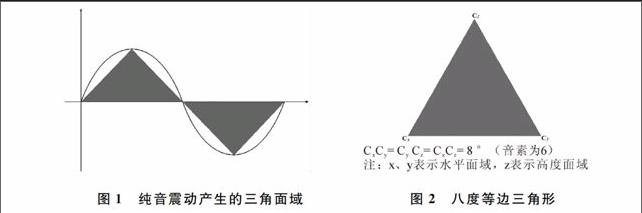
面：對應“面域”，只要琴弦震動，無論琴弦多長，哪怕它短到極限，它也有波峰、波谷及平衡中點，倘若把三者連接起來得到的就是二維面域。（見圖1）

圖1純音震動產生的三角面域圖2八度等邊三角形

我們已知樂音中包含N個純音，即：琴弦全長震動時，弦上的“N段點”都能產生自己的諧波泛音，所有各段的震動都能構成屬于自己的“三角面域”，微分音構成微分三角形，全音程構成全音三角形……下面取一個等邊三角形來進一步研究。假設邊長等于一個八度。（見圖2）

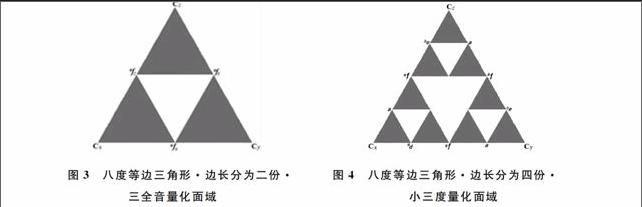
下面取各邊長的中點，即：增四（減五）的三全音點（音素為3）把它們構成的三角形挖空。（見圖3）

圖3八度等邊三角形·邊長分為二份·圖4八度等邊三角形·邊長分為四份·

三全音量化面域小三度量化面域

同理，再繼續剩余三角形邊長的一半，量化精度到增二（小三）度（音素為112）。（見圖4）

再取所得三角形邊長的一半，量化精度到四分之三音（音素為3/4）。（見圖5、6）

圖5八度等邊三角形·邊長分為八份·圖6八度等邊三角形·邊長分為十六份·四分之三度量化面域八分之三度量化面域

繼續取更小的量化單位十六分之三，邊長分為三十二份·還可以得到下列三角形（見圖7）：

圖7圖8八度等邊三角形·邊長均分五份·

一又五分之一音素量化面域

這樣的極限劃分可以永遠進行下去，從音樂實際演奏的角度到這一步就夠用了。這一圖形原理運用了謝爾賓斯基“墊片”理論波蘭數學家謝爾賓斯基（W.Sierpinski1882—1969 ）以對集合論、數論和拓撲學的出色貢獻而聞名，他在1915年提出了墊片理論，是自相似集的一種 。 。上述三角形都是按照“找中點二分法”（類似傳統樂理音值組合的基本劃分）不斷地向下進行。倘若是把邊長按照奇數劃分，如分為：三、五、七、九、十一………………得到的三角形還會是等邊三角形嗎？（見圖8）

均分三、七、九、十一…結論一樣，推理略。

可見：得到的仍然是等邊三角形，它就相當于基本樂理中音值組合法的特殊劃分。

在此，不禁要問，有無不等邊三角形，倘若只有一個邊長做任意數目的均分，從該邊長外的第三維點（原三角形的高點）向各分段點連線，得到的三角形就是不等邊三角形。（見圖9）

圖9八度等邊三角形·邊長奇數圖10四面體三角形謝爾

劃分得到不等邊三角形量化面域賓斯基 “墊片”量化體域

從圖9各維出發得到的都是三角形，即便由維線相交得到的梯形及更加復雜的多邊形，也可以繼續劃分都能找到更小單位的三角形組織。

從上述推理可以得到下列結論：

1.音樂作品的自相似性在面域上音樂作品的自相似性在線域上是以音程度數（音素）表示的，通常以作品中的最小音程數為單位。 是通過三角形表現（即使在任意小的比例尺度內也包含整體）。

2.任意三角形的三個頂點構成一個三和弦，四邊形（梯形）可分為兩個三角形。即：傳統七和弦可以拆分為兩個三和弦。

3.N面體最少包括N個三和弦，極限劃分存在無窮個三和弦。

4.音響的存現形式是立體的，具有時空屬性。上述所有三角形的劃分都是在“靜態場景”（譜面意義）中的分形壓縮。實際運用還需要考慮音響的多維屬性。

5.音樂就是三角形（三和弦）的集合可能有人會反問，如單一聲部獨奏，三角形在哪里？傳統譜面記錄的單旋律表面看是一維曲線，實際上是立體四維時空呈述，用頻譜儀可以把每一個階段參數記錄下來。通俗地說就是：音響是以聲場的傳輸轉移來實現的，譜面旋律的任何一個單音都構成以它為基音的諧波系列（聲場），旋律音響是聲場的有序集合。 。

6.陰陽、生死、分合、虛實體現分形構成的空間秩序和永恒法則。（見圖10）

由此，可見音樂音響分析的難度。

因為自相似性在任何時期、任何流派、任何作曲家的作品中都大量存在，僅僅是名詞使用不同而已，無需贅述。下面僅以陳曉勇鋼琴小品《日記I》第一首《上發條的小雞》（Clockwork Chicken）為例，從線域、面域、體域角度尋找作品的自相似性。

作品的核心材料來源于三個音，整個作品是由“g-ba-a-bb”四個音構成的四面立體時空體域構成，四面分別是：bb-a-g、bb-g-ba、b-a-ba、ba-a-g，再由它們閉合成一個四面體。見下圖：

線域特征面域特征體域特征

圖11陳曉勇《上發條的小雞》線域一、面域一、體域將位示意

通過樂譜可見，作品可以分為三個段落。

A.呈示段

1.面域呈示：由“g-bb-a”三角形構成，演奏音色使用兩種方式： ①抑制音（dampened）奏法用左手摁住琴弦，抑制弦振動，盡量發出只有音頭的干音。 ，樂譜記為實音黑符頭②余音（正常完全振動ordinary）奏法琴鍵觸弦瞬間，左手立刻離開琴弦，讓琴弦充分振動，發出所有諧波泛音。 ，樂譜記為方塊符頭。原型呈示以后，緊接著逆行呈示。

譜例1陳曉勇《Clockwork Chicken》呈示段核心材料面域呈述

2.體域呈示：由“g-bb-ba-a”四面體構成。體域呈示以后又回“g-bb-a”三角形構成的面域呈示。可見，呈示段本身具有“再現性”。

B.派生中段

如果說呈示段是演奏法的一維線性呈述，那么派生中段就是演奏法的二維對位，即把呈示段的兩種演奏法“化橫為縱”形成“虛實相映”的對比復調二維呈述。

譜例2陳曉勇《Clockwork Chicken》派生中段演奏法二維對比

譜例2中上方聲部持續的a音是一道看不見的風景，下方的“bb-g”形成的循環斷奏由于抑制了琴弦振動，只發出基頻音高，而幾乎沒有泛音。相反由于a鍵琴弦共振而產生一系列諧波泛音，也就是說a弦成為了bb-g的共鳴箱，而bb-g兩弦是發生器。

可見，譜面的風景是“實比虛好看”，實際音響畫面卻是“虛比實精彩”，這從又一個側面證明了作曲家喜歡的隱性原則。中段不停地用“a-ba”兩音來做虛軸共鳴，實音抑制演奏保持呈示段特點，在另外兩個（或三個）音點上輪回，整體始終保持面域（或體域）特征。

C.總結性綜合變化再現

再現對映呈示也具有三部性原理。

1.面域再現：由“g-bb-a”三角形構成，先回到演奏法（抑制音與余音），一線呈述方式。

2.體域再現：演奏法虛實二維對位，虛用加法，增加為四個音。實用減法，先用“bb-a”兩音，再逐漸拉長稀釋停到bb音上，收攏全曲。

上述分析可見：三角形自相似性分析能夠幫助我們從立體時空角度去把握作品的組織結構，把譜面靜態場景的音高變成多維時空，立體地呈現出來。從而讓我們發現許多傳統分析無法觸及的領域。

值得注意的是：自相似性分析所提煉的參數單位要相對統一。比如上述各例是從音高角度分析，還可以從音色、力度、時值、相位、密度……各參數分析。倘若混合參數，分析將更加繁雜。

自相似作為對稱性的一種，是科學地或者哲學地把握世界的一種范式、工具。它打破了整體與部分之間的隔膜，找到了部分過渡到整體的媒介和橋梁——整體與部分之間的相似。是古代哲學思想在近代自然科學中的重現：

一性圓通一切性，一法遍含一切法。一月普現一切月，一切水月一月攝。

——玄覺《永嘉證道歌》玄覺：《永嘉玄覺禪師證道歌講析》，成都：四川巴蜀書社2006年版。

這種在一刻鐘把握永恒，“一沙見世界，一花窺天堂”的自相似性是藝術作品自我組織的根本原則。同時，我們也要清醒地認識到分形理論不是萬能的，它只是一種方法或規則。在事物整體之中還存在著驚異的混沌。

（責任編輯：張璟）