基于數字樣機技術的鏈傳動運動學分析
尚 歌
SHANG Ge
(吉林建筑大學,長春 130118)
0 引言
鏈傳動是機電產品中常用的一種傳動形式,它品種繁多,應用廣泛。但由于鏈傳動的獨有運動特性-多邊形效應的存在,致使鏈傳動運動時不能保持恒定瞬時傳動比,使鏈條與鏈輪容易產生沖擊、振動和噪聲[1]。不但使傳動速度下降,磨損嚴重,還對鏈條具有破壞作用,使鏈傳動在有運動平穩性要求和轉速較高的場合的使用受到了限制[2]。因此,對鏈傳動運行學的研究具有非常重要的意義。
數字樣機可以代替實物樣機實現對機械系統的運動學分析,并且已在多種復雜機械系統中得到廣泛的應用,這也為研究鏈傳動的運動學特性提供了有效的研究手段。為此,本文基于數字樣機技術,建立了鏈傳動的運動仿真模型,采用仿真模擬,對鏈傳動的運動學特性進行了分析與研究。
1 鏈傳動的運動學特性
在仿真之前,先對其運動特性進行數學分析,明確鏈速、傳動比等各參變量之間的關系,找出多邊形效應的影響因素,從而為在數字樣機中作進一步分析打下基礎。
由于鏈傳動存在多邊形效應,即使主動輪以等角速度轉動,傳動鏈條的線速度和從動輪的角速度也是變化著的,同時這種變化是周期性的[3]。
1.1 鏈條的速度變化
現通過主動鏈輪上嚙入鏈節鉸鏈的運動來分析鏈速的變化。為便于分析,設鏈輪在工作時,主動邊始終處于水平位置。圖1所示為鏈傳動的速度分析圖。
當鏈節進入嚙合時,鉸鏈A隨鏈輪作圓周運動,其圓周速度vA為:

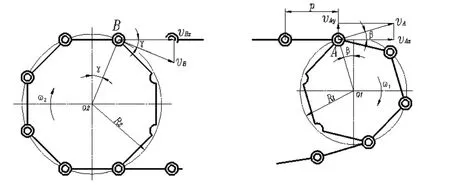
圖1 鏈傳動的速度分析圖
其中,R1為主動鏈輪的分度圓半徑;
ω1為主動鏈輪的角速度。
沿鏈條前進方向的分速度(鏈條速度)vAx和垂直鏈條前進方向的分速度vAy為:

β為嚙入過程中鏈節鉸鏈在主動輪上的相位角,其變化范圍是-180°/z1~180°/z1,z1為主動鏈輪齒數。

由上文可知,即使主動鏈輪作等速轉動,鏈條速度也將隨相位角的變化作周期性變化。
1.2 從動鏈輪的角速度變化
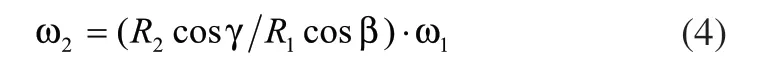
其中,R2為從動鏈輪的分度圓半徑;
ω2為從動鏈輪的角速度。
γ為鏈節鉸鏈在從動輪上的相位角,其變化范圍是-180°/z2~180°/z2,z2為從動鏈輪齒數。
當 0=β ,γ=± (180°/z2) 時,
由此可知,從動輪角速度仍呈周期性變化。
1.3 瞬時傳動比
由式(4)導出,瞬時傳動比is為:

鏈傳動的瞬時傳動比is也在不斷變化。
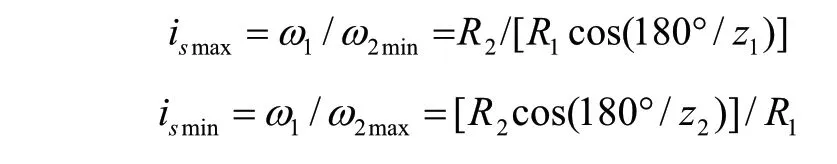
只有在z1=z2,且中心距a為節距p整數倍時,瞬時傳動比才保持恒定值is=1。但此時鏈速的不均勻性并沒有消除。
綜合上述的分析,鏈條運動的不均勻性與鏈輪的大小,及β角和γ角的變化范圍有關,也就是與鏈條節距和鏈輪齒數有關。因此,在下面的仿真中,將針對鏈傳動速度變化、鏈條節距和鏈輪齒數對鏈速的影響進行研究。
2 鏈傳動的運動仿真
因為滾子鏈使用最廣,所以本文將以滾子鏈為研究對象,通過Catia DMU(數字樣機)的運動機構模塊實現其動作,然后對其運動特性進行分析。運動仿真流程圖如圖2所示。
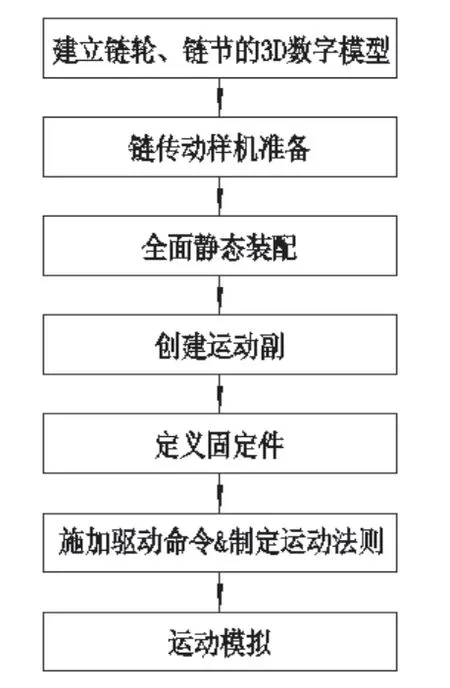
圖2 運動仿真流程圖
鏈傳動裝配及仿真模型如圖3所示。
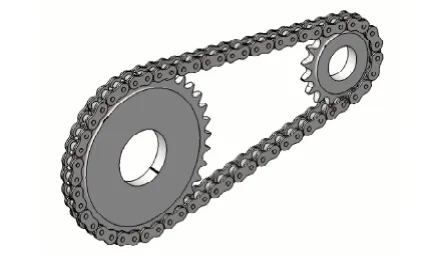
圖3 鏈傳動裝配及仿真模型
下面對仿真結果進行分析。
3 鏈傳動的運動仿真結果分析
基于鏈傳動的運動仿真結果分析,找出其運動變化規律。鏈傳動仿真模型的主要參數如表1所示。

表1 鏈傳動仿真模型的主要參數
為了便于分析,設置主動輪每秒轉過一個齒間角,則主動輪轉速為ω1=360/z1=360/17=21.18deg/s,模擬得到鏈條速度曲線如圖4所示。
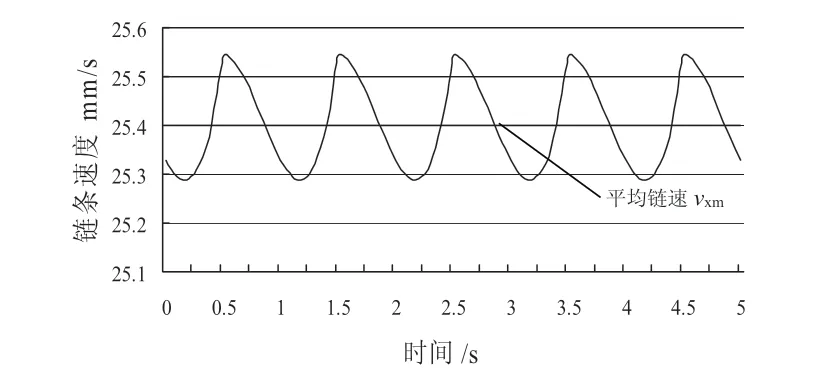
圖4 鏈條速度曲線
由圖4可知,在鏈傳動的過程中,鏈條速度不斷變化,最大速度vxmax=25.543mm/s,最小速度vxmin=25.288 mm/s;同時具有周期性,周期T=1s。經過計算鏈條的平均速度vxm= 25.3996mm/s。
圖5所示為從動鏈輪角速度曲線。由圖可知,從動鏈輪的轉動具有不均勻性,隨時間作周期性變化。最大角速度ω2max=10.3506deg/s,最小角速度ω2min=10.2424 deg/s,周期T=1s,平均角速度ω2m=10.2853deg/s。
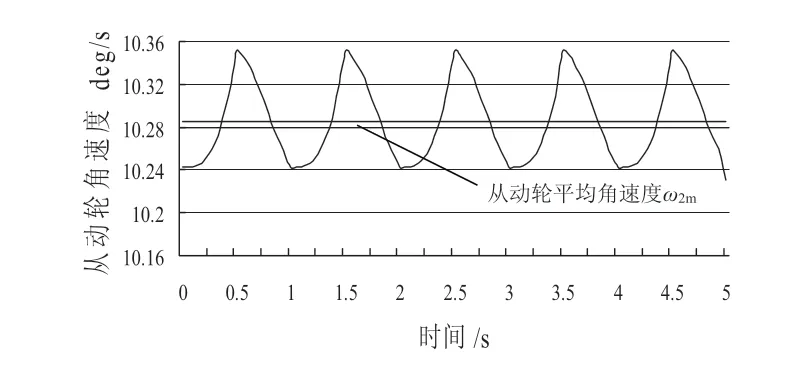
圖5 從動鏈輪角速度曲線
圖6 所示為瞬時傳動比is變化曲線。由圖可知,主動鏈輪雖等速轉動,但瞬時傳動比并非恒定,而是隨時間不斷作周期性變化。與平均傳動比i=ω1/ω2= z2/z1=35/17=2.0588相比,當從動鏈輪角速度最大時,瞬時傳動比最小;當從動鏈輪角速度最小時,瞬時傳動比最大。最大瞬時傳動比ismax=2.0675,最小瞬時傳動比ismin= 2.0459,變化周期T=1s。
圖6 瞬時傳動比is變化曲線
4 鏈速的影響因素分析
4.1 鏈輪齒數對鏈速的影響
在節距和轉速一定的情況下,分析鏈輪齒數對鏈速的影響。節距p=25.40mm,主動輪轉速為ω1=50deg/s,分別采用如下齒數的鏈輪:1)z1=5;2)z1=7;3)z1=11;4)z1=17;5)z1=21;6)z1=27; z1=31。
齒數不同,引起的鏈速變化幅度也不同。現引入鏈速的不均勻系數δ來計量鏈速的變化,δ等于:
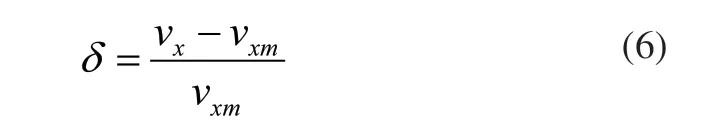
根據模擬結果,得到鏈速的不均勻系數曲線如圖7所示。各齒數對應的不均勻系數數值如表2所示。
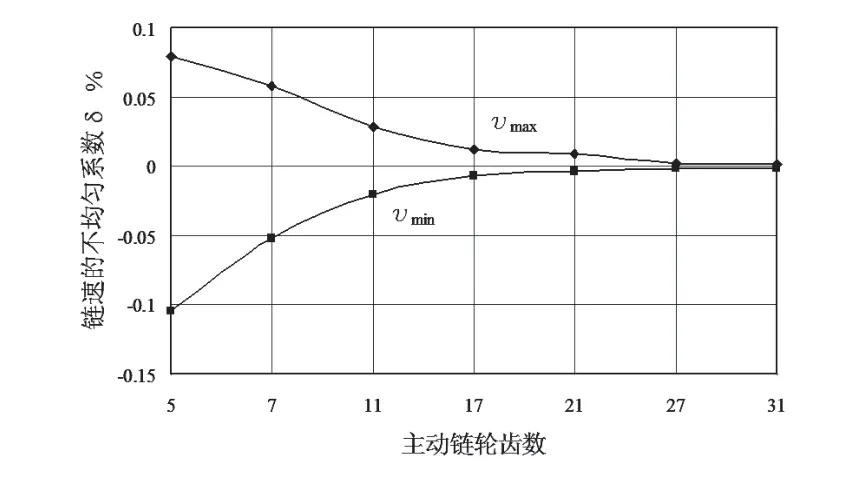
圖7 鏈速的不均勻系數曲線

表2 鏈速的不均勻系數數據表
由圖7可知,隨著齒數的增加,不均勻系數在變小,即鏈速的變化幅度在減小。z1≤17時,曲線陡峭,齒數變化對鏈速的不均勻性影響明顯;z1>17時,曲線趨于平緩,齒數變化對鏈速的不均勻性影響不明顯。
由表2可知,當齒數z1=5或7時,齒數少,鏈速變化幅度大,δmax和δmin均大于5%,鏈速非常不均勻,難以完成正常的傳動;當齒數z1=11或17時,鏈速的變化幅度明顯變小,但δmax或δmin大于1%,鏈速不均勻性仍較大;當齒數z1=21,27或31時,鏈速的變化幅度繼續變小,δmax和δmin均小于1%,不均勻性很小,能夠滿足大多數傳動要求。
4.2 鏈條節距對鏈速的影響
鏈輪齒數和轉速相同,分析節距對鏈速有影響。節距分別等于12.70mm,25.4mm,50.8mm,76.20mm,模擬得到的鏈條速度變化幅度曲線如圖8所示。
從圖8可以看出,節距不同,鏈速變化幅度就不同。這說明鏈速的變化大小與節距的大小有關,節距越小,鏈速變化越小,反之,節距越大,鏈速變化越大。同時,節距越大,鏈條向齒頂移動的距離越大。因此,節距越小,鏈速的不均勻性越小,鏈傳動的平穩性就越好。
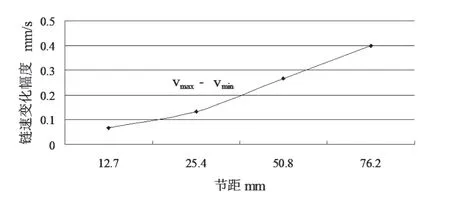
圖8 鏈條速度變化幅度曲線
5 結論
分析可知,在鏈傳動的過程中,鏈速、從動鏈輪角速度、瞬時傳動比均隨時間作周期性變化。鏈條速度受鏈輪齒數和鏈條節距的影響。齒數增加,鏈速不均勻性變小。節距越小,鏈速的不均勻性越小,鏈傳動的平穩性就越好。
通過數字樣機的仿真模擬,可以得到鏈傳動的各種運動變化曲線,也可以通過查詢模擬記錄列表,準確地找出某一時刻各項參數的具體數值。
與以往只是對鏈傳動的運動過程進行定性的理論計算分析相比,其仿真模擬分析更為直觀和詳細。該數字樣機可以代替鏈傳動機構的物理樣機,為設計和研究降低了成本和提高了效率。同時也為鏈傳動的優化設計及改善其運動學性能提供了一種可行的方法和手段。
[1] 榮長發.鏈傳動的振動和噪聲研究現狀與發展[J].機械傳動 2004,28(2):63-65.
[2] 楊剛.滾子鏈傳動系統動力學特性分析[J].工程力學,1996,13(3):22-26.
[3] 張經源. 鏈條傳動及制造[M].杭州:浙江大學出版社,1989.

