關于孤立導體在點電荷靜電場中的感應電荷分布情況探討

陜西寶雞中學 林嘉豪

1 引言

導體中存在著大量可以自由運動的電荷，稱為自由電荷。當孤立導體處于靜電場中時，自由電荷將在電場力的作用下發生移動并聚集在導體表面，這種現象稱之為靜電感應現象[1]。導體表面的感應電荷將在導體內部建立起與原靜電場方向相反、大小相等的電場，從而使得導體內部為等勢體，不存在任何電場分布，此時導體的狀態稱之為靜電平衡狀態[2]。對于靜電平衡態時導體表面的感應電荷分布情況，已經有一些理論推導和定性分析[3-7]。然而這些分析都沒有直觀的給出導體的感應電荷分布情況及其影響因素。本文通過有限元方法對點電荷靜電場中的孤立導體進行建模仿真，并定量分析其感應電荷的分布情況及其影響因素。

2 靜電感應現象理論基礎

通過查閱高等電磁理論可知，麥克斯韋方程組可以描述一切電磁場相關的物理規律，其中關于電場的高斯定理可以描述靜電場相關的現象。因而本文從電場的高斯定理出發，采用有限元方法建立二維模型對孤立金屬球在點電荷靜電場中的感應電荷分布情況進行了定量的數值仿真分析，相應的電勢分布及電場線如圖1所示。其中Q0表示源電荷的帶電量，D表示金屬球與源電荷的距離，R表示金屬球的半徑。以金屬球的球心為坐標原點，如圖1(a)建立坐標系（本文中均采用這一坐標系定義）。則當金屬球半徑R已知時，可以用.表示金屬球表面上任意一點。由圖1可見，將孤立金屬球導體放入點電荷產生的靜電場中，會顯著影響靜電場中的電勢即電場線分布，即是靜電感應的結果：1)金屬導體為等勢體，導體內部電勢處處相等；2）金屬導體內部沒有電場線，說明導體內部沒有電場分布；3）金屬導體附件的電場線被截斷，部分電場線從源電荷出發止于金屬導體表面，還有部分電場線從金屬球表面出發，說明金屬導體表面存在著感應電荷分布，根據電場線的方向可以進一步判斷出金屬球左右兩側感應出的電荷為異種電荷。下面將進一步具體分析這些感應電荷的分布情況及其影響因素。

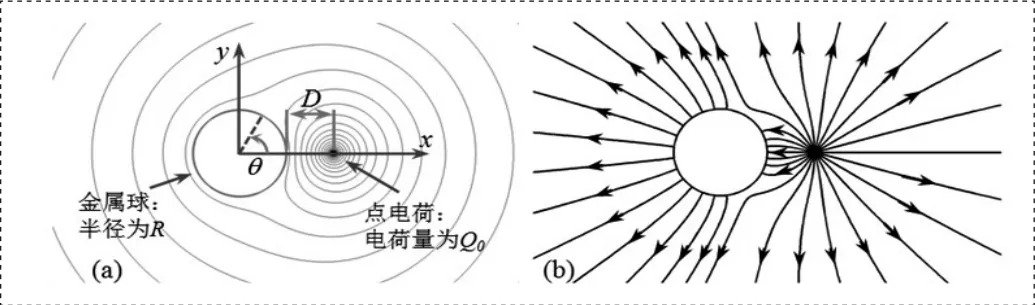
圖1

圖1 圓形導體在點電荷電場中的靜電感應現象：(a)等勢線；(b)電場線。其中Q0=10 C，R=10 cm，D=10 cm。

3 感應電荷分布的影響因素

由圖1(a)可知，上述靜電感應模型包括3個參數，即源電荷帶電量Q0，金屬球半徑R，金屬球與源電荷距離D。接下來逐一分析這幾個參數對感應電荷分布情況的影響。

通過有限元方法的數值仿真，我們可以得到金屬球表面上任意一點的感應電荷密度 。如圖1(a)所示，在金屬球表面靠近源電荷的區域會感應出異種電荷，在距離源電荷最近的點（）感應電荷的密度最大。而且隨著與源電荷距離的增加，感應電荷密度逐漸減小，直至為。此后隨著與源電荷距離的增加，感應電荷變為源電荷的同種電荷，而且電荷密度逐漸增大，直至距離最遠點時（）電荷密度最大。在R、D保持不變的情況下，進一步對比分析源電荷帶不同電荷量時的感應電荷分布：隨著源電荷帶電量的增加，金屬球上任意一點的感應電荷密度都會等比例的增加。即不同源電荷帶電量下 的分布曲線都完全重合，如圖所示。因此，在后續分析R、D對感應電荷分布的影響時采用歸一化感應電荷密度（）來表征以便排除源電荷帶電量對分析結果的影響。

圖2(b)所示的是在D=10 cm時分析R對感應電荷的影響。由圖可見，1）無論R如何變化，金屬球表面距離源電荷最近點（）的歸一化感應電荷密度都不變且為最大,原因在于這一點到源電荷的距離不隨R而變化且最近；2）隨著R的增加，距離源電荷最遠點（）的電荷密度逐漸減小；3）隨著R的增加，金屬球表面感應電荷密度為0的點對應的 向著遠離源電荷的方向移動。同理，可在R=10 cm時分析D對感應電荷的影響，如圖2（c）所示。隨著D的增加，金屬球表面距離源電荷最近點（）以及距離源電荷最遠點（）的歸一化感應電荷密度都會顯著減小；而金屬球表面感應電荷密度為0的點對應的也向著遠離源電荷的方向移動。

為了進一步分析其對金屬球總體感應電荷量的影響，我們對整個金屬球表面感應電荷密度進行積分求和，最終發現金屬球整體帶的電荷總量為0。說明靜電感應現象并沒有產生電荷，只是將金屬中的正負電荷分開了而已。為了分析被分開的電荷總量Q隨R、D的變化關系，我們將金屬球表面歸一化感應電荷密度為正的所有區域進行積分求和，可得歸一化總感應電荷量Q/Q0，如圖2(d(所示。歸一化總感應電荷量會隨著D的減小而顯著增加，隨著R的增加也會有所增加但增加量不夠顯著。這一現象說明金屬球歸一化總感應電荷量受R、D兩個參數的共同影響，但其中D對其的影響更為顯著。

圖2

4 結論

綜上所述，本文從麥克斯韋方程組中的電場高斯定理出發，利用有限元數值計算方法定量仿真分析了金屬球在點電荷靜電場中的感應電荷分布情況。當將孤立金屬球放置到點電荷附近時，在靜電場的作用下金屬球內部的正負電荷會分開，從而產生感應電荷。感應電荷僅分布著金屬導體表面，其靠近源電荷端感應出異種電荷且與源電荷距離最近點的感應電荷密度最大，同時遠離源電荷端會感應出源電荷的同種電荷且與源電荷距離最遠點的感應電荷密度最大。進一步分析發現：1）隨著源電荷帶電量的增加，金屬球上任意一點的感應電荷密度都會等比例的增加，即源電荷帶電量不會影響歸一化感應電荷密度的分布；2）金屬球的半徑R越大、金屬球與源電荷的距離D越小，相應的感應電荷量就會越多，而且其中D的影響更為顯著。上述的分析方法是從最基本的理論基礎出發，因而可以推廣到任意形狀孤立導體在任意源電荷電場中的靜電感應分析，具有廣泛的應用價值。

圖2歸一化感應電荷密度分布隨(a)源電荷帶電量、(b)金屬球半徑R、(c)源電荷距離D的變化關系的變化關系；(d)歸一化總感應電荷量（Q/Q0）隨金屬球半徑R、源電荷距離D的變化關系。

[1]趙升頻.導體在靜電場中的問題討論[J].重慶工學院學報(自然科學版),2007,21(11):91-93.

[2]朱炯名.導體的靜電平衡和感應電荷[J].物理教學,2011,33(2):5-8.

[3]胡成華.點電荷電場中金屬球面上的電荷分布[J].湖南城市學院學報(自然科學版),2005,11(2):47-49.

[4]江俊勤.關于靜電平衡中導體感應電荷分布的問題[J].物理教師,2001,22(11):29-30.

[5]楊浩忠.關于球形孤立導體在點電荷電場中產生的感應電荷的電量計算及分布[J].龍巖師專學報(自然科學版),1989,7(2):78-83.

[6]房淑芬.談靜電場中的導體[J].遼寧師專學報,2001,3(1):23-26.

[7]趙喚弟.用鏡像法求金屬球殼內外表面感應電荷的分布[J].松遼學刊(自然科學版),1989,1:64-66.