超低軌道衛星攝動特性分析及軌道維持方法*

溫生林，閆 野，易 騰

(國防科技大學航天科學與工程學院，湖南長沙 410073)

超低軌道是指飛行于大氣層以外而又低于一般航天器軌道高度的軌道，本文將超低軌道界定為軌道高度在120km以上、300km以下的飛行軌道。超低軌道飛行具有較大的經濟效益和工程應用價值，主要體現在:1)實現高分辨率對地偵察。對已有偵察載荷而言，選擇更低的軌道，可有效提高地面圖像分辨率，獲取更好的觀測效果。2)有效降低發射成本。在相同運載能力情況下，采用的軌道更低，超低軌道衛星的載荷能力更強，其效費比將比傳統航天器顯著提高。由于軌道高度低，超低軌道衛星的飛行環境和傳統衛星有很大不同，稀薄大氣和地球非球形攝動對軌道的影響顯著，且大氣密度隨晝夜、季節、太陽活動變化劇烈，超低軌道衛星受到的氣動力比傳統低軌衛星要高出兩到三個數量級［1］。盡管超低軌道上的大氣密度為10-11～10-9kg/m3的量級，作用在衛星上產生的氣動力能夠達到幾十毫牛的量級［2］，但長期積累，對衛星軌道的干擾影響巨大，若不進行軌道維持，衛星軌道會迅速衰減，因此，已有的飛行計劃都選擇避開這一空間區域，研究超低軌道維持的控制技術對于實現長時間的超低軌道飛行意義重大。

超低軌道飛行技術受到了美國、日本、歐空局等航天大國和著名研究機構的重視。當前，世界上已經發射和在研的真正實施超低軌道飛行計劃的衛星有三顆:歐空局的GOCE衛星［3］、日本宇宙航空研究局(JAXA)正在開發的SLAST衛星［4］以及美國Microcosm公司的NanoEye衛星［5］。歐空局于2009年3月發射的GOCE衛星是第一顆真正意義上的超低軌道衛星。GOCE衛星重約1t，采用細長體構型，發射高度為275km，在軌運行高度為250～260km，實際在軌飛行時間超過3年。SLAST衛星的飛行高度為180km，搭載離子引擎，以維持高度，飛行時間為半年，配備小型攝影機，衛星用很少的電力就能獲得很高的圖像解析度，實施高清晰度全天候監控。NanoEye是美國Microcosm公司正在研發的一顆對地觀測衛星，其軌道采用超低近圓軌道，近地點高度200km、遠地點高度300km，預計飛行時間為6個月～1年。NanoEye衛星是一顆低成本、高分辨率的成像偵察衛星，其凈重約20．6kg，可攜帶數倍于自身重量的推進劑，因而具有較好的機動性，使其在更低的軌道上(如160km)執行偵察任務。

目前，已有一些學者針對超低軌道衛星軌道保持問題展開了研究。文獻［6］引入僅受地球引力作用的虛擬衛星作為參考衛星，采用標準的線性二次調節器把低軌衛星軌道控制問題當成是衛星編隊來進行優化，該方法需事先對大氣阻力攝動進行預估。文獻［7］采用高精度加速度計測量衛星受到的非保守力，采用內嵌模型估計衛星的狀態與干擾，研究了利用內嵌模型實現GOCE衛星無阻力姿態與軌道控制的方法，該方法需要有高精度的姿態測量與穩定控制。文獻［8］給出了超低凍結軌道的概念，研究了利用常值小推力進行超低軌道維持的控制方案，這種控制策略是常值小推力以軌道周期為單位間歇工作，該控制方案在劇烈變化的強大氣阻力攝動作用下，將不能有效實現超低軌道高度的維持。

本文以飛行在軌道高度為120～300km超低軌道衛星的軌道維持問題為研究對象，由于受到強大氣攝動連續耗散力的作用，軌道長半軸將不斷衰減［9］，并面臨著大氣攝動隨太陽活動、季節變化、光照條件變化而不確定波動的難題，軌道控制方案與傳統的基于軌道根數的控制方法有很大不同［10-11］。考慮到進行軌道控制時，軌道偏心率會發生變化，為此，分析了在地球非球形引力攝動和大氣阻力攝動作用下偏心率的變化特性。在此基礎上，基于能量守恒原理提出了超低軌道維持的速度脈沖控制策略，對超低軌道維持的仿真結果表明，所設計的控制方案在實現軌道高度維持的同時，也將使得平均軌道偏心率矢量收斂至平衡位置，且用于軌道維持的燃料消耗合理，能夠滿足長時間的超低軌道飛行要求。

1 超低軌道偏心率變化分析

1．1 J2、J3項作用下軌道偏心率的變化特性

考慮地球引力J2、J3攝動項，偏心率和近地點幅角的長期變化率為［12］

式(1)中:a、e、ω和i分別為軌道長半軸、偏心率、近地點幅角和軌道傾角，p=a(1-e2);n為軌道平均角速度;RE為地球半徑;J2和J3分別為地球引力二階和三階帶諧項系數，ε的表達式如下

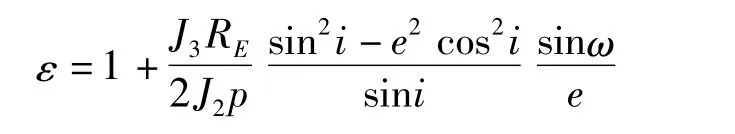
偏心率矢量定義為

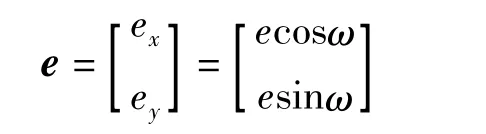
偏心率矢量大小為偏心率，方向由地心指向軌道近地點，偏心率矢量隨時間的變化可由以下微分方程描述:

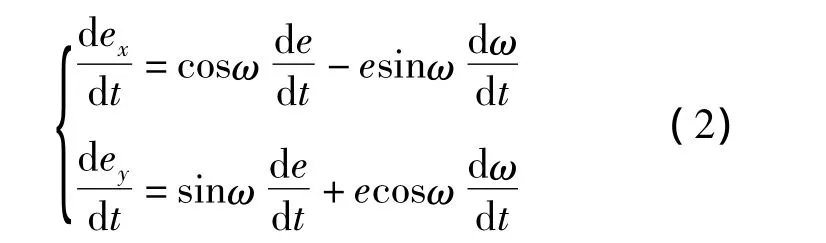
利用式(1)，保留e的一階項，可得

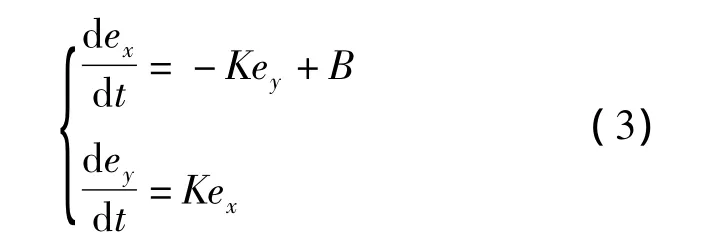
式(3)中:

由式(3)可得

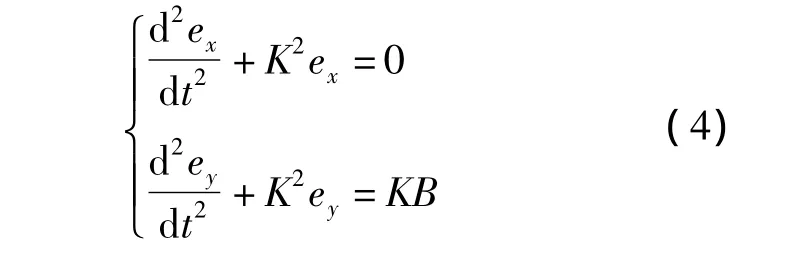
給定初始偏心率e0和近地點幅角ω0，對式(4)積分，可得

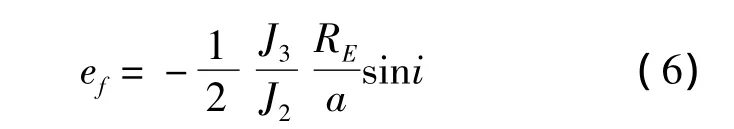
另一方面，根據式(4)，可得

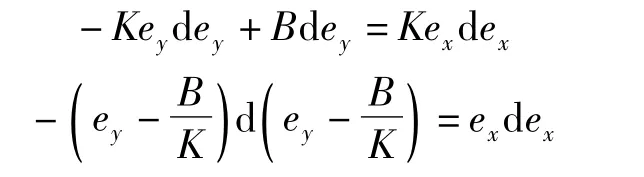
對上式積分，有

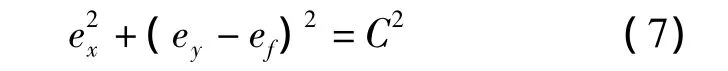
綜合以上分析，在J2、J3攝動項作用下，偏心率矢量的運動軌跡是以(0，ef)為圓心，C為半徑的圓，偏心率矢量的旋轉角速度為K。

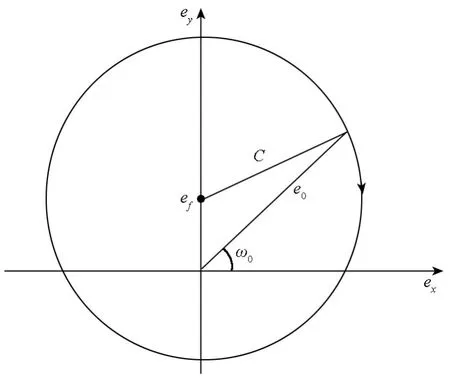
圖1 J2、J3攝動作用下平均偏心率矢量示意圖Fig．1 Average eccentricity vector sketch caused by J2，J3 zonal terms

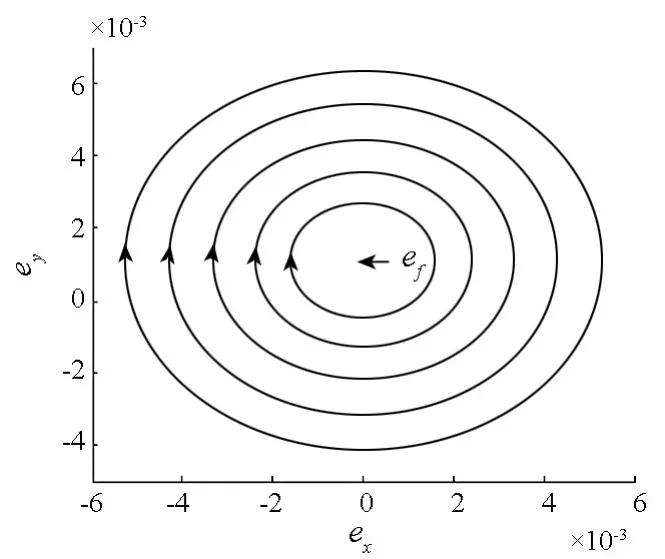
圖2 J2、J3攝動作用下平均偏心率矢量變化的仿真Fig．2 Average eccentricity vector simulation curve caused by J2，J3 zonal terms

初始時刻衛星的平均軌道根數為a=6558．137km，i=90°，Ω =0°，ω =90°，f=-90°。計算可知:ef=0．001 137，偏心率矢量旋轉角速度K=-9．13 ×10-7rad·s-1，(負號表示順時針旋轉)，旋轉周期為79．65d。在J2、J3攝動作用下初始偏心率取不同值時偏心率矢量的變化如圖2所示。由圖2可知，偏心率矢量的運動軌跡是以ef為圓心且過初始偏心率的圓。

1．2 大氣阻力作用下偏心率及近地點幅角的變化

超低軌道上的大氣密度隨太陽活動、季節、地磁場、光照條件等因素劇烈變化，在一個軌道周期內，可將大氣密度ρ表示成偏近點角E的函數ρ(E)。假設大氣阻力引起的軌道衰減可由軌道控制進行補償，在大氣阻力攝動作用下偏心率和近地點幅角的運動方程為［13］

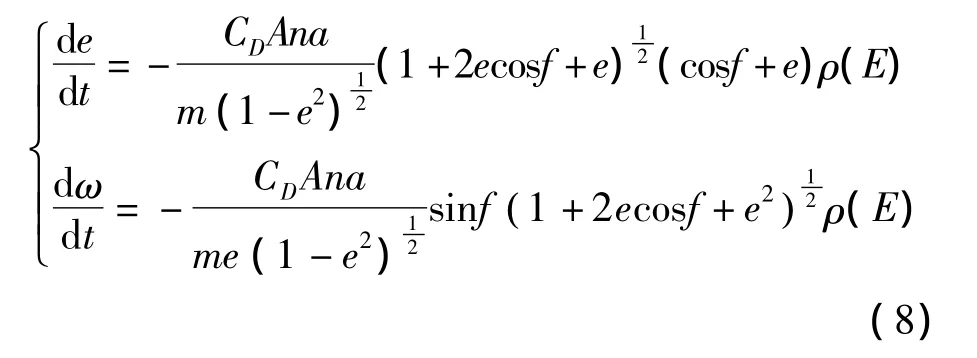
式(8)中:f為軌道真近點角，CD為阻力系數，A為迎風面積，m為衛星的質量。

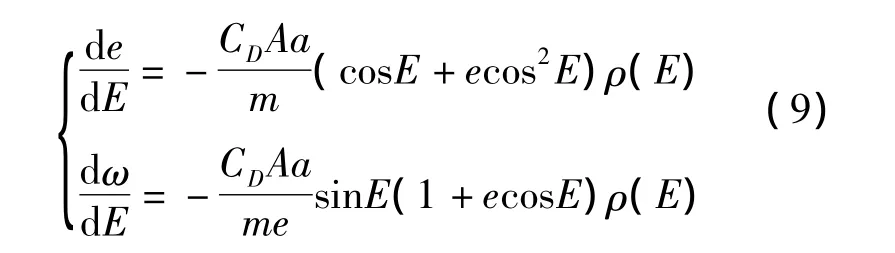
在大氣阻力作用下，偏心率的平均變化率為

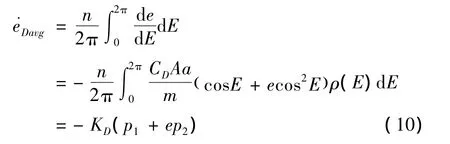
其中:

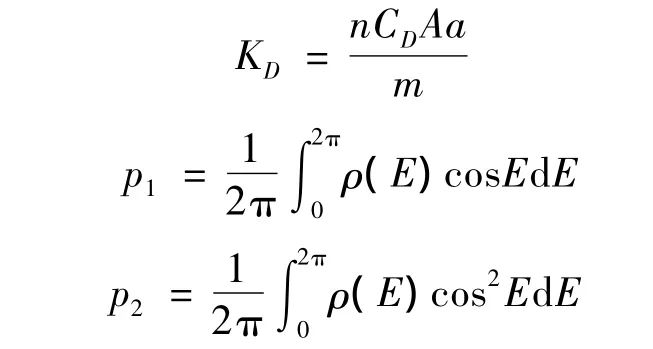
近地點幅角的平均變化率為

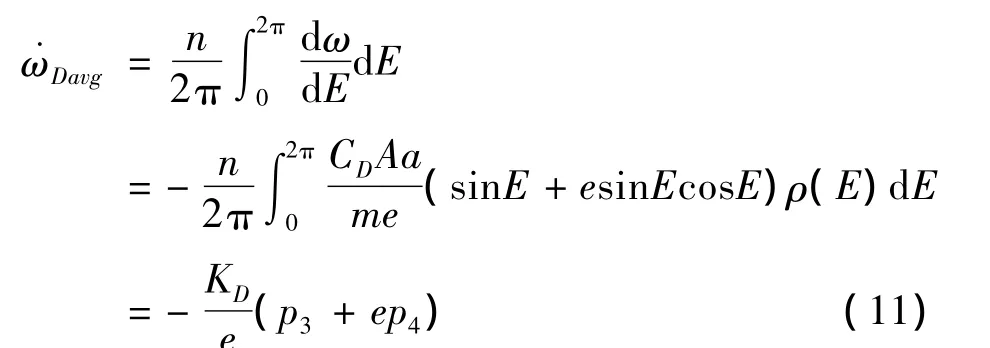
其中:

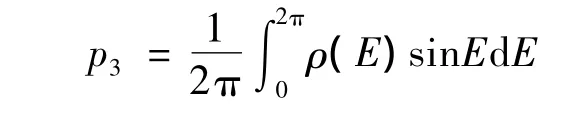
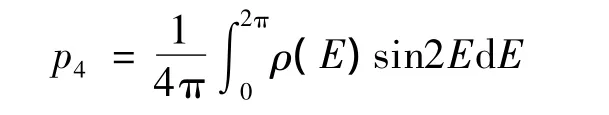
1．3 超低軌道偏心率矢量穩定性分析

結合式(1)、式(10)和式(11)，在 J2、J3引力攝動和大氣阻力攝動作用下，忽略O(e)項，偏心率和近地點幅角的平均變化率為

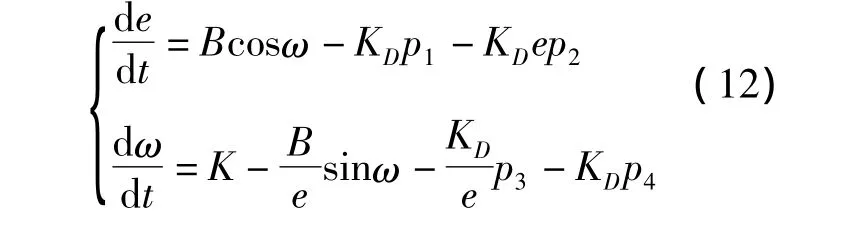
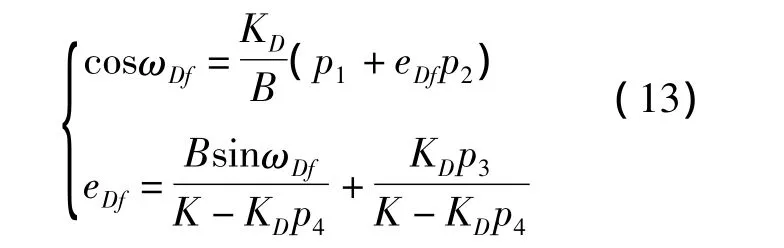
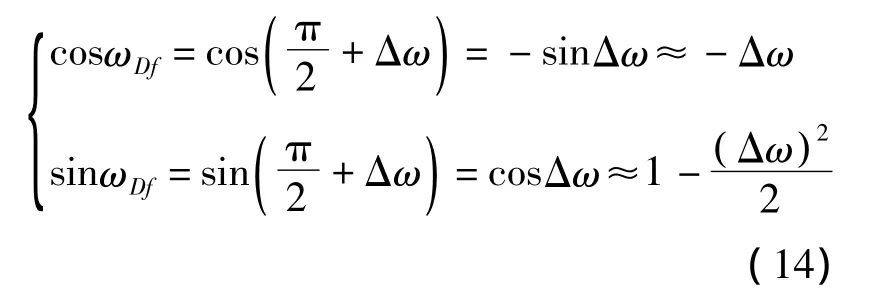
將式(14)代入式(13)，可得

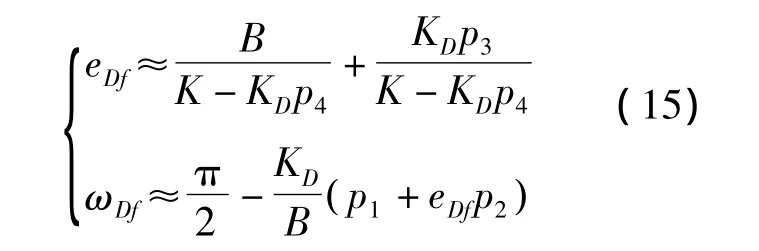
式(15)給出了在地球引力和大氣阻力作用下凍結軌道偏心率和近地點幅角的表達式，當當超低凍結軌道偏心率矢量可能的取值區域如圖3所示。

下面進行超低凍結軌道偏心率穩定性的分析，由式(14)可得偏心率和近地點幅角的雅可比矩陣在凍結軌道偏心率處的取值為

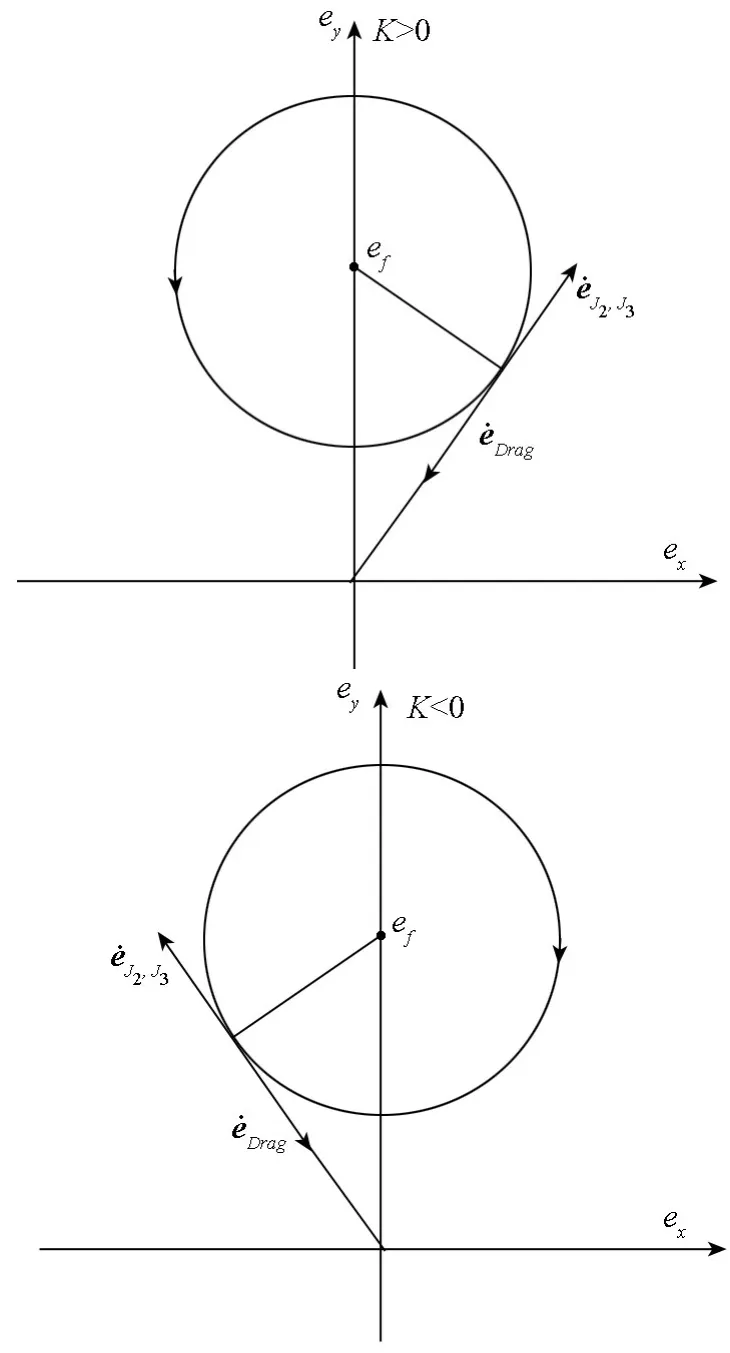
圖3 超低凍結軌道偏心率矢量的可能區域Fig．3 Possible region of super low altitude frozen eccentricity vector

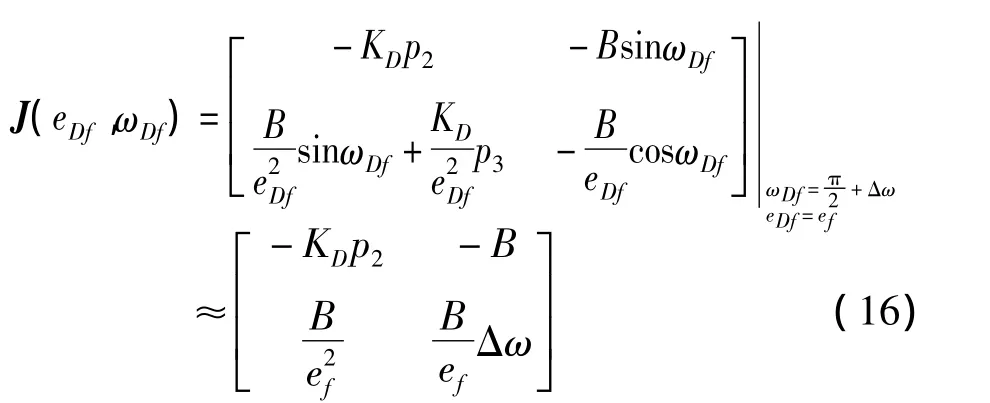
偏心率和近地點幅角的特征方程為

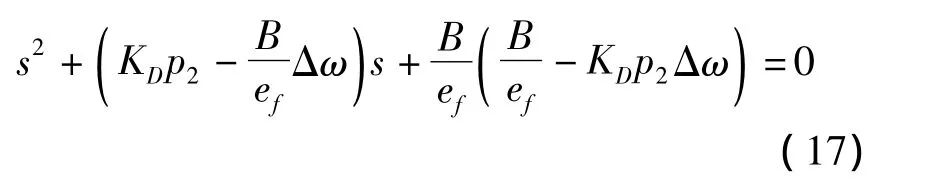
特征方程的根為

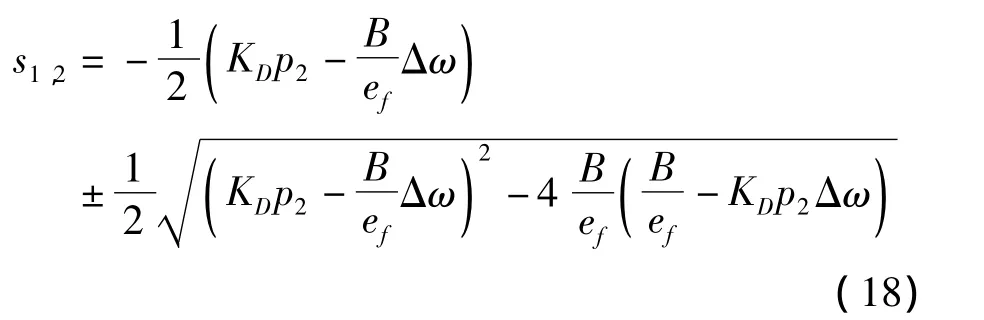
特征根的實部

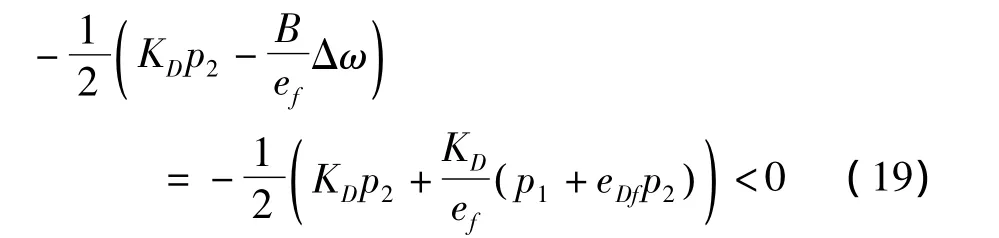
考慮到特征根的實部小于零，所以超低凍結軌道偏心率的變化是穩定的。當不考慮大氣密度、大氣密度為常值和余弦函數模型時，凍結軌道偏心率eDf、凍結軌道近地點幅角ωDf以及特征根的計算結果如表1所示。

表1 超低凍結軌道偏心率與特征根Tab．1 Eccentricity and roots of super low altitude frozen orbit

表1中:

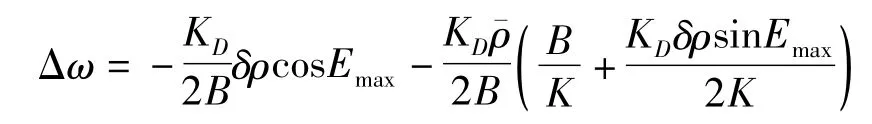
需要說明的是:上述結論是在僅考慮了地球引力和大氣阻力的影響，且認為軌道長半軸保持不變的假設下做出的。事實上，若在飛行過程中施加控制力，則軌道偏心率矢量的變化是復雜的。以上分析過程表明:在大氣阻力攝動作用下，軌道偏心率會變小，大氣阻力起到恢復力的作用。因此，在實施超低軌道高度維持的軌道控制時，可以不考慮軌道控制引起的軌道形狀的改變。

2 基于能量守恒原理的超低軌道維持方法

地球引力是保守力，在地球引力場中，衛星在軌運行僅存在動能和勢能的相互轉化，其機械能是守恒的，即動能與勢能之和是常量。單位質量的機械能ξ可表示為

式(20)中:U為地球的引力位函數。

計算引力位函數U時考慮中心引力、J2項以及J3項攝動，將更高階非球形引力攝動項當作擾動位函數進行處理，其表達式為

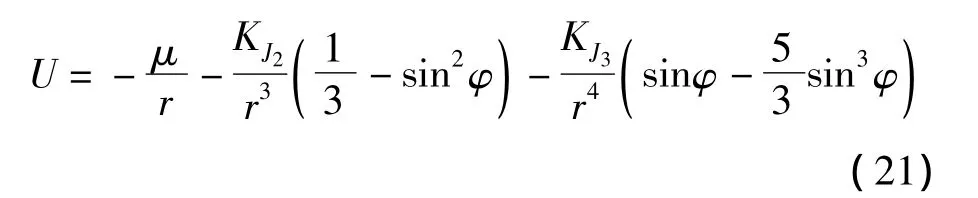
大氣阻力和控制力是非保守力，在地球引力、大氣阻力和控制力共同作用下機械能變化率的計算公式為

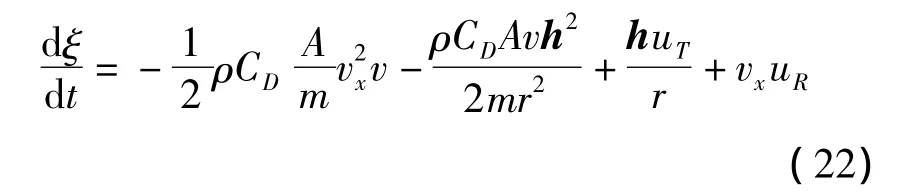
式(22)中:h為動量矩，r為地心距，vx為速度在軌道坐標系徑向分量，uT和uR分別表示控制加速度在軌道坐標系的徑向和橫向分量。

若僅在橫向施加控制加速度uT(t)，則可表示為

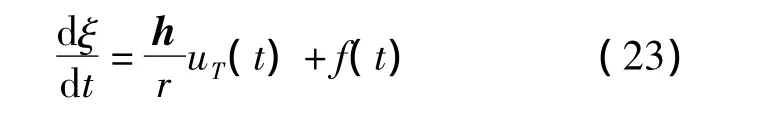
根據式(23)可知，進行超低軌道維持所需的速度脈沖ΔvT為

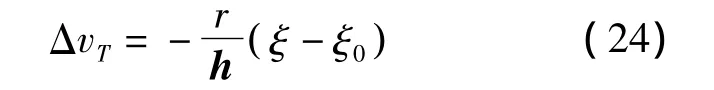
式(24)中:ξ0為初始時刻超低軌道衛星單位質量的機械能。

3 仿真分析

本文以軌道高度為200km的超低軌道衛星為例進行仿真和分析。初始時刻衛星的平均軌道根數為 a=6578．137km，i=45°，Ω =0°，f=0°，大氣阻力系數CD=2．2，衛星質量為500kg，面質比為0．02，軌道計算考慮了2階、3階引力場模型和大氣阻力攝動，大氣密度采用Harris-Priester大氣模型進行計算，仿真時間為50d。

在一個軌道周期內，分別在真近點角f0和f0+π處施加兩次速度脈沖進行軌道衰減補償控制，所需的速度脈沖由式(21)計算得到。

3.1 軌道高度維持的仿真結果

初始時刻平均偏心率為零，超低軌道高度維持的仿真結果如圖4、圖5所示。圖4和圖5分別給出了衛星的平均軌道高度和機械能在一天內的變化情況，圖中的虛線分別代表了初始時刻的平均軌道高度和單位質量的機械能，可以看出，其軌道高度和單位質量的機械能均始終在初始值附近變化。由圖5可以看出，在半個軌道周期內，大氣阻力可使軌道降低約1．2km。圖6給出了進行軌道衰減補償控制所需的速度脈沖在一天內的變化情況。

圖4 軌道高度變化曲線Fig．4 Curve of altitude change

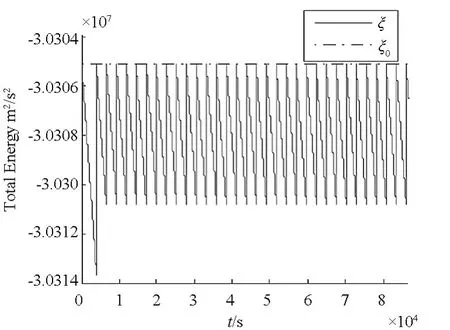
圖5 機械能變化曲線Fig．5 Curve ofmechanical energy change

表2給出了在整個軌道維持時間內平均軌道高度偏差、機械能偏差以及速度脈沖的統計結果。可以看出，采用速度脈沖的軌道維持策略時軌道高度偏差不超過-1871．2m，軌道高度偏差的平均值為-626．5m;軌道維持所需的速度脈沖最大值為 1．099m/s，平均值為 0．734m/s。在整個軌道維持時間內，所需總的速度脈沖為1247．7m/s，若發動機比沖 Isp=300s，則軌道維持所消耗的燃料質量為172．9kg，用于軌道維持的燃料消耗量占衛星總質量的34．6%，這表明:超低軌道維持的控制策略設計合理，能夠滿足長時間超低軌道飛行的要求。

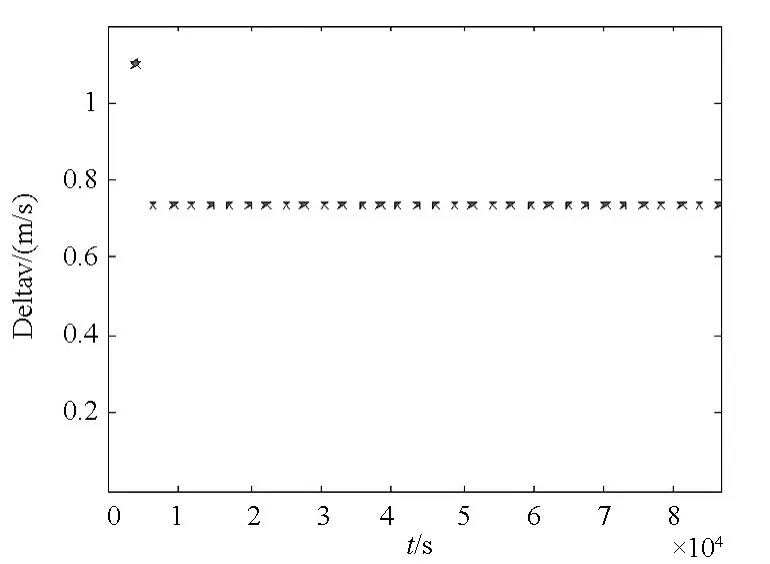
圖6 軌道維持所需的速度脈沖Fig．6 Velocity increment for orbitmaintenance

3.2 偏心率矢量的變化仿真

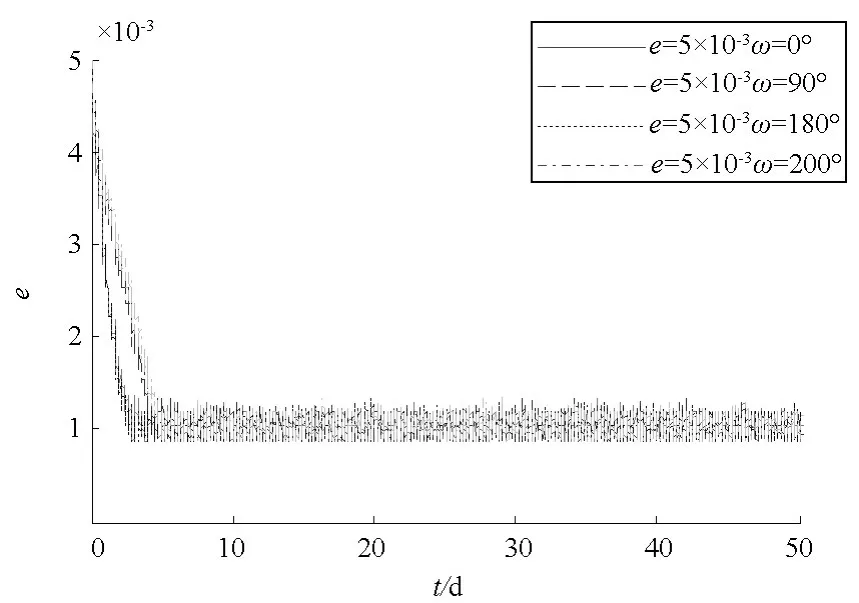
圖7 平均偏心率變化曲線Fig．7 Changes of average eccentricity

初始平均偏心率為0．005，初始近地點幅角分別取 0°、90°、180°以及270°時偏心率和偏心率矢量的仿真結果見圖7。圖7給出了偏心率的變化曲線，由圖7可得:平均偏心率在5d內從初值0．005 收斂至穩定值 0．001，隨后在 0．001 附近保持小幅震蕩。圖8給出了偏心率矢量的變化曲線，由圖7可得:雖然初始偏心率矢量不同，偏心率矢量都可以收斂至穩定位置，其中:初始近地點幅角取0°和270°時，偏心率矢量最終穩定在［0，0．001］附近;初始近地點幅角取90°和180°時，偏心率矢量最終穩定在［-0．001，0］附近。結合圖7和圖8可知:在地球非球形引力攝動、大氣阻力攝動和速度脈沖作用下，偏心率矢量從不同的初始值均可以收斂至原點附近的平衡位置，平衡位置取決于大氣阻力、控制力以及偏心率矢量初始值等多種因素。

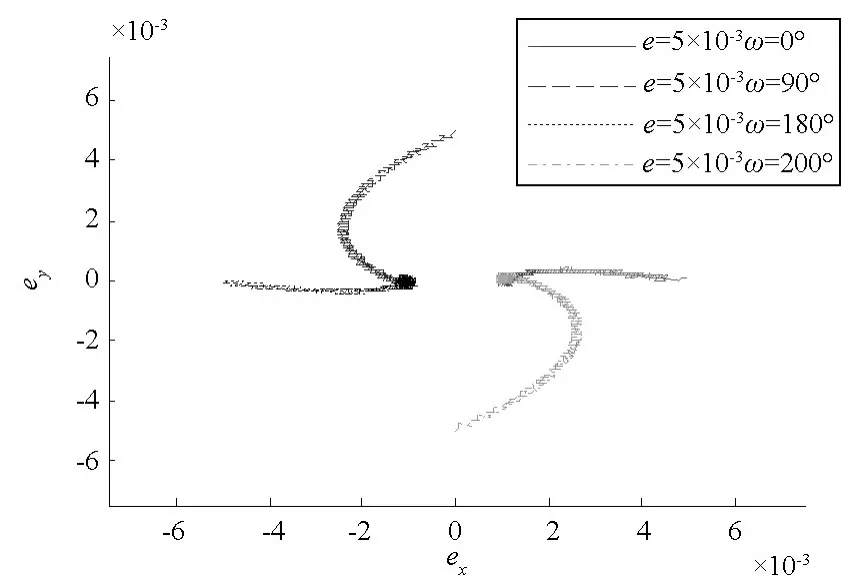
圖8 偏心率矢量變化曲線Fig．8 Curve of average eccentricity vector change

4 結論

本文研究了超低軌道衛星的軌道自主維持方法，分析了超低軌道衛星在地球非球形引力攝動、大氣阻力攝動作用下偏心率矢量的變化特性，提出了基于能量守恒原理的超低軌道維持策略。最后，以軌道高度為200km、質量為500kg的超低軌道衛星為例進行了仿真分析，主要結論有:

1)若不進行軌道維持，在半個軌道周期內大氣阻力可使軌道衰減約1．2km;在一個軌道周期內施加兩次速度脈沖進行軌道衰減的補償控制，在整個在軌飛行時間內，軌道高度偏差的平均值為-626．5m，軌道高度偏差不超過-1871．2m。

2)初始偏心率矢量不同，在地球引力、大氣阻力和速度脈沖共同作用下，偏心率矢量最終將收斂至原點附近。

3)在軌飛行 50d，所需總的速度脈沖為1247．7m/s，軌道維持所消耗的燃料質量為172．9kg，用于軌道維持的燃料消耗量占衛星總質量的34．6%，這表明:超低軌道維持的控制策略設計合理，能夠滿足長時間超低軌道飛行要求。

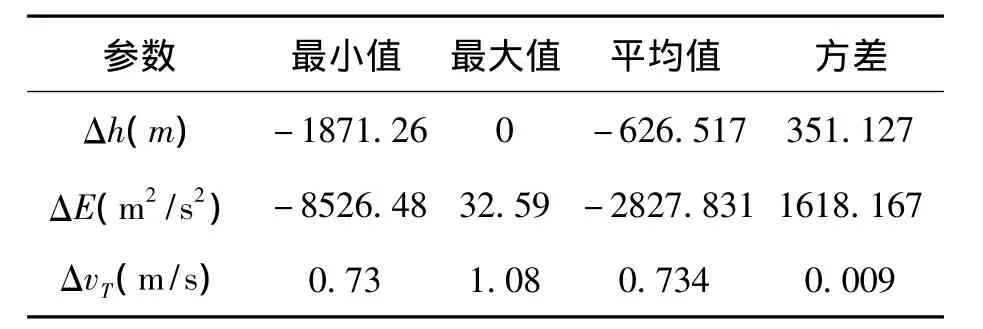
表2 軌道維持時主要控制參數統計Tab．2 Main control parameter statistics of orbitmaintenance

References)

［1］ Krueger J K． Closesat:perigee-lowering techniques and preliminary design for a small optical imaging satellite operating in very low earth orbit［D］．Cambridge:Massachusetts Institute of Technology，2010．

［2］ 周偉勇，張育林，劉昆．超低軌航天器氣動力分析與減阻設計［J］．宇航學報，2010，31(2):342-348．ZHOU Weiyong，ZHANG Yulin，LIU Kun．Aerodynamics analysis and reduced drag design for the lower LEO spacecraft［J］．Journal of Astronautics，2010，31(2):342-348．(in Chinese)

［3］ Kuijper D，Matatoros M A G．Goce flight dynamics operations from an orbital perspective［J］． Journal of Aerospace Engineering，Sciences and Applications，2012，2(4):93-106．

［4］ Atsushi N，Masanori H，Masayoshi U．The study of a super low altitude satellite［C］．58th International Astronautical Congress，2007，IAC-07-D1．4．06．

［5］ Van Allen，Richard E，James RW．NanoEye-amulti-mission low cost spacecraft［C］．Reinventing Space Conference，Los Angeles，CA，May 7-11，2012．

［6］ De Florio S，D'Amico S．Optimal autonomous orbit control of remote sensing spacecraft［C］//Proceedings of the 19th AAS/AIAA Space Flight Mechanics Meeting，Savannah，USA，2009:8-12．

［7］ Canuto E． Drag-free and attitude control for the GOCE satellite［J］．Automatica，2008，44(7):1766-1780．

［8］ Masayoshi U，Atsushi N．Orbital maintenance of super low altitude satellite by new frozen orbit［C］．The Meeting on the Study of Space Missions Propelled by Low-Thrust and Sustained Acceleration，Tokyo，Japan，Feb 28-29，2008．

［9］ Salama O．Autonomous orbit maintenance law for LEO sun synchronous，earth repeating satelliteswith electric propulsion system［C］．AIAA/AAS Astrodynamics Specialist Conference and Exhibit，Honolulu，Hawaii，USA，August18-21，2008．

［10］ Fearn D G．Economical remote sensing from a low altitude with continuous drag compensation［J］．Acta Astronautica，2005，56(5):555-572．

［11］ Florio S D．Precise autonomous orbit control in low earth orbit:from design to flight validation［D］．Glasgow:University of Glasgow，2013．

［12］ 楊嘉墀．航天器軌道動力學與控制(上)［M］．北京:中國宇航出版社，2005:196-198．Yang Jiachi．Spacecraft orbital dynamic and control(Volume 1)［M］．Beijing:China Astronautic Publishing，2005:196-198．(in Chinese)

［13］ 劉林，胡松杰．航天動力學引論［M］．南京:南京大學出版社，2006:166-169．Liu Lin，Hu Songjie．An introduction to spacecraft orbital dynamic［M］．Nanjing:Nanjing University Press，2006:166-169．(in Chinese)