高重合度人字齒輪傳動動態性能優化設計*

趙 寧，秋朋園，劉貴立

(西北工業大學機電學院，陜西西安 710072)

人字齒輪傳動具有承載能力高、工作平穩性好、自平衡軸向力等優點，因此被廣泛應用于航空、航天、船舶等領域。國外先進直升機已將人字齒輪傳動應用于其主減速器，以實現大功率的“分扭-并車”傳動。

高重合度人字齒輪副在嚙合傳動過程中，同時參與嚙合的齒數至少有兩對，單對齒上承受的載荷較小。Sivakumar［1］等對高重合度齒輪與普通齒輪進行了試驗驗證，結果顯示高重合度齒輪無論在使用壽命、可靠性還是承載能力方面都具有較大的優勢。但高重合度齒輪對誤差激勵、剛度激勵及嚙合沖擊激勵也較為敏感，因此，在對人字齒輪進行高重合度設計的基礎上，綜合考慮齒輪傳動的動態性能，對人字齒輪副進行綜合性能優化就顯得尤為重要。

目前，國內外對齒輪傳動的靜態性能優化設計研究得較多，理論較為成熟，對于動態性能的優化設計則研究得較少。杜雪松、朱才朝等考慮齒輪副的時變嚙合剛度、嚙合阻尼及輪齒的綜合誤差［2］，建立了船用齒輪傳動系統的動力學模型，以齒輪的振動加速度和質量為目標函數對船用齒輪的齒數、螺旋角及變位系數進行了多目標動態優化。張慶偉等考慮時變嚙合剛度、嚙合誤差以及風速變化引起的外載荷波動，建立了風力發電機齒輪傳動系統的集中參數模型，以各構件的振動加速度和系統體積/質量為優化目標函數［3］，設計齒輪的齒數、模數、齒寬。Wusanpan［4］分析了斜齒輪的螺旋角、壓力角、齒頂高系數等對齒輪傳動重合度及動態應力的影響，以齒輪的幾何尺寸緊湊及動態應力最小為優化目標，對輪齒參數進行了設計。Reagor［5］分析了不同載荷作用下斜齒輪副的變形及齒輪傳動誤差，設計輪齒的齒廓修形量來優化齒輪副的傳動誤差。但目前為止，動態優化的研究對象多為斜齒輪，對人字齒輪的動態特性優化還鮮有相關的研究。

本文提出的人字齒輪動態特性的優化基于人字齒輪系統動力學的研究，國內外學者在齒輪系統動力學方面已經取得了很多成果，但對人字齒輪系統動力學的研究一般將人字齒輪簡化為直齒輪考慮，忽略兩端軸向力，且在建模過程中未全面考慮人字齒輪左右端斜齒輪之間的相互影響及輪齒的安裝及制造誤差等因素。大量研究指出，對斜齒圓柱齒輪進行齒廓修形和齒向修形可大大降低齒輪的扭轉振動，有效地改善齒輪傳動系統的動態性能，但目前對考慮修形的人字齒輪動力學分析還未有深入研究。因此，建立和完善人字齒輪齒輪傳動系統的動態優化設計的理論和方法，進一步提高齒輪傳動系統的綜合傳動性能水平有重要意義。

本文在對航空人字齒輪進行高重合度設計分析的前提下，基于拋物線修形人字齒輪副承載接觸分析技術，綜合考慮了時變嚙合剛度、誤差激勵和嚙合沖擊激勵等因素的影響，針對人字齒輪傳動中主動小齒輪軸向浮動安裝的特點，應用集中質量法建立了人字齒輪副彎-扭-軸耦合非線性動力學模型，考慮了人字齒輪軸向浮動和左右兩輪間相互作用對人字齒輪傳動性能的影響，求解得到了齒輪傳動系統的動態響應。針對傳統遺傳算法在解決該類復雜的工程問題時適應值計算費時的缺點，提出了一種具有適應值預測機制的遺傳算法(Fitness Approximation Genetic Algorithm，FAGA)，大大提高了優化的效率。基于動態特性的分析結果，采用改進的遺傳算法對人字齒輪傳動的重合度及動態性能進行了優化設計，優化所得結果是一個非劣解。最終在人字齒輪減振降噪試驗臺上對優化前后的人字齒輪進行了帶載試驗，對比了優化前后齒輪運轉中的噪音分貝值。

1 人字齒輪傳動高重合度設計分析

重合度越大，意味著同時參與嚙合的輪齒對數越多，對提高齒輪傳動的平穩性和承載能力有著重要意義。圓柱齒輪傳動的重合度計算公式可參考文獻［6］。齒頂高系數及螺旋角對重合度的影響比較顯著，增加齒頂高系數可以得到較大的端面重合度εα，但齒頂高系數的增加必然會導致齒頂厚的減小。

人字齒輪可以看作是由兩個旋向相反的斜齒輪構成，小齒輪采用浮動結構，可自相平衡傳動時產生軸向力，因此可以采用較大的螺旋角來增大齒輪傳動的軸向重合度 εβ，一般取 25°～40°之間。

變位系數對齒輪重合度有一定的影響，本文主要針對航空人字齒輪進行優化設計，考慮到航空用人字齒輪對結構緊湊性的要求，本文在設計過程中，對人字齒輪采用等變位齒輪傳動，小齒輪采用正變位，大齒輪采用負變位，在控制齒輪傳動系統幾何尺寸的同時提高齒輪傳動的承載能力。

2 人字齒輪傳動的動力學分析

機械系統的振動和噪聲大部分來源于齒輪傳動系統工作時產生的振動，齒輪系統的動力學行為對齒輪裝置的整體性能有著重要的影響。

2．1 齒輪系統動態激勵

系統輸入激勵的確定是進行系統動力學分析的先決條件，也是正確計算系統振動和噪聲的關鍵問題之一。

2．1．1 剛度激勵

一般情況，齒輪嚙合的重合度不是整數，因而，齒輪嚙合的綜合剛度是隨時間周期變化的。

本文將有限元法、柔度矩陣及非線性規劃等相結合，基于有限元綜合柔度矩陣的非線性規劃法，針對人字齒輪均載傳動的特點，建立了考慮拋物線修形的人字齒輪承載接觸仿真模型［7-12］，利用人字齒輪承載接觸分析，計算得到一個嚙合周期內不同嚙合位置的接觸力和接觸變形，從而得到該位置的嚙合剛度。將計算得到的嚙合剛度的離散值通過多項式擬合及Fourier級數變換轉化為周期函數的形式。航空人字齒輪由于其特殊應用，傳動較為平穩，計算得到的剛度激勵幅值較小。

2．1．2 誤差激勵

輪齒嚙合誤差是由輪齒加工誤差和安裝誤差引起的。本次人字齒輪的動力學建模過程中考慮齒輪嚙合輪齒間的齒形誤差及基節誤差。根據齒輪加工精度等級，通過查齒輪手冊相關誤差，從而合成系統的等效誤差。航空人字齒輪制造及安裝等級要求較高，系統等效誤差較小。

2．1．3 嚙合沖擊激勵

齒輪嚙合過程中，由于齒輪的誤差和受載彈性變形，使一對輪齒在進入及退出嚙合時，其嚙入點和嚙出點偏離嚙合線上的理論嚙合點，引起嚙合沖擊。由于輪齒嚙入沖擊的影響明顯大于嚙出沖擊，因此本文著重考慮嚙入沖擊激勵。根據齒輪嚙合原理和機械動力學理論，確定初始嚙合位置、沖擊速度及嚙入沖擊力，最終得到一個嚙合周期內人字齒輪副的嚙入沖擊激勵。

2．2 人字齒輪副嚙合耦合型振動模型

根據人字齒輪均載傳動的特點，大人字齒輪采用固定安裝，主動小輪采用軸向浮動安裝。建模過程中考慮了人字齒輪軸向浮動及人字齒輪左右兩輪間的相互影響作用［13］。其中傳動軸、軸承和箱體的支撐剛度和阻尼均用組合等效值代替。采用集中參數法建立了人字齒輪副彎-扭-軸耦合的振動分析模型如圖1所示。

不考慮齒面摩擦的影響，該系統為12自由度動力學模型，系統的廣義位移列陣{δ}可表示為，

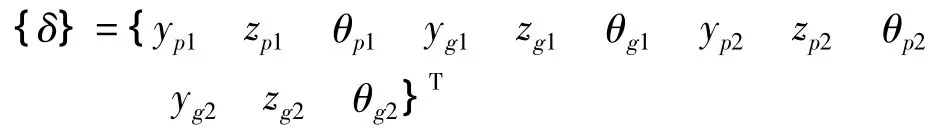
式中，yij，zij和)分別為主、從動人字齒輪左右端斜齒輪的中心點Op1，Op2和Og1，Og2在y向，z向的平移振動位移和轉角振動位移。

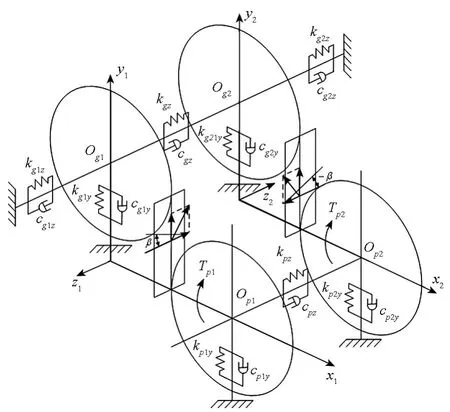
圖1 人字齒輪彎-扭-軸耦合的振動分析模型Fig．1 Bending-torsional-axial coupling dynamic model

圖 1 所示的模型中:kp1y，kp2y，kg1y，kg2y為組合等效支撐剛度;cp1y，cp2y，cg1y，cg2y為組合等效支撐阻尼;kg1z，kg2z為大齒輪的軸向支撐剛度;cg1z，cg2z為大齒輪的軸向支撐阻尼。kgz，kpz為大小齒輪軸的軸向拉伸(壓縮)剛度;cgz，cpz為軸的軸向拉伸(壓縮)剛度。

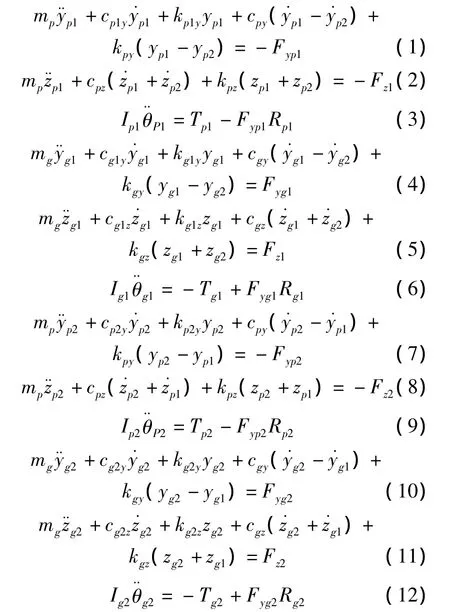
根據牛頓力學定律，圖1所示的人字齒輪傳動系統的運動微分方程為:式中:mp，mg，Ip1，Ip2，Ig1，Ig2分別為人字齒輪左右端小齒輪和大齒輪的質量及轉動慣量;Rp1，Rp2，Rg1，Rg2為人字齒輪左右端小齒輪和大齒輪的分度圓半徑;Fyp1，Fyp2，Fz1，Fyg1，Fyg2，Fz2分別為人字齒輪左右端斜齒輪的輪齒嚙合切向及軸向動態嚙合力。

將齒輪扭轉振動方程進行合并，定義量綱時間t=τωn，同時引入一個人為設定的位移標稱尺度bc，對上述人字齒輪運動微分方程進行無量綱化處理，可得系統的無量綱化運動微分方程如下所示。

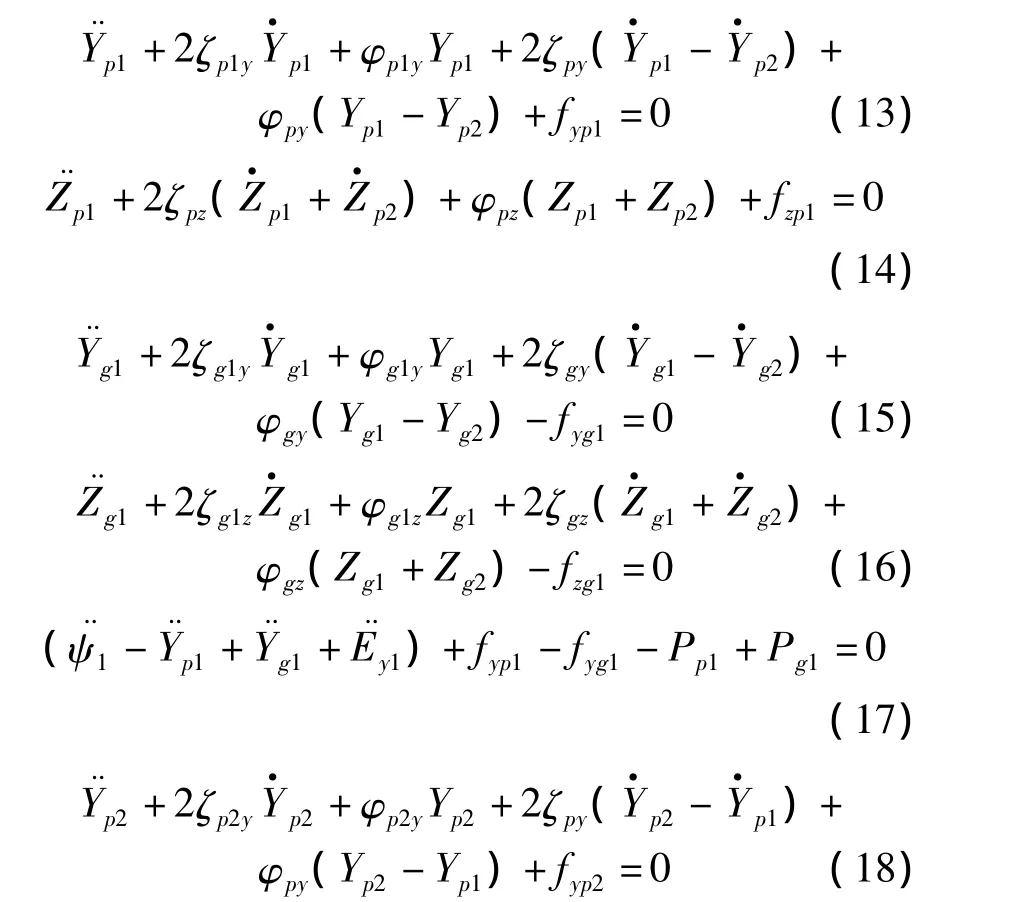
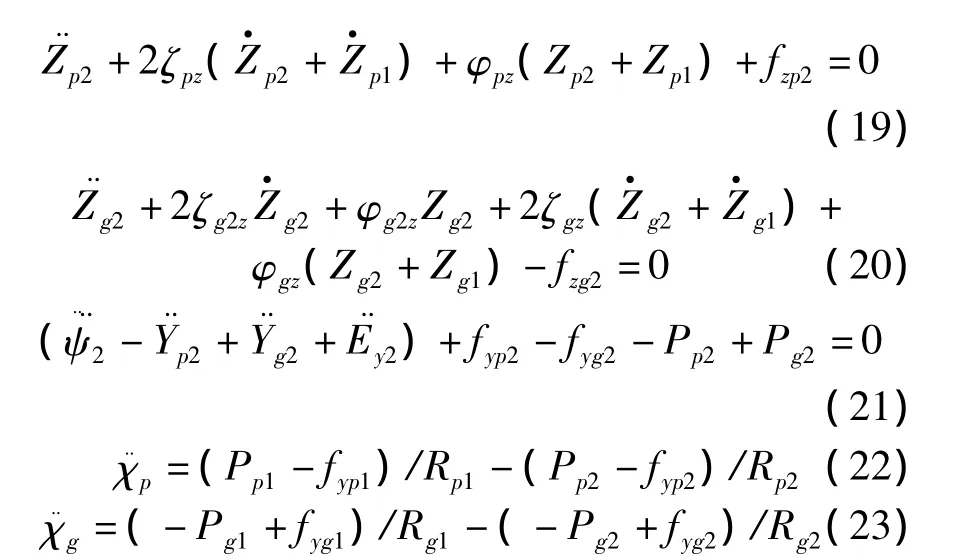
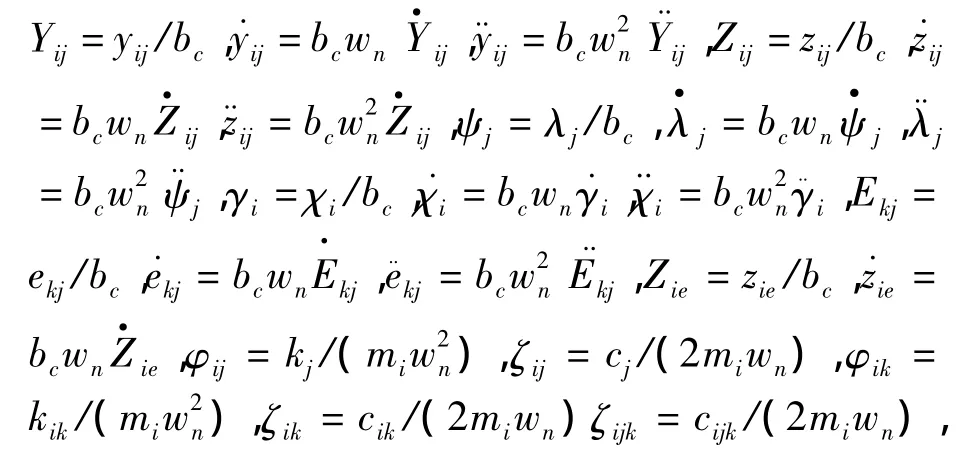
2．3 人字齒輪耦合振動模型求解

齒輪振動以輪齒的嚙合周期為周期，為了便于利用數值積分方法來求解運動微分方程，對運動微分方程組進行降階處理。本文采用MATLAB的ODE45數值方法進行求解，根據降階處理后的一階微分方程組，編寫計算導數的ODE函數文件，該方法采用的數值積分方法是四階～五階Runge-Kutta算法。

初始位移由平均負載下的系統靜態變形確定，初始速度由系統的理論轉速確定，這里將初始速度置“0”。靜變形的位移條件較接近穩態振動的彈性變形，速度初值置“0”，剔除了系統中的剛性轉動成分，只剩下振動分量，因此能較好地求解系統的穩態響應。

考慮初始計算值的不穩定性，將開始計算獲得的數百個周期的響應略去。為使得求解結果更為直觀，將計算得到的無量綱結果還原為實際的計算結果，求解獲得人字齒輪副在嚙合周期內的動態響應。

3 動態性能優化設計的數學模型

3．1 設計變量

設計變量的選取中，首先應考慮所選取的設計變量應對齒輪的動態性能影響較大;其次，結合本文第一節關于航空人字齒輪的高重合度設計的分析，考慮航空齒輪減重降噪的特殊要求。因此，本次優化設計中，采用增加齒頂高系數、增大螺旋角的方法來提高人字齒輪傳動總重合度εγ，同時采用等變位齒輪傳動，小齒輪采用正變位，大齒輪采用負變位，既控制了齒輪傳動系統的幾何尺寸，同時也提高了齒輪傳動的承載能力。

大量研究指出，剛度激勵和沖擊激勵是引起輪齒嚙合線方向振動的主要因素，對斜齒圓柱齒輪進行齒廓修形和齒向修形可大大降低齒輪的扭轉振動。在動力學分析中主要表現為對齒輪進行修形，改變了齒輪傳動過程中的嚙合剛度及沖擊激勵，從而有效地改善齒輪傳動系統的動態性能。

考慮到輪齒的修形是通過改變刀具切削刃的形狀實現的，刀具的拋物線齒廓易于加工，且試驗證明對漸開線圓柱齒輪采取拋物線形齒廓修形能有效改善齒輪嚙合性能［14-15］，因此，本文在齒廓修形設計中，齒條齒廓采用拋物線代替直線齒廓。齒條齒廓拋物線修形方程的表達式為:

A，B為齒條齒廓拋物線修形的二次項系數及常數項，即確定齒廓修形的修形程度及修形頂點。

為了改善工作狀態下的齒面載荷分布不均，齒向采用沿分度圓螺旋線方向的拋物線修形。齒向拋物線修形方程的表達式為:

C為人字齒輪齒向拋物線修形二次項系數，修形頂點齒向位于單側斜齒輪齒寬中點處。

同時考慮到設計制造的經濟性，將嚙合齒輪的變形量都集中反映在小齒輪上，僅對小齒輪進行齒廓及齒向的拋物線修形。實際加工中，若不采用改變刀具切削刃的形狀進行修形，只要將修形參數換算為相同的輪齒齒廓及齒向修形量，即可達到預期的效果［16-17］。綜上所述，本次優化設計所選擇的設計變量為:

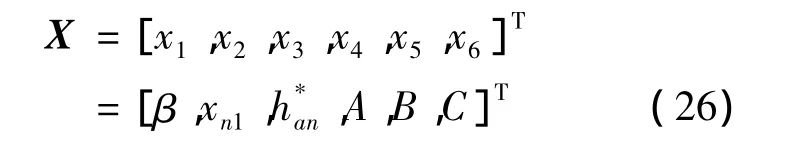
其中:β為螺旋角;xn1為法面變位系數;h*an為法面齒頂高系數。

3．2 目標函數

齒輪傳動系統的振動噪聲與振動加速度的均方根值成正比，它反映齒輪傳動系統的動態性能。研究表明齒輪副嚙合線上相對振動加速度和齒輪軸向振動加速度是引起齒輪振動噪聲的主要原因［17］。通過對人字齒輪動力學模型進行求解分析，可知人字齒輪左右兩端齒輪副的動態響應曲線具有相似的形式，計及人字齒輪的特殊結構及兩端齒輪副的相互影響，動態響應曲線僅有微弱的差別。本文采用人字齒輪左側齒輪在一個嚙合周期內齒輪沿嚙合線方向振動加速度的均方根值作為齒輪系統動態性能最優設計的目標函數:

3．3 約束條件

為了保證齒輪副傳動的連續性與平穩性，防止發生邊緣接觸時齒輪副運動的強振動性，對人字齒輪進行強度約束，膠合約束及滑動率約束等。同時，對最大動載荷、輪齒剛度變化幅值等動態性能指標均進行約束。將齒輪傳動的設計重合度放在約束條件中，保證優化過程中重合度提高。

3．4 優化方法

本次優化方案中，優化變量為齒輪副的設計參數，優化的目標函數為人字齒輪副傳動系統的動態響應求解結果，兩者之間無法直接建立解析表達式，且該優化問題在優化所得的解空間內存在多個局部最優解，因此傳統的優化算法對于此類問題的求解并不適用。

遺傳算法是一種借鑒生物界自然選擇和自然遺傳機制的人工智能型方法［18］。對于一些用傳統優化算法難以有效解決的問題，應用遺傳算法是一個卓有成效的新途徑。

由于本文優化的目標函數的計算過程復雜，包括人字齒輪承載接觸分析，非線性動力學微分方程的求解等，應用傳統的遺傳算法導致尋優過程中計算適應值極其耗時。因此，本文提出了一種具有適應值預測機制的遺傳算法(Fitness Approximation Genetic Algorithm，FAGA)。該算法包含一種基于可信度概念的適應值預測模型，可以根據預測的準確度自適應地調整預測的時機和頻率，在預測準確度和預測頻率之間反復博弈，最終獲得二者之間的平衡，從而在保證結果準確性的前提下，最大程度上減少真實適應值的計算次數，提高計算效率。

3．4．1 基于可信度的適應值預測模型

1)可信度及適應值共享半徑

對于種群中的每一個個體i，都有其對應的適應值fitness(i)以及該適應值的可信度R(i)。當fitness(i)是真實計算的適應值時，其可信度R(i)=1;當fitness(i)是預測的值時，其可信度0≤R(i)＜1。

如圖2所示，對于種群中的每一個個體i，指定其適應值共享半徑rshare，解空間中到個體i的無量綱歐氏距離不大于適應值共享半徑rshare的區域稱作個體i的適應值共享區域，記作Ωi。

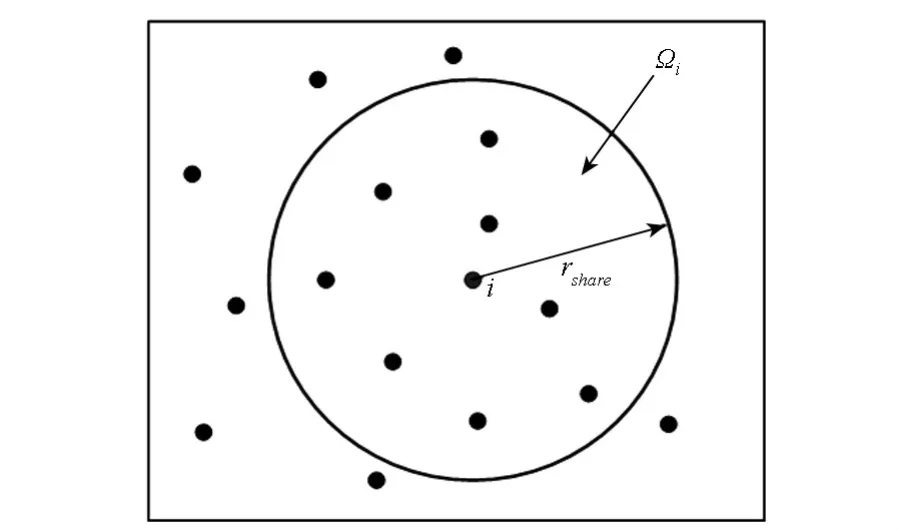
圖2 適應值共享區域Fig．2 Shared region of fitness

本文在計算中采用一種自適應的適應值共享半徑計算方法，具體公式參考文獻［19］。

2)適應值計算方法

假設個體i的適應值共享區域Ωi中包含m個其他個體，這m個個體組成集合S={s1，s2，…，sm}。則個體i的適應值fitness(i)計算方法如下:

首先按式(28)計算個體 i的預測可信度R(i)。

式中:sj表示Ωi中包含的一個個體，R(sj)表示sj的可信度，ω(sj)表示sj對個體i可信度的貢獻權重。設集合S中每個個體到個體i的無量綱歐氏距離分別為ˉd1，ˉd2，…，ˉdm，則ω(sj)可由式(29)計算得到。

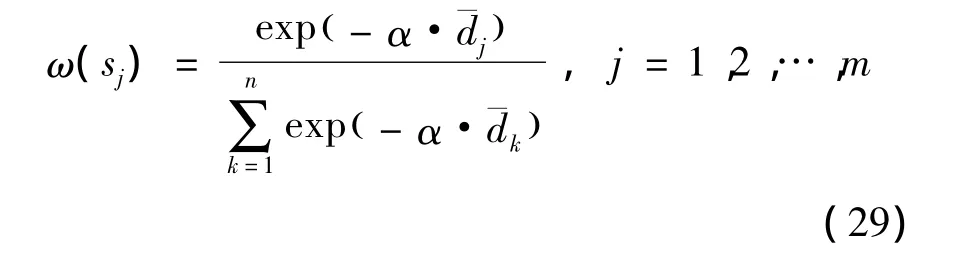
式中:α為權重放縮系數。

如圖3所示，判斷可信度R(i)是否超過信任閾值R*，若R(i)≥R*，則按照式(30)預測個體i的適應值;否則R(i)＜R*，計算個體i的真實適應值，并將其適應值可信度R(i)置為1。

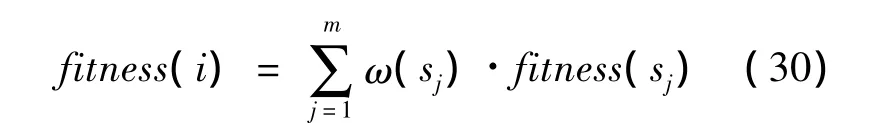
3)歷史種群更新及可信度流失

為了防止歷史種群信息的規模過于龐大而導致空間復雜度和計算量的增大，每一代進化完成后，需要剔除冗余的數據，因此引入種群個體冗余度的概念來判別數據是否冗余。數據庫中某個個體i的冗余度Ir定義為:

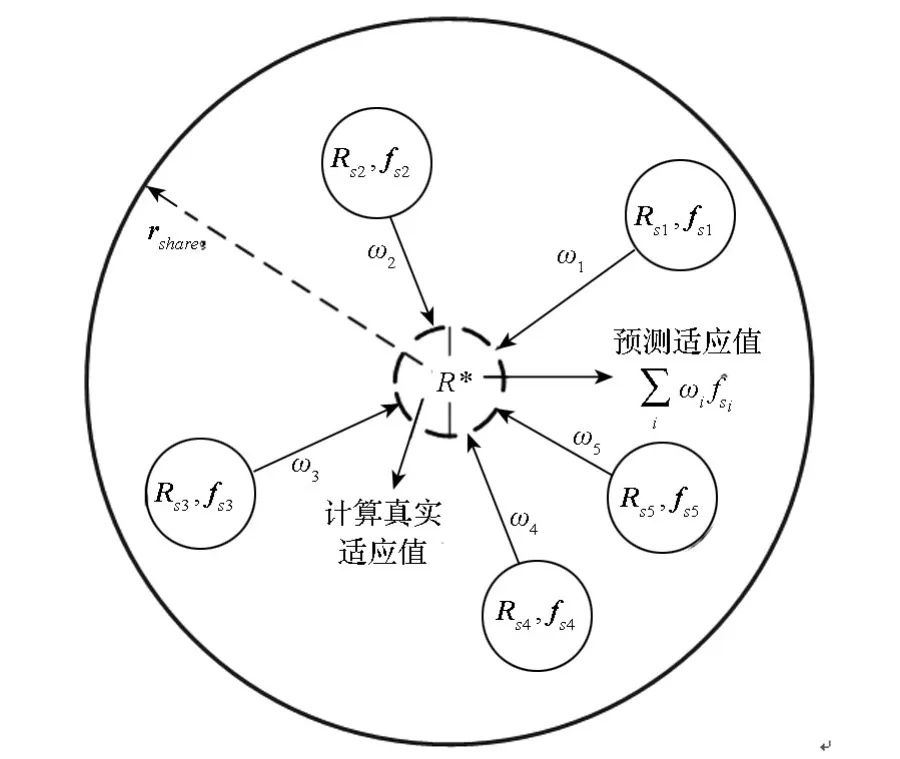
圖3 適應值預測模型Fig．3 Predictionmodel of fitness

式(31)中Δˉxk(i)表示在設計空間的第k維上，個體i的前一個投影點與后一個投影點的坐標差值(取絕對值)。當某個體的冗余度小于給定閾值I*r時，該個體即被剔除。此外，隨著種群的逐代進化，具有預測適應值的個體可信度應該逐漸下降。設具有預測適應值的個體i在第t代的可信度為R(i，t)，則第t+1代的可信度R(i，t+1)可由式(32)更新得到。

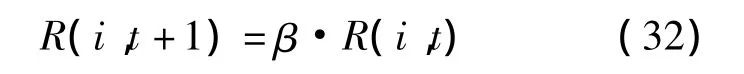
式中，β稱作可信度流失速率因子，且0＜β＜1

當個體的可信度R(i，t)下降到低于閾值R0時，該適應值不再可信，須從歷史種群數據庫中剔除。

4)適應值預測算法流程

S1:初始化歷史種群數據庫，初始種群置空，適應值置0，可信度置0;

S2:對于個體i，劃定其適應值共享區域Ωi，在歷史種群數據庫中找出Ωi包含的個體的集合S;

S3:按照式(28)計算個體i的適應值預測可信度R(i)，判斷若R(i)≥R*，則按照式(28)預測個體i的適應值;否則，計算個體i的真實適應值，并置其適應值可信度R(i)為1;

S4:將個體i添加到歷史種群數據庫中;

S5:判斷當前種群中是否每個個體都已經計算了適應值，是則轉S6，否則轉S2;

S6:對歷史種群數據庫進行如下更新:1)計算所有個體的冗余度Ir，剔除所有冗余個體;2)對于所有具有預測適應值的個體，按照式(32)更新其可信度R，剔除所有不可信個體。

3．4．2 算法的有效性驗證

數值實驗的目的為:測試算法的有效性，即測試該算法能多大程度地減少真實適應值的評價次數。采用文獻［20］中的 3個基準函數:(f1)Goldstein-Price，(f2)Six-Hump Camel-Back，(f3)Shekel’s Foxholes，對其進行測試。每個問題獨立運行20次，測試結果如表1所示。

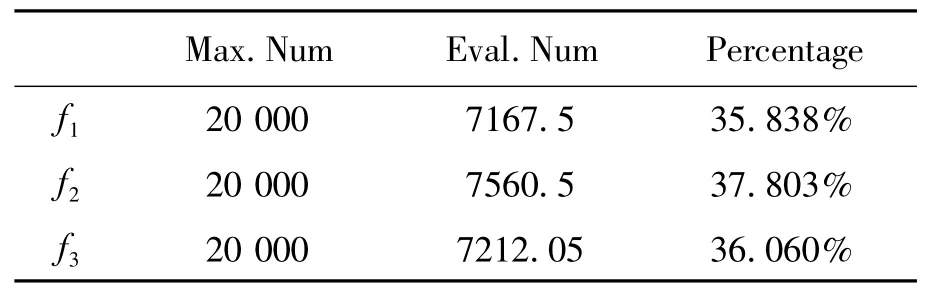
表1 算法有效性測試結果Tab．1 Validity test of algorithm

其中:“Max．Num”和“Eval．Num”分別表示真實適應值的最大可能計算次數和實際計算的平均次數，“Percentage”表示真實適應值計算的平均比例。

由表1可知，本文提出的預測模型大大減少真實適應值的計算次數，三個測試函數分別減少了64．162%，62．197%和 63．940%的適應值平均計算次數。這意味著，在適應值函數計算非常耗時的情況下，應用FAGA節省了大約2/3的計算時間。

圖4為高重合度人字齒輪動態特性優化流程圖。

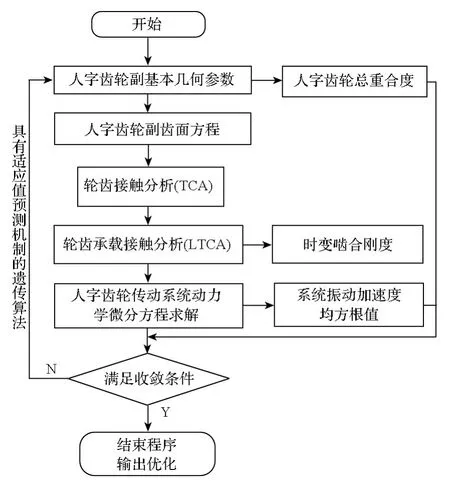
圖4 高重合度人字齒輪動態特性優化設計流程圖Fig．4 Flow chart of optimization for dynamic performance of double helical gearswith high contact ratio

4 優化實例及結果分析

考慮某航空用單級人字齒輪傳動，大、小齒輪材料相同，滲碳淬火，5級精度。齒輪基本參數如表2所示。

遺傳算法參數設置如下:種群大小為100，最大進化代數為50代，交叉概率為0．8，變異概率為0．3，共享半徑壓縮因子為0．2，可信度閾值為0．6，冗余度閾值為1E-7。

遺傳算法全局優化后得到適應度值曲線圖如圖5所示。

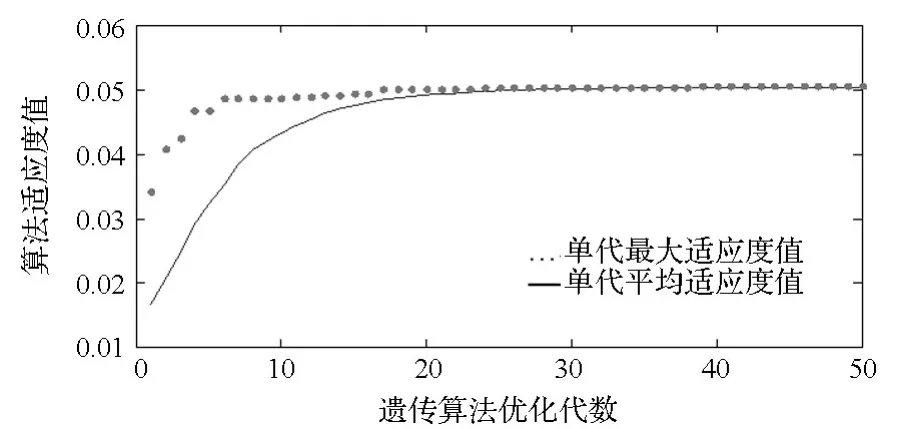
圖5 遺傳算法全局優化適應度值Fig．5 Fitness value of genetic algorithm optimization

圖5 中，單代平均適應度值是指優化進行每一代所有個體適應度值的平均值，它反映了這一代所有個體與全局最優解的趨近程度，單代最大適應度值則代表了本代個體適應度值的最大值，它反映了一代內的局部最優解所對應的適應度值。

觀察適應度值曲線可以看出，兩曲線在總體變化趨勢上基本保持了一致性，優化開始單代平均適應度值與單代最大適應度值迅速增加，優化至25代后，平均適應度值與最大適應度值均不再提高，迭代過程快速收斂，表明了本文提出的改進遺傳算法——FAGA的有效性。

將優化所得方案與原始設計進行對比，具體參數如表2所示。

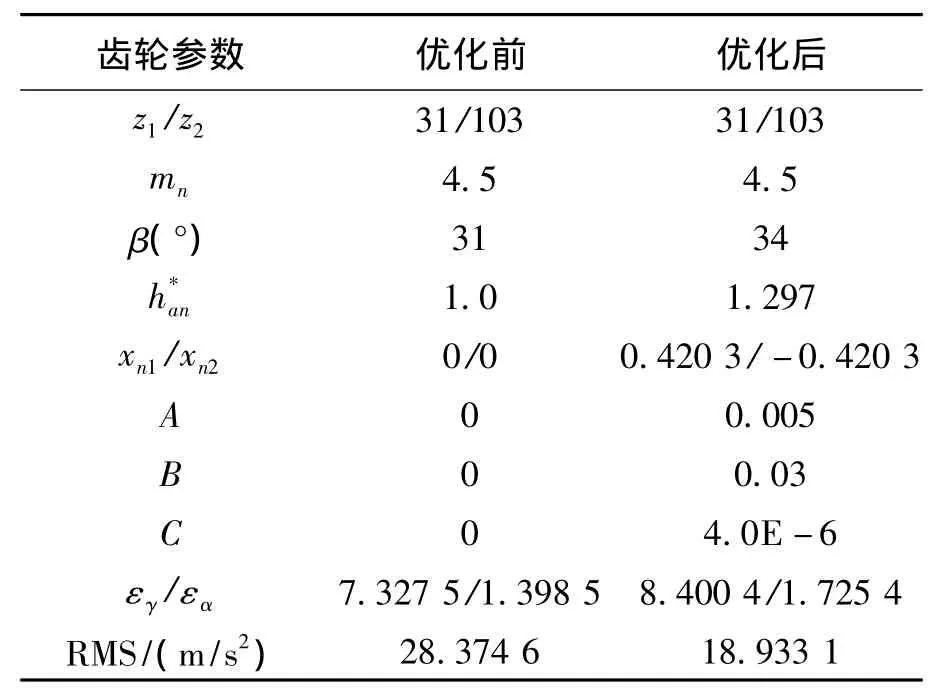
表2 優化前后齒輪參數Tab．2 Comparison of gear parameters before and after optimization

優化前后人字齒輪副沿嚙合線方向及軸向的振動加速度響應曲線分別如圖6和圖7所示。

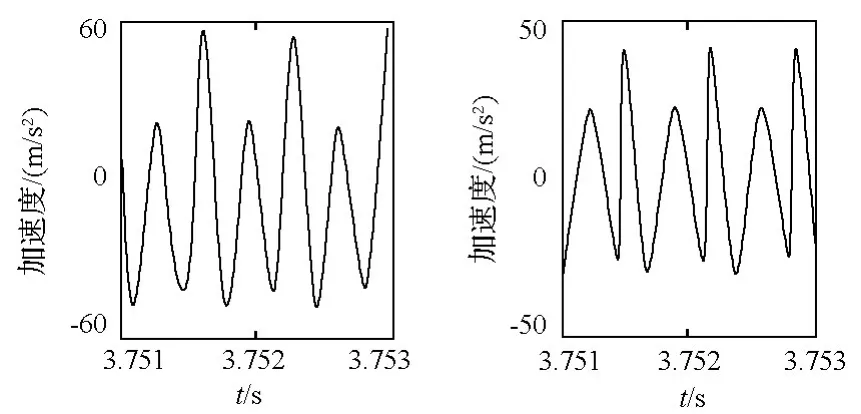
圖6 優化前后人字齒輪振動加速度響應(圓周方向)Fig．6 Comparison of vibration acceleration response before and after optimization(circumferential direction)

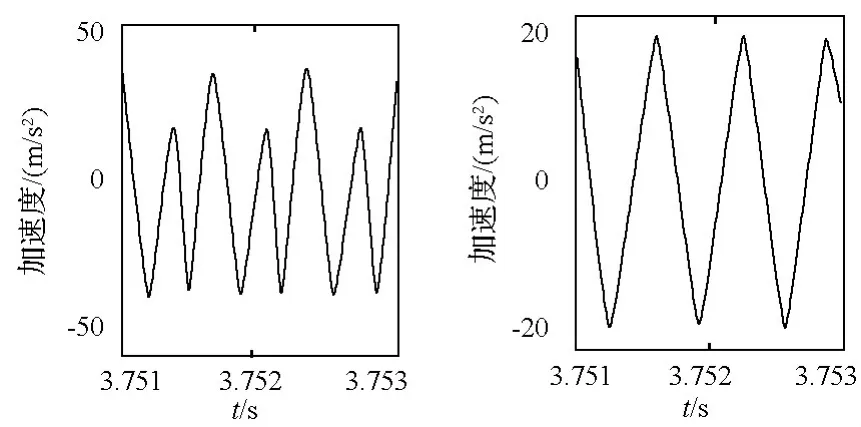
圖7 優化前后人字齒輪振動加速度響應(軸向)Fig．7 Comparison of vibration acceleration response before and after optimization(axial direction)

由表2可以看出，通過本次優化設計，人字齒輪的總重合度較優化前提高了約14．6%，端面重合度較優化前提高了23．4%，齒輪傳動較之前更加平穩。觀察優化前后人字齒輪的振動加速度響應曲線圖可以看出，經動態特性優化后，齒輪傳動的沿嚙合線方向及軸向的振動加速度值明顯降低，說明同時采用齒廓修形和齒向修形降低了齒輪傳動的扭轉振動和軸向振動。優化設計的目標函數即人字齒輪副沿嚙合線方向的振動加速度均方根值下降了約33%。

5 人字齒輪傳動動態試驗

由于齒輪傳動系統的振動噪聲與振動加速度的均方根值成正比。因此，本文對優化后的兩組齒輪進行了噪音水平檢測。

將加工的齒輪在高速齒輪減振降噪試驗臺上進行帶載試驗，試驗臺采用功率開放型齒輪試驗裝置，由原動機、受試驗的齒輪裝置和耗能負載裝置三部分組成，結構簡單，操作簡便。試驗臺的主要技術參數如下:直流調速電機的額定功率為200kW;直流調速電機的轉速范圍為300～1200r/min;試驗臺的最大封閉功率為2200kW;傳動齒輪箱速比為 1∶3．322。

噪聲測試分析系統主要包括傳聲器、放大器、噪聲采集系統、聲級計和磁帶記錄儀等。分析系統組成如圖8所示。

圖8 噪聲測試分析系統組成框圖Fig．8 Block diagram of noise test and analysis system

在試驗齒輪箱的右側及箱體后方距離測量表面1m處，共布置6個傳聲器，分別測量了動態性能優化前后在2000N·m及1000N·m扭矩作用下，電機轉速分別為 500r/min，750r/min，1000r/min時，6個測點上人字齒輪試驗箱的空氣噪音分貝值，將每個測點上獲得的三組噪聲測量值取平均值，計算得到兩種扭矩作用下噪音均值分別如表3、表4所示。

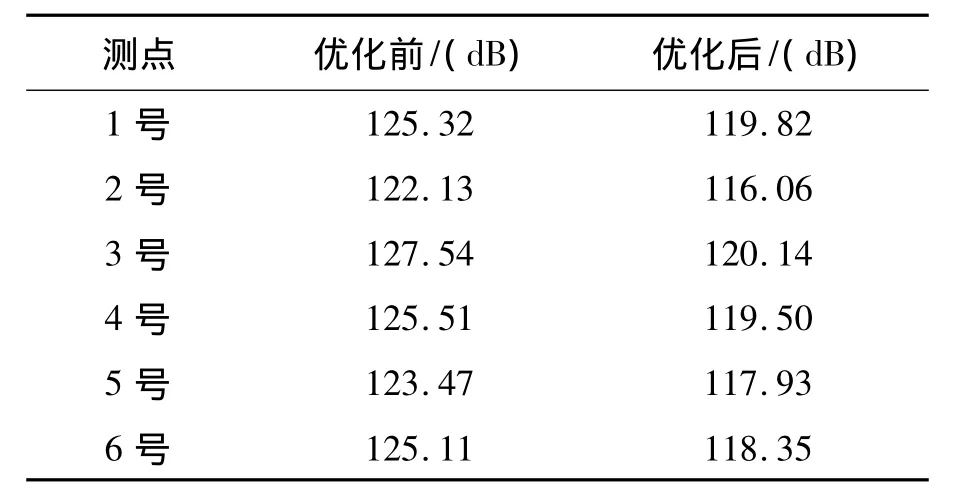
表3 優化前后齒輪副噪音水平(2000N·m)Tab．3 Comparison of gear noise value before and after optimization(2000N·m)

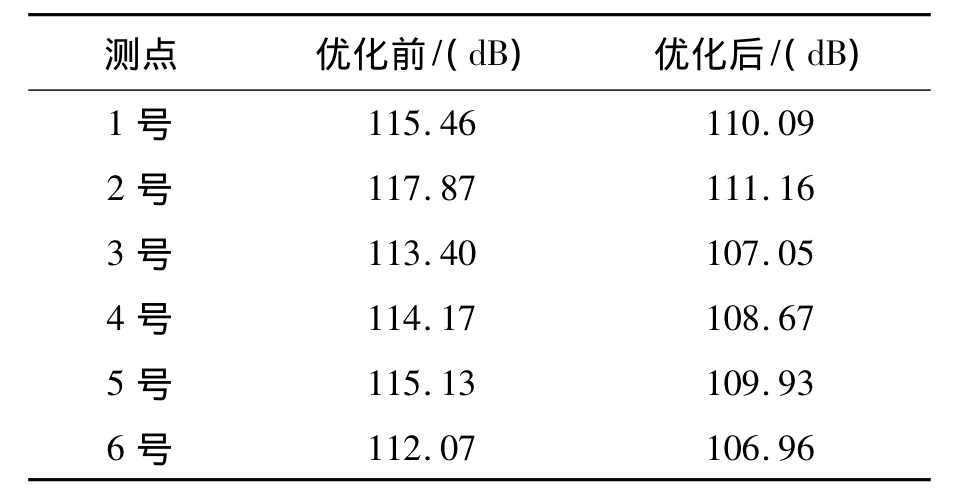
表4 優化前后齒輪副噪音水平(1000N·m)Tab．4 Comparison of gear noise value before and after optimization(1000N·m)

對比人字齒輪副動態性能優化前后的噪音分貝值，可以看出兩種扭矩作用下，優化后齒輪傳動的平均噪音水平下降了約5～7dB，試驗結果進一步說明了對人字齒輪副進行動態性能優化設計取得了良好的減振降噪效果。

6 結論

1)綜合考慮了齒輪傳動時變嚙合剛度、誤差激勵和嚙合沖擊激勵等因素，基于人字齒輪副承載接觸分析技術，針對人字齒輪主動齒輪軸向浮動的特點，應用集中質量法建立了考慮修形的人字齒輪副彎-扭-軸耦合非線性動力學模型，求解得到了人字齒輪傳動系統的振動加速度響應。

2)針對傳統遺傳算法在計算復雜工程問題時適應值計算費時的缺點，提出了一種具有適應值預測機制的遺傳算法——FAGA，以適應值的共享預測取代真實適應值的計算，提高了優化效率。

3)在對齒輪進行高重合度設計分析的基礎上，以人字齒輪左側齒輪沿嚙合線方向的振動加速度均方根值作為最優設計的目標函數，采用FAGA對齒輪傳動的動態性能進行了優化設計。實例表明，對人字齒輪進行動態特性優化后，齒輪傳動重合度增大的同時，齒輪嚙合線方向的振動加速度均方根值降低了約33%。

4)通過試驗，對比優化前后兩種扭矩作用下齒輪的噪音分貝值，可以看出優化后噪音分貝值下降了5～7dB，進一步說明了本文提出的優化設計方法對改善人字齒輪傳動的動態性能，減小齒輪傳動的振動及噪音具有一定的意義。

References)

［1］ Sivakumar P， Gopinath K， Sundaresh S． Performance evaluation of high-contact-ratio gearing for combat tracked vehicles-a case study［J］．Proceedings of the Institution of Mechanical Engineers，2010，224:631-643．

［2］ 杜雪松，朱才朝，寧杰．船用齒輪傳動的動態優化設計［J］．重慶大學學報，2011，34(5):14-18．DU Xuesong，ZHU Caizhao，NING Jie．Dynamic optimization design of marine gear transmission system［J］．Journal of Chongqing University，2011，34(5):14-18．(in Chinese)

［3］ 張慶偉．風力發電機齒輪傳動系統的動態優化設計［J］．重慶大學學報，2010，33(3):30-35．ZHANG Qingwei．Dynamic optimization design of gear transmission system for wind［J］．Journal of Chongqing University，2010，33(3):30-35．(in Chinese)

［4］ Pan Wusan．Optimal design of compact high contact ratio gears［D］．The University of Memphis，2006．

［5］ Reagor CP．An optimal gear designmethod forminimization of transmission error and vibration excitation［D］． The Pennsylvania State University，2010．

［6］ 齒輪手冊(上冊)［M］．機械工業出版社，2001，(2):5-7．Gear manual(volume one)［M］．Bei Jing:China Machine Press，2001，(2):5-7．(in Chinese)

［7］ Litvin F L，Kin V．Computerized simulation ofmeshing and bearing contact for single-enveloping worm-gear drives［J］．ASME Journal of Mechanical Design，1992，114(2):313-316．

［8］ Livtin F L．Gear geometry and applied theory［M］．PTR Prentice Hall，Englewood，1994．

［9］ 方宗德．修形斜齒輪的輪齒接觸分析［J］．航空動力學報，1997，12(3):247-250．FANGG Zongde．Tooth contact analysis ofmodification helical Gear［J］．Journal of Aerospace Power，1997，12(3):247-250．(in Chinese)

［10］ 李潤方，陶澤光，林騰蛟，等．齒輪嚙合內部動態激勵數值模擬［J］．機械傳動，2011，25(2):1-4．LIRunfang，TAO Zeguang，LIN Tengjiao，et al．Numerical simulation for inner dynamic excitation of gearing［J］．Journal of Mechanical Transmission，2011，25(2):1-4．(in Chinese)

［11］ 蘇進展，方宗德，蔡香偉，等．斜齒球形齒輪齒面接觸分析［J］．哈爾濱工業大學學報，2011，43(5):111-114．SU Jinzhan，FANG Zongde，CAI Xiangwei，et al．Contact characteristics of spherical helical gears［J］．Journal of Harbin Institute of Technology．2011，43(5):111-114．(in Chinese)

［12］ 方宗德．齒輪輪齒承載接觸分析(LTCA)的模型和方法［J］．機械傳動，1998，12(2):251-254．FANG Zongde．Load contact analysis of gears［J］．Journal of Mechanical Transmission，1998，12(2):251-254．(in Chinese)

［13］ 王成，方宗德，張墨林，等．人字齒輪傳動的動態特性分析［J］．哈爾濱工業大學學報，2011，43(7):122-126．WANG Cheng， FANG Zongde， ZHANG Molin， et al．Analysis of dynamics behavior for double helical gears［J］．Journal of Harbin Institute of Technology，2011，43(7):122-126．(in Chinese)

［14］ 唐增寶，鐘毅芳，陳久榮．修形參數對齒輪動態性能影響的分析研究［J］．機械傳動，1994，18(3):29-30．TANG Zengbao，ZHONG Yifang，CHEN Jiurong．Analysis for influences of profile modification parameters on dynamic characteris［J］．Journal of Mechanical Transmission，1994，18(3):29-30．(in Chinese)

［15］ 趙寧，郭輝，方宗德，等．直齒面齒輪修形及承載接觸分析［J］．航空動力學報，2008，23(11):2142-2146．ZHAO Ning，GUO Hui，FANG Zongde，et al．Modification and loaded contact analysis of spur face gears［J］．Journal of Aerospace Power，2008，23(11):2142-2146．(in Chinese)

［16］ 沈云波，方宗德，趙寧，等．齒廓方向修形的斜齒面齒輪嚙合特性研究［J］．中國機械工程，2008，19(18):2219-2222．SHEN Yunbo，FANG Zongde，ZHAO Ning，et al．Meshing performance ofmodified face gear drive with helical pinion in the profile direction［J］．China Mechanical Engineering，2008，19(18):2219-2222．(in Chinese)

［17］ 王成，方宗德，郭琳琳，等．人字齒輪齒廓修形優化設計與試驗研究［J］．西北工業大學學報，2010，28(2):224-227．WANG Cheng， FANG Zongde， GUO Linlin， et al．Modification optimization and test of double helical gears［J］．Journal of Northwestern Polytechnical University，2010，28(2):224-227．(in Chinese)

［18］ Goldberg D E，Richardson J．Genetic algorithm with sharingof multimodal function optimization［C］//Genetic Algorithms and Their Applications:Proceedings of the Second International Conference on Genetic Algorithms，Lawrence Erlbaum，1987:41-49．

［19］ 趙寧，趙永志，付晨曦．具有適應值預測機制的遺傳算法［J］．國防科技大學學報，2014，36(3):116-121．ZHAO Ning，ZHAO Yongzhi，FU Chenxi．Genetic algorithm with fitness approximate mechanism［J］．Journal of National University of Defense Technology，2014，36(3):116-121．(in Chinese)

［20］ 孫超利．面向機械系統優化設計的微粒群算法［M］．北京:機械工業出版社，2012．SUN Chaoli．Partical swarm optimization for optimal design of mechanical system［M］．Beijing:China Machine Press，2012．(in Chinese)