注入三次諧波擾動的分布式光伏并網逆變器孤島檢測技術

貝太周 王 萍 蔡蒙蒙

(天津大學電氣與自動化工程學院 智能電網教育部重點實驗室 天津 300072)

?

注入三次諧波擾動的分布式光伏并網逆變器孤島檢測技術

貝太周 王 萍 蔡蒙蒙

(天津大學電氣與自動化工程學院 智能電網教育部重點實驗室 天津 300072)

針對現有主動式孤島檢測方法中注入的高次諧波會導致檢測變慢及偶次諧波不易消除等問題，提出了與同步鎖相技術相結合的新型孤島檢測方法。首先在αβ坐標系下構建了頻率自適應鎖相器，用于快速準確地捕獲電網相位；然后研究了一種通過相位擾動實現三次諧波分量注入的具體方法，并確定了擾動系數的選擇依據，同時借助具有高速運算性能的滑動Goertzel濾波器對公共耦合點處的三次諧波電壓進行提取，以便能快速檢測系統是否發生孤島。最后通過仿真及實驗驗證了所提方法的可行性和有效性。

分布式光伏系統 孤島檢測 同步提取 頻率自適應控制 滑動Goertzel濾波器

0 引言

考慮到新型可再生能源清潔無污染及儲量豐富等諸多強力優勢，能源產業的結構調整正在世界范圍內廣泛興起。發展新型可再生替代能源，提高清潔電力供應，從長遠考慮，無論在技術提高、環境保護，還是在經濟發展等方面都將會有實質性的促進意義[1]。

以太陽能、風能、生物質能等主導型可再生能源建立發展起來的分布式發電系統(Distributed Generation System，DGS)旨在為用戶提供優質、清潔、高效能的電力資源。分布式發電系統以其經濟、高效等諸多優勢，已在可再生電力能源產業中獲得了新發展。分布式發電系統中的孤島現象通常理解為：當主電網因電氣故障、檢修或誤操作等原因與分布式發電系統失聯后，發電系統作為獨立電源將繼續對本地負載供電[2]，形成獨立不可控的自給電力系統。按照孤島檢測標準UL 17417和IEEE Std1547的相關規定，任何分布式并網發電系統必須具有孤島檢測功能[3]，并在規定時間內迅速完成檢測，及時封鎖逆變器。

主動式檢測方法通常采用對逆變器控制中的某個參量(如電流頻率[4]、電流相位[5]、電流幅值[6]、電流諧波[7]和電壓[8]等)施加擾動的措施，來觀測公共耦合點(Point of common coupling，PCC)處的某些參量變化，以判斷是否發生孤島[9]。主動式檢測方法的首要問題是擾動信號的選定。如果擾動信號頻率過高，則會放大本地負載品質因數的作用，導致孤島難檢；如果采用偶次諧波作為擾動，偶次諧波又難以消除。縱觀與孤島檢測相關的大部分文獻資料，很少有學者結合電壓同步技術提出相應的孤島檢測新方法。此類方法的關鍵在于如何平衡擾動與同步鎖相的關系[10，11]，換言之，施加的擾動不能改變或影響同步提取信號中的電壓過零點的位置。孤島檢測的另一個重要問題在于檢測的快速性，而快速性的實現則需要依托具有較少運算量的數據處理算法來完成。

本文首先在由頻率自適應同步鎖相器所得的相位角上整周期地注入一個小幅的正弦擾動，然后通過具有高速運算性能的滑動Goertzel濾波器提取vPCC中由擾動相位帶來的三次諧波電壓，并與孤島檢測閾值比較，來判定系統是否發生孤島。最后由仿真及實驗驗證所提方法的可行性及有效性。

1 檢測方法的具體實現

圖1所示為用于評估本文所提出的孤島檢測算法的單相分布式光伏并網逆變系統。逆變器采用了受PWM調制能實現并網電流可控的H橋拓撲，輸出電流經LC濾波器濾除其中的高頻分量。

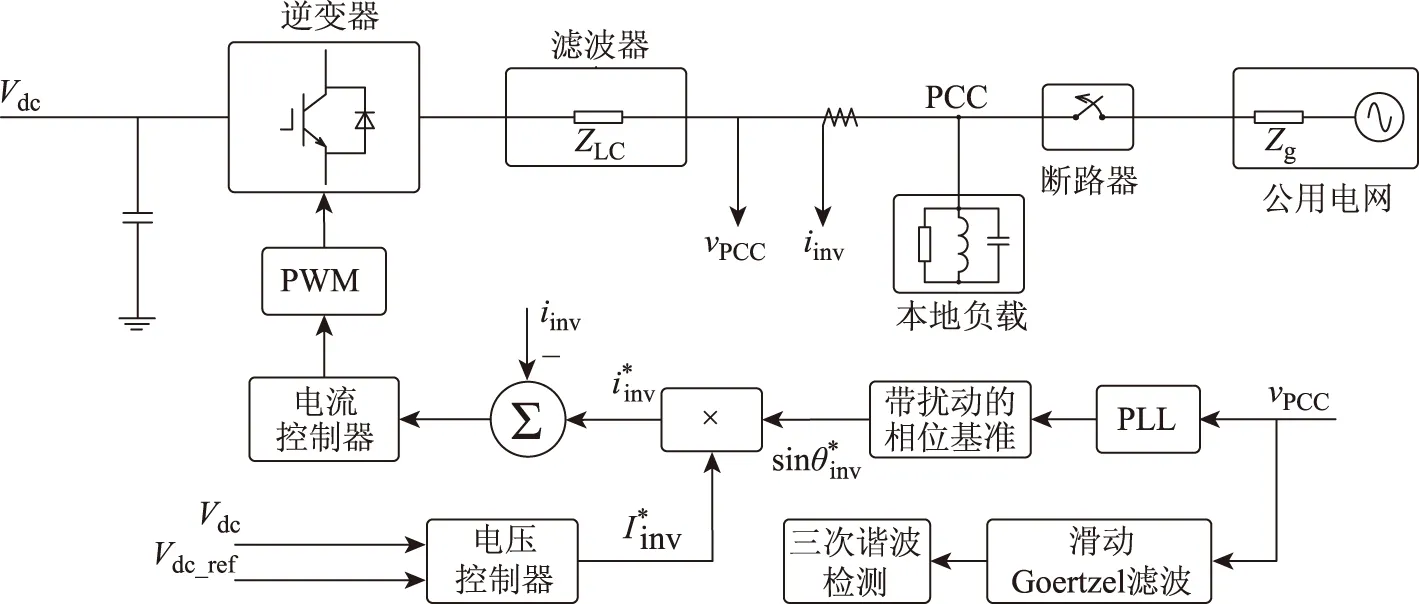
圖1 單相分布式光伏并網逆變系統Fig.1 Single phase distributed grid-connected inverter

DGS分別工作于并網模式和孤島模式時，PCC處主導阻抗的不同導致此處的三次諧波電壓也不同。僅考慮電路中的三次諧波分量，圖1所示結構的簡化電路如圖2所示。圖2中Iinv_150 Hz為逆變器輸出電流中的三次諧波，Vg_150 Hz為電網中的三次諧波。

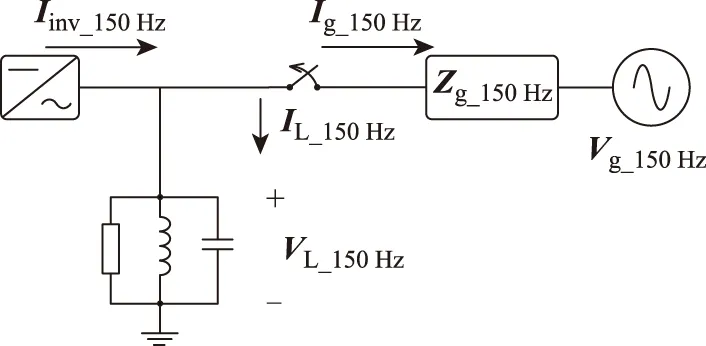
圖2 DGS中逆變器的簡化電路Fig.2 Simplification of the inverter in DGS

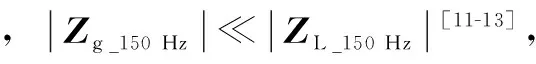
VPCC_150 Hz=(ZL_150 Hz‖Zg_150 Hz)Iinv_150 Hz
≈Zg_150 HzIinv_150 Hz

(1)

當DGS工作于孤島模式時，公共耦合點處的復阻抗即為本地負載的復阻抗，因此，PCC處的三次諧波電壓矢量表達式為

VPCC_150 Hz=ZL_150 HzIinv_150 Hz

(2)

本地負載的阻抗可根據式(3)求得。

(3)

式中，fr、Q分別為RLC的諧振頻率和品質因數。

用于孤島檢測的標準負載品質因數Q為2.5[2]，取本地RLC負載的諧振頻率fr為50 Hz[9]，因此RLC各參數可按上述參數指標根據式(3)來選取臨界值且在實際情況下允許存在微小偏差[9]。

1.1 鎖相實現

為了快速而準確地獲取電網的相位信息，本方案采用圖3所示的鎖相結構。在正交信號發生器[14]中借助移相算子a=e-j90°實現從PCC處的電壓vPCC到αβ坐標系下電壓分量vα和vβ的虛擬構建。

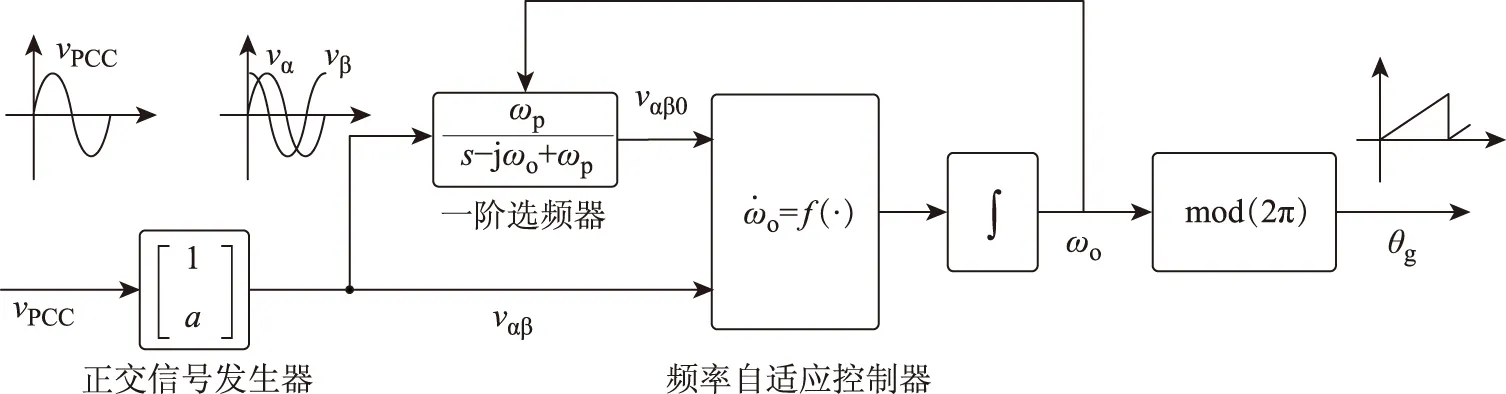
圖3 頻率自適應鎖相結構Fig.3 Structure of the frequency-adaptive-based PLL

為了選取電網中特定的基波分量，圖3中特別引入了式(4)所描述的一階選頻器[14]

(4)

式中，ωo和ωp分別為選頻器的中心頻率和截止頻率。

選頻器的性能主要取決于ωp的選值。圖4所示為在中心頻率ωo=50 Hz時，不同ωp值情況下選頻器對單位階躍輸入x(t)=-ε(t-0.02)的動態響應特性曲線。觀察圖4可發現：較低的ωp會導致系統響應過慢，并伴有振蕩產生；而較高的ωp能夠保證響應的快速性，且響應過程中不存在振蕩現象。另外，從圖5所示的一階選頻器Bode圖上可看出，當ωp取值過大時，會導致選頻器的選頻特性變差，不利于基頻信號的提取。所以綜合考慮響應的動態性能和對基頻信號的有效提取，取截止頻率ωp為0.707倍的電網基波頻率ω，即ωp=0.707ω[14]。

選頻器的幅頻函數為

(5)

結合圖5可看出，當選頻器的中心頻率ωo等于實際電網基波頻率ω時，可對基波信號進行無衰減零相移地提取，而對其他頻率信號將會有不同程度地衰減和相位偏移。

圖4 一階選頻器的單位階躍響應Fig.4 Unit step response of the first-order frequency selector

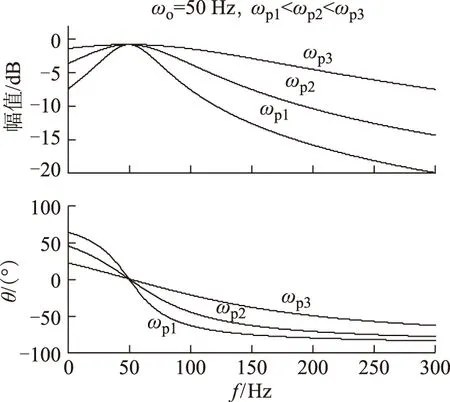
圖5 不同ωp值時選頻器的Bode圖Fig.5 Bode plot of the frequency selector with different values of ωp

? 考慮到實際工況下電網基波頻率為非定值，若采取自適應調整算法，則可保證一階選頻器的中心頻率ωo能按當前的電網基波頻率實時地自我更新，從而無衰減零相移地提取出基波分量。對不斷更新的中心頻率作進一步處理，便可得到電網的相位信息。這正是圖3所示的頻率自適應同步鎖相結構設計和實現的基本要義。

電壓分量vα和vβ在經過選頻器FS(s)前后可分別表示為

(6)

(7)

圖3中，頻率自適應控制器的調整律定義為

(8)

式中，δ為頻率自適應調整系數。

結合式(5)～式(7)，可將式(8)所描述的自適應調整律變換為

(9)

特別地，當中心頻率ωo等于或無限接近于電網基波頻率ω時，式(9)可近似為

(10)

頻率自適應動態調節過程為：當ω>ωo時，根據式(10)可及時調整ωo線性增大；當ω<ωo時，可及時調整ωo線性減小；當ωo經過自適應調整等于ω時，ωo保持不變。因此，自適應調整律的實質在于：當電網基波頻率ω改變時，迫使鎖相輸出ωo朝著消除這種改變的方向移動。而頻率自適應調整的過程同時又是鎖相環對電網相位自調整輸出的過程。合理選取頻率自適應調整系數δ，有助于提高頻率調整的快速性[15]。

1.2 擾動相位的產生及影響

如前所述，施加的擾動不能改變或影響同步提取信號中電壓過零點位置的原則，方案中將一個由三角函數確定的擾動量σinj整周期地正向(亦可負向)注入到當前同步鎖相角θg中，作為DGS并網控制中的相位基準角。此派生方法的具體實現如圖6所示。

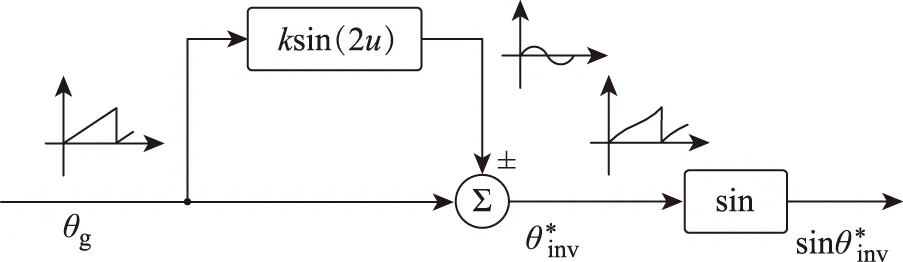
圖6 擾動相位的生成Fig.6 Generation of the disturbed phase

定義注入的擾動相位為

σinj=ksin2θg

(11)

式中，k為用于孤島檢測時的相位擾動系數。

此時，含有擾動的相位基準為

(12)

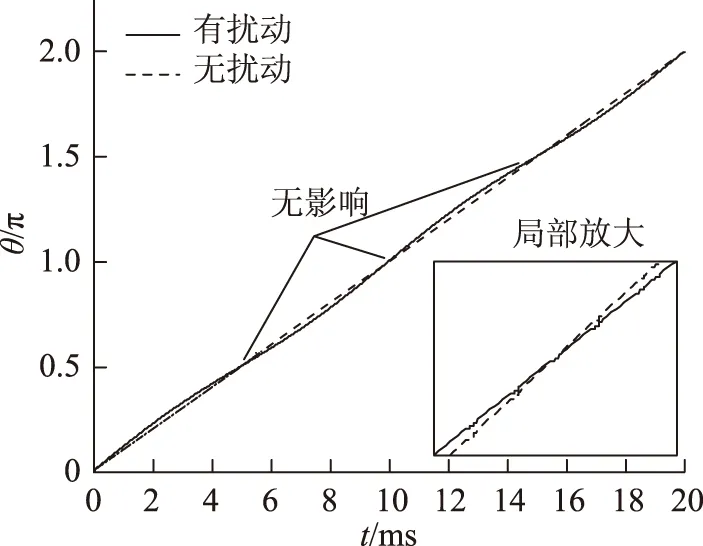
圖7 擾動相位對鎖相的影響Fig.7 Influence of the disturbed phase on PLL

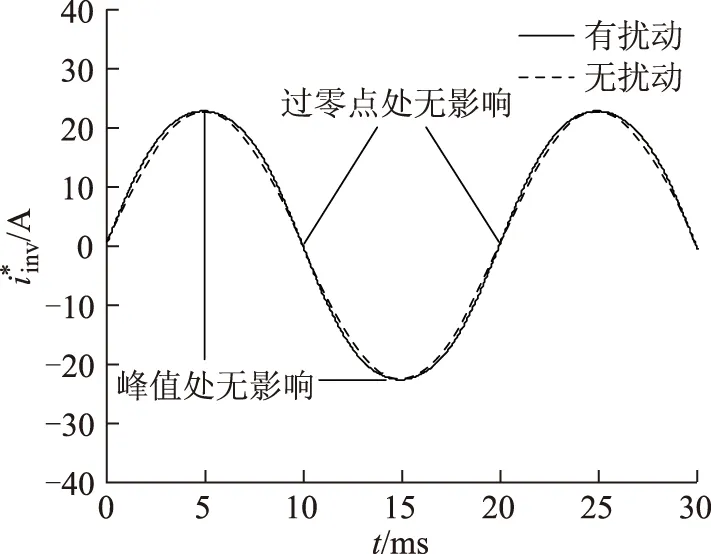
圖8 擾動相位對的影響

結合式(12)，單位化的并網基準電流表示為

(13)

參照式(14)及其導出式(15)

(14)

(15)

以及在擾動系數k足夠小時，描述的等價關系為

cos(ksin2θg)≈1
sin(ksin2θg)≈ksin2θg

(16)

對式(13)進行逐步推算，最終得到

(17)

因此，在擾動系數k取值足夠小的情況下，式(11)所描述的相位擾動量σinj在逆變器并網控制的基準電流中產生了如式(18)所描述的三次諧波電流分量

(18)

事實上，擾動系數k更重要的作用在于它直接表征了引入的相位擾動量所帶來的并網電流總諧波畸變率(THD)和三次諧波含量的百分比。表1按照仿真結果給出了不同k值情況下對應的THD分布及三次諧波含量的百分比。

表1 不同k值時并網電流的THD及三次諧波含量Tab.1 The THD and 3rd ATHD of the grid-connected current with different values of k

根據國家對并網逆變器電能質量相關標準中規定的并網電流THD值不能超過5%以及注入電網的三次諧波電流必須低于4%的技術要求，按照表1給出的數據，如果采用本文所提的相位擾動注入法進行孤島檢測，需要考慮到并網逆變器引起的電能質量問題和接入電網背景諧波，那么擾動系數k的取值上限應低于0.08，且應根據實際工程條件具體給出。

1.3 vPCC中諧波分量的提取

在對實數信號進行連續采樣并計算DFT頻譜時，SDFT濾波器雖然運算量較少，但濾波器系數的截斷誤差易導致自身的非穩定性[12，16]。如果對式(19)所描述的SDFT的z域傳遞函數的分子分母同時乘以分母的共軛因子1-e-j2πm/Nz-1，將會得到式(20)。

(19)

(20)

式中，N為工頻周期內總的采樣點數；m為與擾動頻率相對應的特定頻點。若擾動頻率、采樣頻率和電網基波頻率分別表示為fdist、fsam和fg，則N和m在取值上將受式(21)的約束。

(21)

觀察式(20)發現，變換后的HSDFT(z)可理解為在傳統的Goertzel濾波器前級聯了一個N階梳狀濾波器。由此構成的滑動Goertzel濾波器框圖如圖9所示。其中的數值關系如式(22)、式(23)所示。

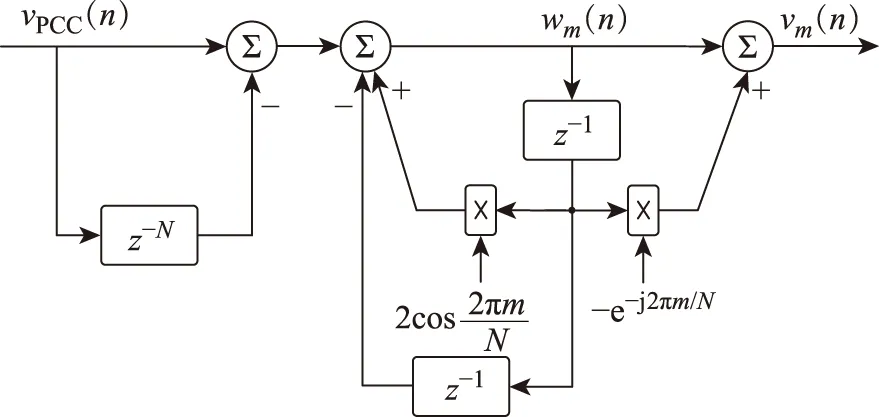
圖9 滑動Goertzel濾波器框圖Fig.9 Diagram of the sliding Goertzel filter

(22)

vm(n)=wm(n)-wm(n-1)e-j2πm/N

(23)

結合式(22)及式(23)，可得到

vm(n)=vPCC(n)-vPCC(n-N)-wm(n-2)+
wm(n-1)ej2πm/N

(24)

從式(24)可看出，根據n-1和n-2時刻的頻譜值，經過3個實加和1個復加運算后，便可得到n時刻的頻譜值，而滑動DFT則需要6個實乘和3個復加運算[16]才能得到同樣結果。因此，采用滑動Goertzel濾波器計算n時刻的頻譜值，將會大大降低運算量。n時刻采樣值的m次頻譜值可由式(25)求得。

(25)

通過式(25)求得三次諧波電壓值，將其與由式(1)確定的孤島檢測閾值作比較，即可判斷DGS是否發生孤島。為避免檢測時由于暫態分量及噪聲等因素導致的孤島誤檢，實際應用中還應在孤島檢測算法內根據IEEE 929-2000的規定設置必要的延時時間。

2 仿真及實驗驗證

參數設置如下：直流側電壓為400 V，電網參數為220 V/50 Hz，電網內抗1.8 mH，LC濾波器參數為5 mH/47 nF，開關管的開關頻率為20 kHz，采樣頻率為1 kHz，本地RLC并聯負載的諧振頻率設置為50 Hz，負載的品質因數Q為2.5(相應參數設置為R=174.8 Ω，L=220 mH，C=45 μF)。相位擾動系數k為0.06，頻率自適應調整系數δ為0.918。

圖10為頻率自適應控制器的動態響應曲線以及單相光伏系統在并網運行時的電流輸出。

圖10 頻率自適應動態調整及并網電流波形Fig.10 Dynamic adjustment of the frequency-adaptive law and the grid-connected current wave

設定電網頻率分別在0.025 s和0.055 s時瞬間完成頻率突變。如圖10a所示，當電網頻率發生突變時，頻率自適應控制器可保證系統在極短時間內(約為半個工頻周期)準確跟蹤并將自身中心頻率更新到當前頻率，從而提高了鎖相的快速性與準確性。圖10b描述了逆變器并網運行時的電流輸出。從波形上看，為了孤島檢測的需要，即使在并網控制基準相位中注入了擾動，也能保證逆變器在并網運行時始終以單位功率因數可靠運行。

為了更好地評估孤島檢測的性能，在弱電網(純電感電網阻抗，Lg=1.8 mH)條件下進行了仿真測試。測試時間為0.3 s、0.1 s時逆變器工作狀態由并網運行瞬時切換為孤島運行。以下測試結果按照本地負載為純電阻負載(R=17.48 Ω)和RLC并聯負載(R=174.8 Ω，L=220 mH，C=45 μF)兩種情況依次給出，測試結果分別如圖11和圖12所示，兩種負載情況下均考慮了電網中三次諧波電壓的情形。

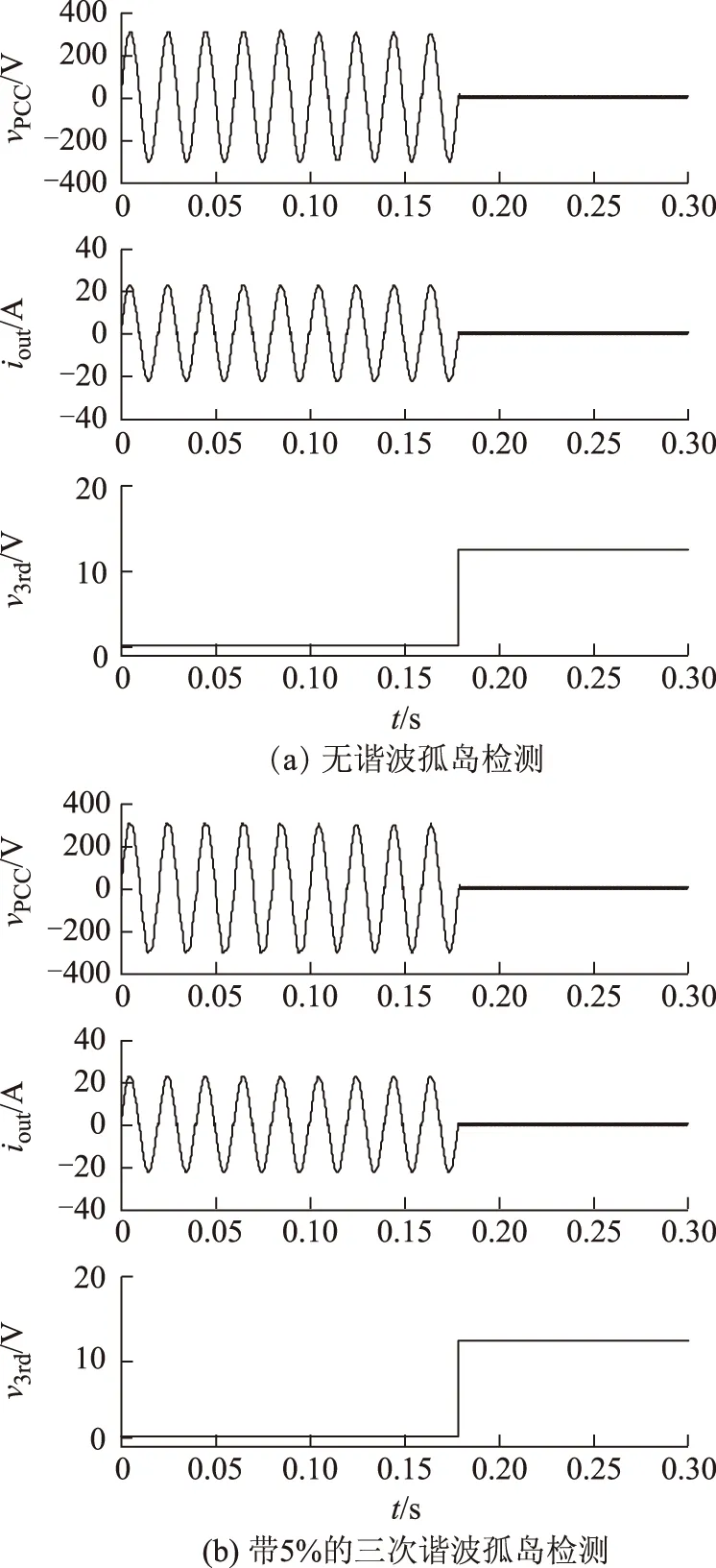
圖11 本地負載為純電阻負載時的仿真結果Fig.11 Simulation results with R load

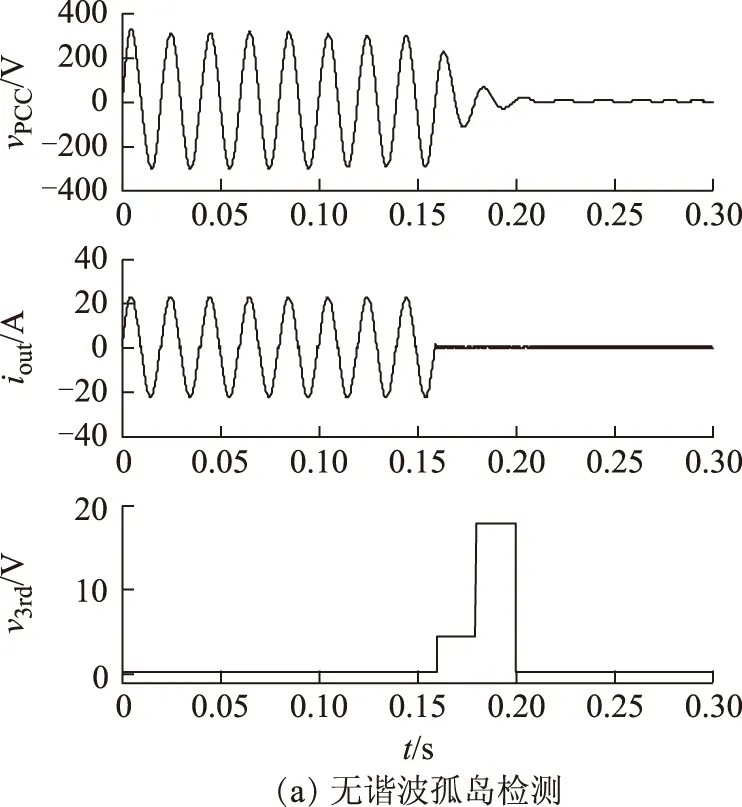
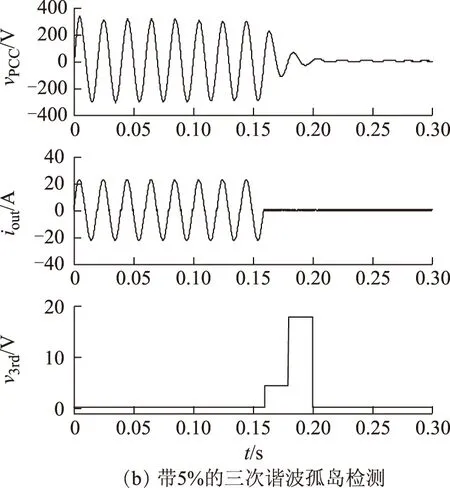
圖12 本地負載為RLC并聯負載時的仿真結果Fig.12 Simulation results with RLC load

圖11a及圖11b的前兩圖顯示了逆變器脫離電網后，PCC上的電壓和電流的動態響應情況，后一圖給出了檢測到的PCC處三次諧波的變化過程。結果顯示，電網中自身存在的三次諧波電壓對孤島檢測的動態性能影響不大，所提方案均能在80 ms內迅速完成孤島檢測。本地負載為RLC并聯負載時的檢測結果如圖12所示。結論與上面的分析類似，電網中的三次諧波同樣對孤島檢測的動態性能以及時效性影響不大。當本地負載為RLC并聯負載時，逆變器從離網到封鎖所用的時間約為60 ms。

以上兩種負載情形下的檢測封鎖時間均符合IEEE 929-2000標準。另外，在同等條件下本文方案的孤島檢測時間明顯短于文獻[11]中的孤島檢測時間(103～104 ms)，這主要歸因于采用的滑動Goertzel濾波器在運算上的快速性。

在實驗室條件下分別就頻率自適應控制器的動態響應及孤島檢測進行了實驗驗證。為了更好地反映出頻率自適應調整的動態性能以及輸入信號頻率的可調性，實驗中采用10 V/25 Hz的方波信號來模擬頻率變化。得到的頻率自適應調整的動態響應曲線如圖13所示(U1代表實際頻率，U2代表響應頻率)。實驗結果顯示，當實際信號的頻率發生變化后，按照本文提出的頻率自適應調整律，響應頻率可在極短的時間內，快速收斂于實際頻率。

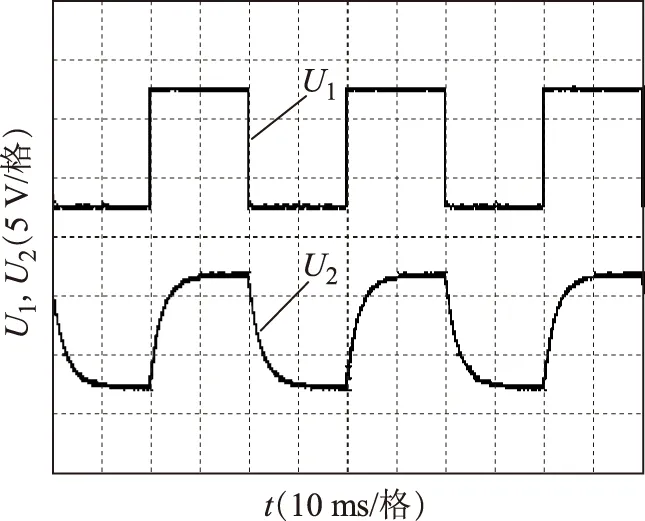
圖13 頻率自適應動態調整實驗波形Fig.13 Dynamic adjustment of the frequency-adaptive law

在4.8 kW單相并網逆變器上進行了孤島檢測算法的實驗驗證。實驗參數為：直流側母線電壓400 V；電網參數為220 V/50 Hz；濾波器參數和開關頻率與仿真時相同；本地負載采用10 Ω的純電阻負載；控制芯片采用TI公司研發的TMS320F28335DSP。圖14所示為逆變器并網運行時電網電壓及并網電流的實驗波形圖。從圖中可看出，即使在并網電流控制中注入一定量的相位擾動，也不會導致逆變器的輸出電流與電網電壓存在相位差。孤島檢測的實驗結果如圖15所示。當逆變器切離電網后，借助滑動Goertzel濾波器進行孤島判定，可在80 ms內完成檢測并封鎖逆變器，使輸出電流為零。

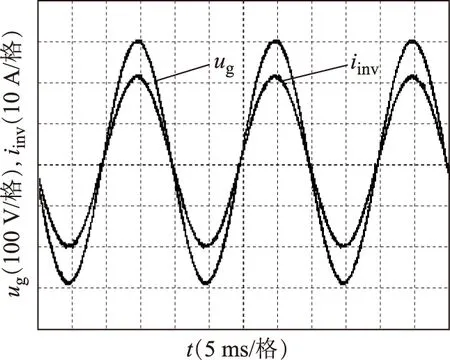
圖14 并網運行時的電網電壓及并網電流實驗波形Fig.14 Waves of the grid voltage and grid-tied current in the grid-connected situation

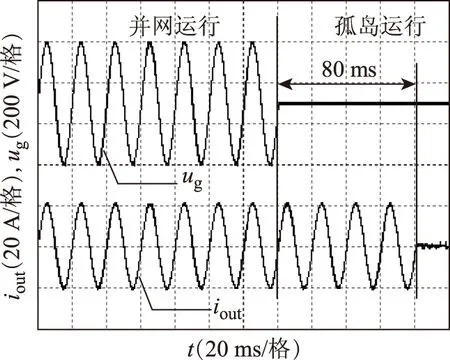
圖15 孤島檢測時電網電壓及輸出電流實驗波形Fig.15 Waves of the grid voltage and outputting current in the islanding situation

3 結論

首先通過頻率自適應鎖相器獲得了電網的相位角，然后提出了實現向并網電流注入少量三次諧波的相位擾動法，并通過滑動Goertzel濾波器對PCC處三次諧波電壓的快速提取實現孤島檢測。最后通過仿真和實驗驗證了方案的可行性和有效性。

[1] Sozer Y，Torrey D A.Modeling and control of utility interactive inverters[J].IEEE Transactions on Power Electronics，2009，24(11)：2475-2483.

[2] IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems[S].IEEE Standard 1547-2003：16.

[3] 蔡逢煌，鄭必偉，王武.結合同步鎖相的光伏并網發電系統孤島檢測技術[J].電工技術學報，2012，27(10)：202-206. Cai Fenghuang，Zheng Biwei，Wang Wu.Islanding detection method combined with PLL for photovoltaic grid-connected power system[J].Transactions of China Electrotechnical Society，2012，27(10)：202-206.

[4] 楊滔，王鹿軍，張沖，等.基于無功電流-頻率正反饋的孤島檢測方法[J].電力系統自動化，2012，36(14)：193-199. Yang Tao，Wang Lujun，Zhang Chong，et al.A novel islanding detection method based on positive feedback between reactive current and frequency[J].Automation of Electric Power Systems，2012，36(14)：193-199.

[5] 劉芙蓉，康勇，王輝，等.主動式移相式孤島檢測的一種改進的算法[J].電工技術學報，2010，25(3)：172-176. Liu Furong，Kang Yong，Wang Hui，et al.An improved active phase shift method for islanding detection[J].Transactions of China Electrotechnical Society，2010，25(3)：172-176.

[6] 楊秋霞，趙清林，郭小強.三相光伏并網逆變器電流擾動孤島檢測建模及分析[J].電力系統自動化，2012，36(4)：45-49. Yang Qiuxia，Zhao Qinglin，Guo Xiaoqiang.Modeling and analysis of current-disturbance based islanding detection for three-phase photovoltaic grid-connected inverters[J].Automation of Electric Power Systems，2012，36(4)：45-49.

[7] Timbus A V，Teodorescu R，Blaabjerg F.Online grid measurement and ENS detection for PV inverter running on highly inductive grid[J].IEEE Transactions on Power Electronics，2004，2(3)：77-82.

[8] 郭小強，鄔偉揚.微電網非破壞性無盲區孤島檢測技術[J].中國電機工程學報，2009，29(25)：7-12.Guo Xiaoqiang，Wu Weiyang.Non-devastating islanding detection for microgrids without non-detection zone[J].Proceedings of the CSEE，2009，29(25)：7-12.

[9] 闞加榮，羅運虎，謝少軍，等.基于下垂特性鎖相環的反孤島性能分析[J].電工技術學報，2013，28(4)：165-170. Kan Jiarong，Luo Yunhu，Xie Shaojun，et al.Analysis with anti-islanding performance of grid-connected inverters based on drooped PLL[J].Transactions of China Electrotechnical Society，2013，28(4)：165-170.

[10]Ciobotaru M，Vassilios G，Teodorescu A R，et al.Accurate and less-disturbing active antiislanding method based on PLL for grid-connected converters[J].IEEE Transactions on Power Electronics，2010，25(6)：1576-1584.

[11]Velasco D，Trujillo C，Garcera G，et al.An active anti-islanding method based on phase-PLL perturbation[J].IEEE Transactions on Power Electronics，2011，25(4)：1056-1066.

[12]鐘誠，井天軍，楊明皓.基于周期性無功電流擾動的孤島檢測新方法[J].電工技術學報，2014，29(3)：270-276. Zhong Cheng，Jing Tianjun，Yang Minghao.A new islanding detection method with periodic reactive current disturbance[J].Transactions of China Electrotechnical Society，2014，29(3)：270-276.

[13]Kim J H，Kim J G，Ji Y H，et al.An islanding detection method for a grid-connected system based on the goertzel algorithm[J].IEEE Transactions on Power Electronics，2011，26(4)：1049-1055.

[14]Golestan S，Monfared M，Freijedo F D，et al.Performance improvement of a prefiltered synchronous-reference-frame PLL by using a PID-type loop filter[J].IEEE Transactions on Industrial Electronics，2014，61(7)：3469-3479.

[15]杜雄，王國寧，孫鵬菊，等.采用正弦幅值積分器的電網基波電壓同步信號檢測[J].中國電機工程學報，2013，33(36)：104-111. Du Xiong，Wang Guoning，Sun Pengju，et al.Synchronization signal detection for grid fundamental voltage through employing sinusoidal amplitude integrators[J].Proceedings of the CSEE，2013，33(36)：104-111.

[16]Jacobsen E，Lyons R.The sliding DFT[J].IEEE Signal Processing Magazine，2003，20(2)：74-80.

An Islanding Detection Method with the Third Harmonic Injection for Distributed Grid-Connected PV Inverters

BeiTaizhouWangPingCaiMengmeng

(Key Laboratory of Smart Grid of Ministry of Education School of Electrical Engineering and Automation Tianjin University Tianjin 300072 China)

A new islanding detection method combining with synchronization phase lock technology is presented in view of the deficiencies of current active islanding detection approaches，such as a slow-response due to the injected high frequency harmonics and the even harmonics persistence.Firstly a frequency-adaptive PLL is constructed in αβ coordinates to capture the phase of the grid fast and accurately.Then the third harmonic injection by phase perturbation is provided and the criterion for selecting the appropriate disturbance coefficients has also been given.The sliding Goertzel filter with the high-speed computational property is applied to extract the third-harmonic component of the PCC voltage，with the intention of determining whether the system is in an islanding situation.Finally both feasibility and availability of the proposed method are verified through simulations and experiments.

Distributed PV system，islanding detection，synchronous extraction，frequency adaptive control，sliding Goertzel filter

高等學校博士學科點專項科研基金(20120032110070)資助項目。

2014-12-24 改稿日期2015-01-12

TM46

貝太周 男，1984年生，博士研究生，研究方向為分布式光伏并網系統運行與控制。(通信作者)

王 萍 女，1959年生，教授，博士生導師，研究方向為分布式新能源發電及電能質量控制。