凹型端齒削弱永磁直線電機(jī)端部力波動(dòng)方法

彭 兵 劉鐵法 張 囡 夏加寬 荊汝寶 孫宜標(biāo)

(沈陽工業(yè)大學(xué)電氣工程學(xué)院 沈陽 110870)

?

凹型端齒削弱永磁直線電機(jī)端部力波動(dòng)方法

彭 兵 劉鐵法 張 囡 夏加寬 荊汝寶 孫宜標(biāo)

(沈陽工業(yè)大學(xué)電氣工程學(xué)院 沈陽 110870)

結(jié)合端面磁通函數(shù)和虛位移法推導(dǎo)PMLM端部效應(yīng)產(chǎn)生的單端推力波動(dòng)和法向力波動(dòng)的解析表達(dá)式，揭示端部效應(yīng)引起的推力波動(dòng)和法向力波動(dòng)的規(guī)律。通過對(duì)傅里葉級(jí)數(shù)的分析，提出反相位補(bǔ)償原理的凹型端齒結(jié)構(gòu)，該結(jié)構(gòu)能消除推力波動(dòng)和法向力波動(dòng)的奇次諧波，解決傳統(tǒng)的優(yōu)化動(dòng)子長度削弱推力波動(dòng)但帶來電機(jī)縱向“俯仰運(yùn)動(dòng)趨勢(shì)”的缺點(diǎn)，同時(shí)還能消除動(dòng)子橫向“俯仰運(yùn)動(dòng)趨勢(shì)”。最后以齒槽效應(yīng)較弱的12槽11極PMLM為例，采用有限元仿真和實(shí)驗(yàn)驗(yàn)證，結(jié)果證明該方法能夠削弱端部效應(yīng)產(chǎn)生的法向力波動(dòng)和推力波動(dòng)。

永磁直線電機(jī) 端部效應(yīng) 端部效應(yīng)法向力波動(dòng) 端部效應(yīng)推力波動(dòng) 凹型端齒

0 引言

氣浮或磁浮的永磁直線電機(jī)直接驅(qū)動(dòng)系統(tǒng)是高精密加工與高精密定位領(lǐng)域的主要發(fā)展方向之一，它要求直線電機(jī)具有優(yōu)異的推力和法向力性能[1-4]。然而，永磁直線電機(jī)特有的縱向端部效應(yīng)導(dǎo)致動(dòng)子受到一定的法向力波動(dòng)和推力波動(dòng)(統(tǒng)稱為端部力)，影響了加工或定位精度。

國內(nèi)外文獻(xiàn)將齒槽效應(yīng)和縱向端部效應(yīng)產(chǎn)生的推力波動(dòng)合稱為detent force，而縱向端部效應(yīng)detent force是推力波動(dòng)的一個(gè)主要原因[5，6]。半無限長動(dòng)子是分析端部detent force的經(jīng)典模型，文獻(xiàn)[5-8]均是基于該模型優(yōu)化動(dòng)子長度或端齒結(jié)構(gòu)實(shí)現(xiàn)端部detent force的最小化，其中端部detent force的解析式是基于有限元仿真分析得出，缺乏嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)模型和波動(dòng)值的量化。等效磁網(wǎng)絡(luò)模型是分析端部detent force的另外一個(gè)重要方法，文獻(xiàn)[9，10]均是基于此模型的基礎(chǔ)上，采用能量法預(yù)測(cè)端部detent force，得到減小端部detent force的合適的端齒形狀，其端部detent force的解析表達(dá)式較復(fù)雜，難以預(yù)測(cè)端部detent force的特征。有導(dǎo)軌永磁直線電機(jī)動(dòng)、定子之間強(qiáng)大的法向電磁吸引力一方面對(duì)負(fù)載平臺(tái)的強(qiáng)度有較高要求，另一方面引起摩擦力的攝動(dòng)，法向電磁吸力的平均力是單邊平板型永磁直線電機(jī)研究的熱點(diǎn)[11-14]。文獻(xiàn)[15]指出齒槽效應(yīng)和端部效應(yīng)是引起法向力波動(dòng)的主要原因，研究了齒槽法向力波動(dòng)機(jī)理和磁極三段錯(cuò)位削弱齒槽法向力波動(dòng)的方法，從控制的角度提出了分相補(bǔ)償抑制端部效應(yīng)引起的法向力波動(dòng)，但未從電機(jī)本體設(shè)計(jì)上給出削弱端部法向力波動(dòng)的方法。上述文獻(xiàn)均未分析削弱推力波動(dòng)的方法對(duì)法向力波動(dòng)的影響規(guī)律。

端部效應(yīng)是影響電機(jī)法向力波動(dòng)和推力波動(dòng)的一個(gè)重要原因，本文以短初級(jí)永磁直線電機(jī)為研究對(duì)象，首先利用端部邊緣磁通函數(shù)和虛位移法推導(dǎo)出端部效應(yīng)引起的法向力波動(dòng)和推力波動(dòng)的解析表達(dá)式，分析其主要諧波與電機(jī)長度參數(shù)的關(guān)系；然后從相位補(bǔ)償角度分析錯(cuò)落結(jié)構(gòu)端齒削弱端部力波動(dòng)的原理，提出了“凹”型端齒結(jié)構(gòu)；最后以12槽11極永磁直線電機(jī)為例，分別采用有限元仿真和實(shí)驗(yàn)驗(yàn)證該方法的有效性。

1 基于磁通函數(shù)的端部力解析分析

1.1 端部磁通函數(shù)

假設(shè)鐵心磁導(dǎo)率為無窮大；永磁體的磁導(dǎo)率與空氣相同；永磁體向外磁路提供的磁通為Φm。在無槽永磁直線電機(jī)中，永磁磁極發(fā)出的磁通可近似認(rèn)為是一簇簇的同心圓(根據(jù)磁路最短原理，該封閉曲線實(shí)際為橢圓，見圖1d)。當(dāng)電機(jī)動(dòng)子運(yùn)行時(shí)，穿過初級(jí)電樞鐵心縱向端面的磁通發(fā)生周期性變化。在x=0，如圖1a位置時(shí)，次級(jí)的交軸q1與初級(jí)的左邊緣重合，永磁體S1提供的一半磁通都穿過縱向端面邊緣，此時(shí)，穿過初級(jí)電樞鐵心左端面的磁通最大，最大值為Φ=Φm/2；隨著動(dòng)子的運(yùn)行，穿過端面的磁通越來越少，在x=τ/2，如圖1c位置時(shí)，穿過初級(jí)電樞鐵心左端面的磁通為零，即Φ=0；當(dāng)初級(jí)繼續(xù)向右運(yùn)動(dòng)時(shí)，穿過初級(jí)電樞鐵心左端面的磁通逐漸變大，當(dāng)運(yùn)行到x=τ，如圖1d所示位置時(shí)，穿過初級(jí)電樞鐵心左端面的磁通又變?yōu)樽畲螅?Φm/2。當(dāng)動(dòng)子繼續(xù)向右運(yùn)行時(shí)，又重復(fù)著上述的周期變化，可見初級(jí)電樞鐵心左端面的磁通函數(shù)波長為極距τ。

圖1 端部磁通示意圖Fig.1 Schematic diagram of magnetic flux through the edge

由上述定性分析，結(jié)合有限元仿真，可得到穿過動(dòng)子縱向端面的磁通曲線，如圖2所示。

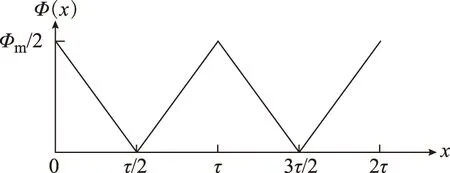
圖2 縱向端部邊緣磁通Φ(x)與x的近似關(guān)系Fig.2 Approximate relationship between Φ(x) and x

由圖2可寫出穿過縱向端面的磁通Φ(x)方程式

(1)

另外一端端面的磁通具有相似的變化規(guī)律，二者僅存在相位差，相位差取決于動(dòng)子長度。設(shè)動(dòng)子總長度為Ls，將(Ls+x)代入式(1)中，就可得到右端面的磁通方程。

1.2 端部力解析分析

由圖1可看出，臨近動(dòng)子鐵心左側(cè)的磁極(圖1a～圖1c的S1，圖1d的N2)產(chǎn)生的磁通穿過動(dòng)子鐵心縱向左側(cè)端面，最終回到動(dòng)子鐵心下的磁極(圖1a～圖1c的N2，圖1d的S2)中。隨著動(dòng)子位置的變化，穿過端面的磁通也發(fā)生了變化，等效認(rèn)為磁極N2(或S2) 與動(dòng)子鐵心間的磁場(chǎng)儲(chǔ)能發(fā)生了變化。根據(jù)電磁場(chǎng)知識(shí)可知，等效后的氣隙磁場(chǎng)儲(chǔ)能為

(2)

式中，B為磁感應(yīng)強(qiáng)度；μ0為真空磁導(dǎo)率；Φ為穿過電樞鐵心縱向端部的磁通；S等效為半個(gè)磁極包圍的面積；δ為考慮開槽后的等效氣隙長度。

1)端部效應(yīng)法向力

根據(jù)虛位移原理可知，左端端部效應(yīng)引起的法向力及波動(dòng)為

(3)

式(3)傅里葉級(jí)數(shù)為

(4)

由式(4)可看出，端部效應(yīng)引起的單端法向力不僅包含恒定的電磁吸引力，還包含所有次法向力諧波，各次諧波的波長為τ/n。

用(Ls+x)代替式(4)中的x，則得到電機(jī)動(dòng)子右端部法向力。如果Ls=kτ，電機(jī)動(dòng)子左、右端部法向力完全一致；如果Ls=kτ+τ/2，電機(jī)動(dòng)子左、右端部法向波動(dòng)力的奇次諧波反相位，偶次諧波同相位，將會(huì)造成動(dòng)子縱向“俯仰運(yùn)動(dòng)趨勢(shì)”。

2)端部效應(yīng)推力

同樣根據(jù)虛位移原理可得左端部效應(yīng)引起的推力波動(dòng)為

(5)

式(5)傅里葉級(jí)數(shù)為

(6)

由式(6)可看出，端部效應(yīng)引起的單端推力波動(dòng)包含所有次諧波，各次諧波的波長為τ/n。

用(Ls+x)代替式(6)中的x，則得到電機(jī)動(dòng)子右端部所受推力。如果Ls=kτ，電機(jī)動(dòng)子左、右端部所受推力完全一致，整個(gè)電機(jī)受到的推力波動(dòng)為二者的波動(dòng)之和；如果Ls=kτ+τ/2，電機(jī)動(dòng)子左、右端部所受推力的奇次諧波反相位，偶次諧波同相位，將會(huì)消除奇次推力波動(dòng)，只剩下偶次推力諧波，動(dòng)子受到的推力波動(dòng)幅值約為Ls=kτ電機(jī)的2倍。

2 凹型端齒削弱端部力波動(dòng)

根據(jù)式(4)和式(6)可知，端部效應(yīng)引起的單端推力波動(dòng)和法向力波動(dòng)的基波波長均為τ，二者相差90°電角度。法向力二次諧波的峰值僅為基波的1/4，推力二次諧波的峰值僅為基波的1/2，可見，如果能消除端部力的基波分量，將能極大的削弱法向力和推力的波動(dòng)。

對(duì)于式(4)中任意次法向力諧波的表達(dá)式為

(7)

如果將縱向邊端齒設(shè)計(jì)成如圖3所示單級(jí)樓梯步結(jié)構(gòu)，兩個(gè)端面的寬度相等，錯(cuò)落尺寸為Δx，則第一部分端部效應(yīng)產(chǎn)生的n次法向力FNLn1=FNLn，用x+Δx代替式(7)中的x得出第二部分端部效應(yīng)產(chǎn)生的n次法向力表達(dá)式

(8)則電機(jī)動(dòng)子單端受到的n次法向力的合力為FNLn1+FNLn2。由式(7)、式(8)可知，當(dāng)2πnΔx/τ=π，即Δx=τ/2n時(shí)，兩個(gè)錯(cuò)落端面受到的n次法向力的相位相差180°，得以相互抵消，其原理如圖3所示。同理，該方法也抵消了n次推力諧波。當(dāng)Δx=τ/2時(shí)，兩個(gè)錯(cuò)落面端部力的奇次諧波相位均相反，僅剩下偶次諧波，法向力波動(dòng)值約為傳統(tǒng)端齒結(jié)構(gòu)電機(jī)的1/4，單端推力波動(dòng)約為1/2，單級(jí)樓梯步型端齒電機(jī)動(dòng)子的推力波動(dòng)幅值與傳統(tǒng)端齒電機(jī)(動(dòng)子長度為Ls=kτ+τ/2)基本相同。

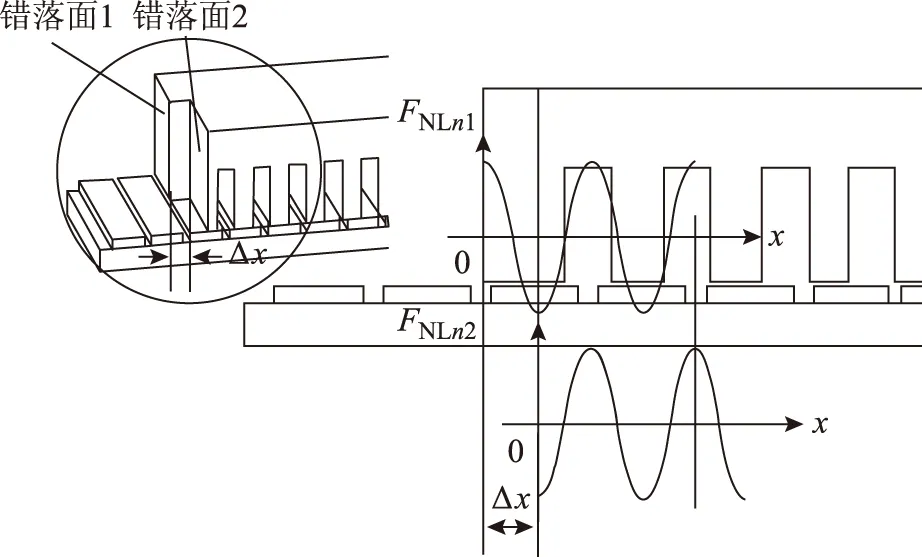
圖3 單級(jí)樓梯步端齒法的原理圖Fig.3 Schematic of single level staircase of end tooth method

這種單級(jí)樓梯步型端齒結(jié)構(gòu)使得電機(jī)動(dòng)子沿橫向受到的法向力和推力不均等，引起電機(jī)橫向“俯仰運(yùn)動(dòng)”趨勢(shì)和推力縱向“拉扯”趨勢(shì)。基于此，提出“凹”型端齒結(jié)構(gòu)，邊齒的中間凹入部分寬度是兩側(cè)凸出部分寬度的2倍，圖4為采用“凹”型端齒結(jié)構(gòu)的12槽11極PMLSM的三維模型及原理圖。

圖4 凹型端齒結(jié)構(gòu)法Fig.4 Concave profile method of end tooth

由于端齒沿橫向?qū)ΨQ，“凹”型端齒結(jié)構(gòu)法電機(jī)的動(dòng)子能夠在不發(fā)生橫向“俯仰運(yùn)動(dòng)趨勢(shì)”和推力縱向“拉扯趨勢(shì)”情況下，消除n次端部力(包括法向力和推力)。

3 仿真與實(shí)驗(yàn)

本文以齒槽法向力波動(dòng)較弱的12槽11極永磁直線電機(jī)為例驗(yàn)證“凹”型端齒結(jié)構(gòu)削弱端部力波動(dòng)的有效性，電機(jī)參數(shù)見表1。根據(jù)Δx=τ/2n可求出端部錯(cuò)落尺寸為Δx=8 mm，“凹”型端齒電機(jī)的動(dòng)子長度Ls=192 mm。作為對(duì)比實(shí)驗(yàn)的非“凹”型端齒電機(jī)動(dòng)子長度Ls=184 mm，Δx=0(工程應(yīng)用中，為減小推力波動(dòng)，傳統(tǒng)端齒電機(jī)動(dòng)子長度大多選為Ls=kτ+τ/2)。

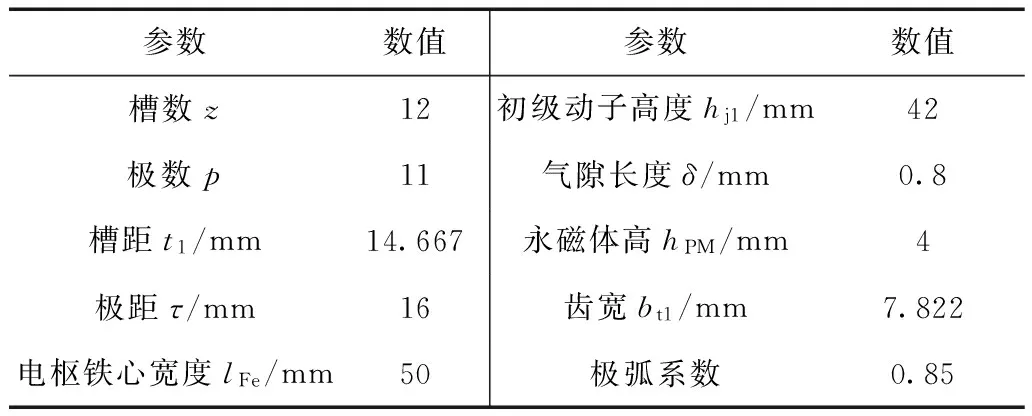
表1 電機(jī)參數(shù)Tab.1 Motor parameters

3.1 凹型端齒電機(jī)單端端部力波動(dòng)的仿真分析

在仿真端部力時(shí)，采用了半無限長電機(jī)模型。圖5a為一個(gè)動(dòng)子右半無限長電機(jī)，可仿真左端部受力；同理可建立一個(gè)動(dòng)子左半無限長電機(jī)仿真右端部受力。仿真時(shí)，動(dòng)子向右運(yùn)行，運(yùn)行的距離為τ。仿真結(jié)果如圖5b及圖5c所示，仿真結(jié)果均濾除了恒定分量，包括后文的實(shí)驗(yàn)結(jié)果也作了同樣處理。

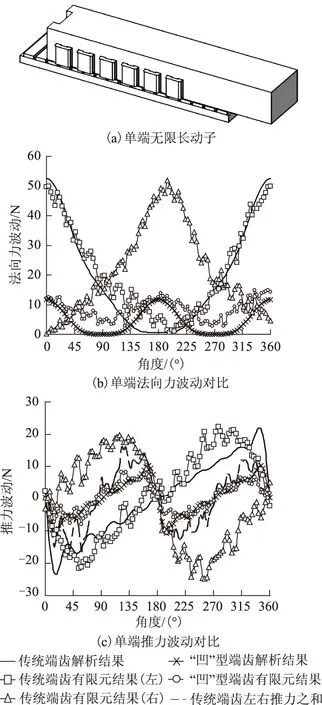
圖5 單端端部力仿真結(jié)果Fig.5 Simulation results of the single end force

由圖5可知，傳統(tǒng)端齒電機(jī)法向力和推力波動(dòng)主要次諧波分量的波長為τ，左端部的法向力和推力波動(dòng)與右端部力波動(dòng)相位相反，動(dòng)子有縱向“俯仰運(yùn)動(dòng)趨勢(shì)”，兩個(gè)端部的推力波動(dòng)之和的波形與“凹”型端齒電機(jī)單端推力波動(dòng)一致，幅值約為其2倍，這與1.2節(jié)的解析結(jié)果一致。采用“凹”型端齒結(jié)構(gòu)電機(jī)的單端法向力和推力波動(dòng)主要次諧波分量的波長變?yōu)棣?2，法向力波動(dòng)值約為傳統(tǒng)端齒電機(jī)的1/4，單端的推力波動(dòng)值約為傳統(tǒng)端齒電機(jī)的1/2，兩個(gè)端部受到的法向力和推力波動(dòng)大小與相位基本相同(本文仿真只給出了一個(gè)端部力的波動(dòng)波形)，這與解析結(jié)果相一致，有限元仿真結(jié)果證明“凹”型端齒結(jié)構(gòu)能有效消除單端端部力的主要次諧波，從而削弱了法向力和推力波動(dòng)及動(dòng)子有縱向“俯仰運(yùn)動(dòng)趨勢(shì)”。對(duì)于“凹”型端齒電機(jī)不會(huì)因?yàn)橐搿鞍肌毙投她X而改變電機(jī)的氣隙磁場(chǎng)和繞組因素，所以不會(huì)影響電機(jī)的平均推力。

3.2 “凹”型端齒結(jié)構(gòu)電機(jī)的實(shí)驗(yàn)

永磁直線電機(jī)法向力波動(dòng)和推力波動(dòng)靜態(tài)測(cè)試系統(tǒng)如圖6所示。

圖6 端部力靜態(tài)測(cè)試系統(tǒng)Fig.6 Static measurement system of the end force

該系統(tǒng)由檢測(cè)與顯示單元組成，檢測(cè)與顯示單元包括光柵尺、4個(gè)測(cè)量法向力的FC-WM微型拉力傳感器及BVM-300-4M四通道拉力測(cè)試儀、一個(gè)測(cè)量推力的拉力計(jì)及數(shù)顯拉力計(jì)表等。利用輔助安裝裝置將4個(gè)拉力傳感器安裝在工作臺(tái)和電機(jī)動(dòng)子之間，并調(diào)節(jié)預(yù)緊力；測(cè)量推力的拉力傳感器安裝在動(dòng)子與進(jìn)給裝置之間。當(dāng)調(diào)節(jié)進(jìn)給裝置帶動(dòng)動(dòng)子在導(dǎo)軌上移動(dòng)時(shí)，由光柵尺測(cè)量動(dòng)子的相對(duì)位移，由數(shù)顯表讀出位移值。由拉力測(cè)試儀采集4個(gè)法向力傳感器數(shù)據(jù)，由數(shù)顯拉力計(jì)表讀出推力波動(dòng)值。

圖7為采用“凹”型端齒結(jié)構(gòu)前、后的實(shí)驗(yàn)對(duì)比結(jié)果。由圖7a可知，“凹”型端齒結(jié)構(gòu)電機(jī)的單端法向力波動(dòng)的主要諧波波長為τ/2，而傳統(tǒng)端齒電機(jī)為τ；“凹”型端齒結(jié)構(gòu)電機(jī)單端的法向力波動(dòng)幅值約為傳統(tǒng)端齒電機(jī)的1/4，法向力波動(dòng)被有效削弱，實(shí)驗(yàn)結(jié)果與理論分析一致。由圖7b可知，動(dòng)子長度Ls=kτ+τ/2=184 mm、△x=0的傳統(tǒng)非“凹”型端齒電機(jī)與“凹”型端齒結(jié)構(gòu)電機(jī)的推力波動(dòng)基本一致；“凹”型端齒電機(jī)的整個(gè)動(dòng)子受到的推力波動(dòng)約為單端推力波動(dòng)的2倍，實(shí)驗(yàn)結(jié)果與解析分析的波形趨勢(shì)一致，進(jìn)一步證明了所提出解析法的可靠性。

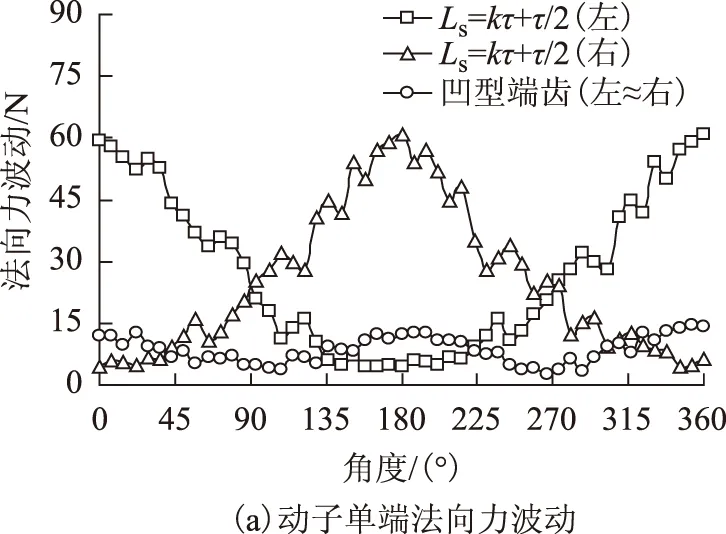
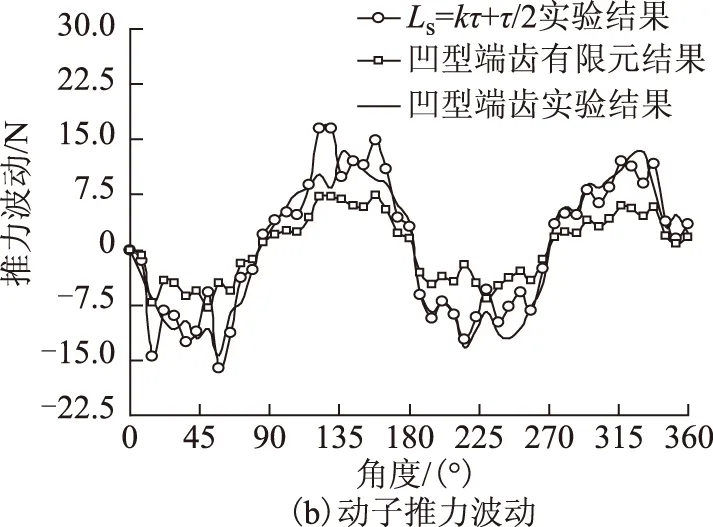
圖7 端部力靜態(tài)測(cè)試結(jié)果Fig.7 Static measurement results of the end force

4 結(jié)論

本文研究了永磁直線電機(jī)動(dòng)子縱向端部磁通變化規(guī)律與單端法向力波動(dòng)和推力波動(dòng)之間的內(nèi)在關(guān)系，提出“凹”型端齒結(jié)構(gòu)削弱端部力波動(dòng)的方法，通過解析分析、有限元仿真和實(shí)驗(yàn)驗(yàn)證，得出如下結(jié)論：

1)動(dòng)子“凹”型端齒結(jié)構(gòu)永磁直線電機(jī)相較于傳統(tǒng)端齒電機(jī)，單端法向力主要諧波的次數(shù)提高了1倍，幅值約為傳統(tǒng)端齒電機(jī)的1/4；單端推力主要諧波的次數(shù)也提高了1倍，幅值約為傳統(tǒng)端齒電機(jī)的1/2。

2)“凹”型端齒結(jié)構(gòu)永磁直線電機(jī)整個(gè)動(dòng)子受到的推力波動(dòng)為單端推力波動(dòng)的2倍，與動(dòng)子長度為Ls=kτ+τ/2電機(jī)的波動(dòng)次數(shù)與波動(dòng)幅值基本相同，但消除了Ls=kτ+τ/2電機(jī)的動(dòng)子縱向“俯仰運(yùn)動(dòng)趨勢(shì)”。

3)以一臺(tái)12槽11極永磁直線電機(jī)為例，將解析結(jié)果與仿真結(jié)果及實(shí)驗(yàn)值相比較，前者與后兩者的波形基本吻合，證明了解析計(jì)算與“凹”型端齒結(jié)構(gòu)削弱端部力波動(dòng)的可靠性和有效性。

[1] 李小平，李志科，陳學(xué)東，等.納米精度運(yùn)動(dòng)臺(tái)電機(jī)伺服參數(shù)校準(zhǔn)方法研究[J].中國電機(jī)工程學(xué)報(bào)，2009，29(21)：87-92. Li Xiaoping，Li Zhike，Chen Xuedong，et al.Calibration method for motor servo parameters of nano-precision motion stage[J].Proceedings of the CSEE，2009，29(21)：87-92.

[2] Young-Man Choi，Dae-Gab Gweon.A high-precision dual-servo stage using halbach linear active magnetic bearings[J].IEEE/ASME Transactions on Mechatronics，2011，16(5)：925-931.

[3] Owen R B，Maggiore M，Apkarian J.A high-precision，magnetically levitated positioning stage：toward contactless actuation for industrial manufacturing[J].IEEE Control Systems Magazine，2006，26(3)：82-95.

[4] Li Hong，Zhou Yunfei，Shi Yangchun.Motion control for wafer stage of 0.1 μm lithography[C].IEEE International Conference on Integration Technology，Shenzhen，China，2007：338-342.

[5] Zhu Z Q，Xia Z P，Howe D，et al.Reduction of cogging force in slotless linear permanent magnet motors[J].IEE Proceedings Electric Power Applications，1997，144(4)：277-282.

[6] Zhu Yu-wu，Lee Sang-Gun，Chung Koon-Seok，et al.Investigation of auxiliary poles design criteria on reduction of end effect of detent force for PMLSM[J].IEEE Transactions on Magnetics，2009，45(6)：2863-2866.

[7] 徐月同，傅建中，陳子辰.永磁直線同步電機(jī)推力波動(dòng)優(yōu)化及實(shí)驗(yàn)研究[J].中國電機(jī)工程學(xué)報(bào)，2005，25(12)：122-126. Xu Yuetong，F(xiàn)u Jianzhong，Chen Zichen.Thrust ripple optimization and experiment for PMLSM[J].Proceedings of the CSEE，2005，25(12)：122-126.

[8] 潘開林，傅建中，陳子辰.永磁直線同步電機(jī)的磁阻力分析及其最小化研究[J].中國電機(jī)工程學(xué)報(bào)，2004，24(4)：112-115. Pan Kailin，F(xiàn)u Jianzhong，Chen Zichen.Detent force analysis and reduction of PMLSM[J].Proceedings of the CSEE，2004，24(4)：112-115.

[9] 王昊，張之敬，劉成穎.永磁直線同步電機(jī)定位力分析與實(shí)驗(yàn)研究[J].中國電機(jī)工程學(xué)報(bào)，2010，30(15)：58-63. Wang Hao，Zhang Zhijing，Liu Chengying.Detent force analysis and experiment for permanent magnet linear synchronous motor[J].Proceedings of the CSEE，2010，30(15)：58-63.

[10]Xu Xiaozhuo，Wang Xudong，Si Jikai，et al.Detent force analysis and optimization for vertical permanent-magnet linear synchronous motor with fractional-slot windings[J].Journal of Computers，2013，8(3)：756-763.

[11]盧琴芬，張新敏，黃立人，等.錯(cuò)位式雙邊型永磁直線同步電機(jī)優(yōu)化設(shè)計(jì)[J].電工技術(shù)學(xué)報(bào)，2013，28(11)：35-41. Lu Qinfen，Zhang Xinmin，Huang Liren，et al.Optimal design of shifted type double-sided permanent magnet linear synchronous motors[J].Transactions of China Electrotechnical Society，2013，28(11)：35-41.

[12]陸華才，江明，郭興眾，等.永磁直線同步電機(jī)推力波動(dòng)約束[J].電工技術(shù)學(xué)報(bào)，2012，27(3)：128-132. Lu Huacai，Jiang Ming，Guo Xingzhong，et al.Thrust ripple suppression for permanent magnet linear synchronous motor[J].Transactions of China Electrotechnical Society，2012，27(3)：128-132.

[13]Profumo F，Tenconi A，Gianolio G.Design and realization of a PM linear synchronous motor with a very high thrust/normal force ratio[C].Industry Applications Conference，Chicago，USA，2001：1984-1988.

[14]Overboom T T，Smeets J P C，Jansen J W，et al.Semianalytical calculation of the torque in a linear permanent-magnet motor with finite yoke length[J].IEEE Transactions on Magnetics，2012，48(11)：3575-3578.

[15]沈麗.高精度永磁直線伺服電機(jī)法向力波動(dòng)分析與抑制方法研究[D].沈陽：沈陽工業(yè)大學(xué)，2014.

A Method for Reducing the End Effect Force Fluctuation by the Concave Profile End-tooth in Permanent Magnet Linear Motors

PengBingLiuTiefaZhangNanXiaJiakuanJingRubaoSunYibiao

(Electric Engineering Institute of Shenyang University of Technology Shenyang 110870 China)

Analytical expressions of the normal component and the thrust component of the end force are obtained by integrating the virtual displacement principle，which is described by the flux distribution on the longitudinal end face of the rotor.Through the analysis of the Fourier series，the concave profile end tooth structure considering the reverse phase compensation principle is put forward.The structure can eliminate the odd harmonic wave of the normal and thrust force fluctuations.It can also overcome the shortcomings of the traditional methods which lead to the motor’s longitudinal pitching movement trend by optimizing rotor length to reduce the thrust fluctuation.The rotor’s lateral pitching movement trend can be eliminated by the structure too.In the end，A 12 slots 11 poles PMLM with weaker slot effect is taken for example.The finite element simulation and experiment are employed，and the results show that the method can reduce the normal and thrust ripples of the end effect force.

Permanent magnet linear motor (PMLM)，end effect，normal component of the end effect force，thrust component of the end effect force，concave profile end-tooth

國家自然科學(xué)基金(51377108)，遼寧省高等學(xué)校創(chuàng)新團(tuán)隊(duì)項(xiàng)目(LT2013006)和國家科技重大專項(xiàng)子課題(2012ZX04001-011-003)資助項(xiàng)目。

2014-12-22 改稿日期2015-02-01

TM351

彭 兵 男，1975年生，博士，副教授，研究方向?yàn)橛来潘欧姍C(jī)的設(shè)計(jì)與控制。(通信作者)

劉鐵法 男，1992年生，碩士研究生，研究方向?yàn)橛来潘欧姍C(jī)的設(shè)計(jì)與控制。