整體雙錐形環件閉式徑向輾軋毛坯尺寸的設計方法

李蘭云，李 霄，劉 靜，谷瑞杰，何 志

(1.西安石油大學材料科學與工程學院材料加工重點實驗室，陜西 西安 710065;2.汽車零部件先進制造技術教育部重點實驗室(重慶理工大學)，重慶 400054;3.華中科技大學材料成形與模具技術國家重點實驗室，湖北 武漢 430074;4.中國重型機械研究院股份公司，陜西 西安 710032;5.金屬擠壓/鍛造裝備技術國家重點實驗室，陜西 西安 710032)

0 前言

環件輾軋作為精確塑性成形研究前沿領域的一個重要方向，具有省力、節能、節材、效率高、成本低、產品性能好等顯著優點，是目前世界各國石油化工、能源機械和航空航天等高技術領域中的環類零件成形制造實現輕量化、精確化、柔性化、高性能、低成本和短周期的重要途徑［1，2］。環件輾軋通常分為徑向輾軋和徑軸向輾軋兩種，均是利用軋輥的旋轉驅動和直線進給作用使毛坯連續咬入軋制孔型，產生壁厚減薄、直徑增大、截面輪廓成形的連續局部塑性變形，進而直接獲得復雜截面輪廓形狀的環類產品［3，4］。然而，在環件輾軋成形工藝過程中由于同時存在直徑擴大運動和復雜截面形成，因此研究毛坯尺寸設計方法以合理分配不均勻變形量，這不僅是實現環件輾軋順利開展并穩定進行的前提條件，而且在獲得具有精確形狀尺寸和精準組織性能的高性能環件方面具有重要作用［5，6］。

迄今為止，國內外學者對環件輾軋毛坯設計進行了一些簡單研究。在環件徑向輾軋毛坯設計方面，Qian 等分別研究了T 形截面環件［7］和臺階形截面環件［8］輾軋毛坯設計優化，但其主要思想是先直接給定不同形狀的毛坯尺寸，然后采用理論解析、試驗或者有限元仿真的方法研究給定毛坯輾軋過程的變形行為，從而實現毛坯形狀的優選。在環件徑軸向輾軋毛坯設計方面，Keeton［9］提出了一個基于毛坯瞬時高度和瞬時壁厚的數學公式來設計矩形截面環件徑軸向輾軋的毛坯，該方法雖可避免成形缺陷，但對于某一個環件輾軋在給定芯輥直徑的前提下只能設計出唯一的毛坯，且這個毛坯也不一定是最優的;Kang等［10］提出了基于剛塑性有限元法的反向模擬方法用于環件輾軋的毛坯尺寸設計，但由于環件輾軋過程的幾何、邊界和物理三重非線性導致其計算效率不高;郭良剛等［11］針對矩形截面環件徑軸向輾軋的三種變形形式，提出了一種毛坯尺寸設計方法，但該方法無法推廣到異形截面環件輾軋毛坯設計中。

然而，近年來各種異形截面環件的需求量不斷增加、品種越來越多、尺寸越來越大、所用材料種類也日益呈現多樣化，這些都需要更為先進的毛坯設計技術與之相適應。整體雙錐形環件是一種典型的異形截面環件，被廣泛應用于石油、化工、風電、航空、航天、汽車、軸承等工業領域中［12］。因此，本文將以整體雙錐形環件閉式徑向輾軋為例，研究一種基于輾軋比的毛坯尺寸設計新方法，以期為異形環件輾軋毛坯尺寸設計提供一種新的思路和借鑒。

1 基于體積不變原理確定毛坯尺寸計算公式

1.1 毛坯結構設計

假設最終成形的環件為如圖1a 所示的整體雙錐形環件，其中RRL、RRM、RRS、HR、α 分別表示整體雙錐形環件的外半徑、端面半徑、內半徑、軸向高度和錐形角。VR和SR分別為整體雙錐形環件的體積和截面積。

因整體雙錐形環件是一種較為復雜的異形環件，若直接采用矩形截面毛坯則輾軋成形過程中金屬流動異常復雜，各項工藝參數較難設計和控制，且輾軋成形的產品的精度和性能均難以滿足設計要求。為有效避免這一問題，本文選用如圖1b 所示的雙錐形截面毛坯，其中RBL、RBM、RBS、HB分別表示雙錐形截面毛坯的外半徑、端面半徑、內半徑和軸向高度。采用這種形狀毛坯的最大特點是使得雙錐形截面毛坯的錐形角等于整體雙錐形環件的錐形角，從而可以減少徑向輾軋過程的復雜度。VB和SB分別為雙錐形截面毛坯的體積和截面積。

基于整體雙錐形環件和所設計的雙錐形截面毛坯的結構，根據閉式徑向輾軋的原理設計出的芯輥如圖1c 所示，其中RML和RMS分別為芯輥的大端外半徑和小端外半徑。另外，這種芯輥的軸向高度也等于HR，且錐形角也等于整體雙錐形環件的錐形角。

1.2 確定毛坯尺寸設計公式

根據塑性成形中的體積不變原理有

同時根據輾軋比λ為輾軋前毛坯截面積與輾軋后環件截面積之比的定義有

由圖1b 可知:

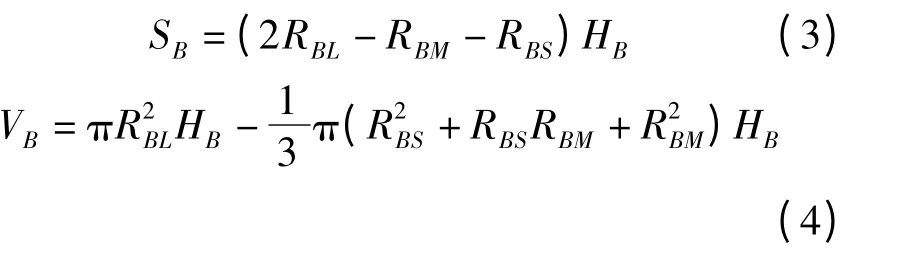
同時還可以得到

圖1 環件、毛坯和芯輥示意圖Fig.1 Schematic diagram of ring part，ring blank and mandrel

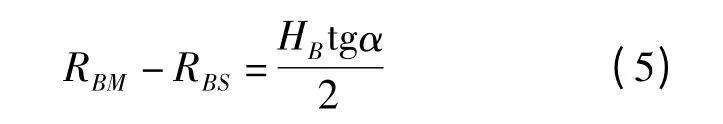
將式(2)、(5)代入式(3)中可得

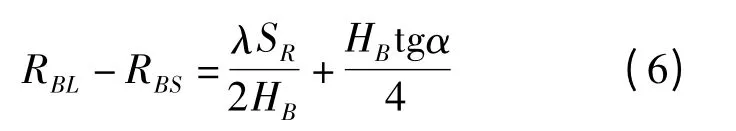
再將式(1)和式(5)代入式(4)中可得

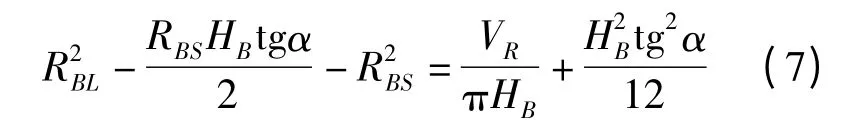
由于選用的成形方式為閉式徑向輾軋，故有

將式(8)代入式(6)和式(7)，則

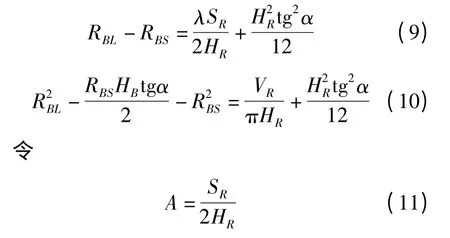
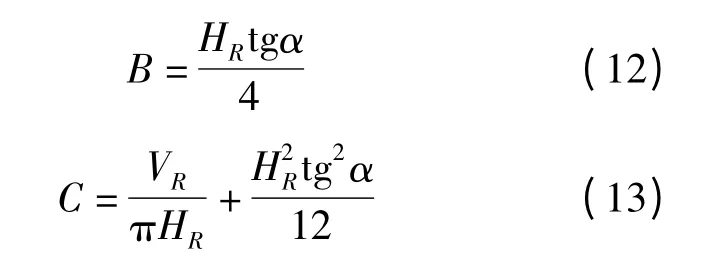
則式(9)和式(10)變為

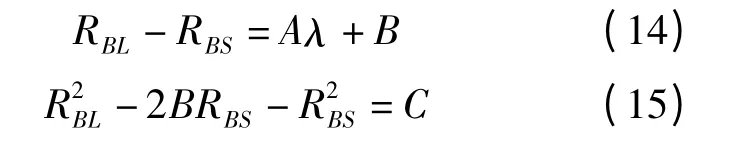
聯立式(14)和式(15)求解可得:

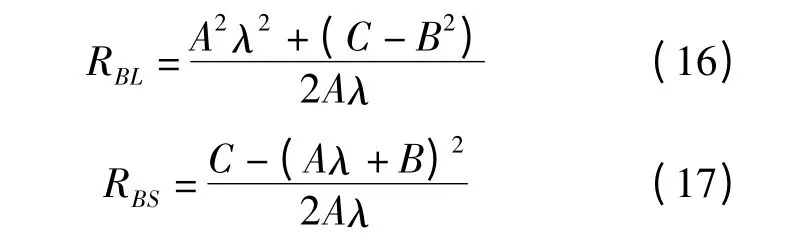
再將式(12)和式(17)代入式(5)中可得:

因此，整體雙錐形毛坯的外半徑RBL、端面半徑RBM、內半徑RBS和軸向高度HB分別按式(16)、式(18)、式(17)和式(8)進行確定，而其中A、B、C 的值由式(11)～式(13)確定。

2 基于穩定成形條件確定輾軋比的取值范圍

根據環件輾軋成形原理，為使整個整體雙錐形環件閉式徑向輾軋成形過程能順利地開展并穩定地進行，需滿足如下三項基本條件:

(1)條件1。輾軋比必須大于1，即

(2)條件2。在環件徑向輾軋過程中，芯輥朝驅動輥的連續進給使得環件的壁厚不斷減薄、半徑不斷長大、截面輪廓逐漸成形。因此毛坯的壁厚應大于環件的徑向壁厚，且毛坯的半徑應分別小于環件的半徑。即

(3)條件3。毛坯的半徑必須大于芯輥的半徑，這樣才能保證將芯輥放入毛坯內。即

根據條件1 中直接給出的輾軋比的取值范圍，依次考慮條件2 和條件3 來獲得輾軋比取值范圍。

2.1 考慮條件2 的輾軋比取值范圍

(1)由WBL＞WRL得

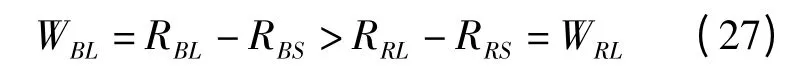
將式(14)代入式(27)后有

(2)WBS＞WRS得

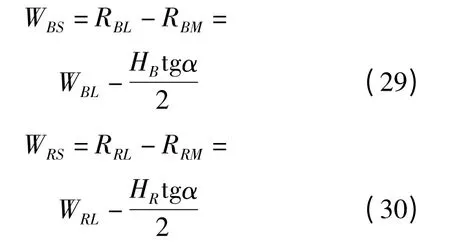
由于HB=HR，故只要當WBL＞WRL滿足時，WBS＞WRS也就自動滿足了。

(3)RBS＜RRS。將式(17)代入式(22)中有

變形后有

A2λ2+2A(B+RRS)λ+(B2－C)＞0 (32)由式(11)～式(13)可知A、B、C 均大于0，進而可知總是成立的，故

(4)RBM＜RRM。

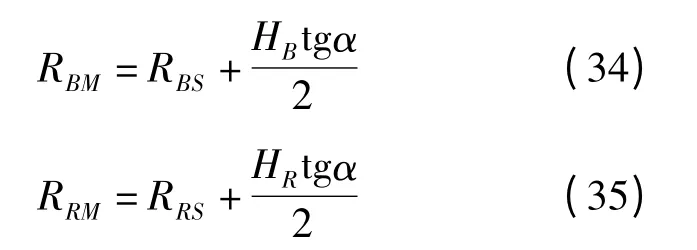
由于HB=HR，故只要當RBS＜RRS滿足時，RBM＜RRM也就自動滿足了。

(5)RBL＜RRL。將式(16)代入式(24)中有

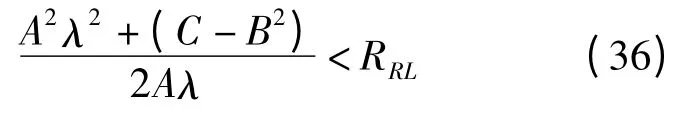
變形后有

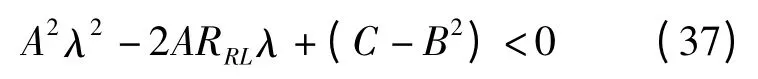
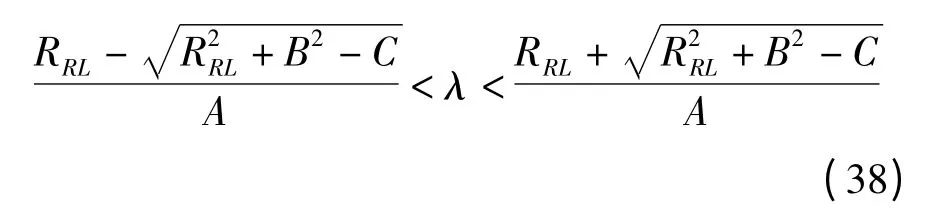
2.2 考慮條件3 的輾軋比取值范圍

(1)RBS＞RMS。將式(17)代入式(25)中有

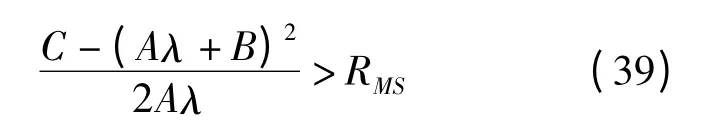
變形后有

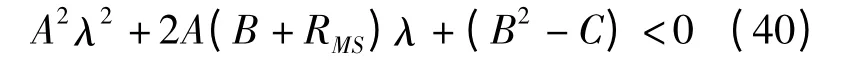
因為Δ40=4A2(R2MS+2BRMS+C)＞0 總是成立的，故由式(40)可得

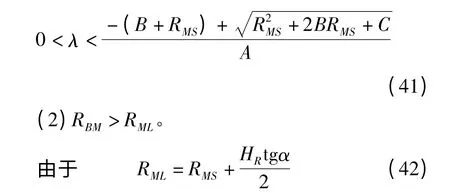
只要當RBS＞RMS滿足時，所以RBM＞RML也就自動滿足了。

2.3 綜合確定輾軋比的取值范圍

最后，綜合考慮上述條件，由圖1 得

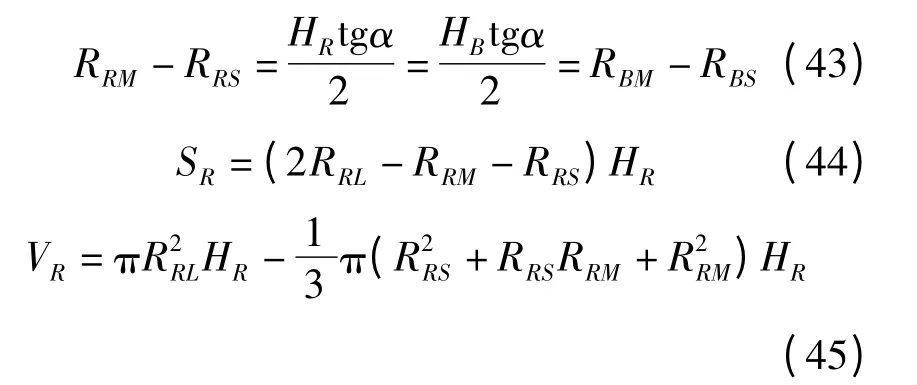
同時結合A、B、C 定義可以推導得

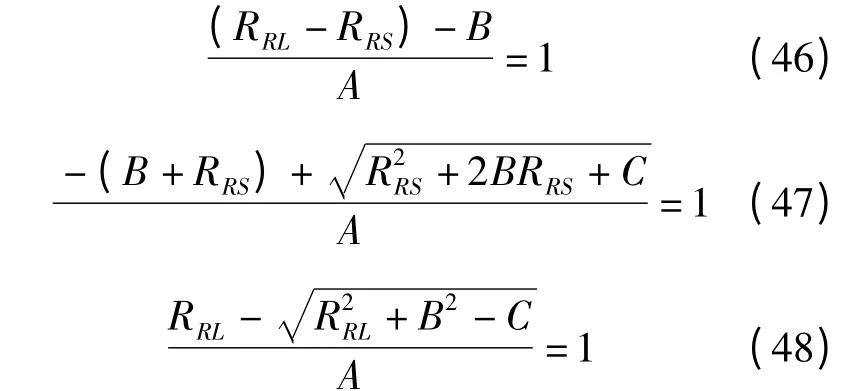
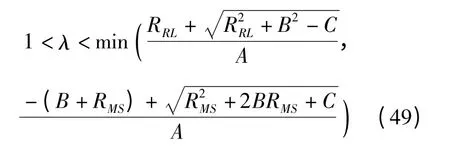
3 基于輾軋比的毛坯尺寸設計新方法

在給定如圖1a 所示的整體雙錐形環件尺寸(具體包括:外半徑RRL、端面半徑RRM、內半徑RRS、軸向高度HR和錐形角α)的條件下，本文提出了一種基于輾軋比的雙錐形截面毛坯尺寸設計新方法，其具體步驟為

(1)確定整體雙錐形環件閉式徑向輾軋過程中的初始毛坯為如圖1b 所示的雙錐形截面毛坯;

(2)確定出如圖1c 所示的芯輥的大端外半徑RML和小端外半徑RMS取值;

(3)按式(45)和式(44)分別計算出整體雙錐形環件的體積VR和截面積SR;

(4)按式(49)計算出整體雙錐形環件閉式徑向輾軋成形過程中輾軋比λ 的合理取值范圍;

(5)在所計算出的輾軋比λ 的合理取值范圍內任意選擇一個λ 值;

(6)將上述取值代入到式(16)、式(18)、式(17)和式(8)中就可分別計算出雙錐形截面毛坯的外半徑RBL、端面半徑RBM、內半徑RBS和軸向高度HB;

根據上述過程可知:若選擇輾軋比λ 取值不同，則計算得到的雙錐形截面毛坯尺寸取值也不同;但是這些尺寸取值都是符合設計要求的。因此，可見所提出方法特點是:只需獲得最終整體雙錐形截面環件的幾何尺寸以及芯輥的外半徑，就可以快速確定出輾軋比λ 的取值范圍;然后結合在確定的輾軋比λ 范圍內所選取的輾軋比λ 值就可以快速確定雙錐形截面毛坯尺寸。

4 設計實例

若最終整體雙錐形環件的外半徑RRL為90 mm、端面半徑RRM為85 mm、內半徑RRS為75 mm、軸向高度HR為30 mm。并假設芯輥小端外半徑RMS為35 mm。

根據給定的整體雙錐形環件尺寸可計算出其截面積SR=600 mm2和體積VR=159355 mm3，可計算出輾軋比λ 合理取值范圍為［1.00，1.74］。因此，輾軋比λ 可在［1.00，1.74］取任何一個值。最后，選取一個輾軋比λ 值，就可計算出雙錐形截面毛坯的外半徑RBL、端面半徑RBM、內半徑RBS和軸向高度HB。表1 給出了選取七個不同輾軋比λ 值計算得到的雙錐形截面毛坯尺寸。該方法針對同一尺寸的整體雙錐形環件產品，能夠設計出一系列不同尺寸的雙錐形截面毛坯，這為研究整體雙錐形環件閉式徑向輾軋的不均勻塑性變形機理和形性一體化協同調控提供了重要基礎。

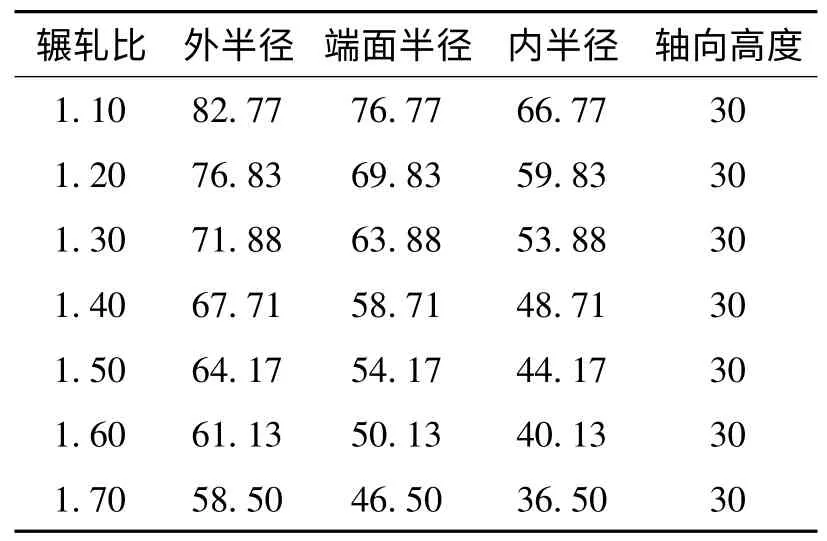
表1 基于不同輾軋比的雙錐形截面毛坯尺寸Tab.1 BCSB dimensions based on different rolling ratios mm

最后，將所提出的整體雙錐形環件閉式徑向輾軋毛坯尺寸設計思想擴展到了其它18 種異形截面環件徑向輾軋毛坯尺寸設計中，并通過虛擬輾軋試驗驗證了其可行性和有效性。在上述研究的基礎上，利用C 語言設計和開發一套如圖2 所示的異形環件徑向輾軋毛坯尺寸設計軟件，并已成功獲批軟件著作權。

圖2 異形環件徑向輾軋毛坯尺寸設計軟件Fig.2 Software of blank dimensions design for radial profile ring rolling

5 結論

針對整體雙錐形環件閉式徑向輾軋毛坯尺寸設計這一實際問題，利用體積不變原理給出了雙錐形截面毛坯尺寸的計算公式，根據穩定成形條件推導了輾軋比的合理取值范圍，提出了一種基于輾軋比的毛坯尺寸設計新方法和軟件系統，并通過實例驗證了所提方法的有效性和可行性。當然還需指出的是，毛坯尺寸設計與工藝參數設計是緊密相關的，只有它們都進行了合理設計且符合輾軋機實際力能參數，才能成形出符合實際的環件產品。

［1］Lanyun Li，He Yang，Lianggang Guo.Hot shape rolling［J］.Comprehensive Materials Processing，2014，5(19):393－439.

［2］Lanyun Li，He Yang，Lianggang Guo，Zhichao Sun.Research on the influences of material properties and forming parameters in T-shaped closed cold ring rolling process International Journal of Materials and Product Technology，2010，38(2－3):323－326.

［3］華林，黃興高，朱春東.環件軋制理論和技術［M］.北京:機械工業出版社，2001.

［4］華林，錢東升.軸承環軋制成形理論和技術［J］.機械工程學報，2014，50(16):70－76.

［5］Lanyun Li，Xiao Li，Jing Liu，Zhi He.Modeling and simulation of cold rolling process for double groove ball-section ring［J］.International Journal of Advanced Manufacturing Technology，2013，69(5－8):1717－1729.

［6］Lanyun Li，Xiao Li，Zhi He.Research on the effect of geometric parameters of ring blank on cold profiled ring rolling process［J］.International Journal of Materialsand Product Technology，2011，42 (3－ 4):195－208.

［7］Dongsheng Qian，Lin Hua，L.B.Pan.Blank design optimization for T-section ring rolling［J］.Ironmaking＆ Steelmaking，2009，36(6):462－469.

［8］Dongsheng Qian，Lin Hua.Blank design optimization for stepped-section profile ring rolling［J］.Science China Technological Sciences，2010，53(6):1612－1619.

［9］Keeton C R.Ring rolling in Metals handbook:Forming and forging［M］.Metals Park，OH:ASM International，1988.

［10］Kang B S，Kobayashi S.Preform design in ring rolling processes by the three-dimensional finite element method［J］.International Journal of Machine Tools and Manufacture，1991，31(1):139－151.

［11］郭良剛，楊合，金堅誠.環件徑軸向軋制毛坯尺寸設計方法［J］.機械工程學報，2010，46(24):1－9.

［12］Lanyun Li，He Yang，Lianggang Guo，Zhichao Sun.A control method of guide rolls in 3D-FE simulation of ring rolling［J］.Journal of Material Processing Technology，2008，205(1－3):99－110.