借力數學直覺，讓思維綻放精彩

江蘇蘇州高新區獅山實驗小學校（215001） 張曉芳

在教學中，學生在解決問題時常常不經過邏輯思維過程，瞎猜亂說，但事實上，學生是在利用直覺解決問題，這種直覺也是一種有效的數學思維，被人們稱之為直覺思維。直覺思維和邏輯思維一樣，是發展數學能力的有效思維，只是由于傳統教學模式過分注重邏輯思維，抑制了直覺思維的發展。那么，該如何借助稍縱即逝的直覺，推動學生直覺思維的發展呢？筆者現結合自己的教學實踐，談談體會。

一、抓住錯覺，突破誤區

直覺思維的表現形式通常為一閃念，稍縱即逝，具有突發性和跳躍性，實際教學中通常會出現在思維活躍的學生身上。但教學中教師往往會將這種直覺當做學生的瞎說亂說，從而錯過良好的教學時機，影響了學生直覺思維的培養。那么，如何才能捕捉學生的直覺并善加利用呢？有經驗的教師往往會關注學生的第一反應，而第一反應通常是一種錯覺，教師會根據學生的這種直觀錯覺進行教學設計，從而突破學生的思維誤區，一舉擊破教學難點。

例如，在教學蘇教版內容“三角形的三邊關系”時，教學的難點是讓學生理解“任意兩邊之和大于第三邊”。筆者先讓學生動手做任意三角形，學生采用拼擺、剪貼、折紙的方式展開操作，此時設置問題：如果給你任意三根小棒，你都能拼成一個三角形嗎？學生異口同聲地認為一定能。全班學生的第一反應是個明顯的錯誤，根據這一錯誤的直覺，筆者設計了操作活動，給每個學生準備了三根小棒（a＋b＜c），學生經過操作后發現，居然沒有一組能圍成三角形。到底為什么呢？學生由此產生了強烈的求知意愿，在突破思維誤區之后展開課堂探究，有效促進了學生思維的發展。

二、加強引導，激活直覺

在小學數學教學實踐中，有這樣一個基本事實，那就是學生的很多知識都是在默認的基礎上展開學習的。如在小學一年級時，認識正方形、長方形、圓等圖形的特點，對于學生來說，并不是第一次接觸這些圖形，因而在長期的觀察和感悟中，學生對這些圖形的特性早就擁有一種無須證明就能夠知曉的直覺，到了高年級再進行數學探究時，這種直覺就會被激活，能夠幫助學生瞬間領悟概念的本質，并作出有效的數學判斷。在數學教學中，教師要加強猜想、聯想、觀察等思維引導，以此激活學生的直覺思維。

例如，在教學“循環小數”這一內容時，筆者先向學生揭示主題之后，展開猜想引導，讓學生根據自己的理解，先來猜測一下循環小數是什么。學生認為，首先應該是小數，其次小數點后的數字會有很多；再次，小數點后的數字會有反復，不停重復出現；還有學生補充認為，有可能小數點后的數字會是單個重復，如“1111…”，還有可能小數點后的數字會有多個重復，如“123123123…”。

以上教學，教師先從猜想入手，讓學生對循環小數的數學概念進行初步感知，從而激活學生對循環小數這個概念的直覺思維，有效避免了教師的生硬說教，為下一步理解小數的意義奠定了良好的基礎。

三、整合互補，完善直覺

在數學領域，直覺思維和邏輯思維相比，具有不可捉摸性，因而只能作為數學證明的補充，而不能成為數學思維的主體。在小學數學教學中，教師不能任由學生瞎猜亂猜，更不能過分推崇直覺，而是要保護學生的直覺思維，將直覺思維和邏輯思維整合互補，使兩者相輔相成，促進直覺思維的完善。

例如，在教學蘇教版四年級內容“三角形”時，有這樣一道題目：在兩條平行線間畫三角形（如圖1），兩個三角形的高有什么關系？學生的第一個直覺反應就是認為兩個三角形的高相等，但如何證明呢？為此，筆者展開引導，學生經過探究后發現，曾經在三年級時學過這樣一個數學定理：即兩條平行線間的距離是相等的。通過這樣的邏輯推理，學生讓稍縱即逝的直覺得到了邏輯還原，能夠將難以捉摸的直覺思維轉化為有理有據的邏輯思維，從而促進學生直覺思維的完善和發展。

伊思·斯圖爾特曾經指出，數學教學的本質是直覺和嚴格的邏輯秩序巧妙融合，讓靈感呈現邏輯的力量，這也正是數學的魅力所在。在小學數學教學中，學生的直覺閃現是一個不可忽視的有效資源，作為教育工作者，應該充分發揮直覺的優勢，幫助學生發展直覺思維，提高數學思維能力。

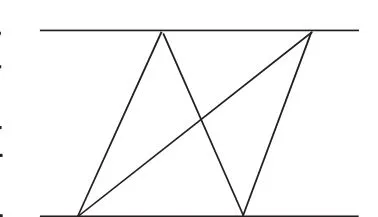
圖1