采用區間分析的加速退化試驗評估方法

劉樂，李曉陽 ，姜同敏

(1.北京航空航天大學 可靠性與系統工程學院，北京100191; 2.可靠性與環境工程技術重點實驗室，北京100191)

現代工業對產品的長壽命高可靠性有不斷增長的需求，為了考核該類產品的壽命與可靠性水平，在產品正式投產之前需開展加速試驗.加速試驗技術采用嚴酷于產品正常使用的環境條件，加速產品失效或退化過程，從而在短時間內獲取壽命或退化數據進行可靠性和壽命評估［1］.與壽命數據相比，退化數據包含更多的產品性能變化信息，因此加速退化試驗(ADT)技術得到了較多的關注［2-3］.

然而，傳統的加速退化試驗數據評估方法假設采集到的退化數據是精確數據，該假設可能與一些實際情況存在不符，這些不符來源于:①測量設備的容差;②不同測試人員對同一數據的認知;③數據的缺失等.因此，在實際試驗中可能獲取到的是區間型退化數據.若只對其進行簡單的均值處理，則忽略了其蘊含的隨機與認知不確定性，那么就會給出不合理的壽命和可靠性評估結果.若能采用區間型數據分析方法，通過敏感性分析定量給出認知不確定性對評估結果的影響，最大程度地保證評估結果的可信性，為消除測量的認知不確定性或評價決策風險提供依據.

在考慮非精確數據方面，文獻［4］研究了競爭失效狀態下的產品可靠性分析方法，采用模糊方法的隸屬函數來刻畫區間型退化數據.文獻［5］采用模糊回歸方法對退化過程進行建模，該模型假設退化數據是精確的，而采用非精確模型參數來表征退化建模的不確定性.通常來說，非精確退化數據可以表征為區間型，采用區間運算來加以處理［6］.文獻［7］給出一種精確輸入和區間輸出的區間回歸方法，將最小二乘的中心趨勢特性和模糊回歸的可能性特性結合到二次規劃問題中，給出兩類特性模型的優化結果.文獻［8］采用區間分析方法研究了線彈性斷裂力學中應力強度因子的不確定性問題，結果表明該方法優于傳統的概率分析方法.在加速試驗領域，文獻［9-10］指出在加速試驗中除系統自身的隨機不確定性外還存在大量的認知不確定性，需要采用適當的建模方法來評估其對系統安全和壽命預測的影響.因此，本文針對加速退化測量中存在的認知不確定性問題，采用區間回歸方法來建模分析，研究測量認知不確定性對可靠性和壽命評估結果的影響.

由于加速退化數據測量中，不僅存在系統的隨機不確定性，還有人的參與引起的認知不確定性.本文針對該情況，重點考慮認知不確定性的影響，解決區間型加速退化試驗數據的壽命和可靠性評估問題.本文首先介紹所采用的模型及區間分析方法;其次研究了基于區間分析方法的加速試驗數據分析方法;最后通過數值案例驗證所提方法，并分析認知不確定性的影響.

1 退化模型及區間分析方法

1.1 退化模型

隨機過程具有較好的物理和統計特性，廣泛用于描述產品的性能變化過程［11］.其中，維納(Wiener)過程常用于加速退化試驗評估［12-14］，文獻［15］給出了一種通用維納過程模型，該模型能夠泛化成各類常用的維納過程模型.本文取產品退化性能參數X(t)的模型形式為

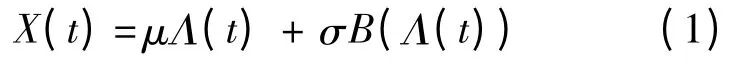
若初始退化值X(0)不為0，則X(t)= X(t)－X(0).式中:σ 為擴散系數;B(·)為標準布朗運動;Λ(t)為關于時間t 的非減函數，即時間尺度變換，常見變換方式有指數、對數、冪;μ 為漂移系數，通常假設其與應力條件服從對數線性關系(如溫度應力下的Arrhenius 模型，電應力下的Eyring 模型等［16］)，如下:

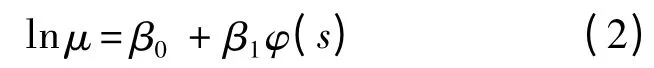
式中:φ(s)為應力相關的函數;β0和β1為常數.

根據維納過程特性可知，退化增量滿足

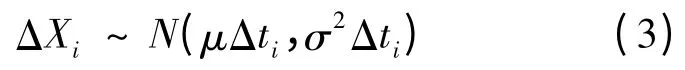
式中:ΔXi= X(ti)－ X(ti－1);Δti= Λ(ti)－Λ(ti－1).

當失效閾值為C 時，產品首次穿過該閾值的時間T(首穿時)服從變換后的逆高斯分布［17］，即Λ(T)～IG(C/μ，C2/σ2)，其中IG(b1，b2)的概率密度函數為(b1＞0 為均值，b2＞0 為形狀參數)

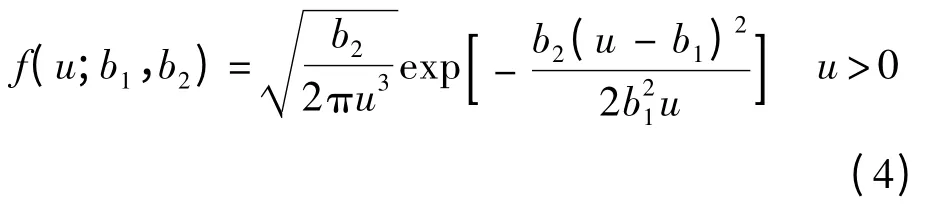
進而推導產品的可靠度函數和可靠壽命為

式中:－1表示函數取反;r 為規定的可靠度值.

1.2 區間回歸分析

區間分析方法是回歸分析方法的一種，通過假設區間回歸系數來獲取自變量和因變量之間的關系，常見的有區間輸入-區間輸出、精確輸入-區間輸出.考慮到工程實際中，測量時間或加速應力為精確的，本文采用精確輸入-區間輸出的線性回歸分析方法進行建模，得到模型參數(即區間回歸系數).模型為

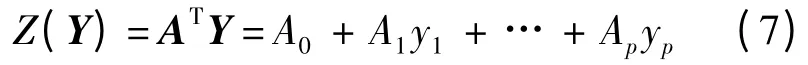
式中:Y=［1，y1，…，yp］T為輸入向量，p 為模型輸出參數種類數;A =［A0，A1，…，Ap］T為區間型回歸系數，Ai=〈ai，ci〉，ai和ci分別表示回歸系數Ai的中心值和半徑.根據區間運算法則，式(7)可轉換為

式中:a =［a0，a1，…，ap］T;c =［c0，c1，…，cp］T;yj=［1，yj1，…，yjp］T.

區間分析方法主要分為兩類:基于可能性概念的可能回歸分析(可能性模型)和基于最小化誤差的最小二乘方法(必要性模型)［7］.兩類模型分別為

通常假設兩類模型具有相同的中心值，即兩類模型的回歸系數為和A*i=〈ai，ci〉，則兩類模型求解可分別轉化為二次規劃問題，即

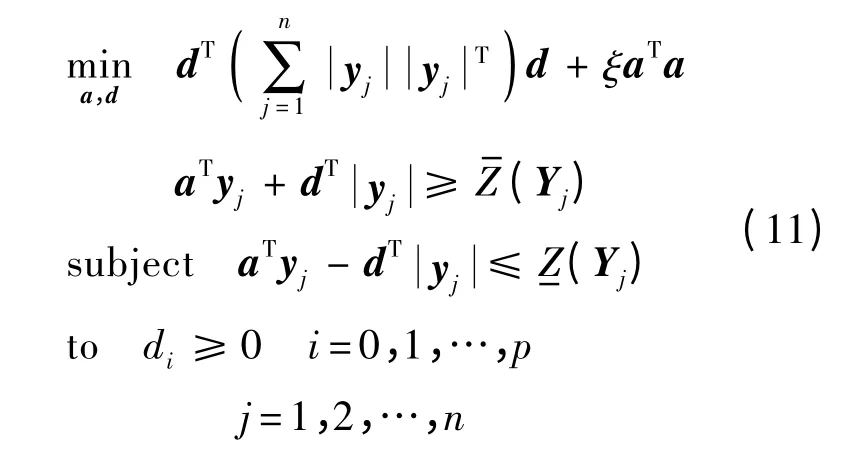
和

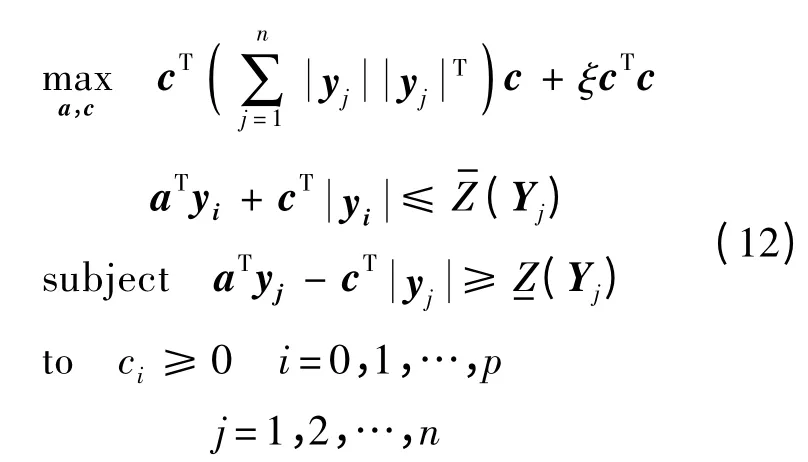
對于實際觀測區間變量Z(Y)滿足條件

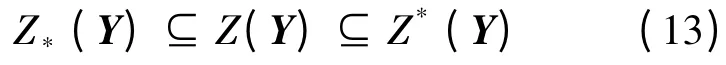
上述二次規劃模型能夠處理區間型數據，對式(1)取期望可知E(X(t))=μΛ(t)，對于精確輸入Λ(t)-區間輸出，采用區間回歸方法，能夠獲取區間回歸系數，即漂移系數μ.

2 區間型加速退化試驗分析

2.1 基于區間回歸分析方法的加速退化建模

考慮到測量、人為等因素，退化數據是非精確的，采用區間型描述比精確數據更為合適.而對于精確輸入-區間輸出型數據，采用兩類模型進行建模分析，獲取區間型結果.關于兩類模型，可能性模型是對模型輸入輸出之間可能性的一種表征，其輸出最大程度覆蓋所有的實際觀測區間.必要性模型是對模型輸入輸出之間集中程度的一種表征，其輸出最大程度包含于實際觀測區間，即滿足模型關系式(13).

在時間尺度上，即精確時間-區間退化數據，本文采用可能性模型最大可能地獲取漂移系數的區間值.而在應力尺度上，即精確應力-區間漂移系數，在漂移系數外推的過程中需要在所有可能結果中找到最大程度符合加速模型的結果，即中心趨勢特性，而必要性模型能夠表征此特性，為此本文采用必要性模型進行外推.具體建模評估流程如圖1 所示.

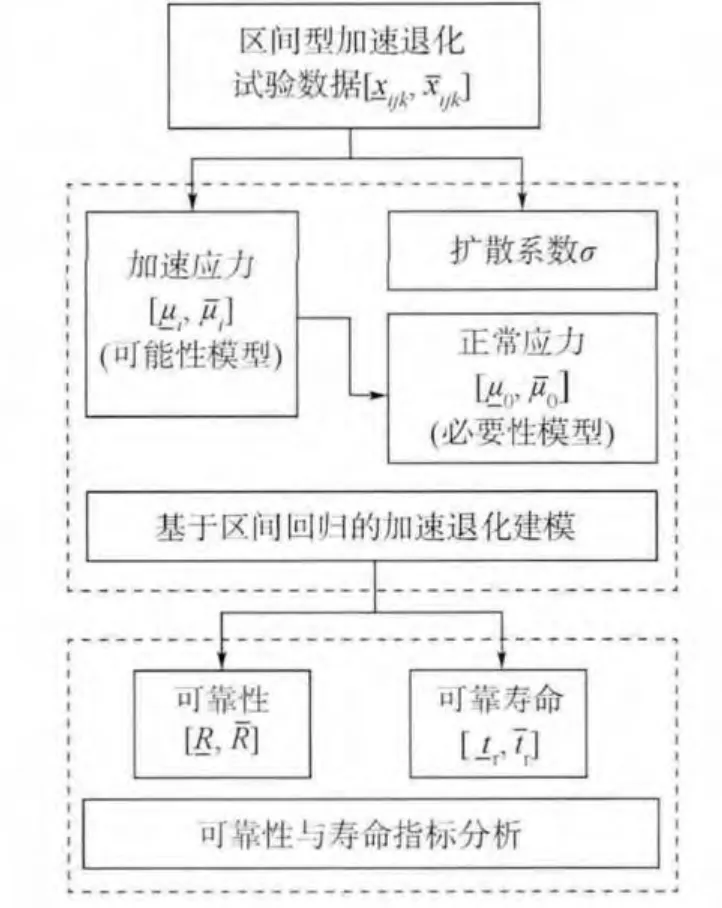
圖1 區間型加速退化試驗分析流程Fig.1 Flowchart of interval accelerated degradation testing analysis

本文基于維納過程對退化過程建模，其期望退化路徑服從一元線性過程，因此針對區間型加速退化數據，可采用式(7)進行區間運算(p =1).同時，為了更全面地獲取漂移系數的所有可能取值，采用可能性模型式(11)優化求解，得到的回歸系數A1的區間，即該應力條件下的漂移系數.

對于擴散系數σ，其表征退化過程的隨機特性，通常刻畫一系列隨機因素對產品性能的影響，是與應力和時間無關的常量，為此假設其為精確值.由式(3)可得傳統精確數據下的擴散系數σ 為

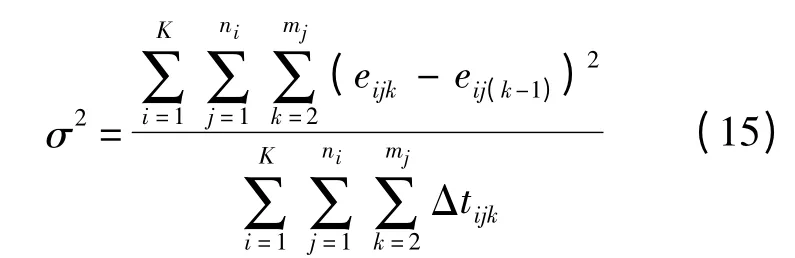
式中:eijk為此監測點的預測相對誤差，即eijk=xijk－μijkΛ(tijk).當退化數據為區間型時，相對誤差同時存在于預測上限和下限，為此取上下限誤差的平方和根作為此監測點的預測誤差，即

將式(16)替換至式(15)得到擴散系數σ.

為了考核產品的可靠性和壽命指標，需要將加速應力條件下的性能參數外推至正常應力條件下，即通過加速模型式(2)來實現.在步驟1)中獲得應力條件i 下的漂移系數，表示該條件下漂移系數的所有可能結果，則為

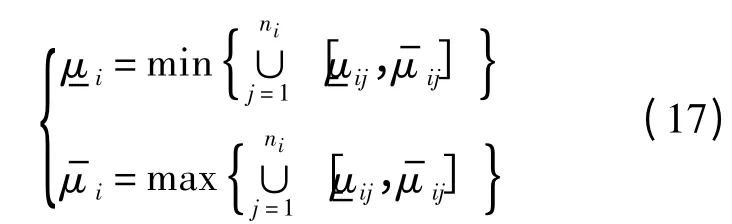
2.2 可靠性與壽命指標分析

傳統的精確退化數據評估，給出產品正常使用條件下的壽命和可靠度指標，式(5)和式(6)基于維納過程給出首穿時服從逆高斯分布的可靠度和壽命函數.在第2.1 節給出了基于區間分析方法的加速退化試驗建模方法，得到區間漂移系數和擴散系數σ.

根據逆高斯分布性質可知，可靠度和壽命指標區間為

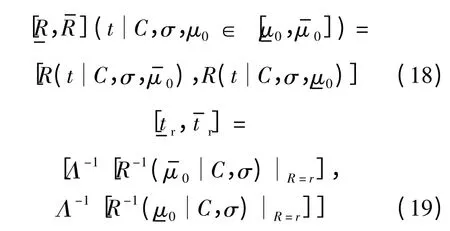
上述建模分析方法能夠處理區間型加速退化試驗數據，基于式(18)和式(19)分析測量過程中存在的認知不確定性對可靠性和壽命評估結果的影響，進而為消除加速試驗中的認知不確定性、提高評估結果可信度提供依據.

3 數值案例

3.1 加速退化試驗信息

為了驗證本文方法的有效性及分析測量不確定性對可靠性和壽命評估結果的影響.選用文獻［18］提供的恒定應力加速退化試驗數據，試驗為了測試某種金屬合金的耐磨性，在不同加載條件下進行滑動測試，記錄劃痕寬度用于分析確定載荷的影響，具體試驗信息見表1，原始數據見圖2.

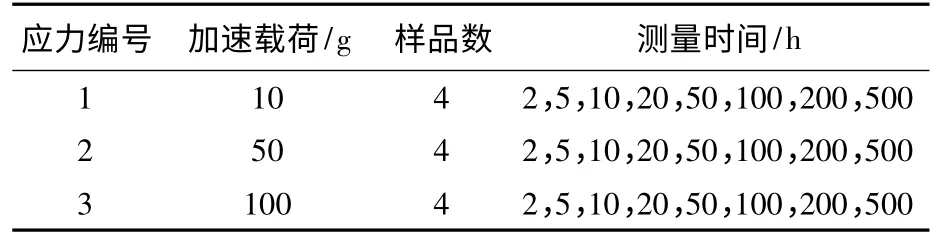
表1 金屬合金的加速磨損退化試驗信息Table 1 Information on accelerated wear degradation testing for metal alloy

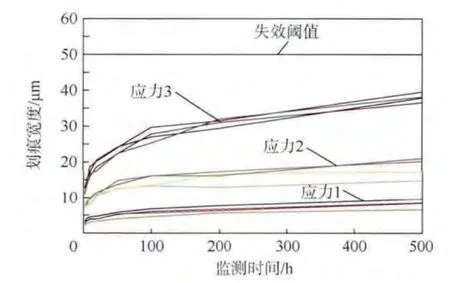
圖2 3 種加載條件下的加速磨損退化試驗數據Fig.2 Degradation data for accelerated wear testing under three applied weights

假設數據記錄過程，由于人的認知等主觀因素，如多名檢測人員，使得記錄數據是非精確的，為了刻畫此類認知不確定性，本文在原始數據的基礎上進行如下處理:

1)隨機從正態分布中抽取Δi滿足:Δi～N(m，ζm)，m 為均值，ζ 為收縮系數.簡單起見，設ζ=0.02 表示多人參與情況，ζ =0 表示單人參與情況.

2)第i 個原始測量值± |Δi|作為該測量點的實際記錄值，即區間退化數據.

這里，可以看出m 參數反映的是測量不確定性的程度，m 值越大表示不確定性程度越高，通過提高檢測人員水平、設備精度等措施來加以降低或消除，因此本文取不同的m 值來分析退化數據的測量不確定性對評估結果的影響.

已知失效閾值C=50 μm，假設其正常使用條件下的加載為5 g，退化過程服從維納過程，加速模型式(2)中φ(s)=W(W 為施加的加速應力載荷)，Λ(t)=ln t，首先，取m=0.5 μm，利用本文方法進行可靠性和壽命評估.然后，根據第2.1 節區間型加速退化數據的建模方法，得出各加速載荷條件下的漂移系數及擴散系數σ =0.677 2.根據加速模型式(2)將代入通用模型式(14)，結果見圖3，外推正常載荷下的漂移系數(必要性模型)為［0.784 4，0.938 6］.最后，將所得參數結果代入式(18)和式(19)，得到的可靠度區間如圖4 所示，可靠度為0.9 的壽命為exp(46.72，55.19)h.

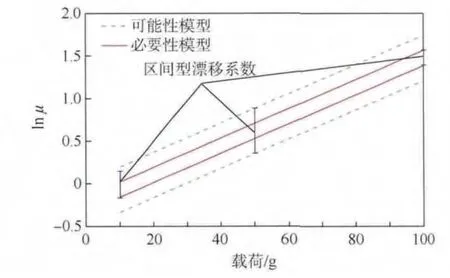
圖3 3 種加載條件下的漂移系數μFig.3 Draft coefficient μ under three applied weights

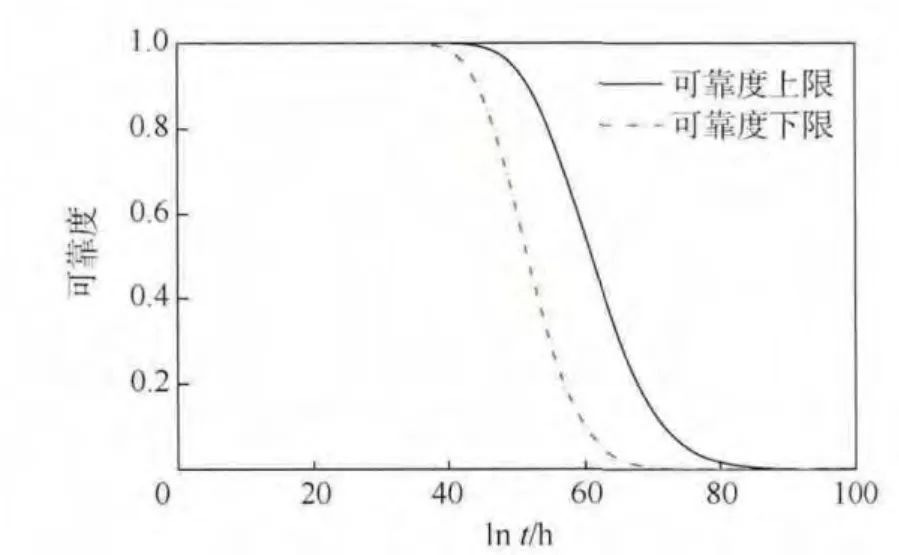
圖4 當m=0.5 μm 時的區間可靠度曲線Fig.4 Interval reliability curves when m=0.5 μm

3.2 測量不確定性對可靠性和壽命的影響分析

測量不確定性主要分為兩類:認知不確定性和隨機不確定性，其中隨機不確定性來源于系統誤差，無法避免和消除;然而認知不確定性來源于人的主觀原因，是可以采取措施(如增大樣本量來增強認知水平)來消除或轉化為隨機不確定性.

為了分析該類不確定性對產品可靠性和壽命結果的影響，設置m 分別取0.01、0.03、0.05、0.07、0.1、0.3、0.5、0.7、1 μm 來分析對應的可靠度和壽命指標情況.這里，本文考慮兩種工程實際情況:

1)多人參與加速試驗測試的情況(認知水平存在不同).

2)單人參與測試的情況(認知水平單一).

為了模擬這兩種情況，根據第3.1 節方法，分別取ζ=0.02 和0 并代入各m 值進行求解.通過兩種情況的對比分析，了解人的參與所引起的認知不確定性對壽命評估結果的影響.圖5 ～圖7分別給出了兩種情況的漂移系數μ0、擴散系數σ和可靠壽命.

由圖5(a)可知，隨著m 值的降低，第1 種情況下的漂移系數中心值從0.86 增大至0.91 左右，而第2 種情況下穩定在0.887 左右，表明該參數值受測量中認知不確定性的影響，可能的解決途徑是減少人員參與.從總的趨勢上來看，圖5(b)中μ0半徑隨m 值降低而減小，意味著提高人的認知水平能夠在一定程度上降低μ0的不確定性.

對于擴散系數σ，該參數刻畫隨機因素對產品性能的影響，從圖6 可以看出該參數對測量不確定性較為敏感，但同時考慮到該參數與受試產品數目有關，因此當樣品量一定時，降低測量的不確定性有利于該參數的確定.

圖5 兩種情況下不同m 值對應的漂移系數中心值和半徑Fig.5 Center and radius of draft coefficients under different m values in two cases

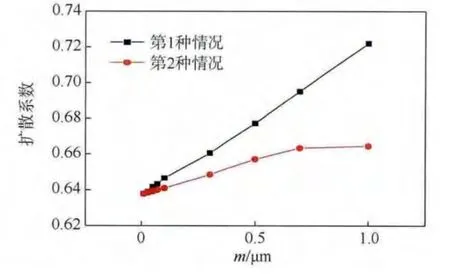
圖6 兩種情況下不同m 值對應的擴散系數Fig.6 Diffusion coefficients under different m values in two cases

圖7 兩種情況下不同m 值對應的可靠度R=0.9 的可靠壽命中心值和半徑Fig.7 Center and radius of reliable lifetimes when R=0.9 under different m values in two cases

對產品而言，實施加速試驗的目的是確定其可靠性和壽命指標，通過給定不同m 值下的μ0和σ 值，代入式(5)和式(6)，結果如圖7(a)和圖7(b)所示，第1 種情況下不同m 值對應的可靠壽命結果存在較大差異，而第2 種情況下結果較為平穩.而對于可靠壽命半徑，兩種情況下都隨著m 值降低而顯著減少，因此為了保證壽命評估結果的合理性，需盡可能消除測量中的認知不確定性，減少人員參與.

4 結 論

本文考慮加速退化數據是非精確情況，采用區間回歸分析方法給出了區間型加速退化試驗數據的可靠性和壽命評估方法.主要結論有:

1)退化數據測量由于人為因素和設備等原因，存在主觀認知不確定性和系統隨機不確定性，在實際加速試驗中應盡量減少人員參與，盡可能地消除測量中存在的認知不確定性.

2)數值案例表明:與壽命評估有關的模型參數，即漂移系數μ0和擴散系數σ 均受測量不確定性的影響，降低不確定性水平能夠使得模型參數更為可信.

3)加速試驗的壽命評估結果受測量不確定性的影響，且隨著認知不確定性的降低，評估結果的不確定性也隨之降低.因此，在試驗過程和結果處理中需考慮和消除此影響.

References)

［1］ Nelson W B.Accelerated testing:Statistical models，test plans，and data analysis［M］.New York:John Wiley ＆ Sons，2009:493-544.

［2］ Meeker W Q，Escobar L A，Lu C J.Accelerated degradation tests:Modeling and analysis［J］.Technometrics，1998，40(2):89-99.

［3］ 鄧愛民，陳循，張春華，等.加速退化試驗技術綜述［J］.兵工學報，2007，28(8):1002-1007.

Deng A M，Chen X，Zhang C H，et al.A comprehensive review of accelerated degradation testing［J］.Acta Armamentarii，2007，28(8):1002-1007(in Chinese).

［4］ Wang Z，Huang H Z，Du L.Reliability analysis on competitive failure processes under fuzzy degradation data［J］.Applied Soft Computing，2011，11(3):2964-2973.

［5］ Gonzalez-Gonzalez D S，Alejo R J P，Cantu-Sifuentes M，et al.A non-linear fuzzy regression for estimating reliability in a degradation process［J］.Applied Soft Computing，2014，16:137-147.

［6］ Alefeld G，Mayer G.Interval analysis:Theory and applications［J］.Journal of Computational and Applied Mathematics，2000，121(1-2):421-464.

［7］ Tanaka H，Lee H.Interval regression analysis by quadratic programming approach［J］.IEEE Transactions on Fuzzy Systems，1998，6(4):473-481.

［8］ 王軍，邱志平，王曉軍.應力強度因子的區間分析方法［J］.航空學報，2008，29(3):611-615.

Wang J，Qiu Z P，Wang X J.Interval analysis for stress intensity factors［J］.Acta Aeronautica et Astronautica Sinica，2008，29(3):611-615(in Chinese).

［9］ Yu I T，Chang C L.Applying Bayesian model averaging for quantile estimation in accelerated life tests［J］.IEEE Transactions on Reliability，2012，61(1):74-83.

［10］ Chateauneuf A.Accelerated life testing and degradation modeling［J］.Reliability Engineering ＆ System Safety，2014，131:228.

［11］ Ye Z S，Xie M.Stochastic modelling and analysis of degradation for highly reliable products［J］.Applied Stochastic Models in Business and Industry，2014，31(1):13-32.

［12］ Park C，Padgett W J.Stochastic degradation models with several accelerating variables［J］.IEEE Transactions on Reliability，2006，55(2):379-390.

［13］ Pan Z Q，Balakrishnan N.Multiple-steps step-stress accelerated degradation modeling based on Wiener and Gamma processes［J］.Communications in Statistics-Simulation and Computation，2010，39(7):1384-1402.

［14］ Li X Y，Jiang T M，Sun F Q，et al.Constant stress ADT for superluminescent diode and parameter sensitivity analysis［J］.Eksploatacja I Niezawodnosc-Maintenance and Reliability，2010(2):21-26.

［15］ Wang X，Jiang P，Guo B，et al.Real-time reliability evaluation with a general Wiener process-based degradation model［J］.Quality and Reliability Engineering International，2014，30(2):205-220.

［16］ Escobar L A，Meeker W Q.A review of accelerated test models［J］.Statistical Science，2006，21(4):552-577.

［17］ Chhikara R S，Folks J L.The inverse Gaussian distribution:Theory，methodology，and applications［M］.New York:CRC Press，1988:23-29.

［18］ Meeker W Q，Escobar L A.Statistical methods for reliability data［M］.New York:John Wiley ＆ Sons，1998:631.