基于像素間孤波的圖像處理模型分析
朱自民,劉榮強 ,劉芬芬,曹有為
(1.哈爾濱工業大學 機電工程學院,哈爾濱150001; 2.東北林業大學 機電工程學院,哈爾濱150040)
從算法來看,數字圖像處理可以分為很多種,傳統的方法如Mallat 小波變換是將圖像分為像素點來處理,現今用的較多的是利用偏微分方程將圖像視為某種場或物理狀態的演化進行處理.圖像在采集、傳輸和存貯的過程中不可避免地會受到外界源的干擾而產生噪聲,要想獲得高質量的圖像信息,濾除噪聲是必不可少的步驟,而濾波效果的好壞會直接影響圖像的處理效果,因此利用算法進行圖像濾波處理至關重要.國外,Osher 和Vese 提出了一個非線性雙曲型的沖擊濾波器模型,利用模型進行邊緣增強和去模糊處理[1];Perona和Malik[2]于1990 年提出圖像去噪模型,為偏微分方程在圖像處理領域的應用開辟了很多新的方向,減弱噪聲的同時模糊圖像區域邊界等特征[3];Shapiro 將離散正交小波變換應用于圖像編碼,得到了比其他圖像編碼方法更好的壓縮效果[4];Mallat 等最早將小波變換應用于信號的奇異性檢驗及圖像多尺度邊緣提取中,取得滿意的實驗結果[5-7].國內學者也對圖像處理的各方面進行了較多的研究,晁銳等改進了小波變換基礎上的圖像融合算法;大連海事大學的郭亮研究了基于偏微分方程的圖像濾波處理,通過實驗證明了改進PM 模型的合理性和有效性;蔡超對基于小波分析和偏微分方程的圖像處理方法進行了細致的研究;董衛軍研究了小波變換在圖像處理中的應用[8-11].
無論哪種算法,在進行圖像處理時,都是將圖像分為連續和離散(數字的)兩種.當圖像函數為連續時,通常采用偏微分方程進行處理;當圖像離散時,多采用隨機理論和小波分析進行處理.本文提出的一種算法[12]是對電荷耦合器件(CCD)傳感器的物理描述,CCD 傳感器在采樣點處數字化,形成像素柵格,這些像素在空間上是分立的,但像素之間的信息結構是相互聯系的,文中利用像素在空間上分立、在信息結構上相聯系的特性,建立了像素之間的時間演化方程.當空間結構信息是非線性時,可得到圖像像素的非線性微分差分方程,分析證明該演化方程具有孤波解的形式,該孤波解在研究中被稱作圖像孤波.首先借助文獻[12]建立時間演化方程,對方程進行分析求解,提出基于孤波的圖像處理模型,并應用于圖像濾波處理.
1 圖像孤波模型的建立
圖1 和圖2 分別建立了一維和二維圖像像素柵格動力系統模型.
圖1 表示的是一維非線性像素柵格動力學方程,設xn(t)表示第n 個像素值為M 的像元受到相鄰像元影響所產生的效應,F(r)=a(1 -e-br)為像素相互之間的影響效果[12],其中:r 為連續變量,a 為圖像的性質參數,b 為圖像集群性質,集群近景則b 值小,反之則b 值大,而其他像素對它的影響可以忽略不計,則像素作用時間演化方程為[13-14]
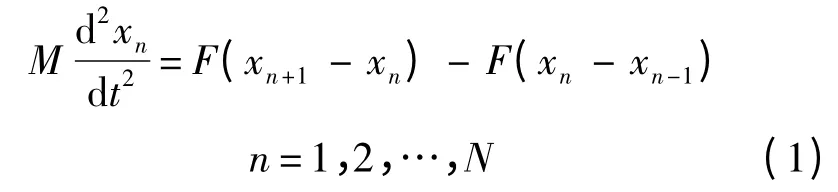
式中:n 為單行像素柵格中像素點的分布,故為整數;N 為行像素的最大值;xn為第n 個像素的影響效應.r 離散為變量rn,令相對作用效果為

結合式(1)則:
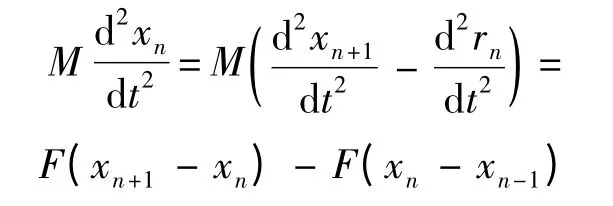
進一步化簡:
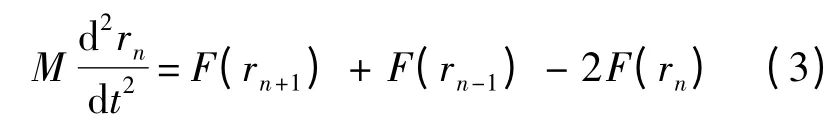
結合公式F(r)=a(1 -e-br)對式(3)進行化簡:
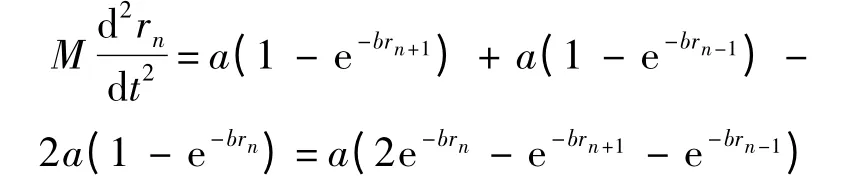
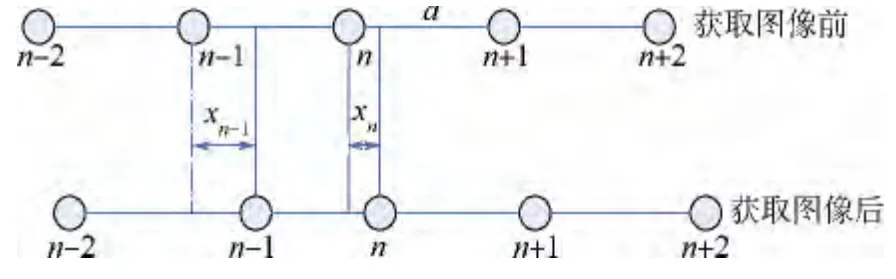
圖1 一維圖像像素柵格動力系統模型Fig.1 One-dimensional image pixel grid power system model
進一步推導,式(3)可化為
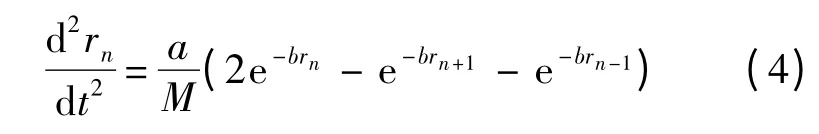
式(4)是標準的非線性微分差分方程,由于式(4)中n 為整數,其表明像素作用的時間演化方程有孤波形式的解析解,即圖像孤波解[15]:
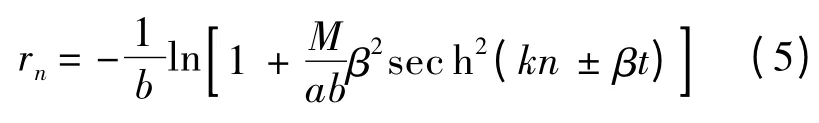
根據圖2 的二維像素柵格方程,考察某像素點受四鄰域像素的影響.利用Hamilton 理論建立四次非線性相互作用下的二維像素影響方程,該方程的Hamilton 為[16]

式中:M、pl,m和ul,m分別為像素的大小、第l 列第m行像素的動量和作用效果;Kx和Ky分別為x 軸方向和y 軸方向的作用效果常數.結合文獻[12]可知,式(6)等價于二維非線性薛定鍔方程[17]:
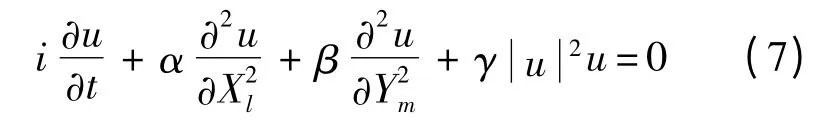
式中:u 為像素間影響效果;Xl為x 軸方向上的影響;Ym為y 軸方向上的影響;γ 和α 為對應的影響系數.
式(7)也具有孤波解,并可簡化方程組:
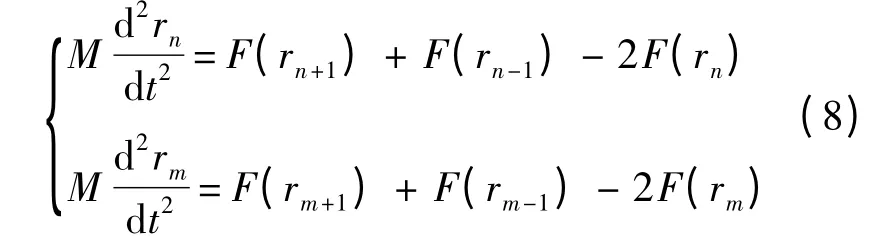

圖2 二維圖像像素柵格Fig.2 Two-dimensional image pixel grid
當m,n 代表x 軸和y 軸時,方程組(8)表示孤波在笛卡兒坐標系中橫向和縱向的傳播.由式(1)可知,二維圖像像素影響方程的解可以根據一維模型的解直接推出,這就是圖像的二維模型.
2 孤波圖像處理模型性能分析
根據像素動力學方程,本節對模型性能進行分析并應用此動力學方程來對圖像進行處理.像素柵格方程實際上是一個非線性微分-差分方程,若按照偏微分方程在圖像處理中的方法,直接利用演化方程對圖像進行處理,將會出現很多問題.考慮到方程是非線性且解不唯一的特性,文中詳細分析了孤波性能并根據模型性能對圖像進行處理.
分析孤波間的相互作用,可知像素柵格方程具有多孤波解.實際應用中主要考察2 孤子解的相互作用,具體分析如下:
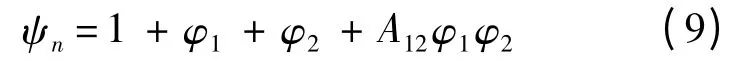
式中:
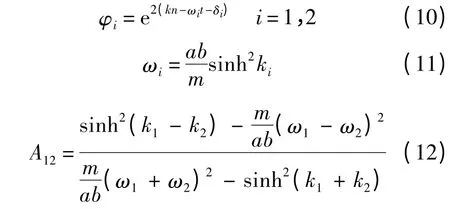
式(10)中φ1和φ2分別對應參數為k1和k2的孤立子解的像素孤波,ω1和ω2的正負性代表像素孤波之間不同的行進方向,文中主要分析像素孤波相對行進的情況,此時ω1和ω2異號.
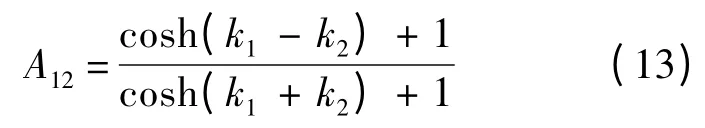

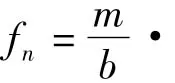
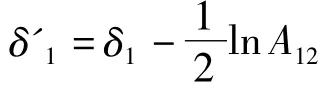
3)當φ1≤1,φ2≤1 時,ψn≈1,(ln ψn)tt≈0,即fn?1;當φ1?1,φ2?1 時,ψn≈A12φ1φ2,(ln ψn)tt=(ln φ1)tt+ (ln φ2)tt≈0,即fn?1;當φ1?1,φ1φ2≈1 時,ψn≈φ2,而φ2?1,φ1φ2≈1時,ψn≈φ1,均有(ln ψn)tt≈0,即fn?1;均表示沒有像素孤波.
4)當φ1≈1,φ2≈1 時,兩個像素孤波非線性疊加.
利用上面像素孤波的存在情況來分析在整個時間軸演化時波形的變化情況進行討論:
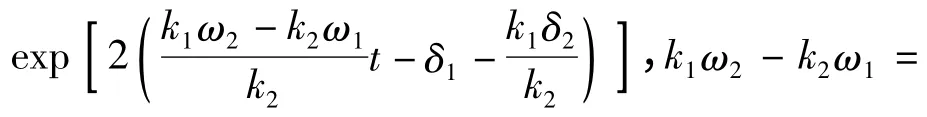
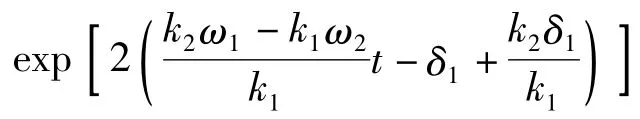
3)除去上述的其他地方,φ1、φ2很小或者是很大,fn≈0,即表示沒有像素孤波.
當|t| 很大時,φ1≈1 與φ2≈1 都不同時成立;所以當t→-∞或t→∞時,k1波與k2波都是彼此分離地獨立運動著,沒有相互作用.但當t 在[-∞,∞]演化時,參數k1的波逐漸追趕上參數k2對應的波,當達到φ1≈1,φ2≈1 的位置時,兩個像素孤波便會發生相互作用,作用后參數k1波將超前于參數k2的波,兩個像素孤波又相互分開各自獨立運動.
兩個像素孤波發生相互作用的具體位置n 和時間t 則由k1n-ω1t-δ1=k2n -ω2t-δ2=0 來求解,結果為


說明模型存在兩個像素孤波,且兩個孤波可以相互影響,影響過后又可恢復到各自的原來狀態,這樣穩定的孤波具有原子性,對其他像素產生影響自身卻并不發生改變,因此可以用孤波代替圖像的像素.
相互作用后的兩個孤波形狀和速度都沒有改變,只是像素孤波的相位發生了改變.因此從相位改變中提取圖像的方位信息,建立一種映射將相位偏移轉化為方位信息Ψ' =Ψ +ψ,其中Ψ 為孤波的前進方向,ψ 為相位的偏移方向,Ψ'為相位改變后的方向.同時,兩個孤波產生碰撞時像素孤波的幅值是非線性疊加的,這個非線性疊加的幅值即像素之間相互影響的大小.
3 模型在圖像濾波中應用
由第2 節的論述可知,像素柵格方程有很多孤波解,但眾多的孤波解并不能直接用于方程演化,文中利用方程的解直接作用到像素上也就是用孤波代替像素.應用文中的模型對圖像進行濾波處理,主要注意如下幾點:
1)孤波模型具有解析解,可以直接代替像素,孤波幅值的變化與參數k1和k2有關且與波的寬度成反比,不同的參數值可以得到不同尺度的孤波,處理中將歸一化的像素值作為孤波初始值,本文利用像素歸一化的灰度值作為初始化的參數,通過乘以相應的系數k 來改變參數得到像素孤波.
2)處理圖像時只需考慮初始相位的孤波解.
3)雖然像素柵格方程是隨時間演化的,但圖像處理時只考慮相對碰撞發生時刻.
4)處理時給出像素孤波碰撞產生相互影響的方向信息.
5)建立4 鄰域孤波模板,將1)~4)放在一個處理模板里.
6)所建立的模板利用幅值的變化范圍和方向判斷某像素點是否是噪聲.若不能判定則改變孤波的參數值,得到不同尺度的孤波重新進行判斷,重復操作直到得到不同尺度下的圖像的細節.
結合MATLAB,利用上述方法對椒鹽噪聲進行圖像處理的仿真,給出了以k 為參數的圖像濾波,結果如圖3 所示,其中圖3(c)的k1值為1,圖3(d)的k2值為0.8.

圖3 基于孤波的圖像濾波算法仿真Fig.3 Algorithm simulation of image filtering based on solitary waves
4 結 論
本文對像素柵格動力學方程的性能進行分析,給出了利用孤波來進行圖像處理的原因和方法,可以得到:
1)像素柵格方程可以提供圖像的幅值和方向信息,圖像的像素可以用像素孤波來代替.
2)文中采用的算法包含圖像的方向信息,在濾波處理時可以更清晰地突出圖像的邊緣.
3)文中算法處理得到的圖像平滑度低于最優算子,但邊緣和細節信息保留較好,高于一般的濾波算法.
4)處理過程中參數設置不當,算法的非線性效應會造成數值計算的溢出,在對溢出進行歸一化時產生的干擾噪聲,有待進一步深入研究.
References)
[1] Vese L,Osher S.The level set method links active contours,mumford-shah segmentation,and total variation restoration,CAMreport 02-05[R].Los Angeles,CA:CAM Report,2002.
[2] Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.
[3] Xiao Z T,Xu Z B,Zhang F,et al.ESPI filtering method based on anisotropic coherence diffusion and Perona-Malik diffusion[J].Chinese Optics Letters,2013,11(10):43-46.
[4] Shapiro J M.Embedded image coding using zero-tree of wavelet coefficients[J].IEEE Transactions on Signal Processing,1993,41(12):3445-3462.
[5] Mallat S,Zhong S F.Characterization of signals from multiscale edges[J].IEEE Transactions on PAMI,1992,14(7):710-732.
[6] Mallat S.Multiresolution representation and wavelets[D].Philade,PA:University of Pennsylvania,1988.
[7] Rafiullah C,Asifullah K,Adnan I.Wavelet based image authentication and recovery[J].Journal of Computer Science & Technology,2007(6):795-804.
[8] 晁銳,張科,李言俊.一種基于小波變換的圖像融合算法[J].電子學報,2004,32(5):750-753.
Chao R,Zhang K,Li Y J.An image fusion algorithm using wavelet transform[J].Acta Electronica Sinica,2004,32(5):750-753(in Chinese).
[9] 郭亮.基于偏微分方程的圖像濾波方法研究[D].沈陽:大連海事大學,2013.
Guo L.PDE-based research on image filtering methods[D].Shenyang:Dalian Maritime University,2013(in Chinese).
[10] 蔡超.基于小波和偏微分方程的圖像處理方法與應用[D].武漢:華中科技大學,2005.
Cai C.Wavelet and partial differential equation based image processing methods and their applications[D].Wuhan:Huazhong University of Science and Technology,2005(in Chinese).
[11] 董衛軍.基于小波變換的圖像處理技術研究[D].西安:西北大學,2006.
Dong W J.Image processing technique research based on wavelet transform[D].Xi’an:Northwest University,2006(in Chinese).
[12] Zhu Z M,Liu R Q,Cao Y W,et al.Image processing algorithm based on solitary wave[J].Applied Mechanics and Materials,2014(539):126-130.
[13] 田強.晶格振動簡正坐標的具體表述及其討論[J].大學物理,1999(8):7-8.
Tian Q.Discussions on some relations about ortho-coordinate[J].College Physics,1999(8):7-8(in Chinese).
[14] 陳登遠.孤子引論[M].北京:科學出版社,2006:39-41.
Chen D Y.An introduction to soliton[M].Beijing:Science Press,2006:39-41(in Chinese).
[15] Hirota R.Exact solutions of Kortewerg-de veris equation for multiple collisions of solutions[J].Physical Review Letters,1971,27(18):1192-1194.
[16] Remoissenet M.Waves called solitons[M].2nd ed.Berlin Heidelberg:Springer,1999:138-204.
[17] Sulem C,Sulem P L.The nonlinear Schrodinger equation:Selffocusing and wave collapse[M].New York:Springer New York Inc.,1999:57-92.

