雙電磁航天器編隊構型保持自適應控制

徐增文，師鵬，趙育善

(北京航空航天大學 宇航學院，北京100191)

衛星編隊飛行技術在合成孔徑雷達、空間干涉儀以及在軌組裝等方面具有明顯優勢.考慮到發射成本和能量消耗，目前編隊飛行任務大多采用被動形式的編隊控制方式，即相對運動過程中較少使用推力器對編隊構型進行控制.隨著空間任務朝著多樣化和復雜化的方向發展，對衛星編隊飛行的相對軌道控制能力提出了更高的要求，主動形式的衛星編隊控制方式逐漸受到重視.但采用基于沖量原理的火箭發動機進行編隊構型控制存在以下幾個方面的缺點:①火箭發動機噴射出的羽流會影響臨近衛星上的觀測器件;②所攜帶的推進劑，既增加了衛星發射成本，也成為限制衛星在軌壽命的主要因素.

采用星間電磁力［1-2］、靜電力［3］和洛倫茲力［4］等非接觸力的無工質推進方式逐漸得到關注.利用航天器之間的電磁力進行相對軌道控制的編隊稱為電磁航天器編隊.由于控制力的產生基于電磁場之間的相互作用，不需要消耗燃料，所以電磁航天器編隊飛行能夠很好地克服上述問題.

美國麻省理工學院和馬里蘭大學對電磁航天器編隊飛行的可行性、地面試驗和在軌驗證等進行了長期深入的研究.Miller 等［1-2，5］首次提出電磁編隊飛行的概念，并研究了在TPF 計劃中采用電磁編隊飛行技術的可行性.Hashimoto 等［6］提出采用超導線圈進行電磁編隊.Elias 等［7］針對兩顆電磁航天器相對運動提出了一種非線性動力學模型.Ahsun 和Miller 等［8-9］提出了n 顆電磁航天器編隊的非線性自適應控制律.2013 年8 月3 日，美國馬里蘭大學的RINGS 項目中的兩顆電磁航天器搭載HTV-4飛船進入國際空間站進行在軌試驗，分別對電磁編隊飛行技術和星間電能無線傳輸技術進行驗證，這是電磁航天器編隊飛行技術第一次在軌飛行試驗［10］.

近年來國內學者也對電磁航天器編隊飛行進行了相關研究［11-13］.張元文等［14］采用反饋線性化及魯棒H∞方法，研究了空間電磁對接的魯棒協調控制問題.北京航空航天大學的蘇建敏和董云峰［15］基于人工勢函數法研究了多顆電磁航天器的編隊控制問題;張皓［16］和邵龍飛［17］的研究表明，多顆電磁航天器的編隊構型控制問題可以通過序列控制轉化為多階段的兩顆電磁航天器相對運動控制.

本文重點研究了兩顆電磁航天器的編隊構型保持問題，所采用的自適應控制方法可以推廣到多顆電磁航天器編隊構型控制問題.首先，介紹了電磁航天器編隊飛行的基本原理.然后，根據星間電磁控制力計算公式反推控制電流時，考慮兩電磁航天器能量消耗的均衡性要求，得到了兩星能量消耗均衡的解析解.針對電磁航天器編隊構型保持問題，采用基于極坐標的電磁航天器相對運動動力學模型，并考慮工程實際中存在的未知干擾力和電磁模型的參數不確定性，設計了編隊構型保持自適應控制律.最后，通過數值仿真驗證了控制方法的有效性.

1 電磁航天器編隊飛行原理

電磁航天器編隊飛行是一種新的不消耗燃料的衛星編隊形式.編隊中各成員衛星稱為電磁航天器，其上安裝有3 個正交的超導線圈.圖1 為電磁航天器的概念設計圖.當線圈充電時，航天器周圍會產生磁場，根據畢奧-薩伐爾定律，可以計算得到航天器周圍的磁場分布情況，然后再根據安培定律可以求得磁場中另一航天器所受到的電磁力及電磁力矩.本文研究的電磁航天器編隊飛行采用軌道優先的解耦控制策略，即采用星間電磁力控制相對軌道運動，由于電磁力矩所引起的姿態控制問題在這里不做贅述.

圖1 電磁航天器概念設計Fig.1 Conceptual design of electromagnetic spacecraft

為描述電磁航天器相對于編隊質心的運動，首先定義旋轉軌道坐標系O，假設其原點位于編隊系統質心，x 軸指向軌道矢徑方向，y 軸指向軌道面法線方向，z 方向由右手法則確定.假設兩顆電磁航天器組成的編隊系統為剛體，定義與剛體固連的本體坐標系為B，坐標系原點位于系統質心，x 軸由航天器1 指向航天器2.軌道坐標系O繞z 軸旋轉歐拉角ψ，然后繞新的y 軸旋轉歐拉角－θ，即可得到本體系B.

在計算星間電磁力過程中，為避免復雜的二次曲面積分運算，目前的研究中大多采用遠場近似模型，當星間距離r 大于線圈半徑R 的8 倍時，編隊中的兩顆電磁航天器可以假設為遠場中的兩個磁偶極子，如圖2 所示.

每個磁偶極子的磁矩可以記為μ，其幅值為

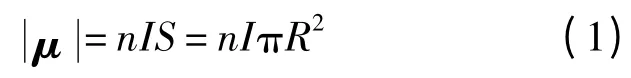
式中:n 為通電線圈匝數;I 為線圈中的電流大小;S 為圓形線圈面積.磁偶極子的方向可由安培右手定則確定.

根據電磁場計算原理，可以得到兩電磁航天器之間電磁力的計算公式［8-9］:

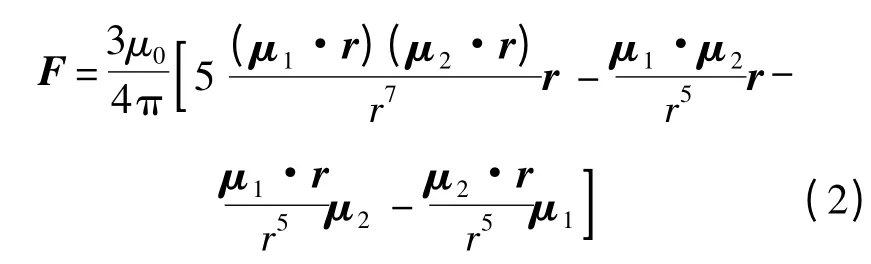
式中:μ0為真空磁導率;r 為航天器1 到航天器2的位置矢量;μ1和μ2為兩航天器線圈的磁矩.

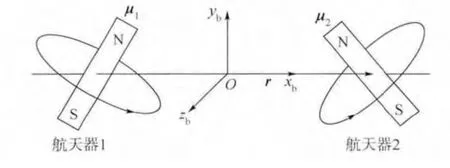
圖2 遠場近似模型示意圖Fig.2 Diagram of far-field approximate model

式(2)給出了星間電磁力的表達式，已知電磁線圈中電流的大小和相對位置矢量時，可以計算出電磁航天器相互之間的電磁力.實際上，為了對電磁航天器進行控制，需要求解相應的逆問題，即在已知電磁控制力的情況下，計算出各電磁航天器的磁矩，進而求解出相應的控制電流.一種方法是，假設其中一個磁偶極子的磁矩是確定的，然后通過求解一個非線性方程組，得到另一個磁偶極子的磁矩.但這種情況下無法保證編隊中各航天器的能量消耗是均衡的，當某一電磁航天器上的能量消耗殆盡時，就意味著整個航天器編隊任務的結束，所以電磁航天器編隊飛行需要考慮成員航天器能量消耗的均衡性.

對于兩顆電磁航天器編隊飛行的情況，能量消耗均衡最理想的情況是兩個磁偶極子所消耗的能量完全相同，即μ1=μ2.

假設μ1=μ2，對式(2)進行求解，可以得到系統本體坐標系B 下磁偶極子磁矩的解析解:

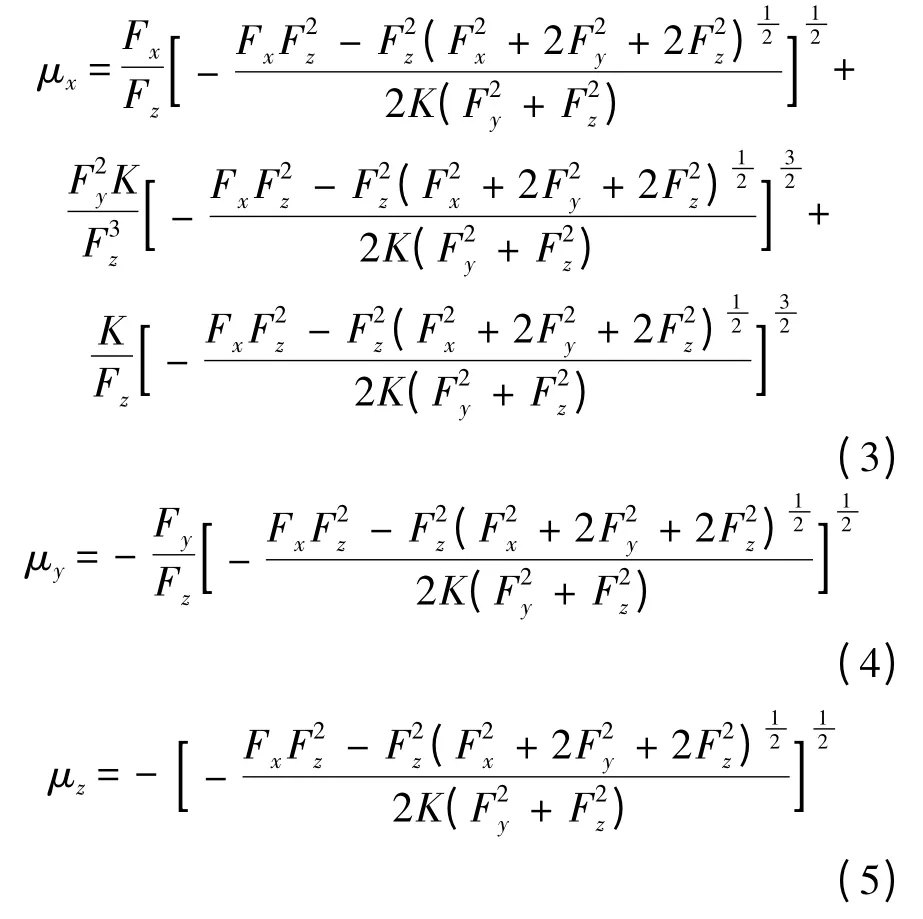
式中:K=3μ0/(8πr4).

對于兩顆電磁航天器的編隊飛行，采用式(3)～式(5)對航天器的磁矩進行分配，可以使兩航天器消耗的能量完全相同，從而保證編隊中成員航天器能量消耗的均衡性，延長航天器編隊的運行壽命，這點也是傳統推進方式所不具備的優勢.

2 電磁編隊相對軌道動力學模型

本節借鑒繩系衛星系統的動力學方程推導過程，建立兩顆電磁航天器編隊飛行的非線性相對運動動力學模型.同時，該動力學模型也可以用來描述其他類型的非接觸力航天器編隊的相對運動.

軌道坐標系O 中的兩電磁航天器的位置矢量可以表示為［3］

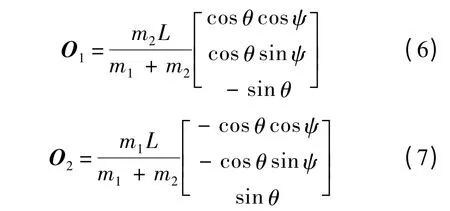
式中:L 為兩航天器之間的距離;m1和m2為兩航天器的質量.

系統的動能可以表示為

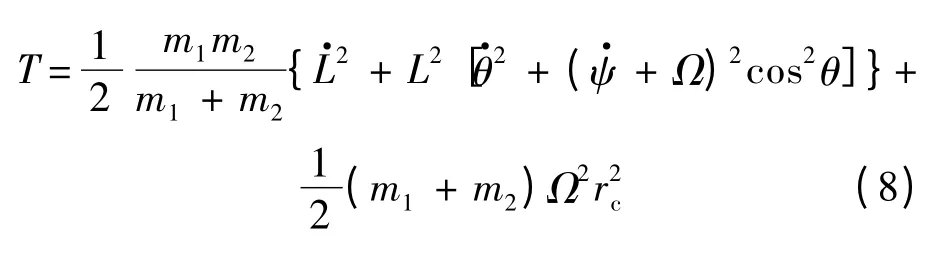
編隊系統重力勢能的二階非線性表達式可記為

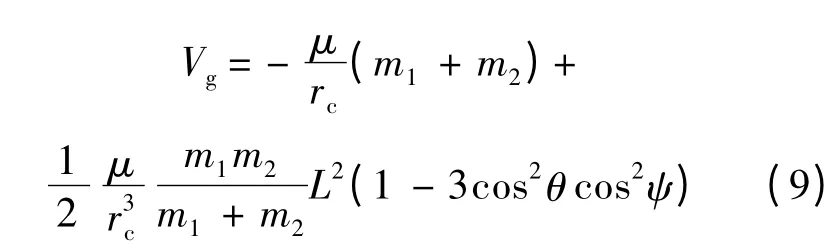
相應的，編隊系統的電磁勢能記為Vm.

兩電磁航天器編隊系統的拉格朗日方程可以寫成如下形式［18]

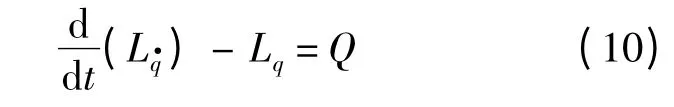
式中:Q 為廣義坐標q 下的廣義力.

將式(8)、式(9)代入式(10)中并寫成分量形式，假設電磁航天器編隊系統質心所在軌道為圓軌道，可以得到關于相對距離L、軌道面內旋轉角ψ 和滾轉角θ 的電磁航天器相對運動非線性動力學方程:

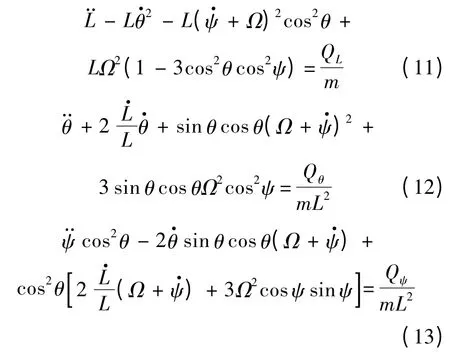
式中:m=m1m2/(m1+m2);QL、Qψ和Qθ為廣義力，可以分別表示為QL= FL、Qψ= FψL 和Qθ=FθL，其中FL、Fψ和Fθ為3 個方向上的電磁力.電磁航天器編隊飛行過程中，3 個方向上的控制力可由航天器之間的電磁作用產生.

式(11)～式(13)進一步可以記為

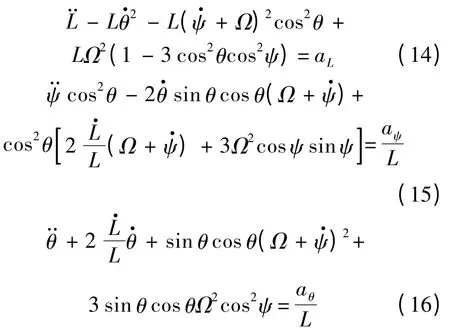
式中:aL、aψ和aθ分別為L、ψ 和θ 3 個方向上的控制加速度.

式(14)～式(16)可以簡記為

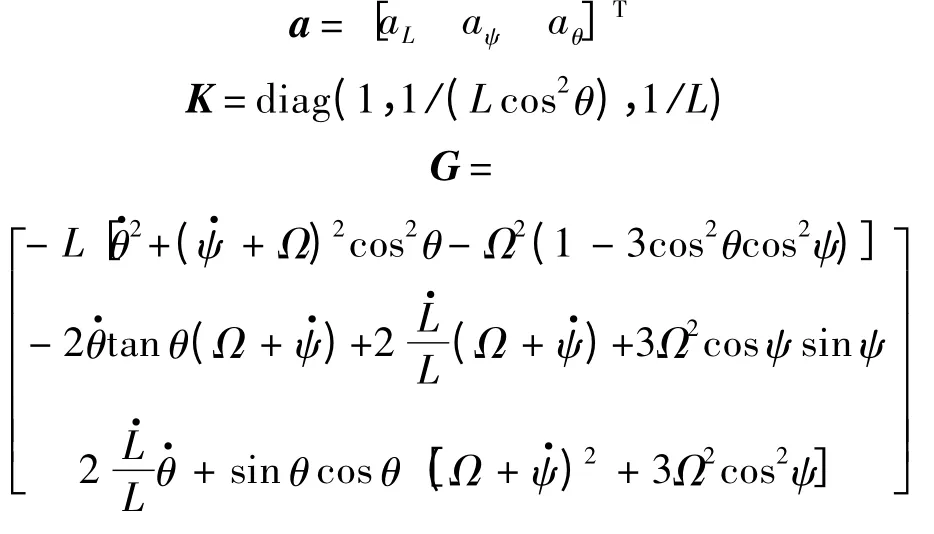
實際上，電磁航天器編隊飛行過程中除了受到相互之間的電磁作用力，還會受到未知的相對干擾力，所以式(17)可進一步表示為

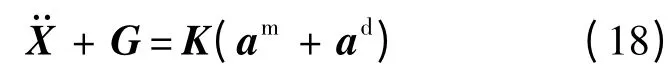
另外，如第1 節所述，電磁航天器之間電磁力的計算模型是基于遠場近似得到的，所以其與真實值存在一定的誤差，電磁力的真實值可以通過對遠場近似模型的計算值進行修正得到.本文用式(19)表示電磁航天器控制加速度的真實值［8-9］:

因此，考慮未知干擾力和電磁作用遠場近似模型的不確定性，兩顆電磁航天器編隊飛行的相對運動動力學方程可以記為

式中:

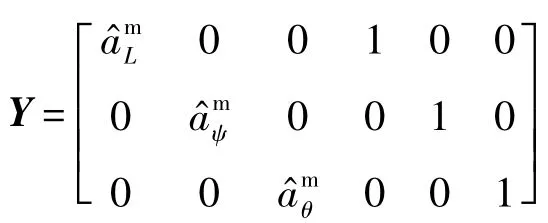
3 編隊構型保持自適應控制

本節將在相對運動動力學模型的基礎上，針對電磁航天器編隊構型保持設計自適應控制律.假設電磁航天器編隊構型的期望狀態為Xd(t)，期望速度為為不確定參數的估計值.狀態誤差可以表示為

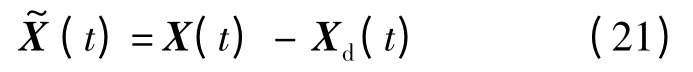
速度誤差為

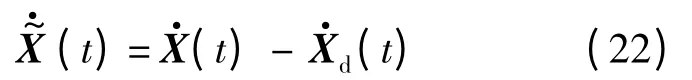
不確定參數的估計誤差為

復合誤差可以記為

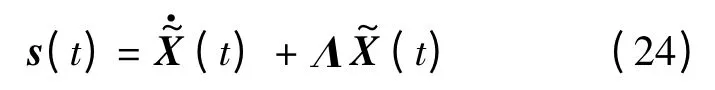
對式(24)求導可得

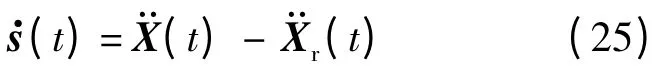
為設計電磁航天器編隊構型保持自適應控制律，取李雅普諾夫函數［19］為

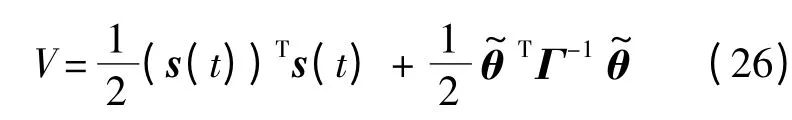
式中:Γ 為大于零的對角矩陣.

對式(26)求導得

為實現編隊系統的李雅普諾夫穩定性，取如下控制律:

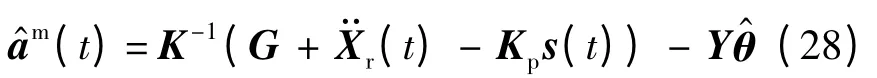
同時，取自適應律為

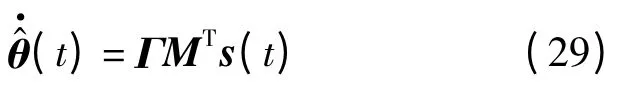
式中:M=KY.

則式(27)可以化為

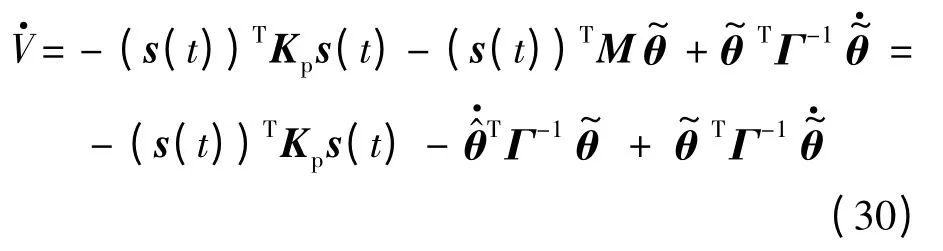
假設外界未知干擾力和電磁模型不確定性修正因子都是隨時間慢變的，則式(30)可以化為

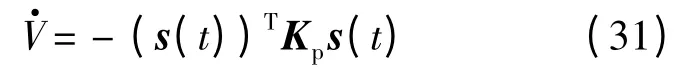
4 數值仿真

本節通過數值仿真算例對電磁航天器構型保持自適應控制律進行驗證.

電磁航天器編隊構型保持仿真參數如下:編隊系統質心所在參考軌道為圓軌道，其半長軸為a=7 000 km;假設編隊中兩電磁航天器的質量相同，即m1=m2=100 kg;其上的電磁作用機構由3個正交的圓形超導線圈構成，線圈半徑R =1 m，線圈匝數n=100.

根據空間任務的需要，希望電磁航天器編隊系統能夠沿地球矢徑方向保持懸停構型，期望構型的具體參數如下:

假設初始時刻電磁航天器編隊構型相對于期望構型有一定的誤差:

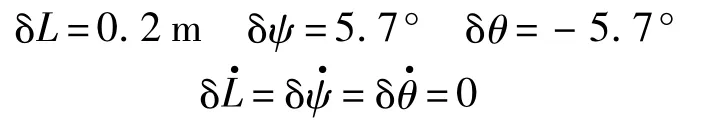
考慮電磁航天器編隊飛行過程中受到的未知干擾力和電磁作用遠場近似模型的不確定性修正因子，對不確定性參數進行如下假設:

1)由于編隊中兩顆電磁航天器之間的距離遠遠大于超導線圈的半徑，采用遠場模型即可滿足精度要求，可以認為由模型計算得到的電磁力是準確的，所以將電磁作用遠場近似模型的不確定性修正因子假設為［γix;γiy;γiz］=［0;0;0］.

自適應控制的相關參數設置如下:

Λ=diag(0.001，0.001，0.001)

Kp=diag(0.05，0.05，0.05)

Γ=diag(1，1，1，0.1，0.1，0.1)

圖3 給出了徑向誤差δL 隨時間的變化情況，圖4 給出了面內旋轉角誤差δψ 和滾轉角誤差δθ隨時間的變化情況，約1.5 個參考軌道周期后，徑向誤差收斂到1 ×10－4m，角度誤差都收斂到8 ×10－6rad.仿真結果表明，在自適應控制律的作用下，編隊構型達到了期望值，說明所設計的編隊構型保持控制律是有效的.

圖5 顯示的是電磁航天器編隊構型保持過程中L、ψ 和θ 3 個方向上的控制加速度.從圖中可以看出，L 方向上的控制加速度的量級在10－5m/s2，而ψ 和θ方向上的控制加速度非常小.

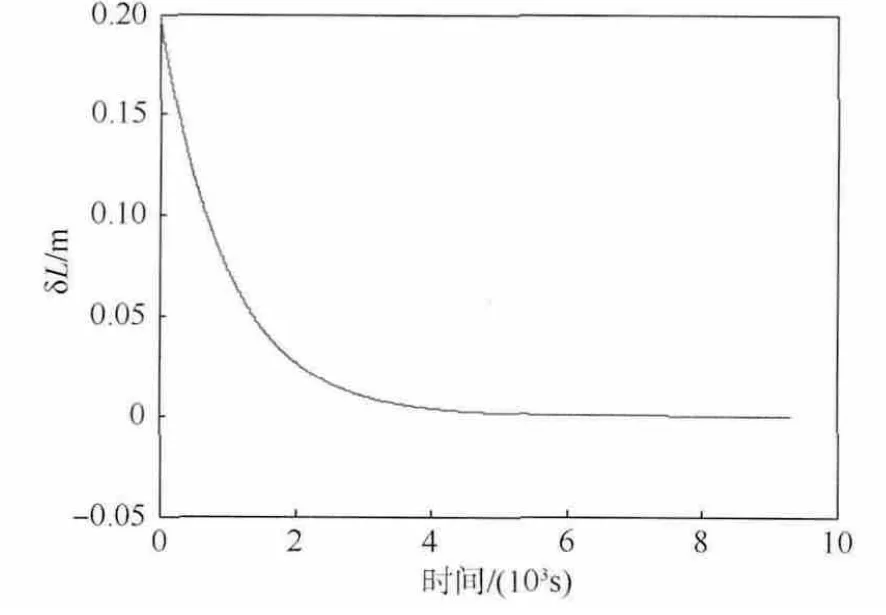
圖3 誤差δL 隨時間變化曲線Fig.3 Histories of error δL changing with time

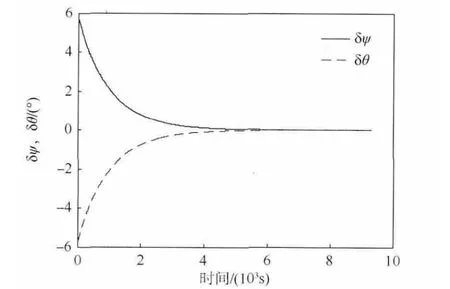
圖4 誤差δψ 和δθ 隨時間變化曲線Fig.4 Histories of error δψ and error δθ changing with time

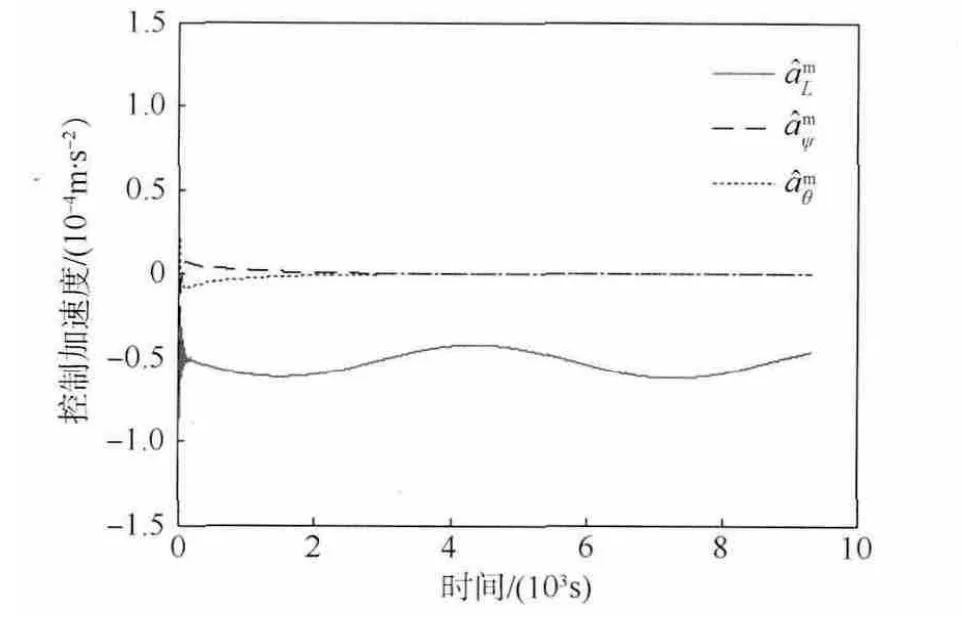
圖5 控制加速度隨時間變化曲線Fig.5 Histories of control accelerations changing with time

圖6 和圖7 分別給出了干擾加速度和電磁模型不確定性修正因子的估計值.從圖6 中可以看出，L 方向上的干擾加速度估計值呈現出正弦變化的趨勢，其大小和變化趨勢都與所假設的未知干擾加速度非常一致;而另外兩個方向上的干擾加速度估計值幾乎為零，這也與之前的假設是吻合的.從圖7 中可以看出，遠場近似模型不確定性修正因子估計值的量級為10－8的，幾乎可以忽略不計，這與仿真中所假設的不確定性修正因子是一致的.

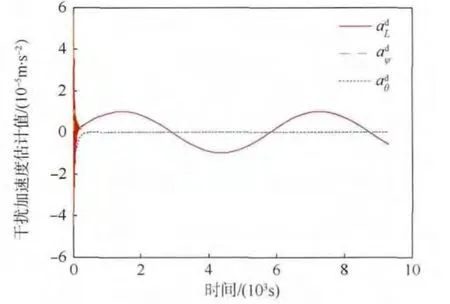
圖6 干擾加速度隨時間變化曲線Fig.6 Histories of disturbed accelerations changing with time

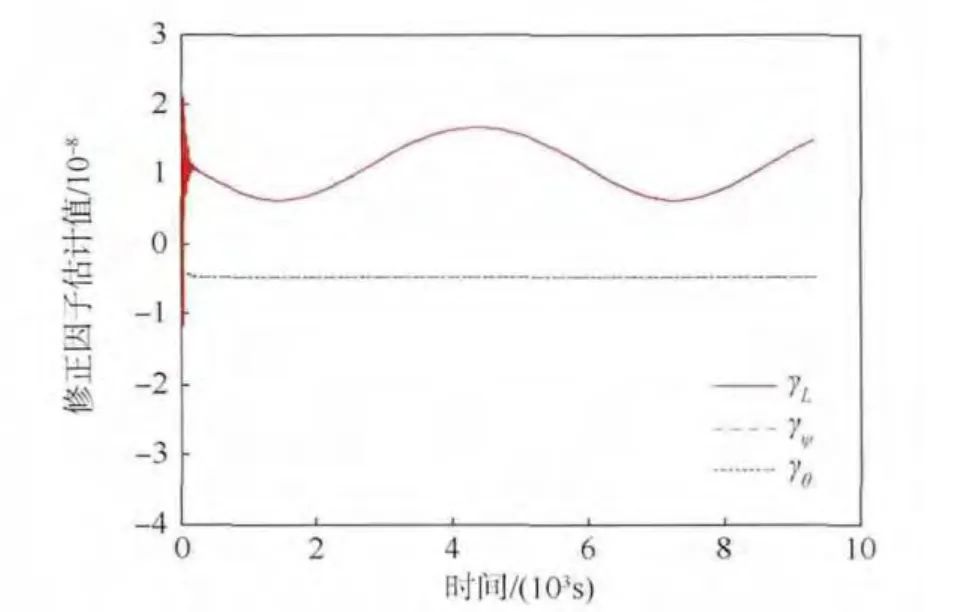
圖7 不確定性修正因子隨時間變化曲線Fig.7 Histories of adjustment factors changing with time

結合圖5 和圖6 的仿真結果，可以發現外界干擾加速度對編隊構型保持造成了影響，控制加速度隨時間變化曲線中所表現出的三角函數變化趨勢說明了這點.

仿真結果表明，不確定性參數快速收斂到真實值，說明本文所設計的電磁航天器編隊構型保持自適應控制律對未知干擾加速度和電磁作用遠場近似模型不確定性修正因子進行了準確估計.

圖8 顯示的是電磁航天器上3 個正交超導線圈中控制電流隨時間的變化曲線.從圖中可以看出線圈中的控制電流最大值小于100 A，可以采用超導線圈實現.需要指出的是，圖中所給出的控制電流結果是采用式(3)～式(5)計算得出的，編隊中兩電磁航天器上超導線圈中的控制電流的大小是相同的，在編隊構型保持過程中其各自所消耗的電能也是完全相同的，這就保證了編隊系統中各航天器能量消耗的均衡性，更有利于實現長期的編隊構型保持.

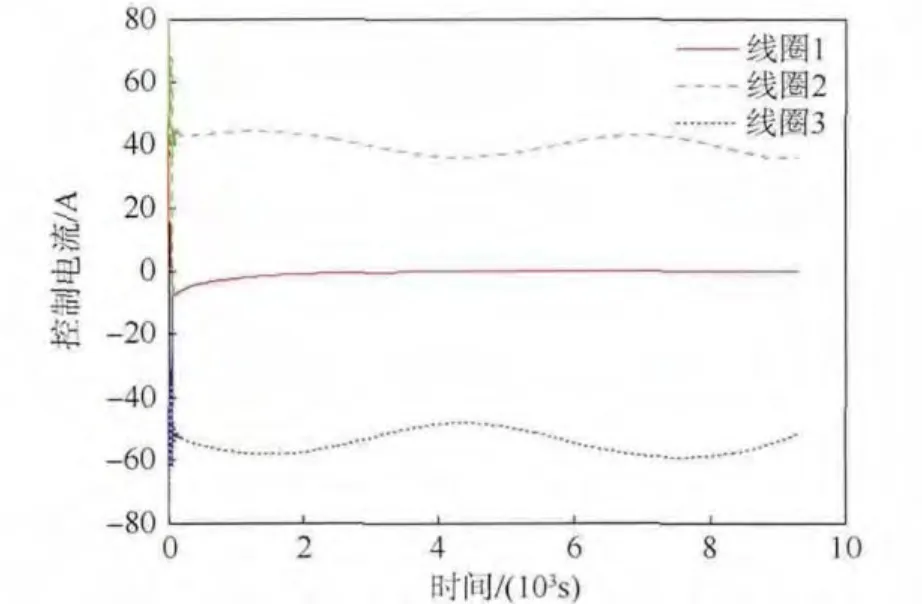
圖8 線圈中電流隨時間變化曲線Fig.8 Histories of currents in coils changing with time

5 結 論

相對于傳統的消耗燃料的推進方式，利用星間電磁力進行編隊構型保持的電磁航天器編隊飛行在未來的空間任務中具有重要的應用價值.本文對電磁航天器編隊構型保持控制進行了研究，得到以下結論:

1)所提出的求解兩電磁航天器控制磁矩的解析表達式，是一種新的磁矩分配方式，對研究編隊飛行過程中各成員航天器能量消耗的均衡性提供了一條新的解決思路.

2)針對電磁航天器編隊構型保持實際可能面臨的未知干擾力和電磁作用遠場近似模型的不確定性，可以采用自適應控制方法.通過設計自適應控制律，編隊構型能夠從初始狀態收斂到期望值，表現出良好的控制性能，同時未知干擾力和電磁模型不確定性修正因子的估計值也很快收斂到真實值.

此外，本文研究的電磁航天器編隊構型保持自適應控制方法可以為多顆電磁航天器編隊的構型保持和重構奠定技術基礎.

References)

［1］ Miller D W，Sedwick R J.Electromagnetic formation flight phase I report［R］.Massachusetts:Massachusetts Institute of Technology，2003.

［2］ Sedwick R J，Miller D W.Electromagnetic formation flight final report［R］.Massachusetts:Massachusetts Institute of Technology，2005.

［3］ Inampudi R，Schaub H.Optimal reconfigurations of two-craft coulomb formation in circular orbits［J］.Journal of Guidance，Control and Dynamics，2012，35(6):1805-1815.

［4］ Pollock G E，Gangestad J W，Longuski J W.Inclination change in low earth orbit via the geomagnetic Lorentz force［J］.Journal of Guidance，Control and Dynamics，2010，33(5):1387-1395.

［5］ Kong E M C，Kwon D W，Schweighar S A，et al.Electromagnetic formation flight for multisatellite arrays［J］.Journal of Guidance，Control and Dynamics，2004，41(4):659-666.

［6］ Hashimoto T.Formation flight control using super conducting magnets［D］.Massachusetts:Massachusetts Institute of Technology，2002.

［7］ Elias L M，Kwon D W，Sedwick R J，et al.Electromagnetic formation flight dynamics including reaction wheel gyroscopic stiffening effects［J］.Journal of Guidance，Control and Dynamics，2007，30(2):499-511.

［8］ Ahsun U.Dynamics and control of electromagnetic satellite formations［D］.Massachusetts:Massachusetts Institute of Technology，2007.

［9］ Ahsun U，Miller D W，Ramirez J L.Control of electromagnetic satellite formations in near-earth orbits［J］.Journal of Guidance，Control and Dynamics，2010，33(6):1883-1891.

［10］ Alinger D J.System analysis and design for the resonant inductive near-field generation system(RINGS)［D］.Maryland:University of Maryland College Park，2013.

［11］ Zeng G Q，Hu M.Finite-time control for electromagnetic satellite formations［J］.Acta Astronautica，2012，74(3):120-130.

［12］ 胡敏，曾國強.分離模塊集群航天器發展概況［J］.裝備指揮技術學院學報，2011，22(4):61-66.

Hu M，Zeng G Q.Developments of the fractionated spacecraft［J］.Journal of the Academy of Equipment Command ＆ Technology，2011，22(4):61-66(in Chinese).

［13］ Xu Z W，Shi P，Zhao Y S.Optimal control of two-craft electromagnetic formation in circular orbit［C］∥Advanced in the Astronautical Sciences Series:24th AAS/AIAA Space Flight Mechanics Meeting.San Diego，CA:Univelt Inc.，2014，152:2547-2561.

［14］ 張元文，楊樂平，朱彥偉，等.空間電磁對接的魯棒協調控制［J］.國防科技大學學報，2011，33(3):33-37.

Zhang Y W，Yang L P，Zhu Y W，et al.Coordinated robust control of space electromagnetic docking［J］.Journal of National University of Defense Technology，2011，33(3):33-37(in Chinese).

［15］ 蘇建敏，董云峰.利用人工勢函數法的衛星電磁編隊控制［J］.北京航空航天大學學報，2012，38(2):213-217.

Su J M，Dong Y F.Artificial potential function method for satellite electromagnetic formation control［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(2):213-217(in Chinese).

［16］ 張皓.庫侖航天器的動力學與控制研究［D］.北京:北京航空航天大學，2012.

Zhang H.The dynamics and control of coulomb spacecrafts［D］.Beijing:Beihang University，2012(in Chinese).

［17］ 邵龍飛.電磁航天器在軌協同運動控制研究［D］.北京:北京航空航天大學，2014.

Shao L F.On-orbit operation cooperative control of electromagnetic spacecraft［D］.Beijing:Beihang University，2014(in Chinese).

［18］ 趙育善，師鵬.航天器飛行動力學建模理論與方法［M］.北京:北京航空航天大學出版社，2012:68-69.

Zhao Y S，Shi P.Spacecraft flight dynamics modelling theory and method［M］.Beijing:Beihang University Press，2012:68-69(in Chinese).

［19］ de Queiroz M S，Kapila V，Yan Q G.Adaptive nonlinear control of multiple spacecraft formation flying［J］.Journal of Guidance，Control and Dynamics，2000，23(3):385-390.