改進LeaderRank算法的意見領袖挖掘

徐郡明，朱福喜，劉世超，朱碧穎

武漢大學 計算機學院，武漢 430072

1 引言

在復雜網絡社區中，各用戶因其環境、性格不同，所起到的作用也有所不同。其中，部分用戶會積極的接受并傳播某些信息和觀點，并且對其他用戶有著重要的影響力，這些用戶即為“意見領袖”。“意見領袖”傳播的信息會影響網絡中另一部分用戶，引導這部分用戶的行為。因此，若使用某些信息影響“意見領袖”，就可能高效地影響到網絡中的大多數用戶。所以，進行“意見領袖”的挖掘，對于利用已成型、穩定的社區網絡進行信息推廣、輿情監測等具有重要的理論及現實意義。

LeaderRank算法是一個有效的意見領袖挖掘算法，本文在該算法的基礎上，結合用戶之間的情感傾向信息和用戶活躍度因素，以提高意見領袖挖掘的準確度。

2 相關研究

新興媒體（如微博、微信等）逐漸滲透到人們的日常生活中，在用戶之間形成了一個“用戶-用戶”的復雜網絡。越來越多的研究人員開始關注信息如何在這個復雜網絡中進行傳播[1]以及如何控制傳播速度[2-4]，從而找到合適的方式促進正確的社會價值信息的傳播，抑制謠言的流行，提高廣告投放的精確度。

Aral等[5]的研究證明意見領袖在復雜網絡的信息傳播中起著關鍵性作用。Bai等[6-7]認為可以將復雜網絡中度最大的節點看作“意見領袖”，通過影響這些節點來控制信息在網絡中傳播，這一方法被應用于多種復雜網絡的意見領袖挖掘[8-10]。

Kitsak等[11]人指出，網絡中節點的傳播能力與節點所處的位置有重要關系，處于網絡核心位置的節點，即使度較小，也會有較高的影響力；反之亦然。與此同時，意見領袖挖掘方面的其他研究人員也陸續提出了大量其他指標，例如接近中心性[12]、特征向量中心性[13]、路由中心性[14]和環中心性[15]。這些指標主要是用來衡量一個節點在網絡中的傳播能力。

Song等[16]借鑒PageRank算法對用戶進行排名，并結合用戶之間情感傾向分析、評論隱含關系分析、評論的時間衰減等因素挖掘復雜網絡中的意見領袖。但使用PageRank算法不適合在結構快速變化的復雜網絡中挖掘意見領袖。

鑒于PageRank算法在意見領袖挖掘方面表現出來的種種問題，Lv等人[17]提出了一種意見領袖挖掘的新算法——LeaderRank算法。在意見領袖挖掘方面，Leader-Rank算法比PageRank算法的準確性更高，面對噪音和惡意攻擊時的穩定性更強。

Li等[18]針對LeaderRank算法進行改進，提出加權的LeaderRank算法，并通過實驗驗證了加權的LeaderRank算法具有更好的準確性和穩定性。

因此，國內外學者在意見領袖挖掘研究工作中非常注重LeaderRank算法。但LeaderRank算法及其加權改進算法也存在一些可改進之處，例如：算法沒有考慮網絡中“用戶之間的情感傾向”、“用戶活躍程度”等因素對意見領袖挖掘的影響，這會制約算法性能的進一步提升。本文旨在這些方面做出改進。

3 意見領袖發現算法

3.1 PageRank算法分析

PageRank算法將對頁面的鏈接看成投票，實現將互聯網中“鏈接價值”概念作為排名因素。PageRank算法將計算得到的網頁在不同時刻的得分作為衡量網頁重要性的標準。PageRank算法的核心公式如式（1）所示：

其中，N表示頁面總數；Pi(t)表示在t時刻，i頁面的得分；αji表示當頁面j中是否存在指向頁面i的超鏈接，存在時，αji=1，否則，αji=0；表示j頁面中指向其他頁面的超鏈接的個數；當=0時，=1 ，當≠0時，=0；c是“跳轉概率”，當一個用戶訪問一個頁面時，以概率c通過地址欄，隨機跳到其他網頁，以概率1-c通過網頁中的超鏈接跳轉到其他網頁。

在網絡結構快速變化的社會網絡中，PageRank算法的“跳轉概率”c的最佳值，需要隨著網絡結構的變化而不斷調整。針對某一特定結構的網絡，要經過多次訓練才能得到參數c的最佳取值，這對于結構變化頻繁的網絡并不適用。除此之外，社交網絡是一個非連通圖，而PageRank算法并不保證在非連通圖上具有收斂性。上述兩原因導致PageRank算法在意見領袖挖掘方面有很大限制。

3.2 LeaderRank算法分析

Lv等[17]提出的LeaderRank算法，對PageRank算法的改進主要是在網絡中添加一個公共節點“Ground Node”，并讓此節點連接網絡中的全部節點，這樣一個N節點M邊的網絡G(N，M)就變成N+1節點M+2N邊的網絡G(N+1，M+2N)。

添加“Ground Node”的作用如下：

（1）由于“Ground Node”連接了網絡中其余各節點，從而形成一個連通圖，這就保證了LeaderRank算法的收斂性。不僅如此，“Ground Node”的加入還減小了整個網絡的半徑，增加收斂速度。

（2）某i節點的信息來源（即由i節點發出的指向其他節點的邊）的多少反比于節點i流向“Ground Node”節點的個數。隨著網絡結構的變化，不同的節點會有不同的“跳轉概率”。LeaderRank算法不再需要參數“跳轉概率”c。

Lü等[17]還通過實驗證明了LeaderRank算法具有更高的準確性和更強的穩定性。LeaderRank算法的核心公式如式（2）、（3）所示：

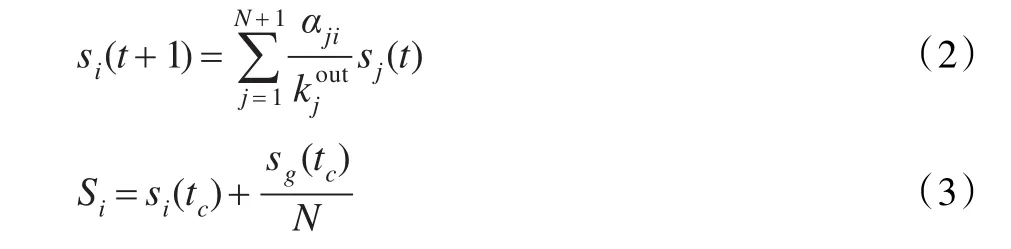
其中，si(t)表示i節點在t時刻的得分；tc表示si(t)收斂的時刻；sg(tc)表示在tc時刻“Ground Node”節點的得分；Si表示i節點最終的得分，其他變量含義同式（1）。

3.3 LeaderRank算法的缺陷分析

在現實網絡中，用戶之間存在明顯的觀點差異或是有相當數量的惡意注冊用戶，都會導致意見領袖排名出現偏差，而LeaderRank算法會受到這兩方面因素的影響。因此，改進的LeaderRank算法增加了用戶的情感傾向和惡意注冊用戶兩個方面考察。

3.3.1 用戶的情感傾向

用戶可以接受其他信息源的某個觀點并加以傳播，也可以反對其他信息源的觀點并阻礙其傳播。這取決于用戶的情感傾向。例如在微博中，粉絲中有所謂的“紅粉”（支持博主觀點）和“黑粉”（反對博主觀點）之分，如圖1所示，第一、三條是支持博主的評論，而第二條反對博主的評論。而之前的LeaderRank算法都沒有考慮到用戶之間的情感傾向。

圖1 某微博評論圖

在微博中，存在一些特殊符號，例如@、#等，在圖1中的第三條微博回復中，此用戶（用戶A）就使用了@符號，指向其他用戶（用戶B、用戶C）。雖然用戶A不是直接被用戶B、C的微博內容影響，但用戶B、C的其他行為顯然也影響到了用戶A（比如，這里的影視劇作品）。將這種關系定義為成“隱式關聯”，LeaderRank算法也都沒有考慮數據集中存在的“隱式關聯”。為保留“隱式關聯”對意見領袖排名的影響，會在實驗前的數據整理過程中，將其顯式表示出來（即顯式的添加邊A→B和邊A→C，并在計算A與B、C的情感傾向時，將此評論計算進去）。

3.3.2 惡意注冊用戶

除了考慮用戶間的情感傾向外，需注意到網絡中存在的一定數量的惡意注冊用戶，例如微博中出現的“僵尸粉”。“僵尸粉”通常由第三方系統自動產生。如圖2所示，第二、三、四條評論即是惡意注冊用戶對某微博進行惡意評論的情況。

圖2 某微博惡意評論圖

這種惡意注冊用戶在現實網絡中，并不對信息進行傳播或阻礙，因此在挖掘意見領袖時，將這種惡意注冊用戶也計算進去是不恰當的。雖然在LeaderRank算法以及加權LeaderRank算法中，通過添加“Ground Node”可以讓惡意注冊用戶的更多分數流入“Ground Node”，但是惡意注冊用戶始終還是存在分數流入其他信息源的情況，當這種惡意注冊用戶足夠多時，會影響到意見領袖的排名，從而影響意見領袖挖掘的準確性。

3.4 改進的LeaderRank算法

針對上述LeaderRank算法存在的缺陷，本文做出了如下改進。

3.4.1 添加用戶情感傾向

從圖1中可以得到，微博內容主要是由文本、表情符合以及“贊”標志個數構成，微博內容的情感傾向也主要由這三部分的情感傾向組成。為簡單起見，本文使用“贊”標志個數表示微博的情感傾向，其計算公式如式（4）所示：

其中，μij表示節點i對節點j發布的某條回復（或微博）的感情傾向得分；δ表示此回復的“贊”的個數；lgδ是此條回復的“贊”標志的得分。

在確定網絡中任意兩個用戶α和β之間的情感傾向時，并不是取決于α和β之間的某次回帖的情感傾向，而是由特定時間段內，α和β之間全部回帖的情感傾向的平均值決定的。ρij表示節點i與節點j之間的“平均情感傾向”，其計算公式如式（5）所示：

其中，μij表示在t時刻節點i對節點j回復的情感傾向得分，共計n個時刻。

3.4.2 減弱惡意注冊用戶的影響

通過對微博等社交網絡的觀察，發現惡意注冊用戶與非活躍用戶之間存在很大交集，因此本文使用時間衰減的方式來限制惡意注冊用戶對意見領袖挖掘的影響。衰減比例公式如式（6）所示：

其中，tl表示用戶i最后一次有效操作的時間（例如，發帖、發表評論、轉帖等操作）；D是衰減指數；E是阻尼系數；θi(tc)表示的是節點i在tc時刻的衰減比例。

3.4.3 算法的改進

本文將用戶之間的情感傾向、時間衰減因素與加權LeaderRank算法結合，改進的LeaderRank算法核心公式如式（7）所示：

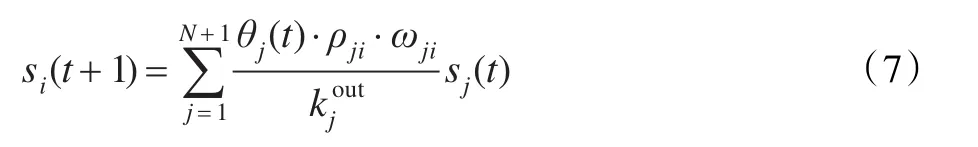
其中，ωij為一條邊的權重值，取值規則為：若j為“Ground Node”，ωig=1，ωgi=；若不存在i指向j的邊，ωij=0；其余情況ωij=1。ρji為式（4）中得到的節點i與節點j之間的情感傾向值。θj(t)為式（5）式中得到的節點j在t時刻的衰減比例；其他變量含義同公式（1）、（2）。

4 實驗及分析

實驗模型：實驗采用Susceptible-Infected-Removed（SIR）模型[19]，該模型由Kermack與McKendrick在1927年提出，直到現在SIR模型仍被廣泛使用。在SIR模型中，用N(t)表示t時刻的總人數，總人口分為以下三類：易感者（Susceptibles），記為S(t)，表示t時刻未染病但有可能被該類疾病傳染的人數；染病者（Infectives），記為I(t)，表示t時刻已被感染成為病人而且具有傳染力的人數；移出者（Removal），記為R(t)，表示t時刻已從染病者中移出的人數。在實驗過程中發現，將SIR模型中的康復免疫概率γ設置成1，感染概率β設置成0.02時，效果較好。

數據準備：實驗使用的數據集為新浪微博在2013年8月到12月份中對某一熱門話題的討論數據。由于新浪微博API存在接口訪問頻次等限制，所以實驗并沒有使用新浪API獲取實驗數據，而是使用課題組實現的頁面爬蟲工具進行抓取，再將得到的原始數據進行整理，除去新浪微博活動、廣告等非用戶發布的信息，并且將上文提到的“隱式關聯”顯式表示出來。數據整理后，共計67 031個節點，130 122條邊。

參數分析：在上述公式（6）中，參數D的取值對減弱惡意用戶的影響有重要作用。若D取值過大，則減弱惡意用戶影響力的效果不明顯；若D取值過小，則會影響正常用戶中，短時間未活動用戶的影響力。

下面通過實驗確定參數D較合適的取值。考察對于D的不同取值，改進LeaderRank得到前5名的意見領袖的所影響的用戶個數的平均值。從圖3中可以得到，當D取值在區間[0.8，0.9]之間較合適。

圖3 參數D取值測試圖

4.1 準確性比較

以PageRank算法和LeaderRank算法為對照組，實驗驗證改進LeaderRank算法的準確性。在上述數據集中，分別應用上述3種算法找到的排名前20的意見領袖，實驗結果數據如表1所示。

表1 排名前20的意見領袖對比表

表1第一行第二列表示應用LeaderRank算法得到的排名第一的意見領袖為“id=13423”號用戶，其他列以此類推。由實驗結果整理可得，LeaderRank算法得到的前20名中的{1207，517，31241}號意見領袖無法由其他兩種算法得到。同理，PageRank算法得到的{37，517，143}和改進LeaderRank算法得到的{1207，544，31241}無法由其他兩種算法得到。針對表1中的數據，專門查看了造成此差異的具體原因，以“id=517”號用戶為例，在LeaderRank算法的結果中排名為第5，在改進Leader-Rank算法的結果中排名為第151。這里發現其微博的粉絲和評論很多，但是相當一部分都是反對其觀點的評論，并且其微博“贊”個數幾乎沒有，如圖4所示。

圖4 反對評論示例圖

接著，給這些只由單一算法得到的意見領袖施加影響，觀察一段時間內，受這些意見領袖影響的其他用戶的人數，由此判定這些意見領袖的影響力，作為衡量“意見領袖挖掘”算法準確性的度量標準。實驗得到的前20位意見領袖，即Top-20曲線如圖5（a）所示。出于實驗的嚴謹考慮，同時實驗Top-50曲線和Top-100曲線，分別如圖5（b）和5（c）所示。橫坐標表示迭代時間t，縱坐標表示被影響的節點個數N，PageRank算法的c取0.15；以30次實驗平均值度量實驗結果。

由圖5可以看出，改進的LeaderRank算法挖掘出的意見領袖的影響力略高于LeaderRank算法，但收斂速度比LeaderRank算法慢一些，故而適用于對精度要求更高而對時間消耗要求相對較寬松的場合。

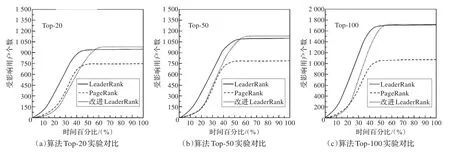
圖5 3種算法Top-N實驗對比圖

4.2 抗干擾能力比較

下面設計實驗，比較3種算法的抗干擾能力。在網絡中添加一定數量的惡意注冊用戶，并將這些惡意注冊用戶隨機與圖中節點相連，并隨機對相連節點的微博進行回復操作和“點贊”操作。比較添加惡意用戶之后各節點排名與添加惡意用戶之前各節點排名，變化較小的即被認為是抗干擾能力強的。抗干擾能力公式，如公式（8）所示：

其中，S′i表示添加惡意注冊用戶前，i節點的得分；S′i表示添加惡意注冊用戶后，j節點的得分。

實驗對排名前100的意見領袖施加干擾，3種算法下的抗干擾能力結果如圖6所示，越接近對角線則認為其抗干擾能力越強。實驗結果證明，改進的LeaderRank算法的抗干擾性優于LeaderRank算法和PageRank算法。

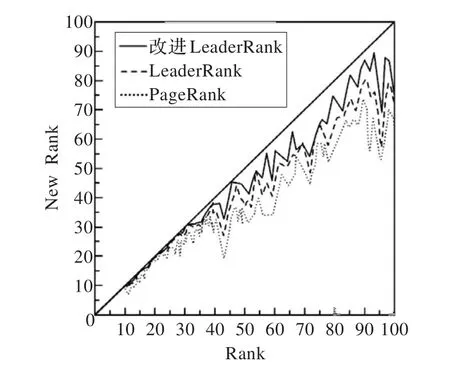
圖6 3種算法穩定性對比圖

5 結束語

“意見領袖挖掘”在社會網絡研究領域是一個重要的研究課題。本文的主要貢獻在于：通過將網絡中用戶之間的情感傾向、用戶活躍程度與LeaderRank算法相結合，對LeaderRank算法進行改進，提高了LeaderRank算法的準確性和抗干擾能力。但是，改進后的LeaderRank依然存在不足，例如微博內容的情感傾向沒有考慮文本以及表情符號的情感，這將是下一階段的研究重點。

[1]Zhou T，Fu Z Q，Wang B H.Epidemic dynamics on complex networks[J].Progress in Natural Science，2006，16（5）：452-457.

[2]Lv L，Chen D B，Zhou T.The small world yields the most effective information spreading[J].New Journal of Physics，2011，13（12）.

[3]Doerr B，Fouz M，Friedrich T.Why rumors spread so quickly in socialnetworks[J].Communications ofthe ACM，2012，55（6）：70-75.

[4]Schl?pfer M，Buzna L.Decelerated spreading in degreecorrelated networks[J].Physical Review E，2012，85（1）.

[5]Aral S，Walker D.Identifying influential and susceptible members of social networks[J].Science，2012，337：337-341.

[6]Bai W J，Zhou T，Wang B H.Immunization of susceptibleinfected model on scale-free networks[J].Statistical Mechanics and its Applications：Physica A，2007，384（2）：656-662.

[7]Hébert-Dufresne L，Allard A，Young J G，et al.Global efficiency of local immunization on complex networks[R].Scientific Reports，2013.

[8]Zhou Y B，Lv L，Li M.Quantifying the influence of scientists and theirpublications：distinguishing between prestige and popularity[J].New Journal of Physics，2012，14（3）.

[9]Park J，Newman M E J.A network-based ranking system for US college football[J].Journal of Statistical Mechanics：Theory and Experiment，2005（10）：10014.

[10]Huang X，Vodenska I，Wang F，et al.Identifying influential directors in the United States corporate governance network[J].Physical Review E，2011，84（4）.

[11]Kitsak M，Gallos L K，Havlin S，et al.Identification of influential spreaders in complex networks[J].Nature Physics，2010，6（11）：888-893.

[12]Katz L.A new status index derived from sociometric analysis[J].Psychometrika，1953，18（1）：39-43.

[13]Dolev S，Elovici Y，Puzis R.Routing betweenness centrality[J].Journal of the ACM，2010，57（4）.

[14]Estrada E，Rodriguez-Velazquez J A.Subgraph centrality in complex networks[J].Physical Review E，2005，71（5）.

[15]Kim H J，Kim J M.Cyclic topology in complex networks[J].Physical Review E，2005，72：1-4.

[16]Song K，Wang D，Feng S，et al.Detecting opinion leader dynamicallyinChinesenewscomments[M]//Web-Age Information Management.Berlin Heidelberg：Springer，2012：197-209.

[17]Lv L，Zhang Y C，Yeung C H，et al.Leaders in social networks，the delicious case[J].PloS One，2011，6（6）.

[18]Li Q，Zhou T，Lv L，et al.Identifying influential spreaders by weighted LeaderRank[J].Physica A，2014，404：47-75.

[19]Anderson R M，May R M，Anderson B.Infectious diseases of humans：dynamics and control[M].Oxford：Oxford University Press，1992.