RCC8的一致分割及其算法

崔文正

中國(guó)科學(xué)院 數(shù)學(xué)與系統(tǒng)科學(xué)研究院，北京 100190

1 引言

區(qū)域連接演算（Region Connection Calculus，RCC）是一種用來(lái)進(jìn)行空間定性表示和推理的形式化模型[1]。而RCC8是區(qū)域連接演算中最常用的一個(gè)子集。RCC[1]最早由Randell等人于1992年基于Clarke利用二元連接關(guān)系公理化分體拓?fù)鋵W(xué)（Mereotopology）的工作提出[2-3]，迄今20年取得了一系列重要的理論和應(yīng)用成果，研究?jī)?nèi)容包括：RCC及其子集的推理可判定性[4-6]；基于認(rèn)知的RCC評(píng)價(jià)[7-8]；RCC推理的復(fù)雜度[9-10]；拓?fù)鋸?fù)合表分析[11]和拓?fù)潢P(guān)系擴(kuò)展[12-13]；集成多種空間、方向、時(shí)間、位置等信息的定性推理[14-17]等。

RCC8規(guī)定了兩個(gè)空間區(qū)域間可能的八種基本關(guān)系。這些關(guān)系是DC（相離）、EC（外切）、EQ（相等）、PO（部分重合），TPP（內(nèi)切）和它的逆關(guān)系TPP-1，NTPP（真包含）和它的逆關(guān)系NTPP-1，圖1是這幾種關(guān)系的示意圖。這八種關(guān)系兩兩不相交，并且覆蓋了區(qū)域之間所有可能的關(guān)系，這種性質(zhì)的關(guān)系被稱為JEPD（Jointly Exhaustive and Pairwise Disjoint）關(guān)系，或者基關(guān)系。因?yàn)榭臻g中任何兩個(gè)區(qū)域的關(guān)系只可能是其中的一種，所以可以用基關(guān)系來(lái)表示兩個(gè)空間區(qū)域之間確定的知識(shí)，而不確定的知識(shí)則可以用可能的關(guān)系的析取來(lái)表示。

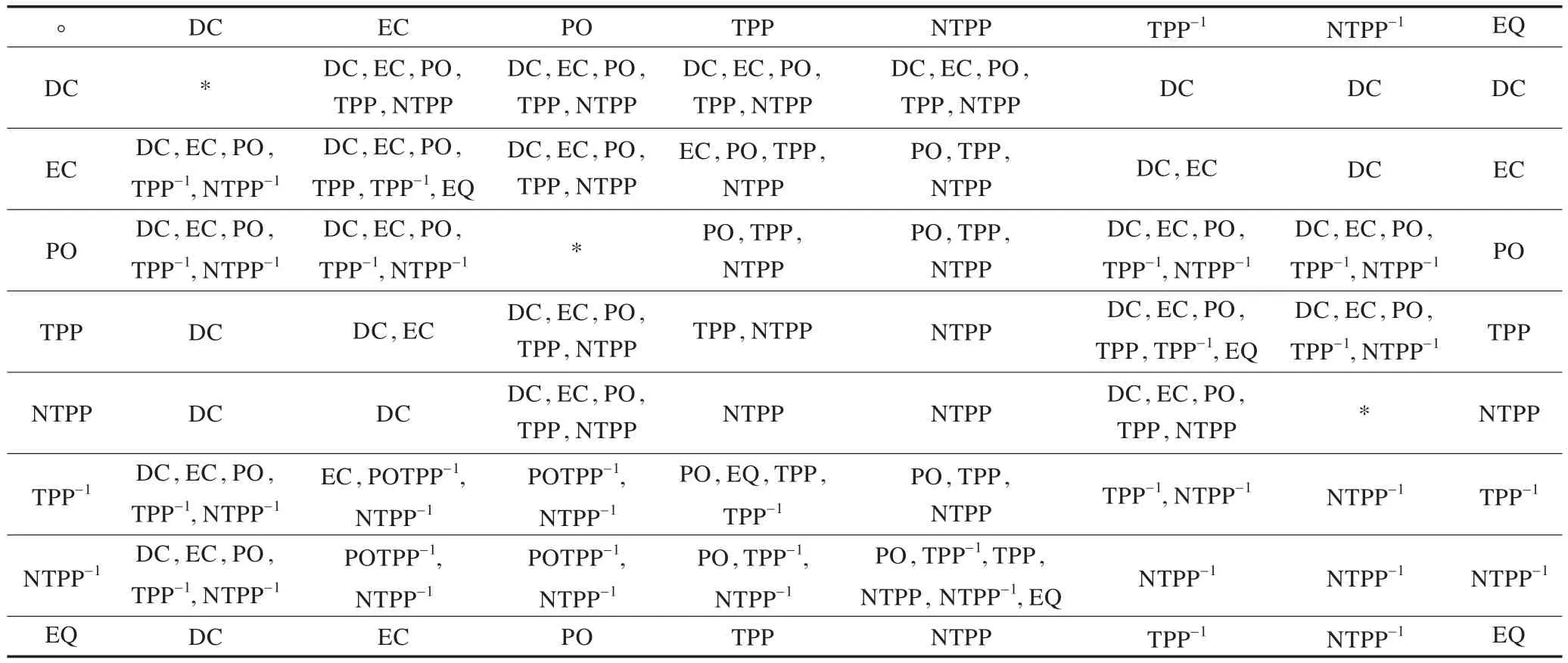
表1 RCC8復(fù)合運(yùn)算表

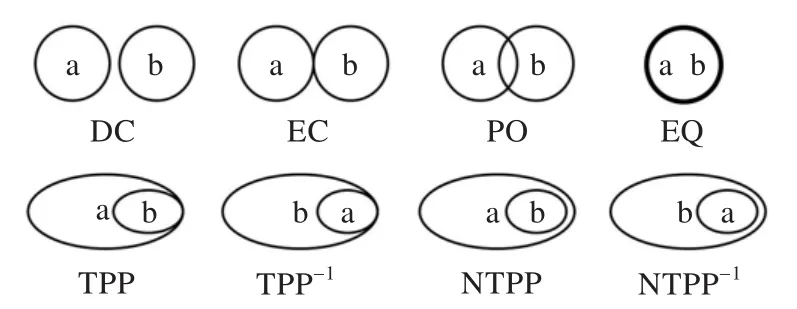
圖1 RCC8示意圖

表1表示的是RCC8的基關(guān)系復(fù)合運(yùn)算(·)表[18]，表中的項(xiàng)目是行與列中基關(guān)系的復(fù)合結(jié)果。如三個(gè)區(qū)域x、y、z，x和y關(guān)系為TPP，y和z的關(guān)系為EC，由表中TPP和EC的復(fù)合結(jié)果，可以得到x和z的關(guān)系可能是DC或者EC。*代表全關(guān)系，所有基關(guān)系的析取。

用約束來(lái)指定某兩個(gè)空間區(qū)域間為某個(gè)關(guān)系。RCC8的約束網(wǎng)絡(luò)由一個(gè)有限的空間區(qū)域集合和該集合上有限的約束集合構(gòu)成[19]。如果兩個(gè)空間區(qū)域在約束網(wǎng)絡(luò)中沒(méi)有約束，那么就認(rèn)為它們的約束是全關(guān)系。為了方便使用圖論的定理和結(jié)果，定義了一種圖結(jié)構(gòu)來(lái)描述約束網(wǎng)絡(luò)，稱為約束圖（見(jiàn)2.1節(jié)）。

如果有r?R，稱關(guān)系r是R的細(xì)化（refinement）。如果約束圖G′與G有相同的頂點(diǎn)集合，且對(duì)于任兩個(gè)頂點(diǎn)在G′中的約束關(guān)系r和在G中的約束關(guān)系R，都有r?R，稱G′是G的一個(gè)細(xì)化[18]。

一個(gè)給定的約束圖G是一致的就意味著存在另一個(gè)約束圖G′是G的細(xì)化，并且G′中所有頂點(diǎn)之間的約束都是基關(guān)系。G′也被稱為G的一個(gè)一致解。一般求解約束圖的一致性是一個(gè)NP問(wèn)題，要用回溯法求解，復(fù)雜度是指數(shù)級(jí)的。

路徑一致性是一致性的一個(gè)必要條件，它只要求約束圖中任何三個(gè)區(qū)域構(gòu)成的約束圖都是一致的。路徑一致性算法的時(shí)間復(fù)雜度是O(n3)[10]，將路徑一致性算法的運(yùn)行結(jié)果稱為路徑一致性解。RCC8可處理子集指的是可以在多項(xiàng)式時(shí)間內(nèi)求解一致性的RCC8關(guān)系集合，如果將約束關(guān)系限制在RCC8的可處理子集、C8或Q8的話，路徑一致性和一致性等價(jià)[9]。

現(xiàn)有的定性空間推理機(jī)有GQR[20]、PelletSpatial[21]、PyRCC8-?[22]。首先利用路徑一致性算法對(duì)約束圖進(jìn)行路徑一致性檢查，然后對(duì)路徑一致性解使用回溯法進(jìn)行一致性判定。

對(duì)大型約束圖，求一致性解的回溯法代價(jià)太高，即便是路徑一致性算法，O(n3)的時(shí)間復(fù)雜度也是較高的。為了解決大型、稀疏的約束圖的一致性檢查問(wèn)題，Huang證明了對(duì)于RCC8的可處理子集有Patchwork的性質(zhì)[23]。Sioutis和Koubarakis利用Patchwork性質(zhì)將約束圖三角化，以此提高路徑一致性推理效率[22]。Li和Huang等人討論了區(qū)間代數(shù)（IA）和RCC分解的方法[24-25]，但是這些工作只對(duì)關(guān)系全部為基關(guān)系的約束圖有效。

本文從圖論中的割和割集的概念出發(fā)，提出一致分割的概念。目標(biāo)是在保持一致性的條件下，將一個(gè)約束圖G分割成若干個(gè)不相交的子圖，通過(guò)檢查規(guī)模較小的子圖的一致性來(lái)判斷G的一致性，以此降低一致性檢查時(shí)間。第2章介紹了約束圖、分割、Patchwork等的基礎(chǔ)知識(shí)，并基于此提出了一致分割的定義及其成立的充分必要條件。第3章給出了兩個(gè)一致分割的充分條件和基于這兩個(gè)充分條件的高效的一致分割算法。第4章采用隨機(jī)生成的大型稀疏約束圖進(jìn)行實(shí)驗(yàn)，驗(yàn)證了一致分割算法的有效性。

2 一致分割

本章介紹文章的主要內(nèi)容：約束圖的一致分割的定義和充分必要條件。這主要源自于圖論中的割的概念和RCC8的Patchwork[23]性質(zhì)。

2.1 約束圖

可以用約束圖來(lái)表示RCC8的約束網(wǎng)絡(luò)。一般情況下，約束圖應(yīng)該是一個(gè)有向圖。頂點(diǎn)v代表空間區(qū)域，而v1，v2之間的有向邊則代表v1，v2的約束。但如果經(jīng)過(guò)一步預(yù)處理，也可以使用無(wú)向圖來(lái)表示約束網(wǎng)絡(luò)。

對(duì)任一個(gè)約束網(wǎng)絡(luò)都可以做如下預(yù)處理。假設(shè)約束網(wǎng)絡(luò)中vi，vj的約束為R，vj，vi的約束為Q：若Q和R不互逆，則將vi，vj的約束賦為R∩Q-1，vj，vi的約束賦為Q∩R-1，這樣使vi，vj和vj，vi的約束互逆；若Q=R=*（全關(guān)系），則刪除vi，vj和vj，vi的約束。顯然，經(jīng)過(guò)預(yù)處理的約束網(wǎng)絡(luò)仍與原約束網(wǎng)絡(luò)等價(jià)。經(jīng)過(guò)預(yù)處理就可以用無(wú)向圖來(lái)描述約束網(wǎng)絡(luò)。

定義1（約束圖）約束圖G=(V，E)是一個(gè)無(wú)向圖，V，E分別是圖的頂點(diǎn)集和邊集，有V={vi|0≤i≤n}，E={(vi，vj，R)|0≤i＜j≤n，(vi，vj)∈R，(vj，vi)∈R-1} 。約束圖中沒(méi)有邊連接的頂點(diǎn)對(duì)(vi，vj)表示有約束(vi，vj)∈*成立，*為全關(guān)系。

定義2（分割和割集）約束圖G=(V，E)的分割S=(G1，G2)，其中Gk=(Vk，Ek)，V1∩V2= ? ，Ek={(vi，vj，R)∈E|vi，vj∈Vk} ，k=1，2 。 割 集Scut={(u，v，R)∈E|u∈G1，v∈G2}。

定義3（橋）橋是割集元素?cái)?shù)為1的分割。

定義4（誘導(dǎo)子圖）對(duì)于約束圖G=(V，E)和其子圖H=(V1，E1)，如果V1?V，有E1={(vi，vj，R)∈E|vi，vj∈V1}，那么稱H為G的誘導(dǎo)子圖，記為H=GV1。

值得注意的是誘導(dǎo)子圖的這個(gè)表示方法將在與Patchwork相關(guān)的工作中被頻繁用到，它代表的含義就是由圖G中一部分頂點(diǎn)和這些頂點(diǎn)在G所有邊構(gòu)成的子圖。另外，VG代表圖G的頂點(diǎn)集合。

2.2 Patchwork

Patchwork性質(zhì)：如果兩個(gè)一致的約束圖的一致解在共有的頂點(diǎn)上的約束是相同的，那么這兩個(gè)約束圖的并依然是一致的[23]，如定義5所描述。

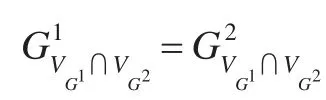
RCC8一致性檢查是一種約束滿足問(wèn)題，而且基于RCC8的可處理子集8，C8，Q8的一致性問(wèn)題是有Patchwork性質(zhì)的[23]。在下文中如無(wú)特殊說(shuō)明，討論范圍都限定于RCC8可處理子集。

2.3 一致分割及其成立條件

為了描述這種保持一致性的分割，給出一致分割的定義：

定義6（一致分割）一個(gè)約束圖G的分割是一個(gè)一致分割，當(dāng)且僅當(dāng)分割成的兩個(gè)子約束圖G1，G2的一致性與G的一致性等價(jià)。

可以知道G如果是一致的，那么必然存在一個(gè)解S，可知分別是G1，G2的解。所以容易推出一致分割的等價(jià)描述。

推論1對(duì)于一個(gè)分割，如果分割的兩個(gè)子約束圖G1，G2是一致的則G也是一致的，那么這個(gè)分割是一個(gè)一致分割。

由于在可處理子集中，約束圖的路徑一致性和一致性是等價(jià)的，可以結(jié)合RCC8可處理子集的Patchwork性質(zhì)得到一致分割的充分必要條件：

定理1 約束圖G=(V，E)的分割S={G1，G2}，割集為Scut，記。S是一致分割的充分必要條件是：Gs，G1，G2都是路徑一致的且對(duì)于Gs，G1，G2的路徑一致性 解Gs*，G1*，G2*有。

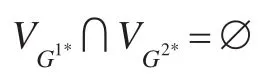
由于Gs*，G1*，G2*是Gs，G1，G2路徑一致性解，那么G1∪G2∪Gs滿足一致性，則G一致性得證。則由推論1知S為一致分割。

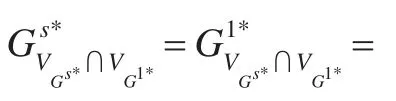
推論2約束圖G如果含有若干個(gè)連通分量，那么所有連通分量的一致性和G的一致性等價(jià)。

這個(gè)推論的另一個(gè)等價(jià)描述是：

推論3如果約束圖的割集為空集，這個(gè)分割是一致分割。

3 一致分割算法

從上文可知，如果割集中所有頂點(diǎn)的誘導(dǎo)子圖的路徑一致性解和其他兩個(gè)分割后的子圖的解滿足定理1的條件，就可以得到約束圖的一致性。

本章主要討論這個(gè)定理的應(yīng)用方法。3.1節(jié)給出了尋找一致分割的算法，并分析此算法的性能。為了提高約束圖一致分割的效率，3.2節(jié)給出了兩種一致分割的充分條件，和相應(yīng)的高效分割算法。

3.1 一致分割尋找算法

一般的，可以通過(guò)檢查約束圖的所有分割，利用定理1篩選出該約束圖的所有一致分割。

一致分割尋找算法：

輸入：約束圖G

返回：一致分割集合Pc

1.P←{pi|pi為G的一個(gè)分割}

2.Pc←?

3.當(dāng)P不是空集時(shí)：

4. 從P中選取分割pi，并將其從P中刪除

5. 利用定理1檢查pi是不是一致分割

6.pi是一致分割：將pi加入Pc

7.返回Pc

從定理1的特點(diǎn)和這個(gè)算法的過(guò)程可以看出直接使用這個(gè)一致分割尋找算法有以下兩個(gè)問(wèn)題：

（1）一個(gè)圖的分割個(gè)數(shù)至少是(2n-1-1)個(gè)，所以這個(gè)算法至少也是指數(shù)級(jí)的。顯然這并不是一個(gè)實(shí)用的算法。

（2）充分必要條件不僅要求出分割的兩個(gè)子圖的路徑一致性解，也要求出割集相關(guān)的頂點(diǎn)在G里的誘導(dǎo)子圖H的路徑一致性解。如果求解H消耗的時(shí)間超過(guò)了分別進(jìn)行一致性求解節(jié)約的時(shí)間，一致分割就無(wú)法減少總時(shí)間消耗了。

3.2 一致分割成立的充分條件

這一節(jié)給出充分條件來(lái)尋找一致分割。這些條件的缺點(diǎn)是不能如一致分割尋找算法找出任何一個(gè)圖所有的一致分割，但是對(duì)某些圖它們能高效地找到某些特殊的一致分割。在處理稀疏圖或者滿足一些特定結(jié)構(gòu)的圖的時(shí)候，這些條件和其相對(duì)應(yīng)的算法就非常有用。

3.2.1 橋分割

對(duì)于割集為橋的分割，有著如下定理所述的性質(zhì)：

定理2約束圖中如果存在著橋，那么以這個(gè)橋作為割集的分割是一個(gè)一致分割。

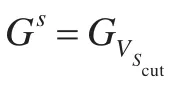
這個(gè)結(jié)論可以使用Tarjan在1974年提出的Bridge-Finding算法[26]，在O(|E|+|V|)的時(shí)間內(nèi)找出所有的橋，將這些橋從約束圖G中去除后所有連通分量的一致性和G的一致性是等價(jià)的，得到所有連通分量的算法時(shí)間復(fù)雜度也是O(|E|+|V|)。這樣完成一次約束圖關(guān)于橋的一致分割的時(shí)間復(fù)雜度也為O(|E|+|V|)。

3.2.2 弱關(guān)系分割

先給出弱關(guān)系的定義：

定義7（弱關(guān)系）RCC8中，如果存在一個(gè)基關(guān)系r滿足如下條件，就定義這個(gè)r為一個(gè)弱關(guān)系：

（1）r=r-1；

（2）?R，r?R·r；

（3）?R，r?r·R；

（4）r·r=*。

注：其中R代表任意一個(gè)RCC8關(guān)系，*代表全關(guān)系。

定理3約束圖的割集Gs所有約束中出現(xiàn)的關(guān)系集合記為RS，r為RCC8中的某個(gè)弱關(guān)系。如果?R∈RS，r?R，那么這個(gè)分割是一個(gè)一致分割。

證明G1，G2都滿足一致性，則一定存在一致解G1*，G2*，每個(gè)空間之間的關(guān)系都是基關(guān)系，那么需要證明G是一致的。有?R∈RS:r?R成立，那么RS′是RS的一個(gè)細(xì)化，其中RS′所有的約束關(guān)系都可以細(xì)化為r（因?yàn)槊總€(gè)關(guān)系都包含r）。證明G*=G1*∪G2*∪Gs*是一個(gè)G的一致解。

因?yàn)镚*只是由基關(guān)系構(gòu)成的約束集合，那么可以用檢查路徑一致性確定G*是否一致。可以任取三點(diǎn)a，b和c∈，列舉所有可能的路徑。

（1）?i=1，2:a，b，c∈：三者之間的約束同在Gi*，由Gi*一致性易知路徑一致。

（2）三個(gè)空間不同在一個(gè)空間集合，不失一般性假設(shè)：a∈，b∈，c∈。可以知道Rac，Rbc∈RS′，那么由r=r-1知道Rac=Rbc=Rca=Rcb=r，且有?R，r?R·r，r?r·R，r·r=R*。所以可以知道Rab無(wú)論為哪個(gè)基關(guān)系，都不會(huì)給這三個(gè)點(diǎn)構(gòu)成的任何一條路徑帶來(lái)不一致。由于選取三個(gè)點(diǎn)的一般性得知G*是一致的。

由于G*是G的細(xì)化，且G*中約束都為基關(guān)系，可知G*是G的一個(gè)一致解，G的一致性得證。由推論1知滿足定理3性質(zhì)的分割為一致分割。

注意，在定理3的證明中并沒(méi)有用到可處理子集的性質(zhì)，說(shuō)明定理3對(duì)于所有的RCC8約束圖都成立。

可以從復(fù)合運(yùn)算表中驗(yàn)證DC、PO都是弱關(guān)系。所以割集中的關(guān)系如果全都包含DC或者全都包含PO的話，這個(gè)分割就是一個(gè)一致分割。利用弱關(guān)系進(jìn)行判斷和分割的算法如下所示，其中遍歷算法采用廣度優(yōu)先搜索（BFS）或者深度優(yōu)先搜索（DFS）皆可，本文以深度優(yōu)先搜索為例。

弱關(guān)系分割：

深度優(yōu)先搜索（DFS）：

如上所示，分割算法與經(jīng)典的深度優(yōu)先搜索算法唯一的不同之處在于增加了第15行的判斷：弱關(guān)系分割算法將約束關(guān)系包含r的邊視為不連通。這樣使得SG中不同的分割子圖之間只有兩種可能，要么沒(méi)有邊相連，要么連接兩個(gè)子圖的邊的約束關(guān)系都包含r，根據(jù)定理3這個(gè)算法的正確性得證。

另外，由于增加的第15行只有O()1的復(fù)雜度，所以這個(gè)算法仍然和深度優(yōu)先搜索算法有著相同的復(fù)雜度。根據(jù)深度優(yōu)先搜索的相關(guān)結(jié)論[27]，可以得出弱關(guān)系分割算法復(fù)雜度也僅為O(|E|+|V|)。

3.2.3 橋分割和弱關(guān)系分割的關(guān)系

以上證明了兩種一致分割的充分條件，可以看出，這兩個(gè)條件是互相獨(dú)立的。在一個(gè)約束圖里面，可以采用幾種不同的分割條件去判斷約束圖是否是可分割的。

圖2給出了一種使用多種分割條件將約束圖分割至不能分割為止的流程。該方法先后使用不同的一致分割算法嘗試對(duì)約束圖進(jìn)行分割，直到分割結(jié)果不再滿足任何一個(gè)一致分割條件。

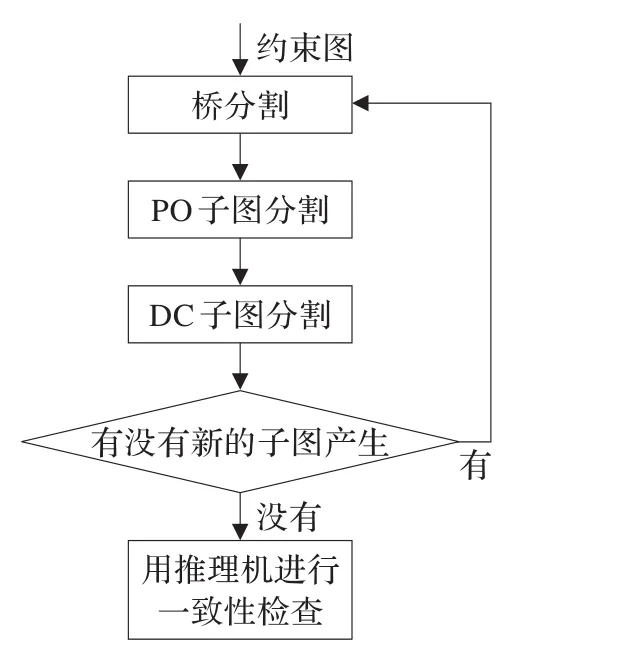
圖2 多分割條件一致分割流程圖

值得注意的是圖2中三種一致分割算法的調(diào)用順序不會(huì)改變最終分割結(jié)果。因?yàn)槿N算法都是將滿足某種條件的割集從約束圖G中刪除，而后將各個(gè)連通分量作為分割結(jié)果。假設(shè)調(diào)用一致分割條件順序?yàn)锳1→A2→…→An。如果Si是G滿足一致分割條件Ai的割集，使用A1，A2，…，Ai-1條件進(jìn)行分割的話有兩種可能：（1）Si中的一部分邊被A1，A2，…，Ai-1條件刪除，剩下的邊構(gòu)成集合S′i依然是滿足一致分割條件的割集；（2）A1，A2，…，Ai-1條件不會(huì)刪除Si中的邊。顯然，無(wú)論是哪一種情況這個(gè)一致分割條件Ai的分割效果都不會(huì)被影響。

然而，三種算法的調(diào)用順序?qū)τ谶\(yùn)行時(shí)間會(huì)有一定的影響。比如對(duì)于圖3，如果按照?qǐng)D2中的調(diào)用順序進(jìn)行分割的話，將進(jìn)行4次迭代才能將約束圖分割到不再可分。而采用DC子圖分割→ PO子圖分割→橋分割這樣的順序，就只用迭代兩次。

從三種分割的算法可以看出，約束圖G不能用同一個(gè)分割條件連續(xù)分割兩次。基于這個(gè)特點(diǎn)可以得到：

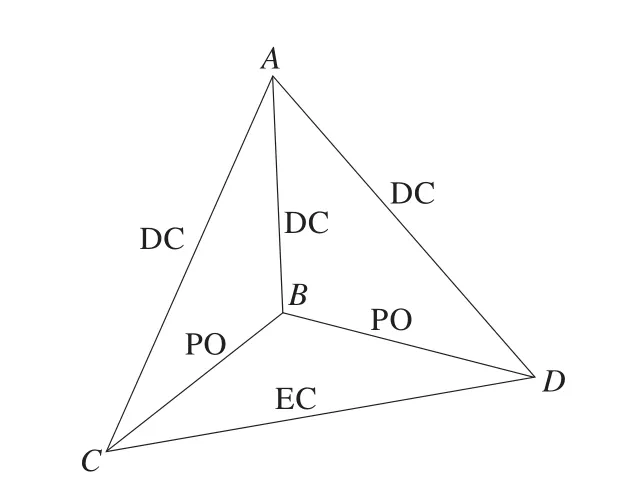
圖3 分割條件調(diào)用順序差異帶來(lái)運(yùn)行時(shí)間差異示例

定理4對(duì)于約束圖G，利用多分割條件一致分割時(shí)，若調(diào)用分割條件順序?yàn)锳1→A2→A3時(shí)，若G在某一次迭代中可以被Am分割，且不能被所有Ai(i＞m)分割，那么下一次迭代只可能：

（1）G不能用任何條件分割；

（2）存在某個(gè)條件Aj(j＜m)可以將其分割。

證明情況1，算法此時(shí)達(dá)到迭代終止條件。

情況2，首先一定存在一個(gè)條件可以分割G，否則就落到情況1中。不妨設(shè)第一個(gè)可以用來(lái)分割G的條件為Ak，首先k=m不可能成立，因?yàn)樯弦惠喌蠫被Am分割，其子圖不能被Am繼續(xù)分割；其次m＜k≤3也不能成立，這又與上一輪迭代中G不能被所有Ai(i＞m)分割相矛盾。所以必存在某個(gè)條件Aj(j＜m)可以將其分割。

從圖2中可以看出每次迭代的時(shí)間消耗是一定的，所以迭代次數(shù)越少，整個(gè)算法時(shí)間消耗就越小。

可以看出，降低迭代次數(shù)的關(guān)鍵在于增加每次迭代中成功分割的次數(shù)。

表2就是最壞情況的迭代示例。調(diào)用順序?yàn)锳1→A2→A3，且在Ai+1的分割成功之后才能使用Ai分割成功。表格中的行代表分割條件，列代表迭代輪次，其中的成功代表該輪次用對(duì)應(yīng)分割條件分割成功，如果某輪次中所有條件都未被成功調(diào)用就代表該約束圖已經(jīng)無(wú)法再進(jìn)行分割。可以看出，平均每次迭代成功分割次數(shù)約為1.5次。

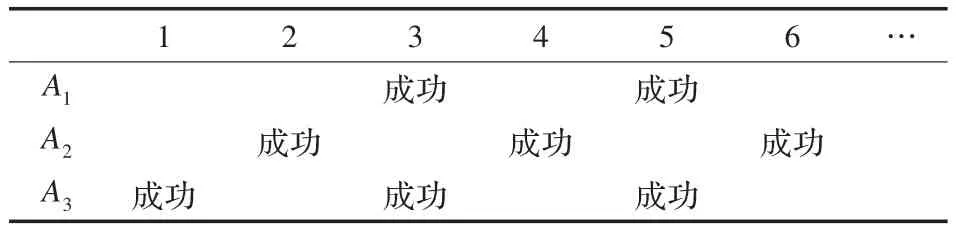
表2 最不利的迭代示例

而如果將調(diào)用的順序改為A3→A2→A1，如表3所示，之后的分割條件正好可以用上之前的分割結(jié)果，這樣平均每次迭代成功分割次數(shù)約為3次。由于成功分割順序是一樣的，兩次成功分割總次數(shù)相同，那么分割時(shí)間之比為2。每一次迭代的復(fù)雜度是O(|E|+|V|)，則最有利和最不利的總時(shí)間只差O(|E|+|V|)，可知調(diào)用順序?qū)λ惴ǖ男蕸](méi)有很大的影響。

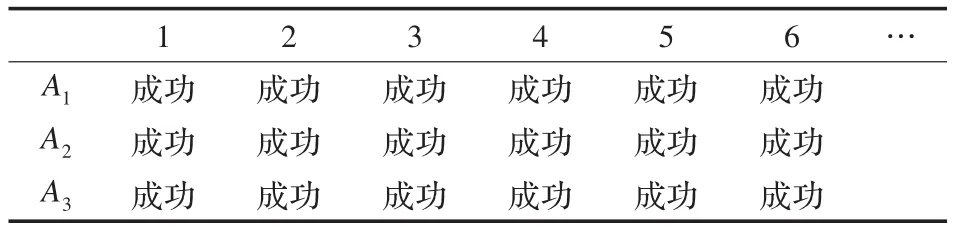
表3 最有利的迭代示例

4 實(shí)驗(yàn)

本章設(shè)計(jì)并進(jìn)行實(shí)驗(yàn)，用來(lái)驗(yàn)證以上提出的分割算法對(duì)于大型稀疏空間約束圖一致性檢查確實(shí)能夠起到提高效率的作用。

4.1 實(shí)驗(yàn)設(shè)計(jì)

在實(shí)驗(yàn)中用約束圖的邊數(shù)(E)和頂點(diǎn)個(gè)數(shù)(V)之商D=E/V的值來(lái)度量圖的稀疏程度，D稱為平均度。分別在D=0.5，1，2，3時(shí)，觀察約束圖的路徑一致性檢查時(shí)間和約束圖頂點(diǎn)個(gè)數(shù)的關(guān)系。約束圖是隨機(jī)生成的：限定約束圖的頂點(diǎn)個(gè)數(shù)為V(10 000～60 000)，在所有頂點(diǎn)對(duì)的集合中隨機(jī)取出E=V·D個(gè)項(xiàng)用邊相連，并從8中隨機(jī)選取關(guān)系作為邊的約束。

實(shí)驗(yàn)環(huán)境是：Intel Core i7-2600 CPU 3.40 GHz 8核，內(nèi)存20 GB，操作系統(tǒng)Fedora 15 64 bit，GCC 4.5.4；推理機(jī)采用GQR-1418[20]（同樣也可以采用其他的推理機(jī)進(jìn)行實(shí)驗(yàn)）。

4.2 實(shí)驗(yàn)結(jié)果

圖4～圖7分別表示在不同的平均度下，約束圖的路徑一致性算法運(yùn)行時(shí)間和約束圖頂點(diǎn)個(gè)數(shù)關(guān)系。其中灰柱代表直接用推理機(jī)對(duì)約束圖進(jìn)行路徑一致性檢查所用的時(shí)間，黑柱代表先利用一致分割進(jìn)行預(yù)處理后，推理機(jī)進(jìn)行路徑一致性檢查所用時(shí)間。沒(méi)有立柱代表推理機(jī)無(wú)法處理這個(gè)量級(jí)的約束圖。

從圖4和圖5中可以看出，在E/V≤1，即約束圖十分稀疏的時(shí)候，直接使用推理機(jī)是非常耗時(shí)而低效的；而且當(dāng)頂點(diǎn)個(gè)數(shù)多于一定量的時(shí)候（50 000），由于內(nèi)存限制，推理機(jī)不能夠繼續(xù)進(jìn)行。但是如果先進(jìn)行分割的話，不僅在很高的頂點(diǎn)個(gè)數(shù)時(shí)也能夠正常運(yùn)行，而且運(yùn)行時(shí)間也能一直維持在很低的水平上。

可以看出，隨著E/V值的增大，分割后的路徑一致性檢查運(yùn)行時(shí)間越來(lái)越接近直接進(jìn)行路徑一致性檢查的時(shí)間。在E/V=2時(shí)，分割算法依然有很高的效率提高作用，并且能完成直接檢查路徑一致性不能完成的任務(wù)；但是在E/V=3時(shí)候，分割算法已經(jīng)不能解決直接檢查無(wú)法處理的約束圖了，不過(guò)此時(shí)分割算法還是能夠帶來(lái)可觀的效率提高。

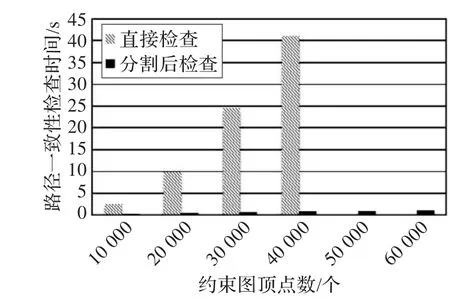
圖4 E/V=0.5時(shí)路徑一致性檢查時(shí)間和約束圖頂點(diǎn)數(shù)關(guān)系

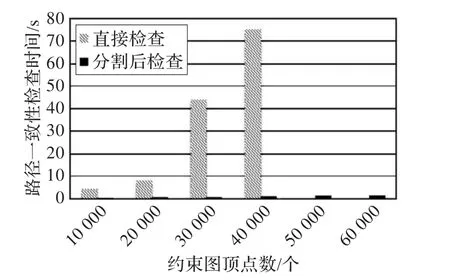
圖5 E/V=1時(shí)路徑一致性檢查時(shí)間和約束圖頂點(diǎn)數(shù)關(guān)系

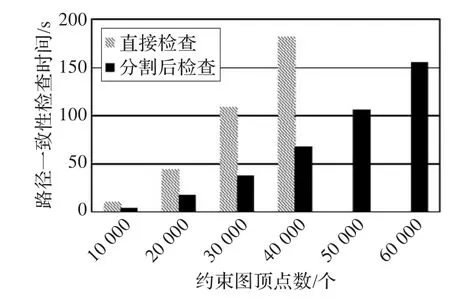
圖6 E/V=2時(shí)路徑一致性檢查時(shí)間和約束圖頂點(diǎn)數(shù)關(guān)系

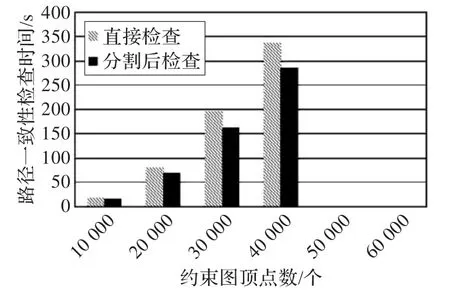
圖7 E/V=3時(shí)路徑一致性檢查時(shí)間和約束圖頂點(diǎn)數(shù)關(guān)系

從實(shí)驗(yàn)結(jié)果可以看出兩點(diǎn)：對(duì)大型的稀疏約束圖來(lái)說(shuō)，先進(jìn)行一致分割所帶來(lái)的效率提高是非常大的，這說(shuō)明本文提出的算法是有效的；隨著約束圖的密度上升分割算法帶來(lái)的效率提高會(huì)越來(lái)越小，這是由于一般情況下，越稠密的圖分割會(huì)越困難，這也表明了本文方法的局限性。

5 結(jié)論和工作展望

5.1 結(jié)論

本文給出了一致分割的概念，將空間約束圖的一致性檢查轉(zhuǎn)化為其一致分割子圖的一致性檢查。

一致分割可以作為RCC約束圖的一致性檢查推理機(jī)[2-4]的預(yù)處理過(guò)程。對(duì)于大型的、稀疏的RCC8約束圖一致性檢查，可以采用一致分割算法先對(duì)約束圖進(jìn)行分割，然后分而檢查子圖的一致性。本文方法具有以下幾個(gè)優(yōu)勢(shì)：

（1）一致分割算法時(shí)間復(fù)雜度為O(|E|+|V|)，遠(yuǎn)低于路徑一致性算法復(fù)雜度O(n3)。即便面對(duì)大型的約束圖，也可以用很小的時(shí)間代價(jià)去檢驗(yàn)這個(gè)圖是否可以分割。

（2）實(shí)驗(yàn)過(guò)程表明面對(duì)稀疏的約束圖，如果預(yù)先進(jìn)行一致分割處理，能夠大幅度減少總的時(shí)間消耗。

（3）對(duì)于一些由于內(nèi)存限制推理機(jī)無(wú)法處理的大型稀疏約束圖，一致分割算法能夠?qū)⑵浞指畛蔀槿舾蓪?duì)推理機(jī)來(lái)說(shuō)可處理的子圖，使得一致性檢查成為可能。

一致分割算法的弱點(diǎn)在于不能夠?qū)τ谒械募s束圖都起作用。對(duì)于不符合一致分割充分條件的約束圖，算法就無(wú)法為推理機(jī)提高效率了。

5.2 工作展望

一致分割算法還有著很多有待深入思考的問(wèn)題。首先是一致分割算法在真實(shí)數(shù)據(jù)中的效果。本文的實(shí)驗(yàn)數(shù)據(jù)是隨機(jī)生成的約束圖，對(duì)于真實(shí)數(shù)據(jù)是否仍有類似的結(jié)論是下一步要討論的問(wèn)題。例如RCC可以被用于地理信息的定性描述[28]。地理信息常常有著很強(qiáng)的層次結(jié)構(gòu)，比如洲、國(guó)家、省、市、縣等，由于高層級(jí)的區(qū)域之間（比如洲）的約束偏少，這也使得將描述地理信息的約束圖一致分割成為可能。

其次，可以將分割后各個(gè)子圖的一致性檢查過(guò)程并行化，因?yàn)檫@些過(guò)程是互相獨(dú)立的，所以并行運(yùn)算可以進(jìn)一步地提高一致性檢查的效率。

另外，一致分割也可以用來(lái)確定約束圖出現(xiàn)不一致的位置。若要找哪些區(qū)域之間的約束引入了不一致性，只需要檢查具有不一致性的分割子圖中區(qū)域之間的關(guān)系，而不需要去分析一致的子圖。

最后，尋找更多的一致分割條件和算法，對(duì)其他的基于JEPD關(guān)系的推理演算進(jìn)行一致分割的探索也都是未來(lái)研究的方向。

[1]Randell D A，Cui Zhan，Cohn A G.A spatial logic based on regions and connection[C]//Proceedings of the 3rd Inter-national Conference on Knowledge Representation and Reasoning.San Mateo，USA：Morgan Kaufmann，1992：165-176.

[2]Clarke B L.A calculus of individuals based on connection[J].Notre Dame Journal of Formal Logic，1981，22（3）：204-218.

[3]Clarke B L.Individuals and points[J].Notre Dame Journal of Formal Logic，1985，26（1）：61-75.

[4]Dornheim C.Undecidability of plane polygonal mereotopology[C]//Proceedings of the 6th International Conference on Principles of Knowledge Representation and Reasoning.[S.l.]：Morgan Kaufman，1998：342-353.

[5]Gotts N M.Using the RCC formalism to describe the topology of spherical regions，Technical Report 96.24[R].School of Computer Studies，University of Leeds，1996.

[6]Bennett B.Spatial reasoning with propositional logic[C]//Proceedings of the 4th International Conference on Knowledge Representation and Reasoning，1994：51-62.

[7]Knauff M，Rauh R，Renz J.A cognitive assessment of topological spatial relations：results from an empirical investigation[C]//Proceedings of the 3rd International Conference on Spatial Information Theory.Berlin：Springer，1997，1329：193-206.

[8]Renz J，Rauh R，Knauff M.Towards cognitive adequacy of topological spatial relations[C]//Proceedings of Spatial Cognition II.Berlin：Springer，2000，1849：184-197.

[9]Renz J.Maximal tractable fragments of the region connection calculus：a complete analysis[C]//Proceedings of the 16th International Joint Conference on Artificial Intelligence，Stocholm，Sweden.San Francisco，California，USA：Morgan Kaufmann Publisher Inc，1999：448-454.

[10]Renz J，Nebel B.Efficient methods for qualitative spatial reasoning[J].Journal of Artificial Intelligence Research，2001，15：289-318.

[11]Li Sanjiang，Ying Mingsheng.Region connection calculus：its models and composition table[J].Artificial Intelligence，2003，145（1/2）：121-146.

[12]Cohn A G，Bennett B，Gooday J，et al.Qualitative spatial representation and reasoning with the region connection calculus[J].GeoInformatica，1997（1）：1-44.

[13]歐陽(yáng)繼紅，富倩，劉大有.簡(jiǎn)單凹形區(qū)域間空間關(guān)系的一種表示及推理模型[J].電子學(xué)報(bào)，2009，37（8）：1830-1836.

[14]王生生，劉大有，謝琦.集成多方面信息的定性空間推理及應(yīng)用[J].軟件學(xué)報(bào)，2003，14（11）：1857-1862.

[15]陳娟，劉大有，賈海洋，等.基于MBR的拓?fù)洹⒎轿弧⒊叽缃Y(jié)合的定性空間推理[J].計(jì)算機(jī)研究與發(fā)展，2010，47（3）：426-433.

[16]Li Sanjiang.Combining topological and directional information for spatial reasoning[C]//Proceedings of the 20th International Joint Conference on Artificial Intelligence（IJCAI-07），2007：435-440.

[17]Liu Weiming，Li Sanjiang，Renz J.Combining RCC-8 with qualitative direction calculi：algorithms and complexity[C]//Proceedings of the 21st International Joint Conference on Artificial Intelligence（IJCAI-09），2009：854-859.

[18]Renz J.Qualitative spatial reasoning with topological Information[M].Berlin，Heidelberg：Springer-Verlag，2002.

[19]Bodirsky M，W?lfl S.RCC8 is polynomial on networks of bounded treewidth[C]//Proceedings of the 22nd International Joint Conference on Artificial Intelligence，2011：756-761.

[20]Gantner Z，Westphal M，W?lfl S.GQR—a fast reasoner for binary qualitative constraint calculation[C]//AAAI Workshop on Spatial and Temporal Reasoning，2008.

[21]Stocker M，Sirin E.PelletSpatial：a hybrid RCC-8 and RDF/OWL reasoning and query engine[C]//Proceedings of the 6th International Workshop on OWL：Experiences and Directions，Virginia，USA，2009.

[22]Sioutis M,Koubarakis M.Consistency of chordal RCC-8 networks[C]//Proceedings of the 24th IEEE International Conference on Tools with Artificial Intelligence，Athens，Greece，2012.

[23]Huang Jinbo.Compactness and its implications for qualitative spatial and temporal reasoning[C]//Proceedings of the 13th International Conference on Principles of Knowledge Representation and Reasoning，Rome，Italy，2012.

[24]Li Jason Jingshi，Huang Jinbo，Renz J.A divide-and-conquer approach for solving interval algebra networks[C]//Proceedings on 21st International Joint Conference on Artificial Intelligence，Pasadena，USA，2009：572-577.

[25]Huang Jinbo，Li Jason Jingshi，Renz J.Decomposition and tractability in qualitative spatial and temporal reasoning[J].Artificial Intelligence，2013，195：140-164.

[26]Tarjan R.A note on finding the bridges of a graph[J].Information Processing Letters，1974，2（6）：160-161.

[27]Cormen T H，Leiserson C E，Rivest R L，et al.Introduction to algorithms[M].[S.l.]：MIT Press，2001.

[28]Bennett B.The application of qualitative spatial reasoning to GIS[C]//Proceedings of the 1st International Conference on GeoComputation，1996：44-47.