地下水滲流的邊界元非重疊區域分解算法
田玲玲 祝家麟
(山西財經大學應用數學學院1) 太原 030006) (重慶大學數理學院2) 重慶 400030)
0 引 言
滲流問題是流體力學中的一個重要領域,也是巖土、水電工程設計中的重要課題之一.這類問題可歸結為Laplace方程(包括非齊次的)或Possion方程.邊界元法在滲流計算研究中有著廣泛的應用,用邊界元法研究滲流問題也比較早,20世紀70年代后期邊界元法得到了較快的發展.由于科學技術的迅猛發展,人們遇到了許多大規模的科學和工程計算問題,如何快速更有效的求解這些問題,成了工程技術人員和學者的一大難題.
區域分解算法是20世紀80年代崛起的新方向,由于該方法能將大型問題分解為小型問題﹑復雜邊值問題分解為簡單邊值問題﹑串行問題分解為并行問題,再加上并行計算機的出現和廣泛應用,這些問題得到了更有效的解決,區域分解算法作為并行計算和處理這類問題的主要方法,愈來愈受到人們的重視.
1 滲流問題描述及算法構造
根據水量守恒原理和達西定律[1-3]進行推導,考慮如下描述的滲流問題:
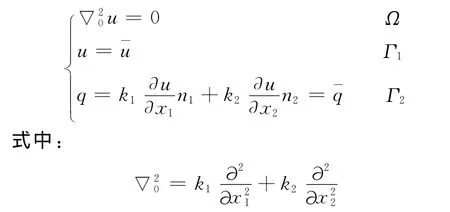
總邊界Γ1+Γ2,Γ1上位勢u已知,Γ2上是滲流量q已知,n1,n2分別是x1,x2方向上的余弦.k1,k2為滲透系數,并且滿足Q/A=kH/L.式中:Q/A為單位時間內滲過材料試件單位面結的水量;H/L為壓力水頭和滲透距離(試件的厚度)的比值.當介質是各向同性時,各個方向上k1,k2相等.
為簡明地說明該方法,僅討論將區域分解成2個非重疊區域的子區域[4]的情況(見圖1),假定區域Ω1,Ω2為正交各向異性介質滲流.計算步驟如下.
步驟1 首先任意給定公共邊界Γ0上的初始值u0(或q),設定循環控制誤差ε.
步驟2 在2個子區域上分別用直接邊界元法同時求解如下a和b 2個問題.

圖1 非重疊區域分解圖
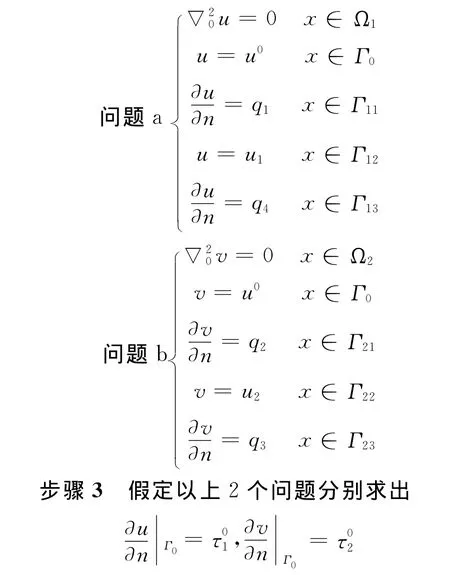
取τ0=+(1-α)(0<α<1)作為公共邊界上的新的已知條件,再次求解如下c和d問題:

步驟4 此時2個問題分別求出
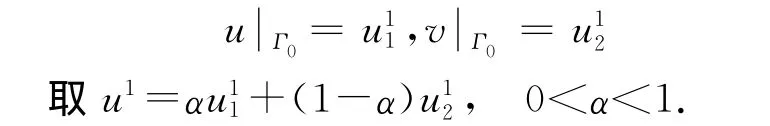
步驟5 若|u0-u1|<ε,停止計算,u1即為所求.否則重復重復上述步驟直到前后2次求得的值相差小于給定的ε.
步驟2和步驟5步利用通用的直接邊界元法求解,其邊界積分方程為

2 邊界積分方程的數值解法
用常單元離散求解[5],邊界積分方程為

按照常單元的特性,以每一單元上的節點之值u*,q*(i=1,2,…,n)代替單元上的值,即在每一單元上uj,qj是常量,則有
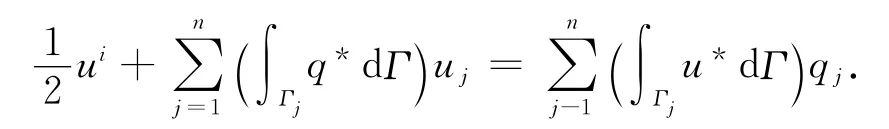
式中:u*,q*為基本解及其法向導數,它們在每一單元上的積分應視為已知.設

這就是離散后得到的代數方程組.內部點的位勢的離散形式為
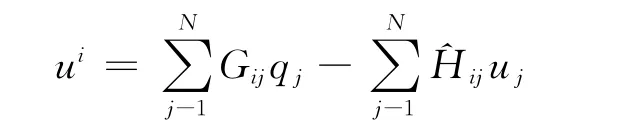
設(xi,yi)是i點坐標,(x,y)則是邊界上任一點的坐標.設u滿足Laplace方程,在Ω內及Γ上有連續一階導數.由是基本解[6],由u*的表達式知

要求解給出的線性方程組,必須求解上面推出的系數矩陣和右端項.
由
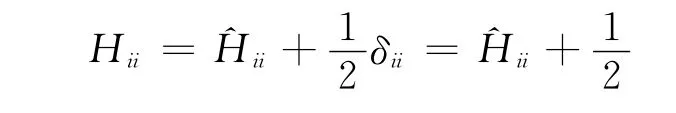
因為矢徑r的變化方向總是與Γi的法向n垂直,故^Hii=0,于是

如果設單元長度為Γi,則在量綱一的量坐標ξ下

式中:d為矢徑r在單位法向n方向上的投影,即為i點到單元Γj的距離;wm為給定的權,也稱求積系數.
非對角元Gij利用如下的解析法計算.

3 算 例
一個混凝土水壩如圖2所示,計算水壩下水經過2種介質的滲流,上層介質為均質的,下層介質為正交各向異性的,利用編制的非重疊區域分解邊界元程序計算公共層面的流速,繪制等勢線圖并與文獻[7]的等勢圖做比較.
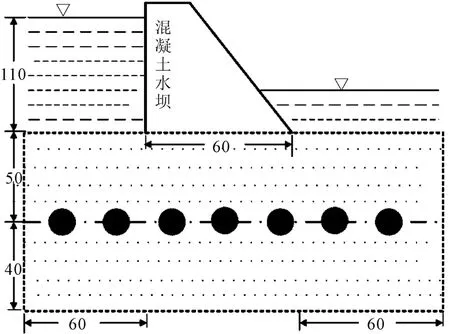
圖2 通過混凝土水壩底部的滲流圖(單位:m)
將研究區域分2個子區域,整個內外邊界劃分了70個常單元,計算結果見表1.
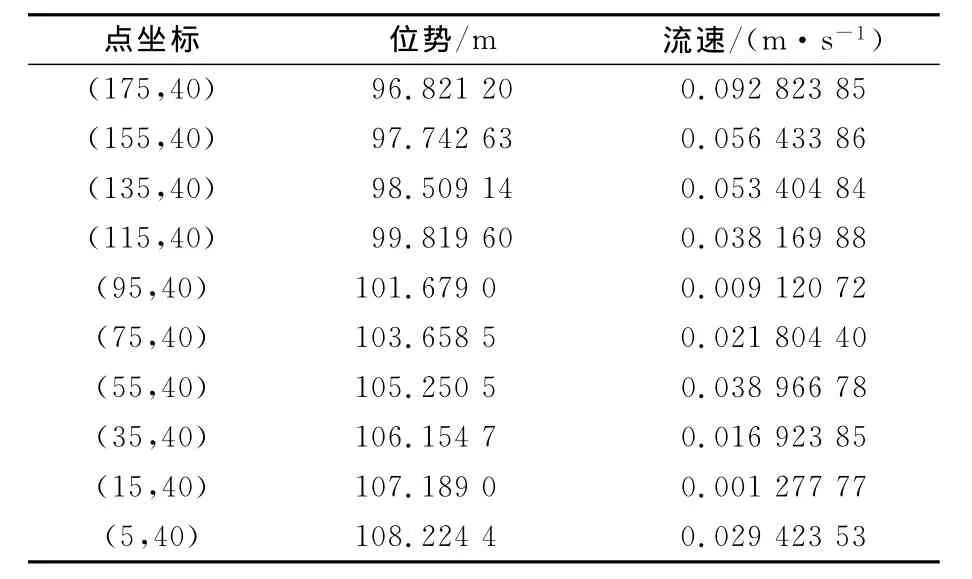
表1 公共邊界上若干點的計算結果
另外還可以畫出壩基等勢線如下圖3,圖中x軸為水壩底部橫向位置,y軸為水壩下層介質區域縱向位置.
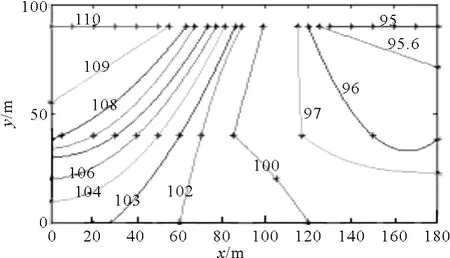
圖3 水壩基地等勢線圖
計算結果等勢線圖與文獻[7]的比較,可以看出基本吻合,說明本文所用方法是可行的.
4 結 論
本文就非重疊區域分解和邊界元結合起來用于求滲流方程做了一些嘗試,構造了求解滲流問題的邊界元非重疊區域分解的并行算法,最后利用自己編寫的程序,做了數值算例.得以下主要結論.
1)邊界元法需要準備的數據比較少,具有降維作用,可以解決奇異性問題特別適合解無限域問題以及遠場計算精度高等特點.
2)用邊界元法求解流體力學問題,因為不需要在內部剖分單元,程序處理一般比有限元法容易.
3)非重疊區域分解并行算法僅在邊界上交換數據,比有限元法簡單,該法直接利用這些邊界量作為子區域聯系的紐帶.
[1]張有天,王 鐳,陳 平.邊界元方法及其在工程中的應用[M].北京:水利電力出版社,1989.
[2]楊德全,趙忠生.邊界元理論及應用[M].北京:北京理工大學出版社,2002.
[3]錢孝星.水文地質計算[M].北京:水利電力出版社,1993.
[4]呂 濤,石濟民,林振寶.區域分解算法:偏微分方程數值解新技術[M].北京:科學出版社,1992.
[5]祝家麟.橢圓邊值問題的邊界元分析[M].北京:科學出版社,1991.
[6]BREBBIA C A.The boundary element method for engineers[M].London:Pentech Press,1978.
[7]BREBBIA C A.Heat transfer,fluid flow and electrical applications[M].London:Computational Mechanics Publications,1988.

