基于場景概率潮流的電力系統(tǒng)無功優(yōu)化研究

熊 強，鄭永康

(1.西南交通大學電氣工程學院，四川 成都 610031；2.國網(wǎng)四川省電力公司電力科學研究院，四川 成都 610072)

基于場景概率潮流的電力系統(tǒng)無功優(yōu)化研究

熊 強1，鄭永康2

(1.西南交通大學電氣工程學院，四川 成都 610031；2.國網(wǎng)四川省電力公司電力科學研究院，四川 成都 610072)

多風電場出力的隨機性和互相關性特點對電力系統(tǒng)無功優(yōu)化調度有著不可忽視的影響。針對這一問題，提出一種基于場景概率潮流的電力系統(tǒng)無功優(yōu)化方法。該方法將風電出力場景化，結合概率潮流計算，以系統(tǒng)有功網(wǎng)損、發(fā)電機無功偏差和節(jié)點電壓偏差期望加權值最小作為無功優(yōu)化目標函數(shù)，利用粒子群算法求得各風電出力場景下的最優(yōu)無功控制策略。在含多風電場的IEEE 30節(jié)點系統(tǒng)中對所提方法進行測試，并與確定性的場景無功優(yōu)化方法相對比，驗證了所提方法的有效性。

概率潮流；場景；相關性；無功優(yōu)化

0 引 言

傳統(tǒng)的無功優(yōu)化研究大多是基于確定的系統(tǒng)模型，假定系統(tǒng)中的支路參數(shù)、負荷需求、發(fā)電機出力等保持不變。但在含多風電場的電力系統(tǒng)中風電出力的隨機性和相關性會對電力系統(tǒng)運行狀態(tài)會產(chǎn)生很大的影響[1]。如若不考慮這些影響，仍采用確定性的模型對系統(tǒng)進行無功優(yōu)化，所得到的控制策略往往不是最優(yōu)的，甚至可能起到惡化的效果。鑒于此，文獻[2]基于概率潮流計算方法，以網(wǎng)損期望值最小、電壓越限概率最小和負荷裕度最大為多目標，采用粒子群算法進行了無功優(yōu)化研究，但沒有考慮風電場之間的相關性對無功優(yōu)化的影響。文獻[3]考慮了隨機變量相關性，通過概率潮流計算方法對電力系統(tǒng)的電壓穩(wěn)定和無功優(yōu)化問題進行了研究，但由于文獻假設風速服從威布爾分布，故所得概率分析結果僅適用于系統(tǒng)長期或中長期評估[4]，實際參考價值有限。

針對這些問題，提出一種基于場景概率潮流的無功優(yōu)化方法，建立了多風電場出力的場景概率模型，結合蒙特卡洛模擬概率潮流計算方法[5]，利用改進的粒子群算法求得各場景下的最優(yōu)無功控制策略，為電力系統(tǒng)運行與規(guī)劃人員提供豐富的決策信息。

1 場景概率潮流計算

為了考慮多風電場出力的隨機性和相關性，將場景概率潮流計算引入到電力系統(tǒng)無功優(yōu)化問題中。首先，利用K均值聚類和Copula函數(shù)[6-7]建立了多風電場出力的場景概率模型，再結合蒙特卡洛模擬法在各場景中實現(xiàn)了概率潮流計算。具體實現(xiàn)過程如下。

1)風電出力場景化。利用K均值聚類在識別數(shù)據(jù)內(nèi)在結構上的優(yōu)點，將原始多風電場出力數(shù)據(jù)劃分為S類，并記錄每一類發(fā)生概率；

2)求取風電出力邊緣分布函數(shù)。采用非參數(shù)核密度估計[8]求得各場景中風電出力的邊緣分布函數(shù)；

3)構建多風電場出力場景概率模型。利用Copula理論建立各場景下風電出力的聯(lián)合概率分布函數(shù)；

4)場景概率潮流計算。對各場景下概率分布函數(shù)進行采樣，利用蒙特卡洛模擬實現(xiàn)概率潮流計算；

5)系統(tǒng)概率評估。對概率潮流計算結果進行統(tǒng)計分析，得到各狀態(tài)變量的統(tǒng)計特性及分布信息。

2 基于場景概率潮流的電力系統(tǒng)無功優(yōu)化

以場景概率潮流計算代替?zhèn)鹘y(tǒng)無功優(yōu)化中的確定性潮流計算，以系統(tǒng)有功網(wǎng)損、發(fā)電機無功偏差和節(jié)點電壓偏差期望加權值最小作為無功優(yōu)化目標函數(shù)，利用改進粒子群算法求得各風電出力場景下的最優(yōu)無功控制策略。

2.1 無功優(yōu)化數(shù)學模型

1) 目標函數(shù)

(1)

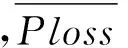
2) 等式約束條件

(2)

式(2)為系統(tǒng)潮流方程。

3) 不等式約束條件

(3)

式中，VGmin和VGmax分別為發(fā)電機端電壓上限值和下限值；KTmin和KTmax分別為可調變壓器分接頭的上限值和下限值；QCmin和QCmax分別為補償電容器投切組數(shù)的上下限值。

2.2 改進粒子群算法

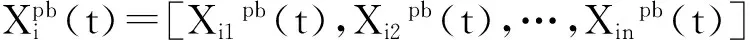
(4)

Xgb(t+1)=arg{minF(Xipb(t+1))}

(5)

粒子位置向量和速度向量每一維按式(6)、式(7)更新：

(6)

(7)式中，w(t)為慣性權重；c1和c2為權系數(shù)；r1(t)和r2(t)為0到1之間的隨機數(shù)；vmax為粒子最大速度；η為約束因子。

從式(6)可以看出w(t)能夠平衡PSO算法的全局搜索能力和局部尋優(yōu)能力，其值越大全局搜索能力較強；反之，局部搜索能力較強。在迭代初期，希望各粒子能夠具有較強全局探索能力；迭代后期，則希望粒子擁有良好的局部搜索能力。為此，采用線性遞減權重原則來動態(tài)調整慣性權重值[11]，見式(8)：

(8)

式中，wmax、wmin分別w最大值和最小值；Tmax為最大迭代次數(shù)。

2.3 算法流程

結合場景概率潮流和粒子群算法實現(xiàn)了考慮多風電場相關性的無功優(yōu)化研究，具體算法流程如下。

1) 輸入系統(tǒng)網(wǎng)絡參數(shù)，各風電場實測出力數(shù)據(jù)；

2) 利用K均值聚類將風電場出力數(shù)據(jù)劃分為L類；

3) 利用Copula函數(shù)建立各類中風電出力的聯(lián)合概率模型；

4) 對各場景概率模型進行采樣，得到各場景下的模擬風電出力數(shù)據(jù)，令T=1；

5) 選擇場景T樣本數(shù)據(jù)進行無功優(yōu)化；

6) 初始化種群，設置相關參數(shù)；

7) 利用概率潮流計算得到場景T中目標函數(shù)值；

8) 根據(jù)式(4)和式(5)更新粒子的最優(yōu)位置；

9) 判斷是否達到最大迭代次數(shù)：是，則進行下一步；否，則按式(6)和式(7)更新粒子的速度和位置；

10) 得到場景T的最優(yōu)無功控制策略，判斷T=L是否成立：是，則算法結束；否則令T=T+1，轉入步驟5)循環(huán)迭代。

3 算例分析

在含多風電場的IEEE30節(jié)點系統(tǒng)中對所提方法進行仿真測試，系統(tǒng)結構如圖(1)所示。算例將負荷節(jié)點分為兩個區(qū)域：1-15和16-30，區(qū)域內(nèi)相關系數(shù)為0.9，區(qū)域間相關系數(shù)為0.5，并假設負荷隨機變量服從正態(tài)分布。在節(jié)點6和9接入兩個風電場，其出力數(shù)據(jù)取自兩個相鄰風電場的實測出力值。該系統(tǒng)中控制變量如表1所示。

算例中PSO算法的參數(shù)設置如下：學習因子取經(jīng)典值c1=c2=2；慣性權重w(t)最大最小值分別取為0.95和0.4；約束因子η=0.729；種群數(shù)取為30，最大迭代次數(shù)為100，粒子維數(shù)為13；目標函數(shù)中懲罰因子λQ=1，λV=100。在概率潮流計算中采樣規(guī)模取為500。

表2為基于場景概率潮流的電力系統(tǒng)無功最優(yōu)控制策略，圖2為各場景無功優(yōu)化過程中PS0算法收斂曲線。

決策人員可根據(jù)表2根據(jù)風電出力所處的場景進行相應的調度控制。此外，從加權目標函數(shù)值可以看出，隨著風電出力的增加，優(yōu)化后的系統(tǒng)運行狀態(tài)更優(yōu)。圖2可以看出，各場景無功優(yōu)化在70代左右收斂到最優(yōu)值。

表1 IEEE 30節(jié)點系統(tǒng)控制變量信息表

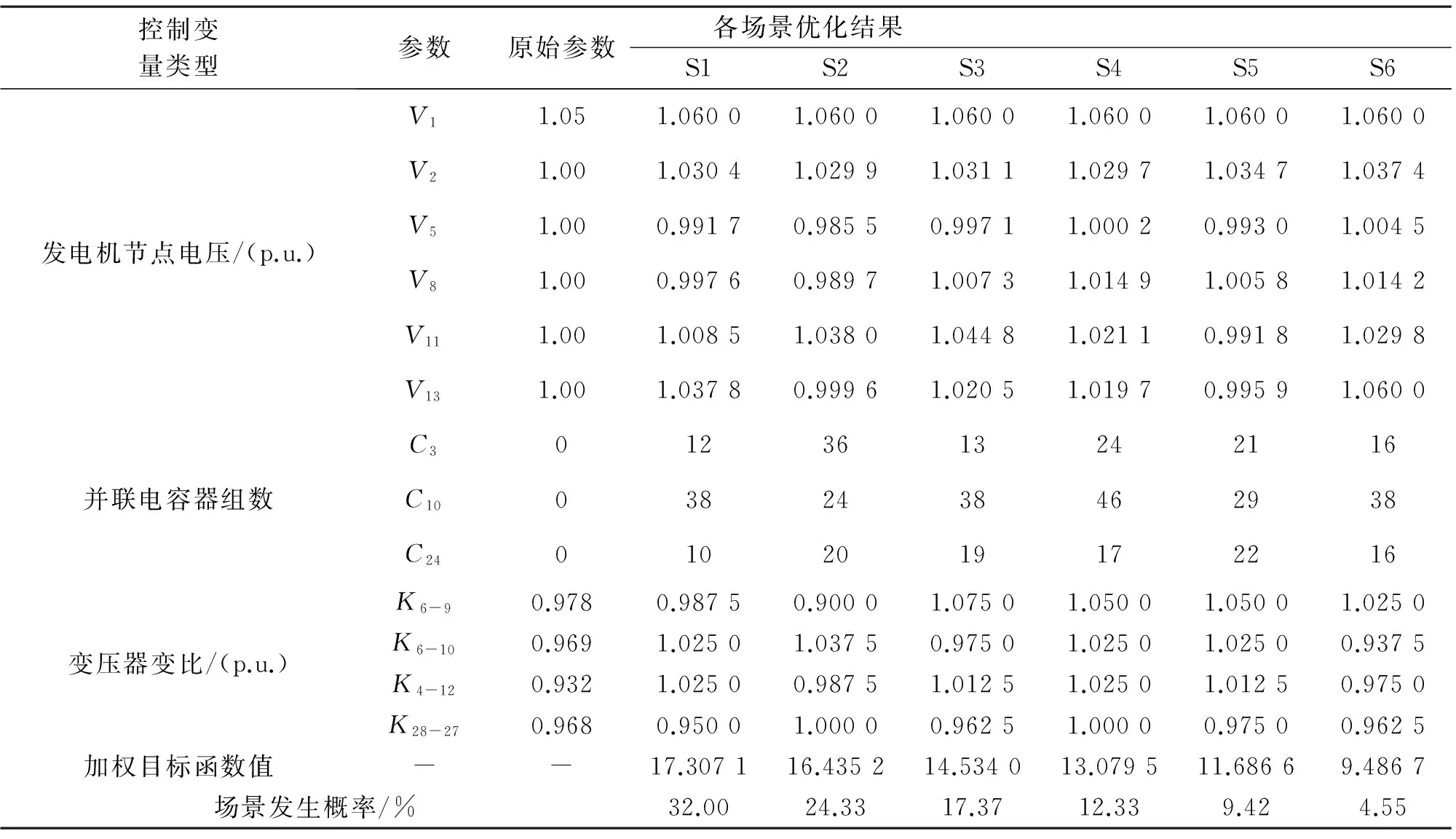
表2 場景概率模型最優(yōu)無功控制策略

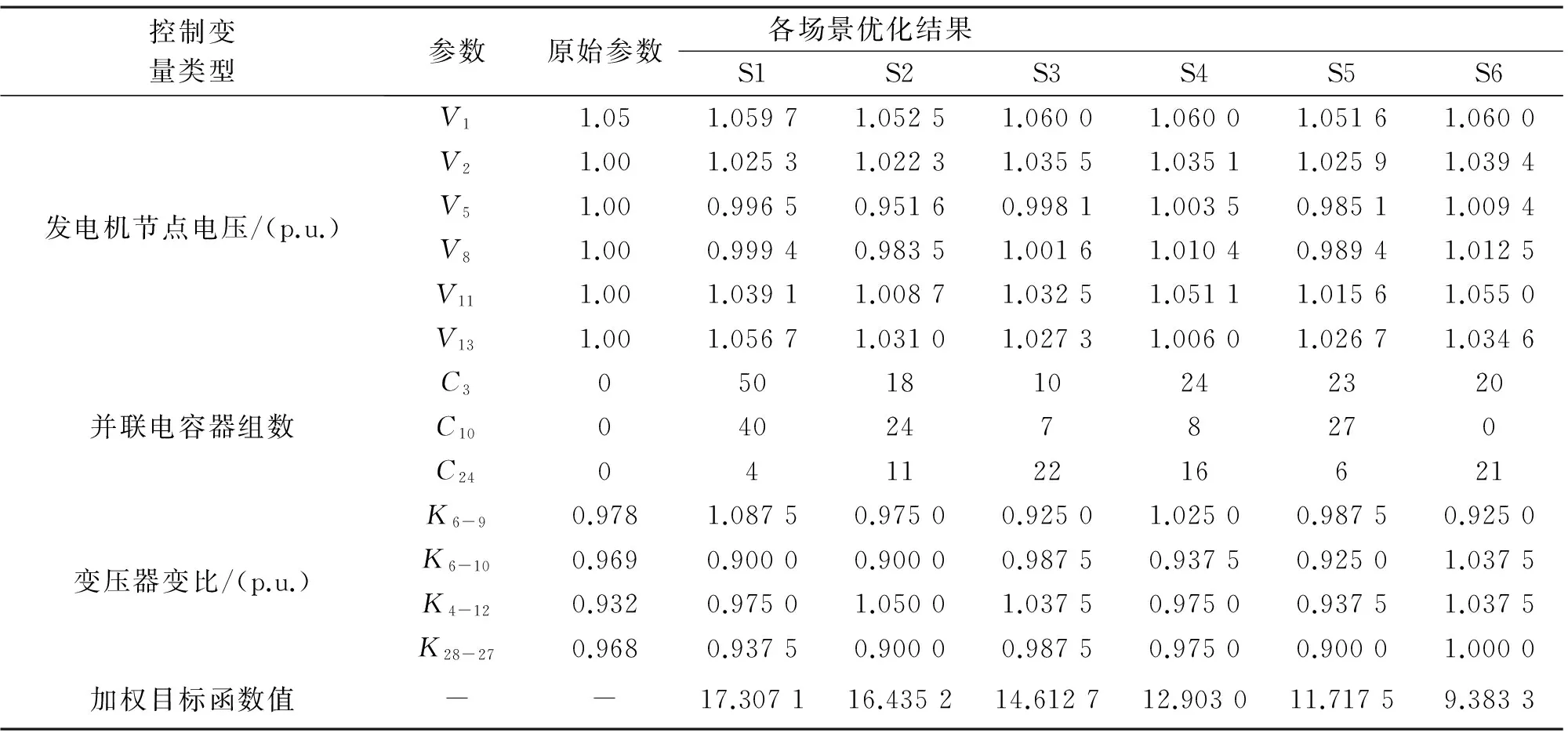
表3 確定模型最優(yōu)無功控制策略

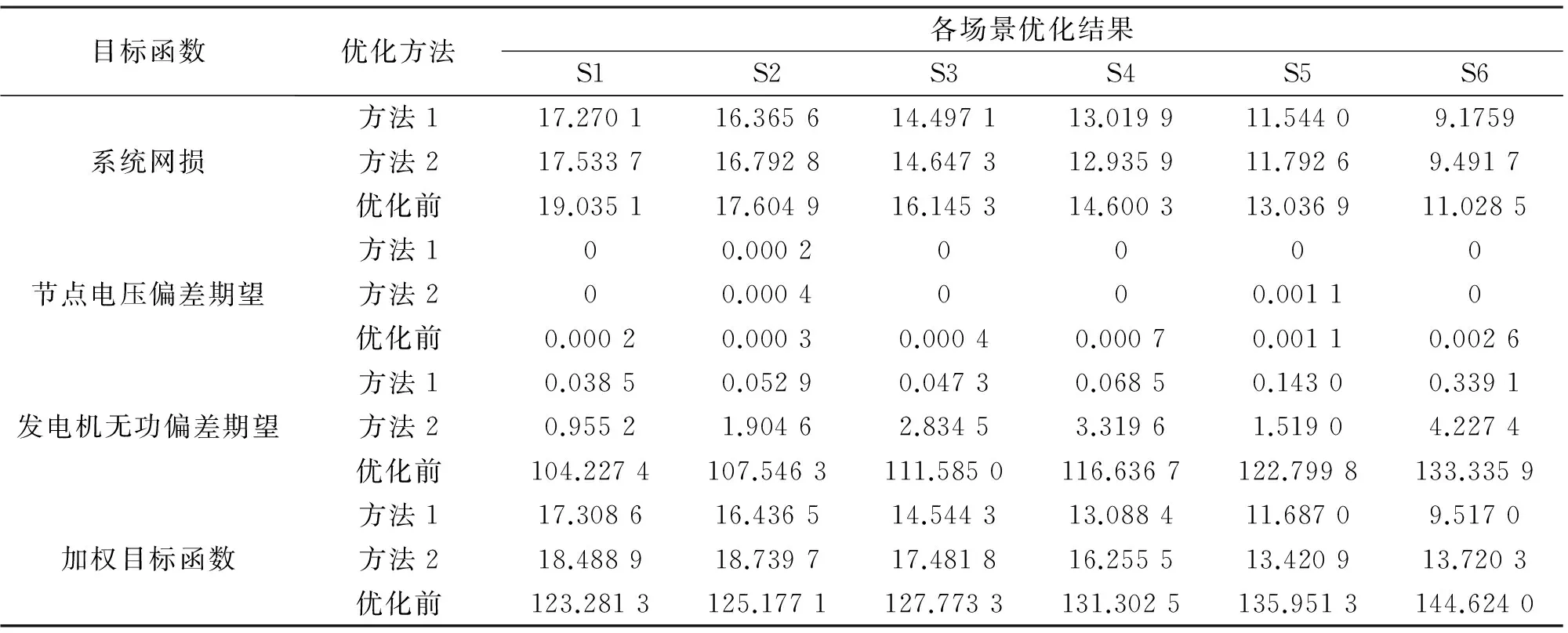
表4 不同優(yōu)化方法各場景結果比較

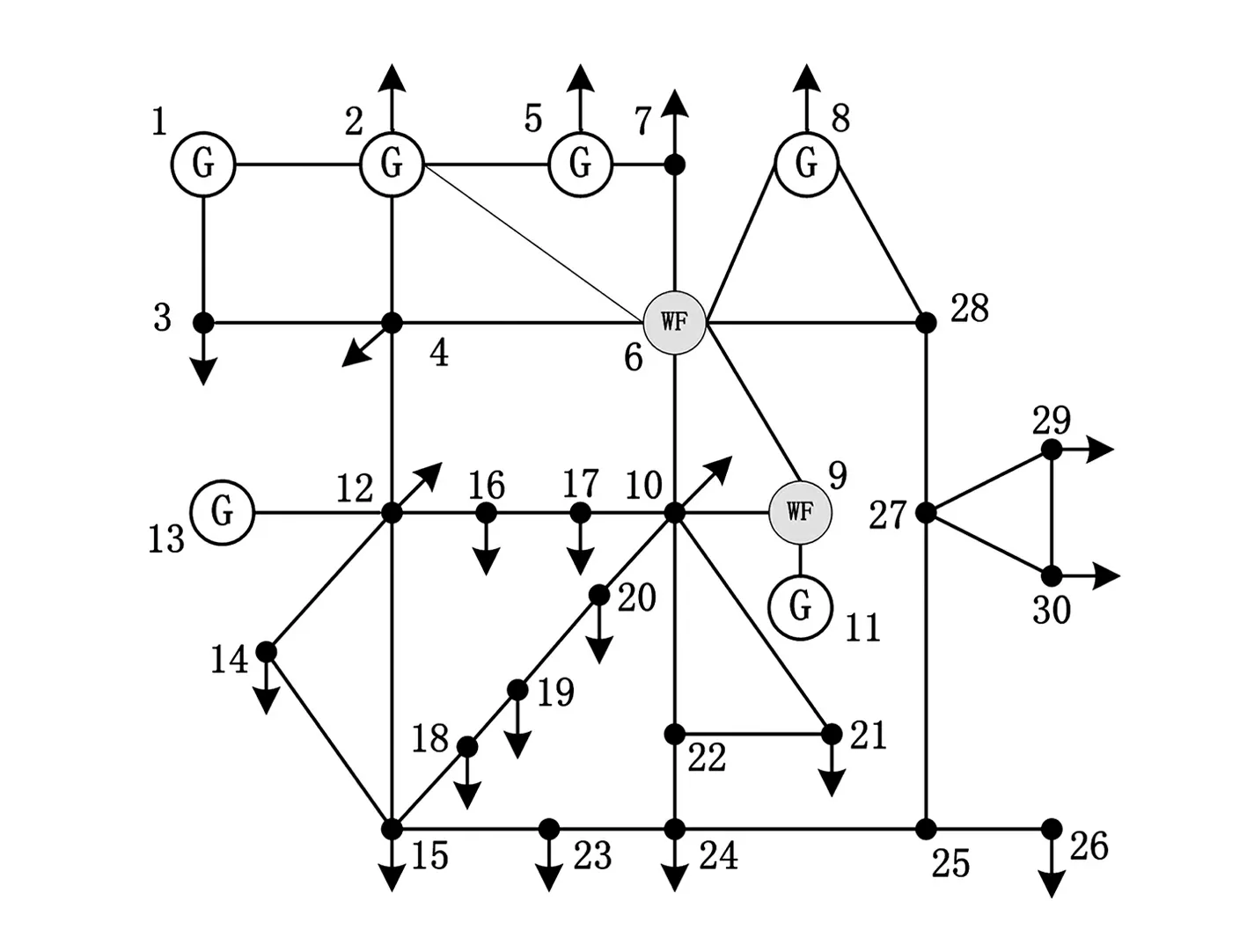
圖1 含兩個風電場的IEEE 30節(jié)點系統(tǒng)

為了驗證所提方法優(yōu)于傳統(tǒng)確定性無功優(yōu)化方法，將兩種方法進行了對比分析：其中方法1為所提方法；方法2為傳統(tǒng)的確定性場景無功優(yōu)化方法，即不考慮系統(tǒng)中存在的不確定因素，將各場景中風電出力的平均值作為實際出力，代入無功優(yōu)化模型，以確定性潮流計算所得適應值作為目標函數(shù)，得到各場景下的最優(yōu)無功控制策略。

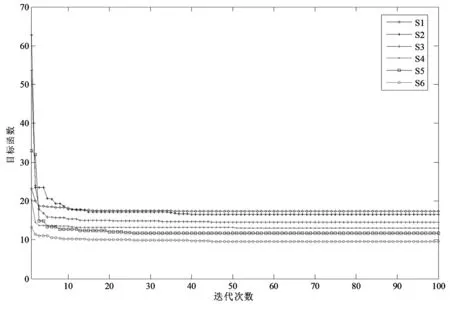
圖2 各場景PSO收斂曲線

由于在實際電網(wǎng)運行過程中，風電出力和負荷不可能固定不變，故將方法2所得到的最優(yōu)控制策略代入方法1考慮隨機因素的目標函數(shù)中，將所得各場景下的適應值與方法1的結果相對比。

表3為方法2各場景最優(yōu)無功控制策略；表4為兩種方法對比結果。

對比表3和表4可以看出：在最優(yōu)控制策略下方法1和方法2在各場景中的加權目標函數(shù)值相差都很小，個別場景方法2甚至優(yōu)于方法1。從表4可以看出，在考慮風電出力隨機變化時，雖然兩種方法都能較大程度上實現(xiàn)對系統(tǒng)的優(yōu)化，但在方法1的最優(yōu)控制策略下，系統(tǒng)的各項指標明顯優(yōu)于方法2，說明方法1能夠考慮系統(tǒng)中存在的隨機變量，得到更可靠的無功優(yōu)化策略。

4 總 結

將場景概率潮流計算方法應用到電力系統(tǒng)無功優(yōu)化研究中。充分考慮了系統(tǒng)中負荷、風電出力的隨機性和相關性，從概率的角度得到了各場景下的最優(yōu)無功控制策略。與傳統(tǒng)的確定性無功優(yōu)化方法相比，所提方法在含不確定性因素的系統(tǒng)中表現(xiàn)更優(yōu)，所得到的無功配置方案能夠適應隨機因素的變化，為運行與規(guī)劃人員提供更可靠、更全面、更經(jīng)濟的控制策略。

[1] 潘雄, 周明, 孔曉民, 等. 風速相關性對最優(yōu)潮流的影響[J]. 電力系統(tǒng)自動化, 2013(6):37-41.

[2] 柳杰, 劉志剛, 孫婉璐, 等. 含風電場電力系統(tǒng)電壓穩(wěn)定性概率評估及其在無功優(yōu)化中的應用[J]. 電網(wǎng)技術, 2012(11):134-139.

[3] 李鴻鑫. 考慮不確定性因素的電力系統(tǒng)電壓穩(wěn)定與無功優(yōu)化問題研究[D].武漢： 華中科技大學, 2013.

[4] 朱星陽, 劉文霞, 張建華, 等. 電力系統(tǒng)隨機潮流及其安全評估應用研究綜述[J]. 電工技術學報, 2013(10):257-270.

[5] 陳雁, 文勁宇, 程時杰. 考慮輸入變量相關性的概率潮流計算方法[J]. 中國電機工程學報, 2011(22):80-87.

[6]NelsenRB.AnIntroductiontoCopulas[M].SpringerScience&BusinessMedia, 2007.

[7] 黎靜華, 韋化. 基于內(nèi)點法的機組組合模型[J]. 電網(wǎng)技術, 2007(24):28-34.

[8] 秦志龍. 計及相關性的含風電場和光伏電站電力系統(tǒng)可靠性評估[D]. 重慶：重慶大學, 2013.

[9] 梁艷春. 群智能優(yōu)化算法理論與應用[M].北京：科學出版社, 2009.

[10] 陳前宇, 陳維榮, 戴朝華, 等. 基于改進PSO算法的電力系統(tǒng)無功優(yōu)化[J]. 電力系統(tǒng)及其自動化學報, 2014,26(2):8-13.

[11]ShiY,EberhartR.AModifiedParticleSwarmOptimizer[C].IEEE,WorldCongressonComputationalIntelligence，1998.

The randomness and cross-correlation of wind farms output have a negligible impact on reactive power optimization scheduling of power system．Aiming at this problem, a reactive power optimization method based on scenario probabilistic load flow is proposed. The wind farm output is scenarized in this method. Combining with the probabilistic load flow, it takes the minimum weighted value of system network loss expectation, generator reactive power and node voltage deviation expectation as the target function and uses the particle swarm optimization to get the optimal reactive power control strategy in each scene. The proposed method is tested in IEEE 30 node system including wind farms and compared with the deterministic scenarios optimization method. The simulation results demonstrate the effectiveness of the proposed method.

probabilistic load flow; scenario; correlation; reactive power optimization

TM74

A

1003-6954(2015)03-0068-05

2015-04-07)

熊 強(1989)，碩士研究生，研究方向為電力系統(tǒng)及其自動化；

鄭永康(1977)，博士，高級工程師，主要研究方向為繼電保護。