信號降噪中小波基與閾值的選取研究
□ 羅 淼 □ 姚運萍
蘭州理工大學機電工程學院 蘭州 730050
在信號的生成與傳輸過程中,經常由于受到噪聲的影響使得質量變差,因此有針對性地從測量數據中獲得有效信息,對信號進行降噪是許多分析過程的重要一步[1]。傳統的降噪是將被噪聲干擾的信號通過濾波器將無用噪聲成分去除,但對脈沖信號、白噪聲、非平穩過程信號等,具有一定的局限性。近些年來,由于小波理論的不斷發展,使其在信號降噪方面有獨特的優越性,因而被廣泛應用。小波分析的一般過程是先把信號分解為小波系數,然后對分解出來的系數根據問題的要求做一些處理,再用小波重建方法恢復信號[2]。
1 小波降噪方法
1981年,法國地理物理學家Morlet在分析地質探測數據時,基于群論首先提出了小波分析這一概念,隨后他和法國物理學家Grossmann開始一起共同研究小波理論,發展了連續小波變換的理論體系。1985年,法國數學家Meyer、物理學家Grossmann及比利時數學家Daubechies等共同研究,得到了一組離散小波基。1988年,Daubechies提出了具有緊支集的正交基,即Daubechies基。美國研究者Weaver等最早將小波變換用于圖像降噪[3],Weaver等所用的算法是一種簡單的閾值降噪法。所謂閾值濾波就是把小波系數的幅值同一個閾值進行比較,若小波系數的幅值比這個閾值小,則把小波系數置為0;若小波系數的幅值比這個閾值大,則把小波系數保留或進行修改后保留。隨后美國數學家Donoho等對小波閾值濾波算法作了系統闡述,成為小波濾波方法的一個具有里程碑意義的研究成果。
1.1 小波變換原理
小波函數是由一個小波“母函數”經過伸縮和平移而得到的一簇函數。若φ(t)為小波母函數,則由其派生出來的小波函數為:
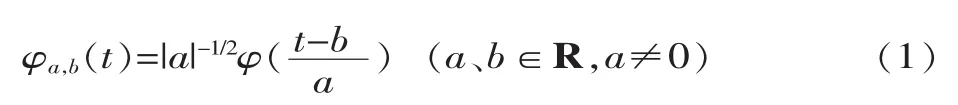
式中:a是伸縮的尺度;b是平移的距離。
并非任何函數都可以成為小波母函數,小波母函數必須滿足一定的條件。令:

則 φ(t)為小波母函數的必要條件為 Cφ<+∞,Cφ<+∞又叫作可容許(admissible)條件。可容許條件說明ω=0 時,一定為 0,即:
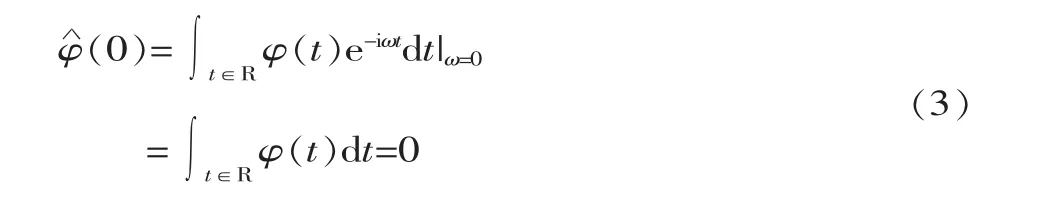
這說明函數φ(t)必須要有一定的波動性。函數f(t)的連續小波變換可表示為:

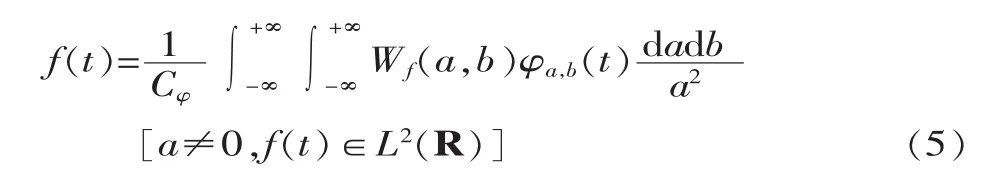
可以看出,小波變換是一種可以保持信息內容的可逆變換,信息保存于小波變換系數中,經過反變換后即可恢復。
在實際應用中,需要將小波離散化才有意義[4]。離散小波就是將連續小波的尺度參數和平移參數離散化,若令 a>1,b>0,則定義離散小波為:

小波變換是對Fourier變換的繼承和發展,使變換結果既有一定的頻率分辨率,又有一定的時間分辨率。小波變換的一個重要特性是其具有“變焦”的特性,對非平穩信號具有很強的適應性,因此很適合對信號進行降噪處理。
1.2 降噪基本原理
假設信號 f(n)被噪聲污染后為 s(n),則可以建立噪聲模型:

式中:e(n)為噪聲;σ 為噪聲強度。
在簡單情況下可假設e(n)為高斯白噪聲,且σ=1。利用小波變換去噪就是要通過抑制噪聲e(n),從而盡可能恢復原信號 f(n)。
從統計學的觀點看,這個模型是一個隨時間推移的回歸模型,也可以看作是在正交基上對函數f(n)的無參估計[5]。
小波去噪的整個過程可以分以下三步進行。
第一步,利用離散小波變換(DWT)進行信號分解,選擇適當的小波基以及分解層數。
第二步,確定小波域的閾值,對小波系數進行閾值截斷。
第三步,利用截斷后的系數進行小波重構。
1.3 閾值的處理
小波閾值是根據噪聲模型和原信號的信噪比來確定的,在模型中,這個量由標準方差σn來表示。在得到夾雜白噪聲的信號后,可以由噪聲強度σ來確定閾值。最常用的確定方法為Donoho提出的統一閾值,閾值Thr的選擇滿足:

式中:N為信號的長度。
這種方法在實際應用中效果不是很好,比較常用的閾值選取方法有以下幾種[6]。
(1)基于無偏似然估計的軟閾值估計(Rigrsure),最佳閾值通過選擇風險最小的閾值達到。
(2) 長度對數閾值 (Sqtwolog), 其閾值等于
(3)啟發式閾值(Heursure),這種方法是長度對數閾值和軟閾值估計的綜合,利用啟發函數在上述兩種閾值估計方法中選取一個。
(4)最小極大方差閾值(Minimaxi),這種方法利用求得的回歸函數與原信號的方差在最壞的情況時的最小值得到閾值,使選取的閾值產生最小均方誤差的極值。
筆者所用的閾值選擇方法先是利用Birge-Massart算法求得小波變換閾值,再根據合適的閾值確定閾值選取范圍,最終取得最優閾值。Birge-Massart是針對給定的分解層數j,保留j+1以及更高層的系數,然后對第 i層(1≤i≤j),保留絕對值最大的 ni個系數:

式中:M和α是經驗系數,在缺省情況下為第一層分解后的系數長度,在降噪時α=3。
選擇閾值函數對小波系數進行閾值處理,即對其系數進行截斷。常用的閾值函數主要有硬閾值函數和軟閾值函數[7],如圖1、圖2所示,圖中橫坐標表示信號的原始小波系數,縱坐標表示閾值化后的小波系數,T為估計閾值。
硬閾值函數:

軟閾值函數:

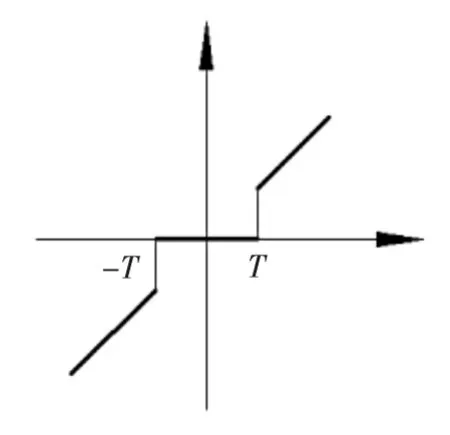
▲圖1 硬閾值函數
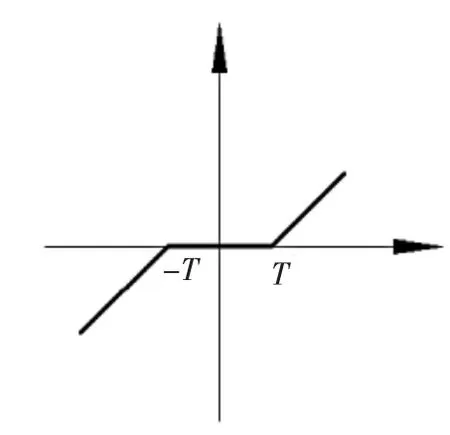
▲圖2 軟閾值函數
硬閾值方法可以較好地保留信號邊緣等局部特征,但濾波后信號容易突變,產生較大的振蕩(稱為吉布斯現象)[3];軟閾值處理后信號較為平滑,但易造成模糊等失真現象。
2 小波降噪的MATLAB仿真
測試信號采用Doppler信號。小波基的一般選取原則有正交性、緊支性、對稱性、平滑性、消失矩陣階數,由于一般小波基的選擇是根據與原信號相似原理,所分析的信號和所選小波基需存在一定的相似性。sym小波的構造類似于db小波族,兩者的差別在于sym小波有更好的對稱性[8]。故對Doppler信號進行降噪處理,采用 symN小波基。 初選 symN(N=1,2,…,15)為預選小波基系列,給Doppler信號加入高斯白噪聲SNR為16 dB。
對于降噪效果的評估,采用最小化平均平方誤差MSE(Mean Squared Error)及信噪比 SNR(Signal to Noise Ratio)來進行評價:

式中:xi為原圖像第i個像素;為降噪后圖像的第i個像素。

對加有噪聲的Doppler信號按照硬閾值函數,分解層數初選為四層進行降噪處理。信號的信噪比越高,最小化平均平方誤差越小,則表明降噪效果越好。
各小波基對信號降噪后的效果見表1,從表中可以看出,不同的小波基降噪效果不同,對于測試信號而言,sym10、sym13、sym15降噪效果較好。 對于不同的信號,小波基的選取決定降噪的好壞。經過多次仿真發現,sym10小波基對于Doppler信號的降噪效果較好,最終選取sym10小波基作為降噪過程采用的小波基。使用Birge-Massart算法獲取小波變換的最佳閾值在0.57左右,為確定最優閾值,可將閾值搜索區間定為0.55至0.65,各閾值去噪效果對比如圖3所示。最終經過多次仿真,確定最優閾值為0.6。確定小波基和閾值后,進一步確定最優分解層數。實驗取分解層數為1~10層,不同分解層數的降噪效果見表2。
從表2的實驗結果中可以看出,分解層數小于4時,降噪后的信號有明顯的突變、尖峰情況。分解層數為3時的降噪效果如圖4所示。當層數逐漸增加,效果逐漸平滑。分解層數為5、6、7層時,降噪效果較好,信號比較平滑,最后經過綜合評定,選定最終的分解層數為6層。降噪后的信號如圖5所示,采用上文提出的4種閾值選取規則對原信號進行降噪處理,各種方法得到降噪效果見表3。
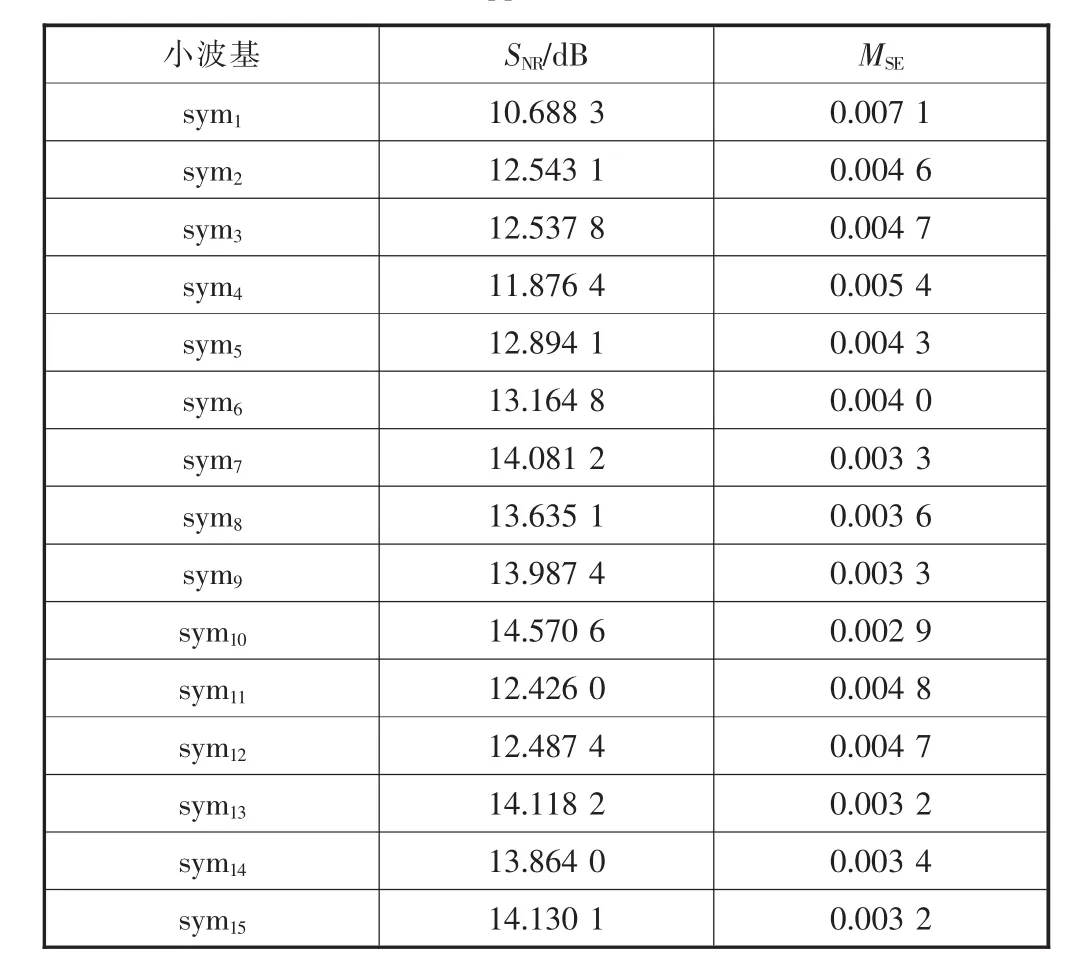
表1 各小波基對Doppler信號降噪后的效果評價
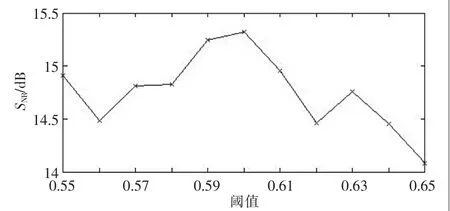
▲圖3 不同閾值的去噪效果曲線圖
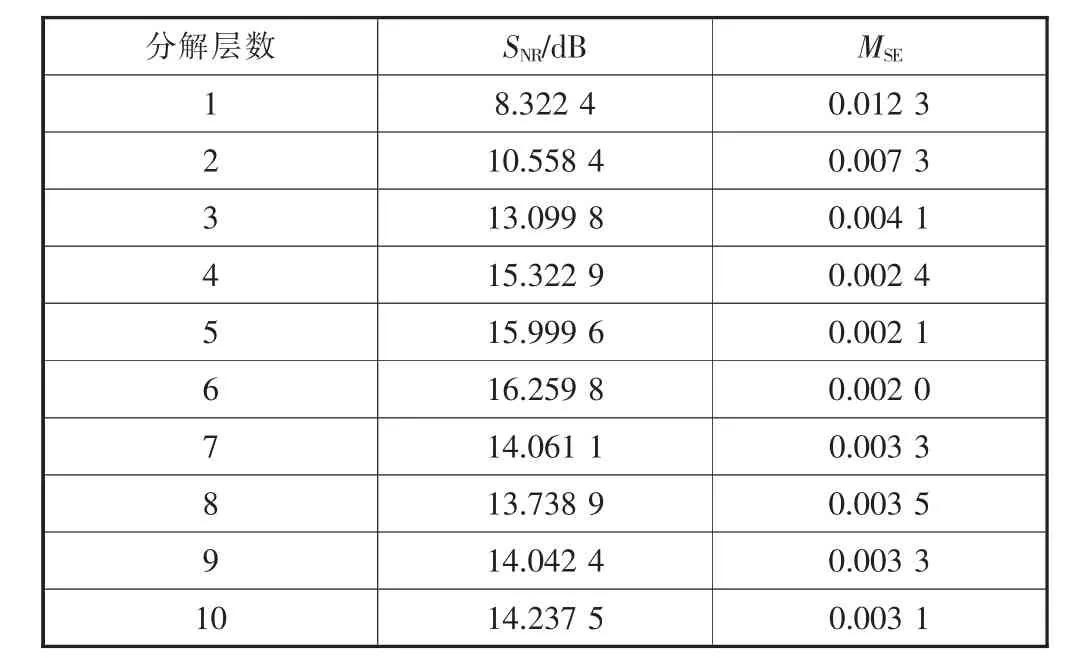
表2 不同分解層數的降噪效果

表3 不同閾值選取規則的降噪效果
從表3中可以看出,筆者所采用的小波基及閾值選取方法的降噪效果優于其它方法。
3 結論
通過分析可知,根據相似性原理,對Doppler信號的降噪處理采用sym小波基,其中小波的分解層數對信號的去噪影響較為顯著,分解層數較小時,經過降噪處理的信號有突變和尖峰現象,隨著分解層數的增加,信號逐漸趨于平滑,得到較好的降噪效果。
對于小波基的選擇是一項艱難而又復雜的工作,筆者僅通過對Doppler信號降噪過程的小波基與閾值選取做了有限的分析,對于實際復雜信號降噪中的小波基與閾值選取需根據不同情況進行。

▲圖4 分解層數為3時的降噪效果
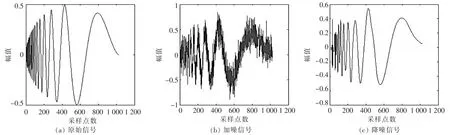
▲圖5 分解層數為6時的降噪效果
[1]倪林.小波變換與圖像處理[M].合肥:中國科學技術大學出版社,2010.
[2]李保霖,趙建川,藺文彬.小波分析在信號降噪中的應用[J].電子設計工程,2013,21(9):39-42.
[3]姜三平.基于小波變換的圖像降噪[M].北京:國防工業出版社,2009.
[4]高成,董長虹,郭磊,等.Matlab圖像處理與應用[M].北京:國防工業出版社,2007.
[5]吳偉,蔡培升.基于MATLAB的小波去噪仿真[J].信息與電子工程,2008,6(3):220-222,229.
[6]許文博,武曉春,邢建平.一種新的小波閾值去噪方法[J].蘭州交通大學學報,2012,31(3):120-124.
[7]周偉.基于MATLAB的小波分析應用[M].西安:西安電子科技大學出版社,2010.
[8]董長虹,高志,余嘯海.Matlab小波分析工具箱原理與應用[M].北京:國防工業出版社,2004.

