利用HSSIM和殘差比閾值的3維激光掃描圖像去噪

崔 治，鄧曙光，肖衛初

(湖南城市學院通信與電子工程學院，益陽413000)

引 言

3維激光掃描是以獲取被測物體輪廓數據為目的的一種成像技術，與一般CCD成像相比，利用3維激光掃描獲取的圖像紋理豐富、分辨率高、具有更好的強度和范圍信息，在目標探測、遙感和醫學等方面潛力巨大［1］。然而在實際工作中，3維激光掃描圖像不可避免地受到環境噪聲、儀器噪聲和信號傳輸過程中的隨機噪聲等的影響引起圖像質量下降，進而影響到信息的正確表達。因此，對獲取的掃描圖像進行噪聲分析、評估和去噪一直是相關領域的研究熱點。

目前，針對激光掃描圖像的去噪，常用的方法是基于變換域的處理方法，這種方法認為圖像中噪聲的能量主要集中在高頻部分，而內容等細節特征分布在低頻部分，通過尋找圖像中頻譜分布的規律，從頻域上將圖像的內容等細節特征和噪聲分開，可以達到去噪的目的［2］。但是，大量的實驗表明，在現實條件下采集到的圖像，其頻譜中的高頻部分也含有與內容相關的細節，在低頻部分也能檢測到噪聲的存在，當按照上述變換域方法進行去噪時，圖像的一部分內容細節會隨著噪聲的濾除而丟失，而位于低頻部分的噪聲卻無法被很好地去除［3］。

稀疏表示理論作為一種新興的信號分析與處理理論，近年來受到廣泛的關注。該方法的基本思想是采用過完備字典中的冗余基系統來取代變換域方法中的正交基系統，對信號的稀疏分解就是從過完備字典中選擇具有最佳組合的若干個原子來表示信號，通過判斷數據在字典上是否具有稀疏表示來區分有用信息與噪聲，實現去噪的目的［4］。參考文獻［5］中提出一種基于核模糊聚類的去噪方法，該方法通過將圖像分成大小相同的若干塊并對相似的圖像塊進行C均值聚類，使同類圖像塊能共享相同的稀疏去噪模型從而實現去噪的目的。參考文獻［6］利用K-means和主成分分析構造了一種貝葉斯去噪模型，利用正則化條件計算原始圖像與學習字典的差，以達到優化噪聲的效果。文獻［7］提出基于自適應聚類的去噪算法，采用K-means算法訓練過完備字典，利用訓練中的每一步迭代自適應的更新字典原子，最后利用正交匹配追蹤算法(orthogonal matching pursuit，OMP)對圖像進行稀疏表示以實現圖像去噪。這些研究極大地豐富了稀疏表示應用，取得了較好的效果。

但是，現有基于稀疏表示的圖像去噪方法大多以去噪前后兩幅圖像的重構誤差作為保真項，以硬閾值作為迭代的終止條件，將其應用于3維激光圖像去噪時，在去噪的同時有可能丟失圖像的結構特征等重要信息。鑒于此，本文中將直方圖結構相似度(histogram structural similarity，HSSIM)和信號分解殘差比概念引入稀疏表示應用，提出一種基于融合直方圖結構相似度和殘差比閾值的改進算法，并對不同噪聲水準下不同圖像的峰值信噪比(peak signal-to-noise ratio，PSNR)和HSSIM數據及視覺主觀效果進行對比，以此評估算法的性能。

1 3維激光掃描圖像稀疏去噪原理

1.1 去噪模型

一般情況下，一幅位移不變的3維激光掃描圖像可用下面的方程表示:

式中，矩陣X，Y和Z分別表示觀測圖像、原始清晰圖像(理想圖像)和降質過程中引入的噪聲。對圖像進行去噪的目的就是在上面模型中去除噪聲或者降低噪聲Z帶來的影響，使觀測圖像X與原始清晰圖像Y之間的差別最小。

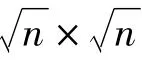
式中，a∈Rm為稀疏表示系數;為a的非零項的個數，表示a的稀疏度;D為字典;ε為微小正常數。

假定圖像X是通過加入標準差為σ的高斯白噪聲而降質得到，則對X進行去噪的結果為下面方程的解［9］:

式中，T為硬閾值，其它參量的釋義與上面一致。去噪后的圖像可表示為Y=D^a。

將(3)式中的約束條件轉化為懲罰項，根據正則化優化的思想可以將(3)式改寫為［10］:

式中，u是正則化參量。求解上式是一個 NP-hard問題，當u取合適值時，(3)式和(4)式可以相互等價的轉換。

1.2 對去噪模型的求解

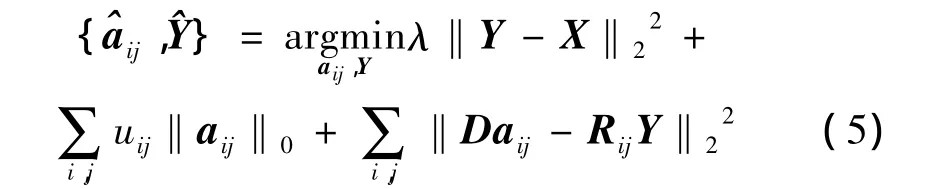
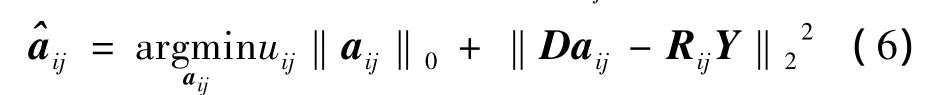
2 基于HSSIM和殘差比的去噪算法

2.1 HSSIM和殘差比的概念

首先定義兩組指標。

(1)HSSIM

直方圖結構相似度(HSSIM)是在對人眼視覺系統的特性進行分析時提出的一種新的圖像質量評價指標。若用x，y代表觀測圖像和原始圖像，用H(x，y)表示求兩者的直方圖結構相似度，其計算式如下［12］:

式中，μx和μy是兩幅圖像的均值;σx和σy是兩幅圖像的方差;c1，c2，c3是和圖像中像素值取值范圍有關的極小正常數;sx和sy是兩幅圖像的模糊度。

HSSIM是一個大于0而小于1的數，越接近1表明兩幅圖像在結構上的相似度越高，反之則表明相似度越低。

(2)殘差比

對(1)式進行如下修改:

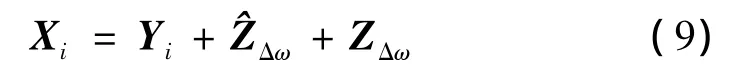
式中，Xi表示觀測圖像矩陣的列向量，Yi表示清晰圖像轉化后的列向量，Δω 表示 Yi的帶寬，和 ZΔω分別表示位于頻帶Δω之內和之外的噪聲。參考文獻［13］中認為，ZΔω與字典中的所有原子均正交，因此對圖像進行第m步和第m+1步稀疏分解的殘差可以由下式表示:

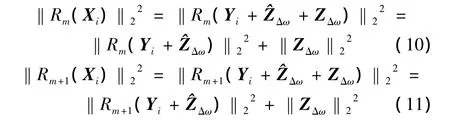
式中，Rk(·)表示第k步分解的殘差。

則殘差比為:

式中，β為規格化系數:

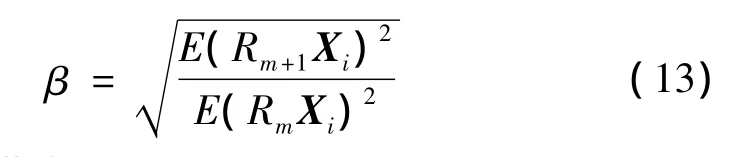
式中，E表示求期望值。

2.2 本文中算法設計

綜合上述分析，本文中提出一種改進的3維激光掃描圖像去噪模型:

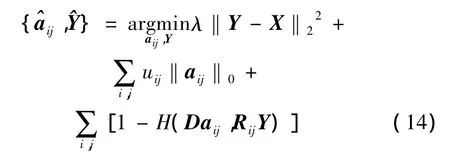
式中，等號右邊的第1項和第2項為約束項，第3項是相似因子，用來取代重構誤差作為新的保真項進行迭代計算，H(·)表示求取直方圖結構相似度。

對本文中模型進行求解，先假定D為已知過完備字典，代入初始條件為Y=X，可得每個圖像塊的最優解:

令1－H(Daij，RijY)＜η(η 為殘差比閾值)，通過求取偏導數求解(16)式得到去噪圖像的求解結果:

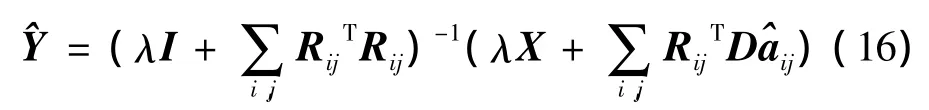
式中，I為單位矩陣。

由此可以歸納本文中算法的步驟如下。

(1)采用過完備的離散余弦變換(discrete cosine transform，DCT)字典為初始化字典D，代入初始條件Y=X。

(2)根據(9)式，將直方圖結構相似度加入到正交匹配追蹤算法中，對每個圖像塊進行稀疏編碼。在此過程中，將迭代終止條件修改為1－H(Daij，RijY)＜η。綜合考慮去噪效果和算法效率，經多次對比后確定殘差比閾值取值為0.005。

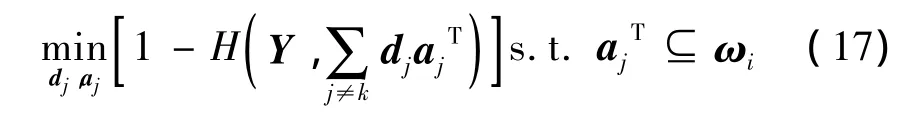
上面方程可以通過對Ek進行奇異值分解并求取1秩逼近來求解:

式中，U，V是m×m和n×n的酉矩陣，Δ是m×n的半正定對角陣。更新后的字典原子的第1列就是U的第1列，而稀疏系數矩陣更新后的第1列是Δ(1，1)和VT相乘后的第1列。

重復步驟(3)，直到全部迭代結束，得到稀疏字典。

3 實驗結果與分析

為了測試本文中算法的性能，選取3維激光掃描圖像測試庫中的島嶼、丘陵和雕刻版掃描圖進行實驗，如圖1a、圖2a和圖3a所示。3幅圖像的大小均為256像素×256像素，位深均為8，由圖可見，它們具有豐富的細節特征。

Fig.1 Laser-1 image with the denoised results of four methods

Fig.2 Laser-2 image with the denoised results of four methods

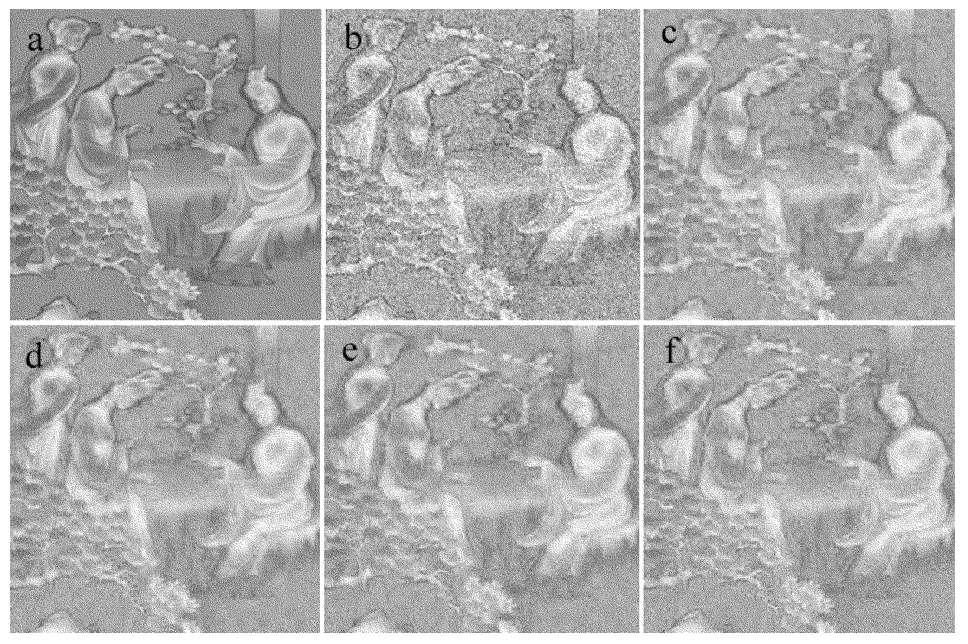
Fig.3 Laser-3 image with the denoised results of four methods

給3幅圖像分別添加方差σ為10，15，20的高斯白噪聲，再分別采用db2小波硬閾值去噪法、多尺度曲波變換(curvelet)、DCT和本文中算法進行對比性去噪實驗。實驗所用軟件為MATLAB 7.0，從評價的客觀性方面考慮，除了從視覺感受上來評價去噪圖像，還采用PSNR和HSSIM作為客觀指標來衡量不同算法的去噪效果。這兩項數據越大，表明算法的去噪效果越好，圖像特征保留的程度越高。對圖1a、圖2a和圖3a這3幅圖像采用上述4種方法去噪后的PSNR和HSSIM數據如表1和表2所示。從表中可以看到，對于相同的圖像，在添加的噪聲方差相同的情況下，采用本文中算法獲得的PSNR和HSSIM數據要優于其它3種方法。如對laser-2(丘陵)圖像加入σ=10的白噪聲后，采用本文中算法去噪后的PSNR值為36.17dB，相比db2小波變換、curvelet變換和離散余弦變換分別高出 6.24dB，0.35dB 和0.06dB;采用本文中算法獲得的HSSIM值為0.9764，相比db2小波變換、curvelet變換和離散余弦變換則提高了 0.1113，0.0296和0.0162。對不同的圖像加入不同水平的噪聲，采用本文中算法的結果依然優于其它3種方法。分析原因如下:(1)多尺度變換存在選擇最優基函數和最佳分解層數的問題，在基函數和分解尺度未進行最優匹配的情況下，處理結果不盡如人意;(2)多尺度變換在分解與重構的過程中有可能將圖像邊緣等結構特征當成高頻噪聲去除，導致去噪結果不理想。而稀疏表示將可用信息與噪聲進行確定性的區分，全面地從帶噪圖像中提取有用信息，實現對圖像的高質量重構，因此基于稀疏表示的方法處理效果較好。同時，本文中算法利用結構相似性因子作為保真項，利用殘差比閾值作為迭代終止條件，在保留圖像特征信息方面更具優勢，更符合人眼視覺系統的特性，去噪效果更好。

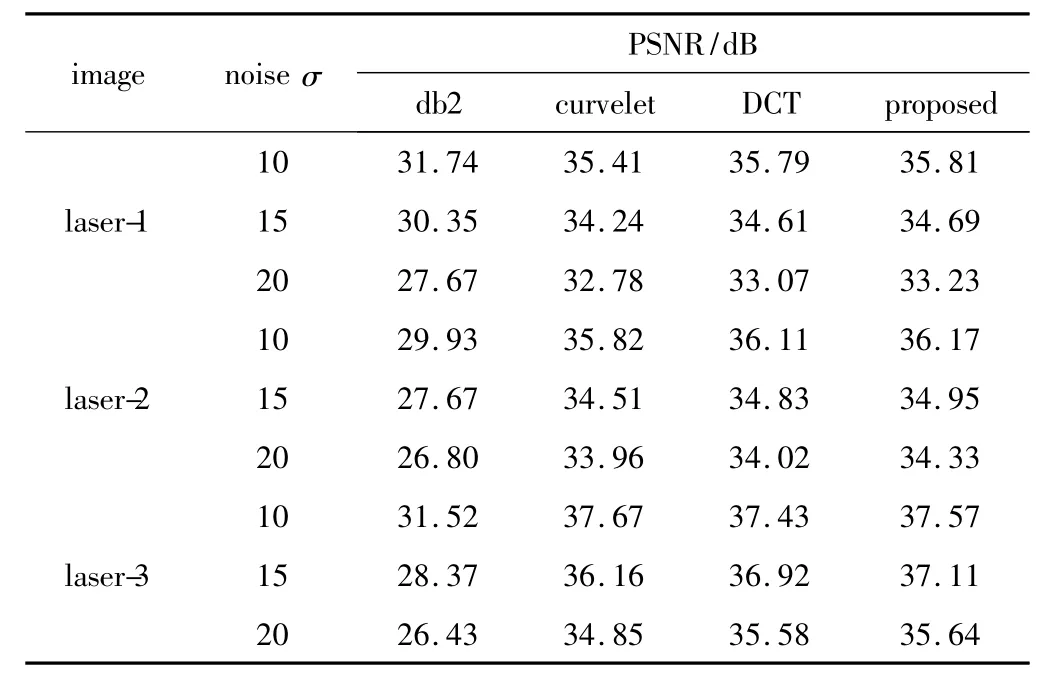
Table 1 Comparison of PSNR of four de-noising methods

Table 2 Comparison of HSSIM of four de-noising methods

對實驗圖像添加σ=20的白噪聲，分別采用上述4種方法處理后的效果如圖1～圖3所示。由圖可見，從主觀視覺效果上來看，本文中算法要優于其它3種方法。由上述分析可知，在不同的噪聲條件下，針對不同的圖像，本文中算法均具有較好的去噪能力和較強的魯棒性。

4 結論

基于稀疏表示理論，提出了一種以相似因子取代重構誤差平方和，以殘差比閾值替代硬閾值來實現稀疏分解的算法。實驗結果表明，從PSNR，HSSIM等客觀評價標準和主觀視覺效果兩個方面來看，本文中算法均具有較好的去噪能力和較強的魯棒性。對字典進行優化設計和對閾值條件進行改進將是下一步的研究方向。

［1］ ZHANG H X.Study on building modeling based on 3-D laser scanning technology［J］.Laser Technology，2014，38(3):431-434(in Chinese).

［2］ XU Y F，XU J，ZHAO F L，et al.Laser active image denoising method based on wavelet transform［J］.High Power Laser and Particle Beams，2009，21(12):1786-1790(in Chinese).

［3］ CAI Z M，LAI J H.An over-complete learned dictionary-based image de-noising method［J］.Acta Electronica Sinica，2009，37(2):347-350(in Chinese).

［4］ ELAD M，AHARON M.Image denoising via sparse and redundant representations over learned dictionaries［J］.IEEE Transactions on Image Processing，2006，12(15):3736-3745.

［5］ WU U Q，LI L.Image denoising using kernel fuzzy clustering and regularization on sparse model［J］.Acta Photonica Sinica，2014，43(3):1-7(in Chinese).

［6］ WANG C，SU W M，GU H，et al.SAR image despeckling based on morphological component analysis［J］.Chinese Journal of Radio Science，2013，28(3):448-454(in Chinese).

［7］ WEI Y L，WEN X B，ZHOU Y L，et al.New self-adaptive method for image denoising based on sparse decomposition and clustering［J］.Journal of Computer Applications，2013，33(2):476-479(in Chinese).

［8］ MA L，DENG C Z，WANG S Q，et al.Feature-retained image denoising via sparse representation［J］.Journal of Computer Applications，2013，33(5):1416-1419(in Chinese).

［9］ DABOV K，FOI A，KATAKOVIK V，et al.Image denoising by sparse 3-D transform-domain collaborative filtering［J］.IEEE Transactions on Image Processing，2007，16(8):2080-2095.

［10］ FANG L Y，LI S T，MCNABB R，et al.Fast acquisition and reconstruction of optical coherence tomography images via sparse representation［J］.IEEE Transactions on Medical Imaging，2013，32(11):2034-2049.

［11］ AHARON M，ELAD M，BRUCKSTEIN.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation［J］.IEEE Transactions on Image Processing，2006，54(11):4311-4322.

［12］ ZHU L，LI Q L，ZHANG T，et al.Metric of image quality based on structural simnarity［J］.Opto-Electronic Engineering，2007，34(11):108-113(in Chinese).

［13］ LIANG W，QUE P W，CHEN L，et al.Residual ratio iteration termination condition for MP method［J］.Journal of Shanghai Jiaotong University，2010，44(2):171-175(in Chinese).