基于DS數據融合與SVR-PF的鋰離子電池RUL預測方法

王常虹，董漢成，凌明祥，李清華

?

基于DS數據融合與SVR-PF的鋰離子電池RUL預測方法

王常虹，董漢成，凌明祥，李清華

(哈爾濱工業大學 空間控制與慣性技術研究中心，黑龍江 哈爾濱 150001 )

為防止鋰離子電池失效導致的系統失效，提出一種基于DS數據融合與支持向量回歸機粒子濾波(Support Vector Regression-Particle Filter，SVR-PF)的鋰離子電池剩余有效工作時間(Remaining Useful Life，RUL)預測方法.結果表明：該預測方法能夠融合不同數據源對鋰離子電池RUL的預測結果，改進可用數據較少時RUL的預測準確度.

鋰離子電池； RUL； DS數據融合； SVR-PF

0 引言

鋰離子電池被廣泛應用于各種電子設備，為設備的正常運行提供必要的能源[1-2].電池的剩余有效工作時間(Remaining Useful Life，RUL)定義為在一個特定的運行條件下，電池從當前運行狀態衰退至無法正常工作狀態所需要的RUL，為電池視情維護(Condition Based Maintenance，CBM)的重要指標[3].因此，尋找一個可靠且準確的途徑預測鋰離子電池的RUL，可以提供鋰離子電池系統維護或更換的相關信息[4-5].

數據驅動算法(Data-driven Algorithm)可以利用實測電池數據建立電池的回歸模型，用于鋰離子電池RUL預測[6].Juan Carlos Alvarez Anton等[7]應用支持向量回歸機(Support Vector Regression，SVR)，分析鋰離子電池荷電狀態與電池電壓、電流、溫度的關系，建立估計電池使用狀態的數據驅動模型，分析電池的健康狀態(State-of-Health，SoH)，預測電池的RUL.Weng Caihao[8]與Adnan Nuhic[9]等利用支持向量回歸機，建立電池的健康狀態(State of Health,SoH)模型，即電池容量與充放電周期、電池開路電壓的關系，預測電池性能衰退與RUL.遞歸濾波算法(Recursive Filter Algorithm)基于電池狀態空間模型，可以利用實測電池數據分析、估計與預測電池的故障，用于鋰離子電池RUL預測[10].Dare Andre等[11]建立含有無跡卡爾曼濾波器(Unscented Kalman Filter，UKF)與卡爾曼濾波器的雙濾波器估計模型，利用鋰離子電池的電壓、電流與充放電周期數估計電池的剩余容量與荷電狀態，預測鋰離子電池的RUL.He Wei[12]與Miao Qiang[13]等將衛星鋰離子電池的容量作為分析參數，對容量隨時間衰退的特性進行數據挖掘，建立衰退趨勢方程，以估計容量隨時間的衰退趨勢，估計鋰離子電池的當前工作狀態，預測鋰離子電池的RUL.Bhaskar Saha等[14]應用向量機平滑后得到的阻抗數據與容量數據，分析衛星鋰離子電池性能隨時間衰退的趨勢，預測鋰離子電池的RUL.

鋰離子電池的RUL預測需要分析可用數據，以估計電池的當前狀態，預測電池性能的衰退趨勢，在可用數據量很少時，鋰離子電池RUL的預測準確度降低，現有文獻未提出有效解決方法.筆者采用基于阻抗的鋰離子電池RUL預測方法[15]、基于容量的鋰離子電池RUL預測方法[16]，以及提出的基于DS數據融合理論(Dempster-Shafer Theory)與支持向量回歸機粒子濾波(Support Vector Regression-Particle Filter，SVR-PF[15])的預測方法，融合不同數據源對鋰離子電池RUL分析結果，比較3種方法的預測性能，以在可用數據較少時得到準確的預測結果.

1 DS數據融合

1.1 理論

DS數據融合理論(Dempster-Shafer Theory)[17]利用基本概率賦值 (Basic Probability Assignment，BPA) 函數對來自不同源的數據進行融合，對辨識框架(Frame of Discernment)中所有可能發生的命題進行可信度(Belief)分析，利用融合規則結合所有命題發生的可信度，從而達到數據融合的目的.

設m1與m2為在辨識框架中兩個BPA函數，m1,2為融合后的BPA函數，則DS數據融合可以表示為

m1,2(?)=0,

(1)

(2)

其中

(3)

DS數據融合理論結合對同一問題不同源的相同觀點，同時剔除所有的沖突觀點，可以得到更加可靠的融合后驗BPA函數.

1.2 應用

基于DS數據融合的鋰離子電池RUL預測具有兩個數據源：(1)利用阻抗數據的RUL預測；(2)利用容量數據的RUL預測.筆者提出的基于DS數據融合與SVR-PF的鋰離子電池RUL預測融合兩種方法得到的預測結果，最終得到融合預測結果.

將全集即辨識框架Ω記為

Ω={im,cap},

(4)

則冪集2Ω為

2Ω={?,{im},{cap},{im∪cap}},

其中冪集2Ω中所有命題的含義為

(1){im}代表利用阻抗數據預測得到的RUL可信度；

(2){cap}代表利用容量數據預測得到的RUL可信度；

(3){im∪cap}代表利用阻抗或容量數據預測得到的RUL可信度.

同時，定義在冪集2Ω上的BPA函數m1與m2代表的含義為

(1)m1為利用阻抗數據對RUL進行預測時對冪集2Ω中命題的可信度分配；

(2)m2為利用容量數據對RUL進行預測時對冪集2Ω中命題的可信度分配.

基于DS數據融合的BPA函數結合方式見表 1，其中x=m1(im∪cap)m2(im∪cap).

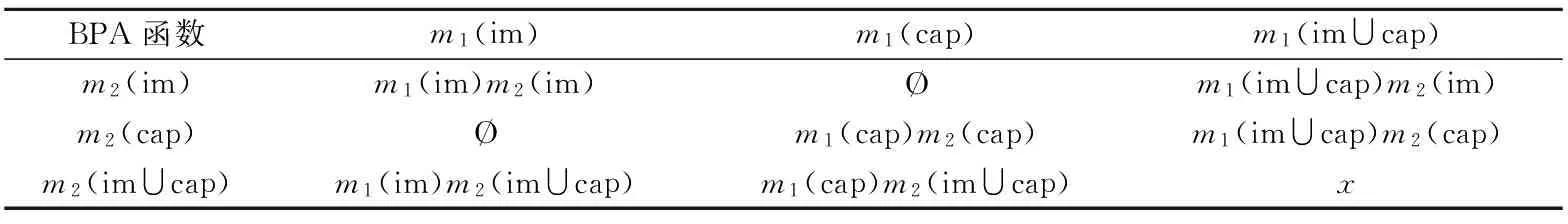
表1 基于DS數據融合的BPA函數結合方式Table 1 The combination of BPA function based on DS theory

基于表 1，可以得到數據融合后的后驗BPA函數m為

(6)

(7)

其中

a=m1(im)m2(im)+m1(im∪cap)m2(im)+m1(im)m2(im∪cap),

(8)

b=m1(cap)m2(cap)+m1(im∪cap)m2(cap)+m1(cap)m2(im∪cap),

(9)

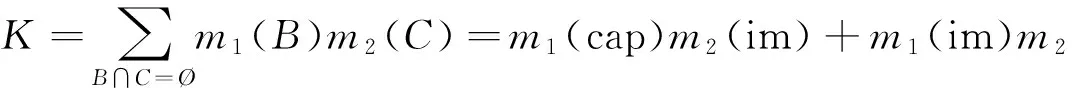
(10)

由此得到DS數據融合在鋰離子電池RUL預測中方法，利用后驗融合BPA函數式與將兩類方法的預測結果結合，以得到更加準確的預測結果.

2 實測鋰離子電池阻抗與容量數據

所用鋰離子電池阻抗與容量數據在美國愛達荷國家實驗室(IdahoNationalLaboratory)測得[18].實驗用鋰離子電池型號為Gen2 18650-size，實驗在室溫(24 ℃)與43 ℃溫度條件下恒溫進行，分為3個循環的測試階段：(1)充電:1.5A恒流充電至電壓4.2V，隨后恒壓充電至電流20mA；(2)放電：2.0A電流恒壓放電至電壓2.5V；(3)阻抗：進行0.1～5.0kHz掃頻，得到電化學阻抗譜，進而得到電池阻抗.

共用4塊電池.電池5、6與7的實測數據見圖1，在室溫(24 ℃)條件下恒溫測得；電池32的實測數據見圖2，在43 ℃溫度條件下恒溫測得.由圖1-2可以看出，鋰離子電池容量隨著充放電周期的增加而減少，阻抗隨著充放電周期的增加而增加.利用測得的電池數據驗證文中提出的鋰離子電池RUL預測方法的性能.

圖1 電池5、6、7容量與阻抗數據Fig.1 Capacity and impedance data of battery 5,6 and 7

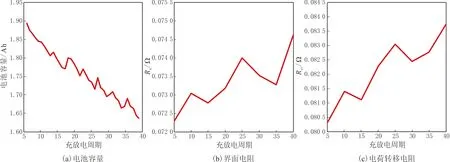
圖2 電池32容量與阻抗數據Fig.2 Capacity and impedance data of battery 32

持續的充放電過程加速電池的性能衰退，同時阻抗測試提供電池內部參數的變化方式.當電池達到壽命終點時實驗停止，將電池達到壽命終點(EndofLife，EOL)時容量占標稱容量的百分比稱為EOL門限.由于各個電池停止實驗時的容量值不同，因此EOL門限也不同，電池5、6、7、32的EOL門限分別為70%、65%、75%、95%.

3 基于DS數據融合與SVR-PF的鋰離子電池RUL預測方法

3.1 預測過程

3.1.1 初始狀態

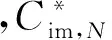
(1)首先分析BPA函數m1,i(im)的初值，由中心極限定理可知，大量的阻抗數據測量誤差服從正態分布，即

(11)

(12)

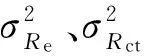
由文獻[15]可知：

(13)

因此容量估計Cim,N服從正態分布，即

(14)

其中

μCim,N=αN(μRe,N+μRct,N)+βN=CN,

(15)

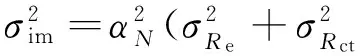
(16)

由此得到BPA函數m1,i(im)的初值m1,N+1(im)為

(17)

(2)然后計算BPA函數m2,i(cap)，同樣由中心極限定理可知，大量的容量數據測量誤差服從正態分布，即

(18)

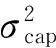
μCcap,N=CN,

(19)

則BPA函數m2,i(cap)的初值m2,N+1(cap)為

(20)

在得到BPA函數m1,N+1(im)與m2,N+1(cap)值后，對其他的BPA函數值進行分析.由于兩類預測方法沒有關聯，可得

m1,N+1(cap)=m2,N+1(im)=0.

(21)

根據BPA函數的性質可得

m1,N+1(im∪cap)=1-m1,N+1(im)-m1,N+1(cap)=1-m1,N+1(im),

(22)

m2,N+1(im∪cap)=1-m2,N+1(im)-m2,N+1(cap)=1-m2,N+1(cap).

(23)

(3)在確定所有的BPA函數值后，計算后驗融合BPA函數值，將融合后的BPA函數表示為m，由式(6)與式(7)可知：

(24)

其中

(25)

其中

m1,N+1(im)m2,N+1(cap)=m1,N+1(im)m2,N+1(cap).

(26)

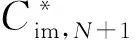
(27)

由此得到基于DS數據融合與SVR-PF鋰離子電池RUL預測的初始狀態，即

Initial=[m1,N+1(im),m1,N+1(cap),m1,N+1(im∪cap),m2,N+1(im),m2,N+1(cap),

(28)

3.1.2 預測過程

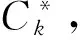
(29)

(30)

由于兩類預測模型沒有關聯，可知

m1,k+1(cap)=m2,k+1(im)=0.

(31)

基于BPA函數性質，有

m1,k+1(im∪cap)=1-m1,k+1(im),

(32)

m2,k+1(im∪cap)=1-m2,k+1(cap).

(33)

步驟2：預測第k+1個充放電周期的容量值.由式(6-7)、式(29-33)可知，后驗融合BPA函數mk+1(im)與mk+1(cap)為

(34)

(35)

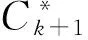
(36)

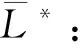
(37)

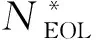
3.2 預測模型

建立基于DS數據融合與SVR-PF的鋰離子電池RUL預測模型：

(38)

其中狀態Xk為

(39)

式中：Xim,k為利用阻抗數據分析得到的狀態；Xcap,k為利用容量數據分析得到的狀態；XDS,k為利用DS數據融合分析得到的狀態，并且有

(40)

(41)

(42)

式(40-42)中：λR,k為第k個充放電周期辨識出的阻抗衰退參數[15]；R1,k、λR1,k、R2,k和λR2,k為在第k個充放電周期的基于容量數據分析得到的容量衰退參數[16]；*為對應變量的預測值.

由此，結合文獻[15-16]RUL預測模型，可得預測模型式(38)的狀態方程，其中利用阻抗數據分析的部分狀態方程為

(43)

式中：αN、βN為第N個充放電周期的基于阻抗數據分析得到的容量衰退參數估計值.

利用容量數據分析的部分狀態方程：

(44)

利用DS數據融合的部分狀態方程：

(45)

組合式(43-45)得到預測模型式(38)的狀態方程，式(38)的測量方程表示為

(46)

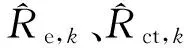
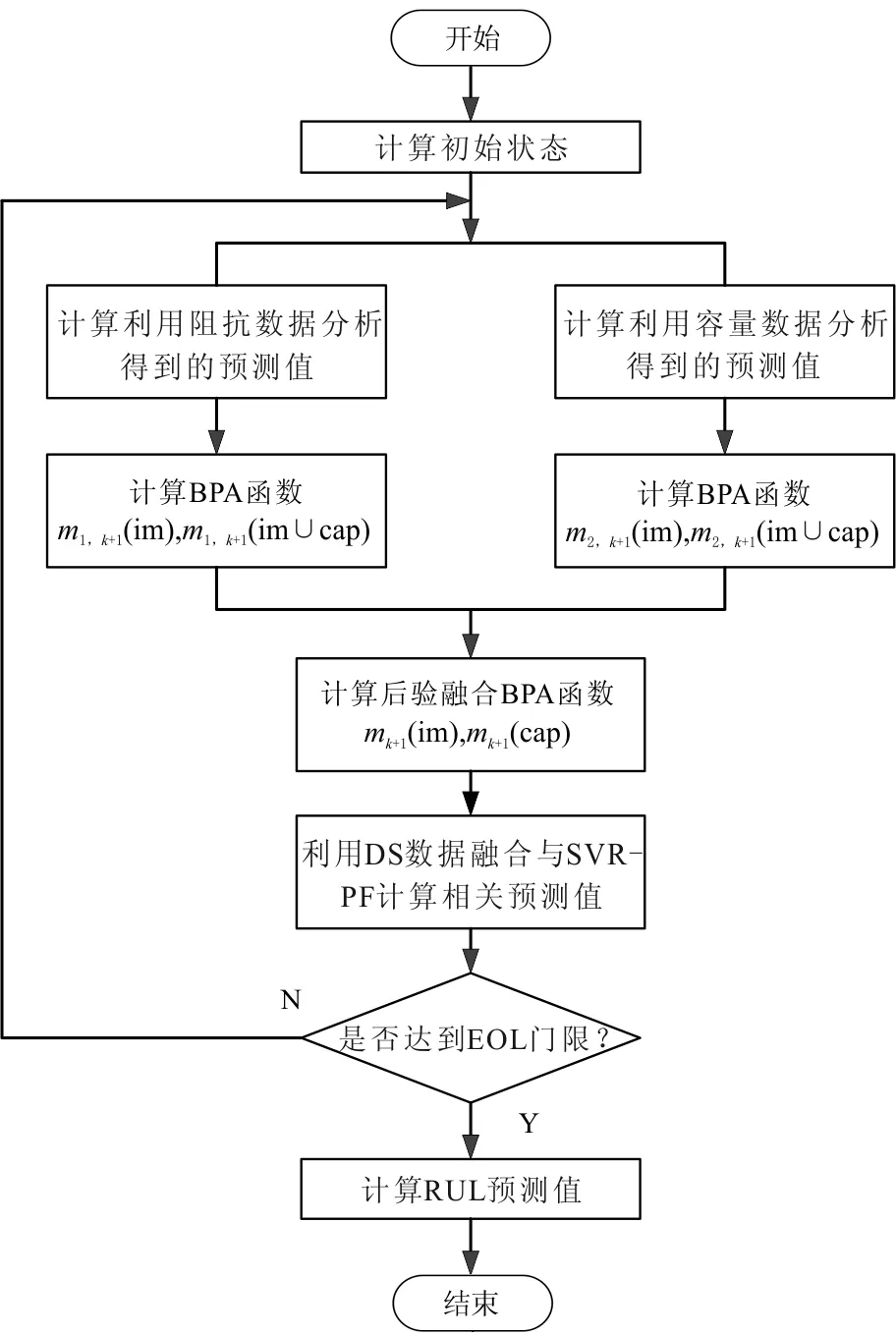
圖3 基于DS數據融合與SVR-PF的鋰離子電池RUL預測方法流程Fig.3 Process of Lithium-ion battery RUL prediction based on DS theory and SVR-PF

綜上所述，基于DS數據融合與SVR-PF的鋰離子電池RUL預測方法流程見圖3.

4 仿真實例

為了對比提出的基于DS數據融合與SVR-PF的鋰離子電池RUL預測方法，與文獻[15]利用阻抗的RUL預測方法和文獻[16]利用容量的RUL預測方法在可用數據較少時的RUL預測性能，應用電池5、6、7、32的數據.將電池5、6、7、32的RUL預測門限分別設為90%、85%、95%、95%標稱容量.RUL預測門限值定義為低于電池最大容量(100%)的百分比，其對應容量高于電池EOL門限對應容量.高RUL預測門限使得算法用于分析電池健康狀態的數據變少，使用條件變得苛刻，以檢驗算法在可用數據較少時的性能.

電池RUL與EOL的預測結果見表2.電池RUL與EOL的誤差預測結果見表3.3種方法的電池5、6、7、32的數據預測結果見圖4-7.

由表2-3和圖4-7可知，文中提出的基于DS數據融合與SVR-PF的RUL預測方法比文獻[15]與文獻[16]方法的預測結果更準確，具有更小的預測誤差.原因是提出的基于DS數據融合與SVR-PF的RUL預測方法可以融合另外2種方法的預測結果，相對于單一方法的預測結果更加可靠.

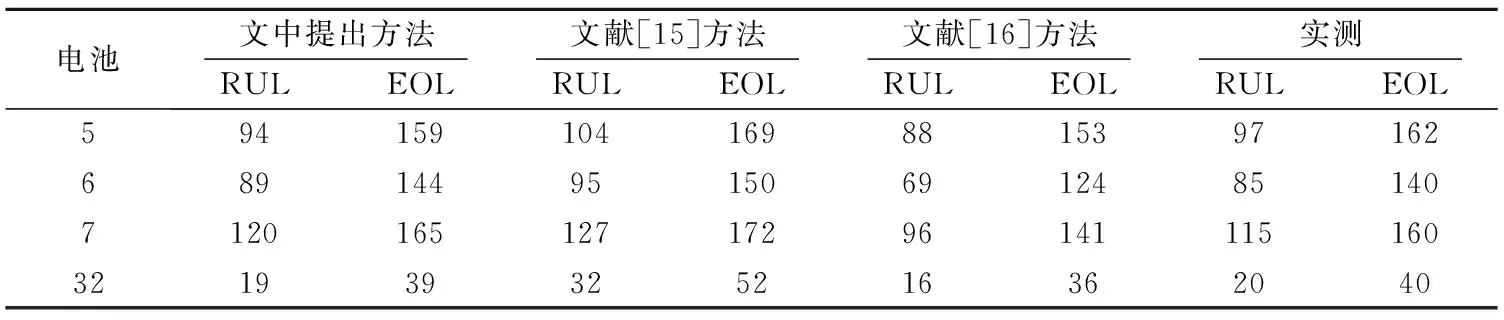
表2 3種方法電池的RUL與EOL預測結果 充放電周期Table 2 RUL and EOL prediction results of the 3 methods %

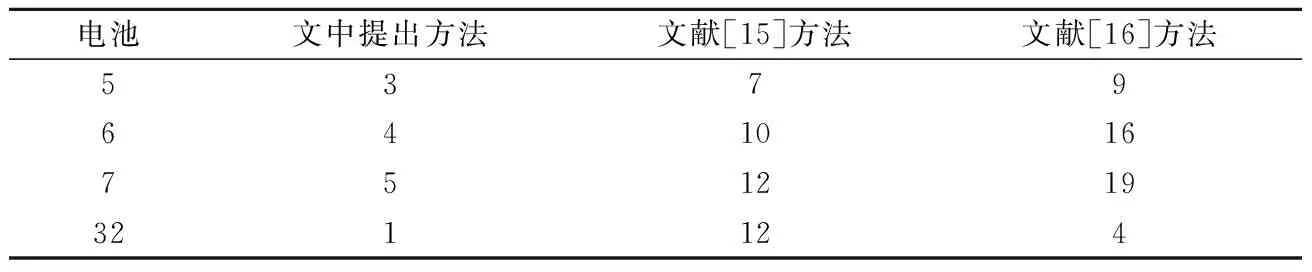
表3 3種方法電池的RUL與EOL預測誤差結果 充放電周期Table 3 RUL and EOL prediction errors of the 3 methods %

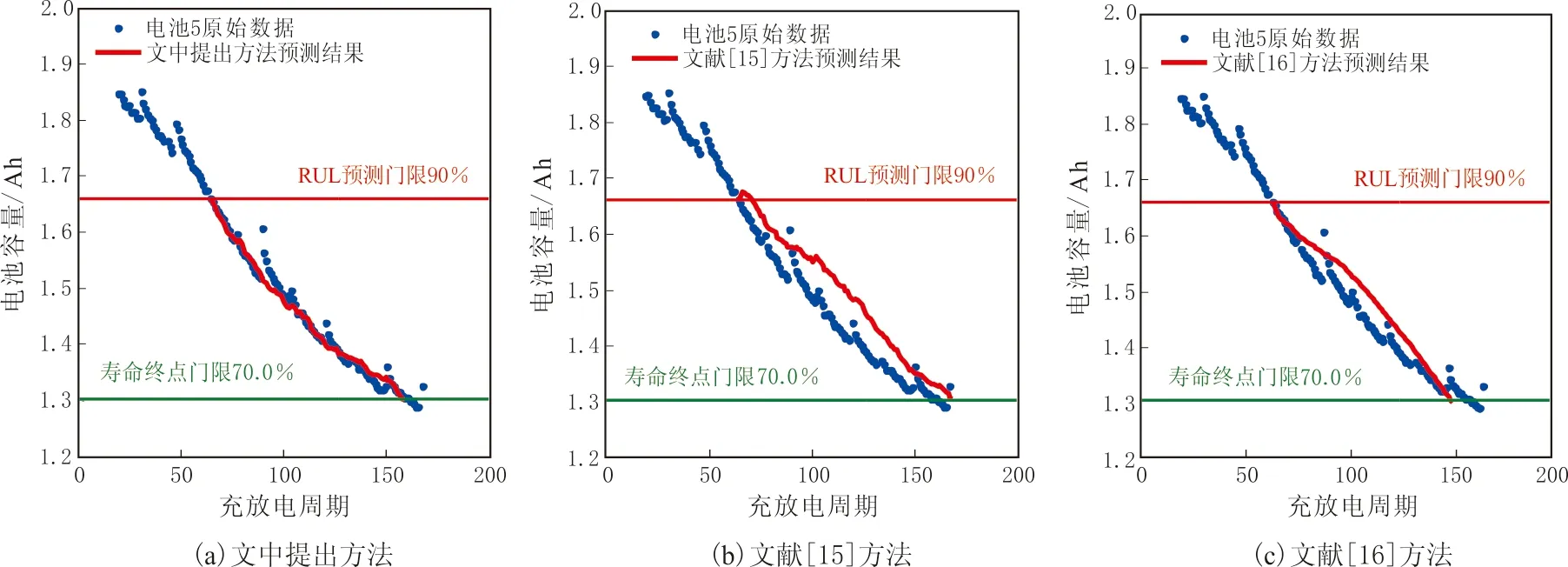
圖4 電池5的3種方法預測數據Fig.4 Battery 5 prediction results of the 3 methods

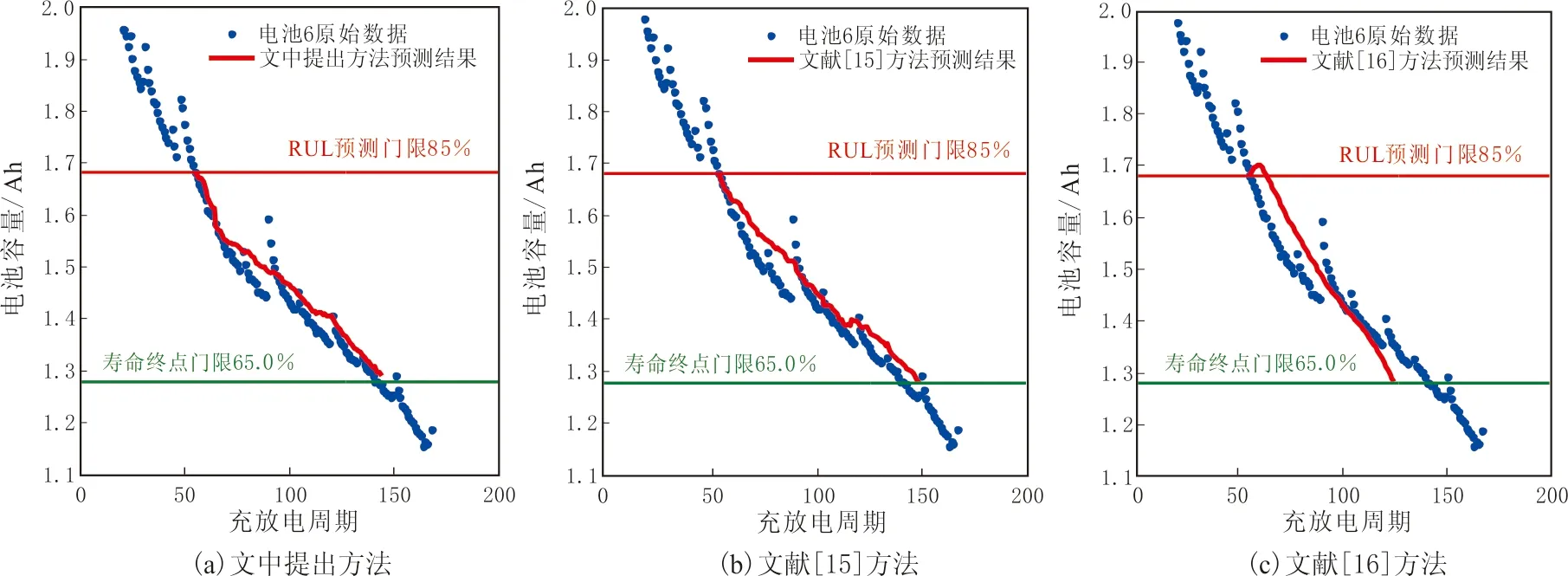
圖5 電池6的3種方法預測數據Fig.5 Battery 6 prediction results of the 3 methods

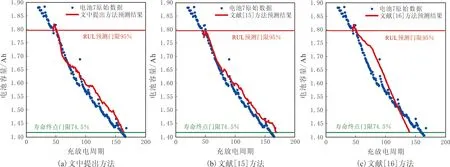
圖6 電池7的3種方法預測數據Fig.6 Battery 7 prediction results of the 3 methods

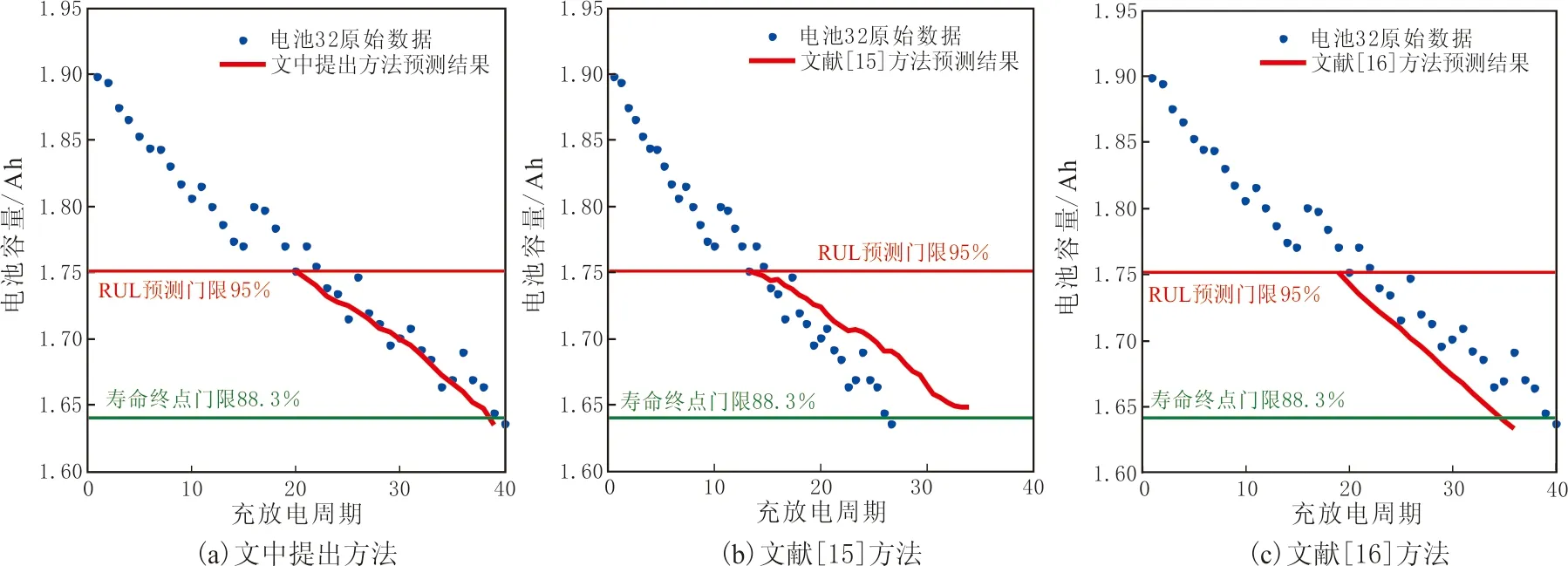
圖7 電池32的3種方法預測數據Fig.7 Battery 7 prediction results of the 3 methods

5 結束語

提出一種基于DS數據融合與SVR-PF的鋰離子電池RUL預測方法，它有效結合利用阻抗數據與利用容量數據的RUL預測方法，使得RUL預測過程更加可靠.在可用數據較少時，與利用阻抗和利用容量的RUL方法相比鋰離子電池RUL預測結果更加準確.

[1] Lu Languang, Han Xuebing, Li Jianqiu, et al.A review on the key issues for lithium-ion battery management in electric vehicles [J].Journal of Power Sources, 2013,226(1):272-288.

[2] Xing Yinjiao, Eden W M, Tsui K L, et al.Battery management systems in electric and hybrid vehicles [J].Energies, 2011,4(12):1840-1857.

[3] Si Xiaosheng, Wang Wenbin, Hu Changhua, et al.Remaining useful life estimation-a review on the statistical data driven approaches [J].European Journal of Operational Research, 2011,213(1):1-14.

[4] Wang Dong, Miao Qiang, Michael P.Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model [J].Journal of Power Sources, 2013,239(1):253-264.

[5] Eddahech A, Briat O, Woirgard E, et al.Remaining useful life prediction of lithium batteries in calendar ageing for automotive applications [J].Microelectronics Reliability, 2012,52(1):2438-2442.

[6] Seyed Mohammad Rezvanizaniani, Liu Zongchang, Chen Yan, et al.Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (Ev) safety and mobility [J].Journal of Power Sources, 2014,256(1):110-124.

[7] Juan Carlos Alvarez Anton, Paulino Jose Garca Nieto, Cecilio Blanco Viejo, et al.Support vector machines used to estimate the battery state of charge [J].IEEE Transactions on Power Electronics, 2013,28(12):5919-5926.

[8] Weng Caihao, Sun Jing, Peng Huei.A unified open-circuit-voltage model of Lithium-Ion Batteries for State-of-Charge estimation and State-of-Health monitoring [J].Journal of Power Sources, 2014,258(1):228-237.

[9] Adnan Nuhic, Tarik Terzimehic, Thomas Soczka-Guth, et al.Health diagnosis and remaining useful Life prognostics of lithium-ion batteries using data-driven methods [J].Journal of Power Sources, 2013,239(1):680-688.

[10] Gregory L P.Extended Kalman filtering for battery management systems of lipb-based hev battery packs [J].Journal of Power Sources, 2004,134(2):252-292.

[11] Dave Andre, Christian Appel, Thomas Soczka-Guth, et al.Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries [J].Journal of Power Sources, 2013,224(1):20-27.

[12] He Wei, Nicholas Williard, Michael Osterman, et al.Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the bayesian Monte Carlo method [J].Journal of Power Sources, 2011,196(1):10314-10321.

[13] Miao Qiang, Xie Lei, Cui Hengjuan, et al.Remaining useful life prediction of lithium-ion battery with unscented particle filter technique [J].Microelectronics Reliability, 2013,53(1):805-810.

[14] Bhaskar Saha, Kai Goebel, Scott Poll, et al.Prognostics methods for battery health monitoring using a bayesian framework [J].IEEE Transactions on Instrumentation and Measurement, 2009,58(2):291-296.

[15] Dong Hancheng, Jin Xiaoning, Lou Yangbing, et al.Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector Regression-Particle filter [J].Journal of Power Sources, 2014,2014(1):114-123.

[16] 王常虹,董漢成,凌明祥,等.車用鋰離子電池剩余有效工作時間預測方法[J].汽車工程,2015,37(4):476-479.Wang Changhong, Dong Hancheng, Ling Mingxiang, et al.Remaining useful life prediction of automotive lithium-ion battery [J].Automotive Engineering, 2015,37(4):476-479.

[17] Priyanka Aggarwal, Deepak Bhatt, Vijay Devabhaktuni.Dempster shafer neural network algorithm for land vehicle navigation application [J].Information Sciences, 2013,253:26-33.

[18] Kai Goebel Bhaskar Saha, Jon Christophersen.Comparison of prognostic algorithms for estimating remaining useful life of batteries [J].Transactions of the Institute of Measurement and Control, 2009,31(3):293-308.

2015-04-27；編輯：任志平

國家自然科學基金項目(61375046)；中央高校基本科研業務費專項基金項目(HIT.NSRIF 2014031)

王常虹(1961-)，男，博士，教授，主要從事智能控制與智能系統方面的研究.

TM912

A

2095-4107(2015)04-0109-10

DOI 10.3969/j.issn.2095-4107.2015.04.014