基于正態分布和兩參數威布爾分布的風速曲線擬合方法研究
張盼盼
(貴州大學,貴州 貴陽 550025)
?
基于正態分布和兩參數威布爾分布的風速曲線擬合方法研究
張盼盼
(貴州大學,貴州 貴陽 550025)
以日常生活中常用到的正態分布和兩參數威布爾分布擬合實際的風速數據,采用最大似然估計法得到兩種分布的相關參數值,并在此基礎上以這兩種分布的概率密度函數和分布函數圖與風速數據的頻率直方圖做對比,以此分析哪種分布函數模擬風速分布的效果比較理想,得到的結果是兩參數威布爾分布可以認為是擬合風速較好的模型。
正態分布,兩參數威布爾分布,概率密度函數
1 引言
風能作為風力發電的基礎,以其清潔性和可再生性受到越來越廣泛的應用。風速分布模型的確立,可以更好地進行配電網的可靠性評估和風電場的容量選址分析。但風能本身存在著間歇性和不穩定性的缺點使得風速也存在著不穩定性。因此有必要對風速的分布模型進行更進一步的研究。通常情況下描述風速分布模型的有瑞利分布、正態分布和兩參數威布爾分布。瑞利分布因其應用于風速低于3.6m/s的范圍內,且誤差較大,所以瑞利分布不被認為是用來描述風速的理想分布模型。相比之下,正態分布和兩參數威布爾分布應用則較廣泛。國內對應用正態分布和兩參數威布爾分布描述風速分布也做了一些研究。文獻[1]認為當形狀參數k>3.5時,風速的分布可以用正態分布來描述,并以正態分布建立風速負荷二元正態聯合分布函數,并進一步評估配電網的可靠性。文獻[2]比較了威布爾分布參數的三種算法,并以計算得到的三種參數值擬合風速曲線。文獻[3]采用四種不同方法求取威布爾分布參數。文獻[4]也采用三種算法求取威布爾分布參數,并應用威布爾擬合曲線分析希尼爾水庫風能情況。文獻[5]采用最大似然估計了對數正態分布的參數。上述文獻只選擇了一種分布模型去擬合風速曲線,但基于風速的時變性和各地情況的特殊性,本文以正態分布和威布爾分布這兩種分布模型分別對風速進行擬合,對擬合的結果進行對比分析從而得到描述風速的理想分布模型。
2 正態分布模型
正態分布(高斯分布)是一種在工程領域中經常應用到的概率分布模型。假設變量X服從具有兩個參數μ和σ2的正態分布,記X服從正態分布N(μ,σ2),那么此正態分布的概率密度函數為:
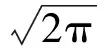
(1)
其中,參數μ為正態分布的期望,σ2為正態分布的方差。當μ=0,σ2=1時,稱變量X服從標準正態分布。只有確定兩個參數μ和σ2值后,風速的正態分布概率密度函數解析式才能唯一確定。常用的正態分布參數值估計方法有多種,本文采用最大似然估計法求取參數值μ和σ2。
3 威布爾分布模型
威布爾分布是目前被認為是描述風速分布比較理想的模型,它主要應用于可靠性分析中。威布爾分布的概率密度函數為:
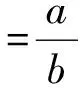
(2)
其中,參數a稱為威布爾分布的形狀參數,b稱為威布爾分布的比例參數。以威布爾分布模擬風速分布時,首先要確定參數a和b的值。常用參數值的確定方法有HOMER軟件法、最小二乘法和最大似然估計,本文同樣采用最大似然估計威布爾分布參數值。
4 最大似然估計法
設X為總體,X1,X2,X3,…,Xn為來自的樣本,x1,x2,x3,…,xn是相應于樣本的一個樣本值,那么X1,X2,X3,…,Xn等于x1,x2,x3,…,xn這個事件的概率為:
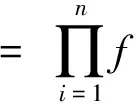
(3)
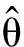
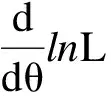
(4)
5 模型的建立
以某地一年風速數據為樣本值輸入matab中,采用最大似然估計法求得的正態分布的期望和方差值如表1所示,參數置信區間為90%。

表1 正態分布參數值
把表1數據代入公式(1)得到風速分布的正態分布模型解析式如公式(5)所示。
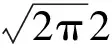
(5)
在matlab中輸入風速數據,采用最大似然估計法求得威布爾分布的兩個參數值a和b如表2所示,參數置信區間為90%。

表2 兩參數威布爾分布參數值
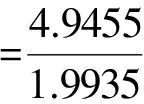
(6)
6 風速曲線擬合仿真
根據公式(5)和(6)所確定的解析式擬合風速數據,通過matlab編制程序得到正態分布概率密度函數擬合曲線和威布爾分布概率密度函數擬合曲線如圖1所示。
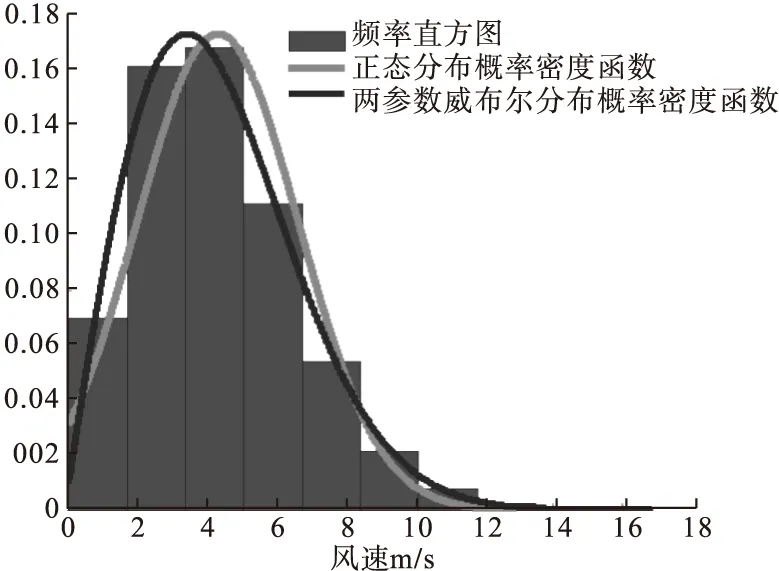
圖1 正態分布和兩參數威布爾分布概率密度函數圖
正態分布函數擬合曲線和兩參數威布爾分布函數擬合曲線如圖2所示。
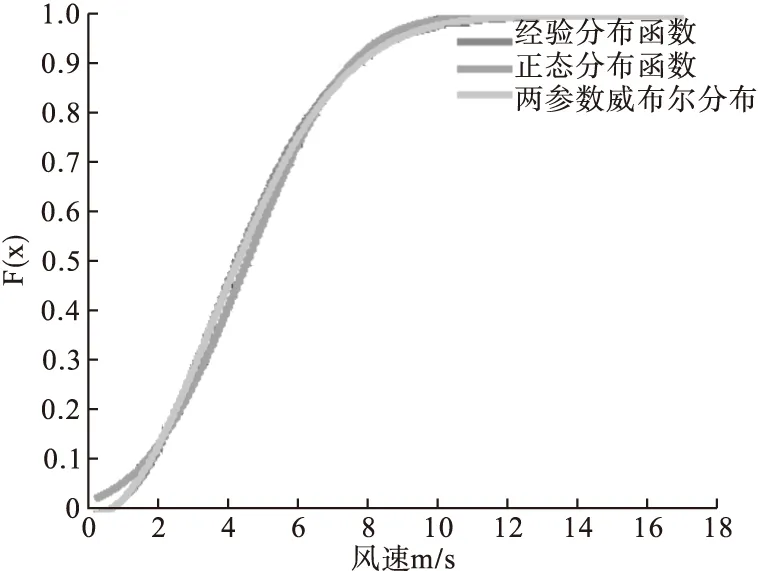
圖2 正態分布和兩參數威布爾累積分布函數圖
從圖2可以看出,兩參數威布爾函數分布與樣本的經驗分布函數擬合的效果相對于正態分布函數擬合的效果要好。
7 結論
從本文所得結果可以看出,兩參數威布爾分布可以認為是描述實際風速分布較好的模 型,采用最大似然估計法求取分布函數中的未知參數,這樣可以減少采用其它方法所存在的計算工作量。從圖中可見正態分布模擬風速分布曲線的誤差還是比較大的,所以在通常情況下,我們采用兩參數威布爾分布來模擬風速分布。風速分布模型的確立可以為含分布式電源的配電網可靠性分析提供依據,從而提高可靠性分析的準確度和可信度。
[1] 孫若笛.計及風速與負荷時序相關性的配電網可靠性評估[D].重慶:電氣工程學院,2012.
[2] 徐衛民,孔森紅,魏保玉.三種風速威布爾分布參數算法的比較[C]//第26屆中國氣象學會年會氣候資源應用研究分會場論文集,2009:141-143.
[3] 包小慶,劉志強,吳永忠,等.雙參數威布爾分布函數的確定及曲線擬合[J].能源與環境,2007:4-9.
[4] 魏光輝,申蓮,何玉春.雙參數威布爾分布函數在希尼爾水庫風速資料分析中的應用[J].沙漠與綠洲氣象,2008:38-39.
[5] 于洋,孫月靜.對數正態分布參數的最大似然估計[J].九江學院學報,2007:55-57.
[6] 盛驟,謝式千.概率論與數理統計[M].北京:高等教育出版社,2008:152-153.
Research on the fitting Method of Wind Curves Based on Normal Distribution and Two Parameter Weibull Distribution
ZHANGPan-pan
(Guizhou University,Guiyang 550025,China)
Take normal distribution and two parameter weibull distribution in everyday life to fit actual wind speed data,adopt maximum quasi-nature method of estimation to get relevant parameters of the two kinds of distrubitions,and on the basis of this,compare the probability density function and distribution density arrangement of these two distributions with the frequency histogram of the wind speed data.For this reason,we analyze which distribution function simulation wind speed distribution is more ideal.The result is that two parameter weibull distribution is to be considered as the fitting wind speed model better.
normal distribution;two parameter weibull distribution;probability density function
1004-289X(2015)04-0047-03
TM61
B
2014-09-25

