適用于環境監測中的低空遙感影像匹配方法
張瑩
(天津市環境監測中心,天津300191)
1 引言
近年來,我國自然災害頻繁發生,生活環境在不同方面造成了巨大的損失,因此需要及時對環境進行監測,掌握災害發生情況。為了提高災害監測效率,必須提供準確的災害信息,而以傳統的影像獲取平臺為基礎的環境監測方法在分辨率及時間上難以滿足救災應急的需要。無人駕駛低空飛行器及其輔助設備的發展,彌補了傳統航空攝影測量的缺陷,使得低空遙感在大比例尺遙感影像應用方面,迅速成為了廣泛關注的熱點[1]。
目前,對于航天航空遙感影像的匹配研究較多,也有了較為成熟的匹配算法并獲得了理想的匹配結果,但是對于低空遙感影像匹配的研究卻較少。本文研究的目的就是尋找一種匹配算法,能夠適用于低空遙感影像數據處理。
本文從特征檢測和特征描述兩方面進行,涉及到的算法主要有 MSER 算法[2](Maximally Stable Extremal Regions)、SIFT 算法[3,4](Scale-invariant feature transform)以 及 SURF 算 法[5](Speeded Up Robust Features)。
2 特征提取及描述
2.1 MSER檢測算法
相關實驗證明,MSER檢測算法在各種不同條件下進行實驗時,均顯示出其穩定的仿射不變性。MSER算法的基本思想為,對于一幅灰度影像定義一系列閾值t,閾值t的范圍在0~255內,將影像中每個點的灰度值分別與該閾值進行比較,灰度值大于t的像素點重采樣為1,將灰度值小于t的像素點重采樣為0,最終得到256幅二值圖像。對閾值相鄰的二值圖像檢測出特征區域并對面積進行比較,獲取特征區域面積隨閾值變化的關系。最后選取出適當個數的特征區域面積隨閾值變化較小的區域即為最大穩定極值區域(MSER)。這樣,MSER算法獲取的區域就具有以下特點。
(1)當影像整體發生相同的亮度變化時,MSER算法獲取的極值區域是穩定的。
(2)檢測出的特征保留了拓撲性,特征區域內的像素點即使發生了幾何變化,如縮放、平移或者旋轉等現象,發生變換后依然還在同一個特征區域內。
(3)區域特征本身的優點就是在一個允許的范圍內,如果影像發生了幾何、光照變換等現象,特征區域依然能夠保持較好的不變性。
2.2 SIFT算法
SIFT算法是David G.Lowe等人于1999年提出,并于2004年提高完善的一種基于尺度空間的方法,是目前影像匹配領域研究的重點和熱點。SIFT特征匹配主要分為3個步驟:特征提取、特征描述、特征匹配。
2.2.1 SIFT特征提取
SIFT算法是基于影像特征尺度選擇的思想,首先要建立影像的尺度空間,在不同尺度下檢測出對尺度縮放、旋轉、亮度變化無關的特征點后,確定特征點的位置,對特征點進行描述進而進行影像匹配。Koenderink[6]和 Lindeberg[7,8]在一系列合理的假設下得出,高斯卷積核是實現尺度變換的唯一可能的線性核。
尺度空間是SIFT進行極值點檢測的理論基礎,尺度空間的建立就是將一幅遙感影像 與不同尺度的高斯核 進行卷積,得出的一系列影像,即:
其中G(x,y,σ)是高斯函數,σ即為尺度空間因子。
由于高斯差分函數DoG具有效率高,易計算及穩定性強等特點,故SIFT采用DoG檢測關鍵點的位置,高斯差分函數如下:
2)將2τ+1個sigma點(χk|k)r(χk|k的第r列,r∈[1,2τ])依次代入永磁轉子離散狀態方程(6),計算采樣點集χk|k的預測值χk+1|k=f(χk|k)。
在DoG影像中,以3×3大小的窗口遍歷整幅影像,比較窗口中心點與鄰點已經其相鄰尺度層影像中對應的區域像素點的大小。因DoG算子具有較強的邊緣效應,所以為了獲得穩定且抗噪的特征點,必須去除低對比度與不穩定的邊緣點。檢測出的極值點利用擬合三維二次函數以子像素精度,來確定關鍵點的精確位置。
2.2.2 SIFT特征點描述
通過SIFT檢測子得到穩定的特征點,已經包含了尺度和位置信息,接下來對特征點進行方向描述。SIFT特征點最關鍵的特性是旋轉不變性,為了保持這個特性,需要對特征點賦予一個主方向,即對SIFT特征點與各相鄰像素點間的梯度大小及方向進行統計。以特征點為中心,在其鄰域內選取一個8×8的像素矩陣,再將此矩陣分割成16個2×2的子區域,分別計算每個子區域在8個方向上的梯度值,這樣就構成了一個8維向量。每個子區域包含一個8維向量,那么一個特征點就形成了8×16即128維向量,該特征向量即為SIFT特征點的描述子。最后,除了要保持關鍵點的旋轉不變性,描述子還需要對仿射變換和光照變化具有一定程度的魯棒性,因此還需將特征點的描述子進行歸一化。
2.3 SURF算法
SURF算法繼承了SIFT算法的匹配思想,將DoH中的高斯二階微分模板進行了近似簡化,并引入了積分圖像的概念,這使SURF算法在特征提取和特征描述的計算時間上顯示出優勢。Koendetink等對SURF算法和SIFT算法進行了實驗,結果表明在匹配速度方面,SURF算法約比SIFT算法節約了3倍的時間,綜合性能優于 SIFT 算法[9]。
2.3.1 SURF特征提取
SURF算法的尺度空間建立與SIFT不同,是利用積分圖像與高斯模板的近似盒子濾波器(Box-fliter)進行卷積,Box-fliter的構造如圖1所示。
SURF算法能夠于眾匹配算法中脫穎而出,還因為它將Hessian矩陣引入到匹配算法中。
假設像素點P(x,y)為圖像I上的任意一點,則該點在尺度為σ的高斯空間中的Hessian矩陣可表示為:
其中,Lxx(x,y,σ)表示高斯二階偏導在P處于圖像I的卷積,Lxy(x,y,σ)和Lyy(x,y,σ)可類推。
用Dxx,Dxy,Dyy替換 Hessian矩陣中的Lxx,Lxy和Lyy來表示盒子濾波模板和影像卷積計算的協方差,那么替換簡化后的Hessian矩陣行列式可用如公式(4)表示:
其中ω是權重系數。尺度空間構建完成后,利用特征監測算子Hessian矩陣對影像進行極值檢測,將檢測出的極值點與尺度空間中三層26個點進行比較,確定特征點,并根據閾值篩選適當的特征點。
2.3.2 SURF特征點描述
SURF算法是統計興趣點鄰域范圍內的灰度信息,同樣是計算主方向和特征向量來得到特征描述子。
SURF算法描述子的生成過程利用到了Haar小波模板。SURF算法特征描述子生成首先要以特征點為圓心,用Haar小波模板遍歷特征點的整個圓形鄰域,取最長向量和的方向作為主方向。
確定主方向后,對特征點進行描述。在生成描述子的過程中,同SIFT類似,以特征點為中心原點,旋轉坐標軸到該特征點的主方向,以σ作為采樣間隔,建立一個邊長為20σ的正方形窗口,將該正方形窗口進行分割,分成4×4的16個子窗口。再次利用Haar小波模板分別計算每個子窗口內的中心點水平于主方向的、垂直于主方向的Haar小波響應值,分別記為dx、dy。將子窗口內的dx和dy值在分別進行矢量和計算和絕對值之和的計算,便得到了每個子窗口的四維向量:v=(∑dx,∑dy,∑|dx|,∑|dy|)。
由此得出,一個特征點的正方形鄰域內包含了4×4個子窗口,特征點的描述符有著16個窗口的向量組成,便形成了一個4×4×4=64維的特征向量。
3 改進算法研究
在當前影像特征提取與匹配算法的研究過程中,依然存在許多問題有待解決。現有匹配算法中使用比較廣泛的是SIFT算法,然而其計算速度和對仿射不變特性都存在較大缺陷。SURF算法是近年來新提出的一種基于點特征的特征匹配方法,在重復度、獨特性、魯棒性這三個評價算法的標準上有著較為顯著的優勢,與以往提出的同類方法相比,均存在不同程度的超越,其匹配效果可與SIFT算法媲美,在計算效率上更是具有明顯的優勢。SURF算法繼承了SIFT算法的匹配思想,在保證了特征點提取質量的同時,在特征點提取的速度方面提出了改進,這使SURF算法在處理大量、實時的數據問題上更有應用價值。但SURF算法在影像仿射變換、旋轉角度等變形較大情況下對圖像特征點的提取和匹配效果依然不是很好。因此有人提出將MSER檢測算法引入SIFT和SURF中,分別與兩種方法結合,利用MSER本身的仿射不變特性,與SIFT和SURF兩種性能優異的匹配算法在空間分布上成互補關系[10]。
4 實驗結果與分析
本文對4種方法結合低空遙感影像分別進行了充分的實驗,采用的數據是某區域無人機影像,分辨率為0.2m。兩幅影像間存在仿射變化。下面對本組的兩幅影像進行4種方法的匹配實驗,實驗結果圖和實驗數據如圖2所示。
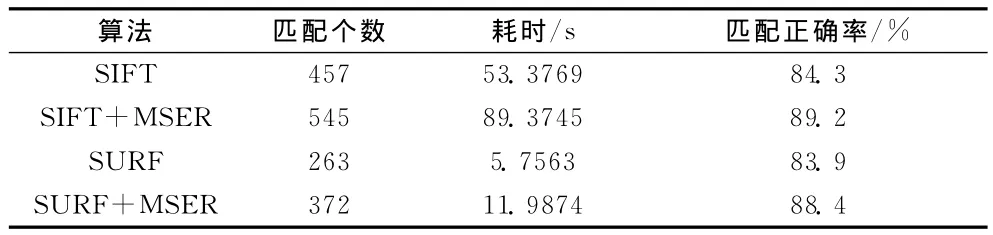
表1 四種算法匹配實驗數據
通過表1實驗數據可以得出,首先,無論是在特征點提取還是特征點描述方面,SURF+MSER算法和經典SURF算法在處理時間上是具有很明顯的優勢的,而包含了SIFT算法的兩種方法,在提取和描述特征點的時候,相對于其他兩種包含了SURF的算法來說計算所用的時間是相當多的。
然后,影像檢測出的特征點個數存在明顯差異,包含了SIFT算法的方法在提取到的特征點個數上遠遠超過了其他兩種算法,并且MSER+SURF檢測出的特征點的個數也比經典SURF算法明顯增加。
最后,在匹配正確率方面,經典SIFT算法和經典SURF算法的實驗結果相差不多,而結合MSER后的兩種算法匹配正確率也有了較為明顯的提升。
綜上,SURF+MSER算法和經典SURF算法在計算時間上與包含了SIFT算法的兩種方法相比縮短很多,這說明SURF+MSER算法充分吸收了SURF算法計算速度快的優勢的同時在特征點檢測的個數上比經典SURF算法的檢測能力有所提升,充分利用了MSER和SURF算法各自的優勢,彌補了SURF算法提取特征的不充足性。
5 結語
本文通過實驗數據充分驗證了SURF算法的改進算法相對于其他三種方法的綜合優勢,既可以在時間上滿足數據量大的低空遙感影像,又能在匹配的個數上滿足遙感數據的處理需求,適用于環境監測過程中遙感影像生產過程。
[1]張永軍 .無人駕駛飛艇低空遙感影像的幾何處理[J].武漢大學學報:信息科學版,2009,34(3):284~288.
[2]Matas J,Chum O,Urban M,Pajdla T.Robust wide baseline stereo from maximally stable extremal regions[C].BMVC,2002:384~393.
[3]D.G.Lowe.Distinctive Image Features from Scale-Invariant Keypoint[J].Internation Journal of Computer Virsion,2004,60(2):91~110.
[4]D.G.Lowe.Object Recognition from Local Scale-Invariant Features[J].International Conference on Computer Vision,1999:1150~1157.
[5]H.Bay,T.Tuytelaars,L.V.Gool.SURF:Speeded up Robust Features[J].Computer Vision and Image Understanding,2006,110(3):346~359.
[6]Mikolajczyk K,Tuytelaars T,Schmid C,et al.A comparison of affine region detectors[J].International journal of computer vision,2005,65(1-2):43~72.
[7]Vincent L,Soille P.Watersheds in digital spaces:an efficient algorithm based on immersion simulations[J].IEEE transactions on pattern analysis and machine intelligence,1991,13(6):583~598.
[8]Lindeberg T.Scale-space for discrete Signals[J].IEEE Transactions PAMI,1980(207):187~217.
[9]Koendetink J.The structure of image[J].Biological Cybernetics,1984(50):363~369.
[10]唐 樂,路林吉 .基于 MSER與SURF的圖形匹配新方法[J].微型電腦應用,2012,28(3):61~64.

