基因識別的綜合優化算法及精確性分析

姜 林，劉湘偉

(電子工程學院，合肥 230037)

?

基因識別的綜合優化算法及精確性分析

姜 林，劉湘偉

(電子工程學院，合肥 230037)

針對現有算法難以精確地確定基因外顯子的2個端點，結合 “基于固定長度滑動窗口上頻譜曲線的基因識別方法”、“基于DNA序列上“移動序列“信噪比曲線的基因識別方法”、“小波算法”3種方法，采用綜合優化算法對基因進行識別，最后通過誤差評估驗證了算法的精確性。

綜合優化算法；基因識別；誤差評估；精確性

1 背景研究

對給定的DNA序列，如何識別出其中的編碼序列(即外顯子)也稱為基因預測，是一個尚未完全解決的問題，也是當前生物信息學的一個最基礎、最首要的問題。現在已經有一些研究者提出了識別基因的算法。目前利用信噪比的基因識別算法通常有2種：一種是固定長度窗口滑動法[1-2]；另一種是移動信噪比曲線識別法[3]。但由于DNA序列隨機噪聲的影響等原因，還很難“精確地”確定基因外顯子區間的2個端點。鑒于上述原因，本文以“基于固定長度滑動窗口上頻譜曲線的基因識別方法”和“基于DNA序列上“移動序列“信噪比曲線的基因識別方法”為基礎，進而可創造性地研究小波算法，嘗試解決DNA序列隨機噪聲的影響，可以比較精確地確定基因外顯子區間的2個端點，進而通過分析對比“基于固定長度滑動窗口上頻譜曲線的基因識別方法”、“基于DNA序列上“移動序列“信噪比曲線的基因識別方法”、“小波算法”和“綜合優化算法”，建立誤差評估函數，并運用圖表形象地展示評估算法的結果。

2 生物基因識別綜合優化算法的分析和研究

本文首先在“基于固定長度滑動窗口上頻譜曲線的基因識別方法”和“基于DNA序列上“移動序列“信噪比曲線的基因識別方法”,2種方法的基礎上，對算法結果的充分性和準確性進行了進一步的改進；進而創造性地將信號處理方面的小波算法運用到基因識別中，有效地去除了DNA序列中隨機噪聲的影響，比較精確地確定了基因外顯子區間的2個端點。下面以所查基因數據為例來說明此算法。

2.1 基于固定窗口滑動法得出外顯子大致區域

(1) 在參考文獻中有此種方法的闡述，對基于固定長度滑動窗口上頻譜曲線的基因識別方法的滑動進行MATLAB編寫程序，實現算法；

(2) 對窗口按照FFT算法進行快速傅里葉變換，進而求出基因的功率譜；

(3) 通過MATLAB程序中的循環語句，實現窗口自動移動，實現算法的軟件自動化；

(4) 對所研究的基因的功率譜進行歸一化處理；

(5) 運用MATLAB軟件作出基因的功率譜圖像(見圖1)。

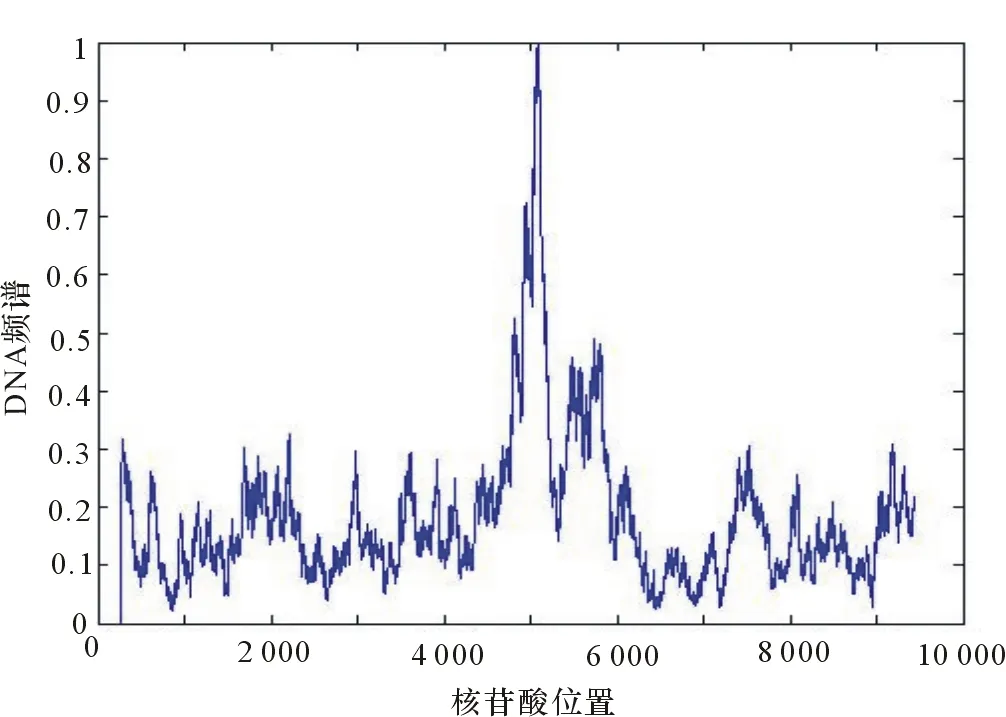
圖1 人類的基因序列的功率譜(1)

2.2 移動信噪比曲線法對區域進一步細化

(1) 對基于DNA序列上“移動序列”信噪比曲線的基因識別方法的移動進行MATLAB程序編寫，實現算法；

(2) 通過MATLAB程序中的循環語句，使區域進行步長為3的變化，實現算法的軟件自動化；

(3) 對所研究的基因序列區域進行快速傅里葉變換(FFT)，得到基因序列的功率譜圖像(見圖2)。

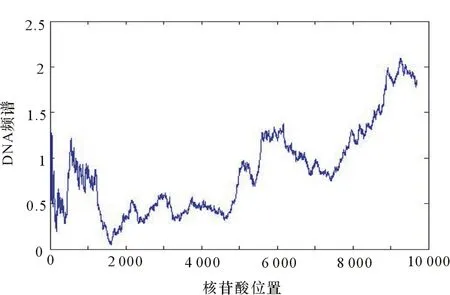
圖2 人類的基因序列的功率譜(2)

因為DNA序列的信噪比移動曲線的峰、谷與基因外顯子區間的端點也具有較“明顯的”的對應關系。所以運用基于DNA序列上“移動序列”信噪比曲線的基因識別方法，可以對區域進一步精化，從而使區域范圍更加準確，得出外顯子的大致范圍為：(4 554，5 109)，(5 256，5 583)，(7 419，7 974)。

2.3 小波算法的精確化處理

小波分解是時間和頻率的局域變換，因而能有效地從信號中提取信息，通過伸縮和平移等運算功能對信號進行多尺度分析。實際中使用的是離散小波變換、工程上常用二進制小波變換。與標準傅里葉變換相比, 小波分析中所用到的小波函數具有不唯一性，即小波函數具有多樣性。目前主要是通過用小波分析方法處理信號的結果與理論結果的誤差來判定小波基的好壞，并由此選定小波基。

(1) 小波理論簡介

設x(t)是平方可積函數,ψ(t)是基本小波或母小波(MW)函數,且滿足容許條件：

(1)

則：

(2)

式中：ωx(a,b)為x(t)的小波變換式；b為位移，其值可正可負；上標*代表共扼。

這就稱為x(t)的小波變換。

如果x(t)為信號函數，則小波變換是信號與小波函數的內積，是對信號滿足一定附加條件的濾波，這種附加條件反映在小波函數及小波因子選擇上。高頻時使用小尺度a值，時軸上觀察范圍小，而頻域上相當于用高頻小波作細致觀察；低頻時使用大尺度a，時軸上考察范圍大，而頻域上相當于用低頻小波作概貌觀察[4]。利用小波變換所具有的這種數學顯微鏡特點和頻域帶通特性，把所有的信號分離出來，再進行分析研究。

(2) 基因小波變換模型的建立

在實際運用中，尤其在計算機實現時，一般采用離散小波變換。最常用的是二進小波變換，b=k×2-j，a=2-j，j,k∈Z，其小波序列為：

(3)

對任意平方可積函數y(t)來說，其離散小波變換(DWT)為：

(4)

對任意y(t)∈Vj，若yk為信號的離散采樣數據，令cj,k=yk(應用中常以c0,k=yk作為計算的初始信號序列)，則有信號的多分辨率分析公式為：

(5)

(6)

式中：cj,k為信號的逼近信號；dj,k為信號的細節。

相應地，有基因小波變換模型為：

(7)

可見，一個信號可以由小波進行系數重構。本文使用小波算法進行信號重構，以消除DNA序列隨機噪聲的影響，較精確地確定了基因外顯子區間的2個端點。

(3) 利用基因小波變換模型進行基因識別(如圖3)

圖3 小波基因識別流程

對DNA序列數值化映射后得到{uA[n]}、{uG[n]}、{uC[n]}、{uT[n]}，使用MATLABTOOLBOXES中的WAVELET，對數據進行相關的小波變換處理，并與FFT結果比較，得到外顯子的相應區間：(4 562，5 047)，(5 253，5 427)，(7 445，7 983)。

3 生物基因識別算法的精確性分析

在基因的識別算法中可能存在一定的誤差，為此對上述建立的基因識別綜合算法模型進行了逐步深入的研究，并建立誤差評估函數，用數據形象證明了算法逐步優化的過程，最終確定算法的高效性。

3.1 基因識別算法的誤差評估函數

誤差評估函數如下：

；i=0,1,2

(8)

所得到的函數值hi越大，表明在確定外顯子區域時的誤差越大。

對于一段DNA序列，可能有N段外顯子，則對于這段DNA序列來講，對外顯子的識別誤差為：

(9)

3.2 精確性分析

(1) 在所查數據中可以得到人類基因序列中外顯子的準確位置：(4 577，4 996)，(5 251，5 398)，(7 458，7 996)。

(2) 對單獨使用“基于固定長度滑動窗口上頻譜曲線的基因識別方法”、 “基于DNA序列上“移動序列“信噪比曲線的基因識別方法”、“小波算法”對外顯子的識別與使用“綜合優化算法”的結果比較，得到數據如表1所示。

表1 4種算法對外顯子識別結果與準確值的對比

表1中，算法1為“基于固定長度滑動窗口上頻譜曲線的基因識別方法”；算法2為“基于DNA序列上“移動序列“信噪比曲線的基因識別方法”；算法3為“小波算法”；算法4為“綜合優化算法”。

(3) 運用誤差評估函數得到每種算法對單個外顯子以及整個DNA序列的誤差如表2所示。

表2 誤差評估分析表

4 結束語

(1) 數值越大，說明該種算法的誤差越大。

(2) 從表中可以看出，對每一列進行對比時，通過新算法的逐步優化，得到的結果也層層推進，逐步接近正確值，誤差越來越小，說明精確度越來越高，通過新算法可以使誤差保持在0.1 左右。

(3) 對每一行進行對比時，發現區域越小(尤其100左右時)，誤差越大，說明僅通過信噪比對區域過小的外顯子序列進行區分是不精確的。

[1] 王玉.基于傅里葉技術快速預測DNA序列編碼區[J].電子科技大學學報,2006,35(5):837-840.

[2]BerrymanMJ,AlisonA.Reviewofsignalprocessingingenetics[J].FluctuationandNoiseLetters,2005,5(4):13-35.

[3]YinC,YauS.Predictionofproteincodingregionsbythe3-baseperiodicityanalysisofaDNAsequence[J].JournalofTheoreticalBiology，2007，2(47):687-694.

[4] 王正林.精通MATLAB[M].北京：電子工業出版社,2009.

Analysis of Integrated Optimized Algorithm and Accuracy of Gene Identification

JIANG Lin,LIU Xiang-wei

(Electronic Engineering Institute，Hefei 230037，China)

Because existing algorithms can not accurately judge the two points of expressed region of gene,this paper combines three methods:gene identification method based on spectrum curve of slip window with fixed length,gene identification method based on mobile sequence signal-to-noise ratio (SNR) curve of DNA sequence,wavelet algorithm,uses integrated optimized algorithm to identify the gene,finally validates the accuracy of the algorithm through error estimation.

integrated optimized algorithm;gene identification;error estimation;accuracy

2014-09-09

TP391.9

A

CN32-1413(2015)01-0080-04

10.16426/j.cnki.jcdzdk.2015.01.019