任意齒差滾動活齒傳動壓力角計算方法及其影響因素分析*

宜亞麗 劉朋朋 金賀榮

(燕山大學機械工程學院，河北 秦皇島 066004)

滾動活齒傳動具有結構緊湊、傳動比大、承載能力強和傳動效率高等特點，在航空航天、數控機床、醫療器械等領域具有良好的應用前景［1］。一齒差滾動活齒傳動通常采用偏心圓激波器，需進行動平衡處理。李瑰賢等［2］建立了偏心圓滾動活齒傳動的力學模型，推導了滾柱活齒傳動機構各構件的受力計算公式;Krylov N.V.［3］對偏心圓滾動活齒傳動進行強度分析，得到了應力和應變的分布情況。

多齒差滾動活齒傳動裝置為幾何軸對稱結構，在傳動過程中易實現整機靜、動態受力自平衡，避免傳動系統的振動激勵，成為活齒傳動領域的研究熱點。董新蕊等［4］提出凸輪激波復式滾動活齒傳動裝置，對其傳動原理、傳動比及傳動特性進行了分析;MIZUKAMI等［5-6］提出了一種活動銷輸入型擺線凸輪多齒差滾動活齒傳動機構;梁尚明等［7］將優化設計理論與穩健設計方法相結合，建立了二齒差滾動活齒傳動的多目標穩健優化設計數學模型;黃勁枝等［8］對激波器和中心輪齒廓均采用余弦類曲線的任意齒差數純滾動活齒傳動進行了研究。宜亞麗等［9］采用無剛性、柔性沖擊的5 次多項式類曲線的齒形模型，實現了滾動活齒任意齒差等速共軛傳動。

壓力角作為衡量活齒機構傳動性能的重要參數，其大小影響著機構的受力狀況、傳動效率及工作可靠性，研究壓力角變化規律及其影響因素對于指導活齒傳動設計具有重要意義。本文建立多類齒形統一齒廓方程，推導出滾動活齒傳動機構壓力角解析式，分析不同齒形滾動活齒傳動機構壓力角的變化規律，確定壓力角的影響因素。

1 滾動活齒傳動原理

如圖1 所示，滾動活齒傳動由激波器、活齒、活齒架和中心輪組成，激波器和中心輪齒廓曲線按照給定的運動規律和傳動比確定，其中活齒由活齒軸和滾動軸承組成，通過滾動軸承使組成高副的兩運動副元素間形成局部自由度，實現激波器齒廓、中心輪齒廓、活齒槽與活齒的純滾動接觸嚙合。Ⅰ類傳動形式為活齒架固定，激波器輸入，中心輪輸出。激波器勻速旋轉時，活齒中心始終處于激波器理論廓線與中心輪理論廓線交點位置處并沿活齒架的活齒槽作徑向運動，推動中心輪轉動輸出。Ⅱ類傳動形式為中心輪固定，激波器輸入，活齒架輸出。

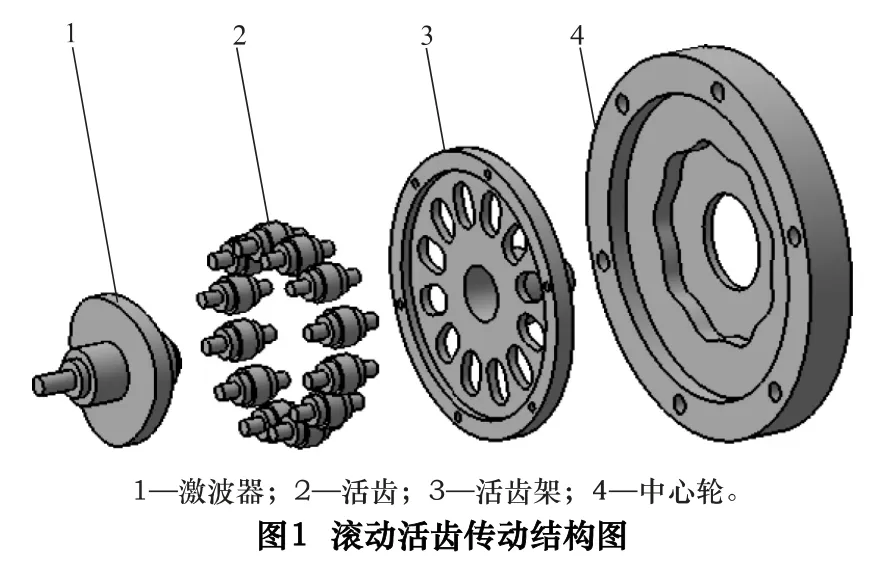
2 齒廓方程建立

選定活齒運動規律即可設計出滿足要求的激波器齒廓和中心輪齒廓，常用的活齒運動規律有偏心圓類曲線、橢圓類曲線、余弦類曲線和高次多項式類曲線等。文中各符號含義如表1 所示。

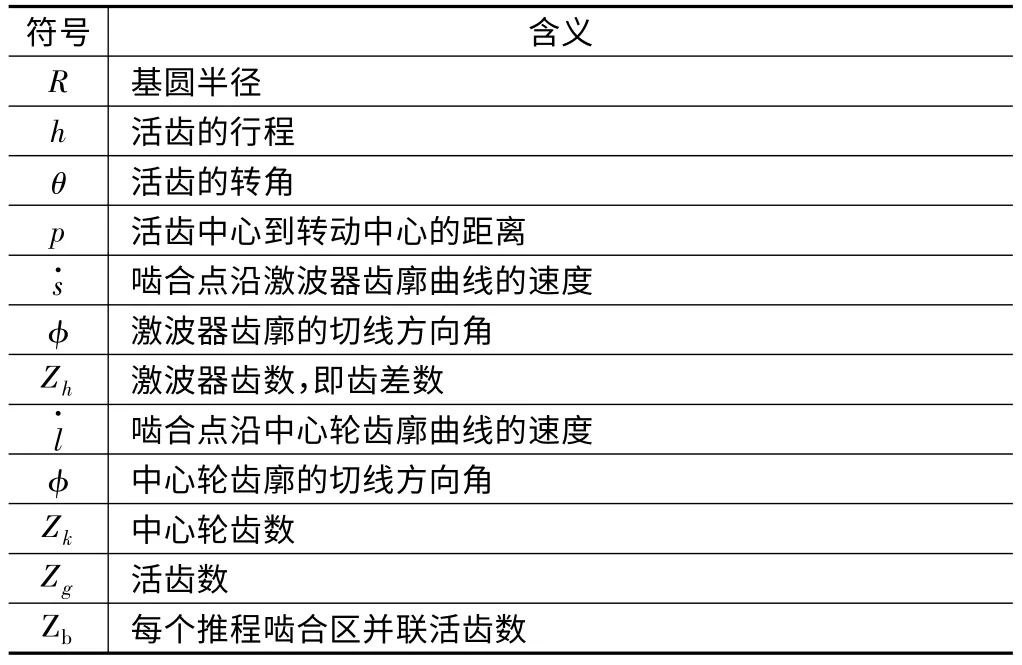
表1 滾動活齒傳動各符號含義

2.1 活齒的運動規律

圖2 為偏心圓激波器齒形，由余弦定理知

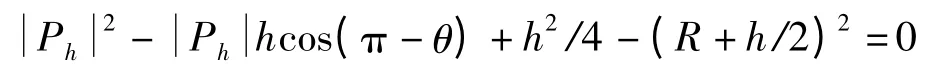
于是可得

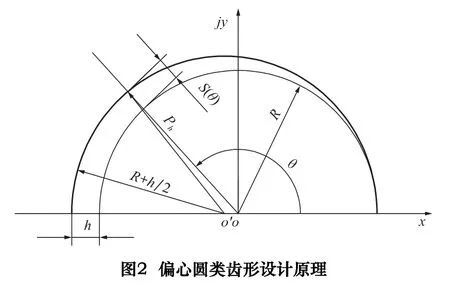
偏心圓類齒形活齒運動規律為

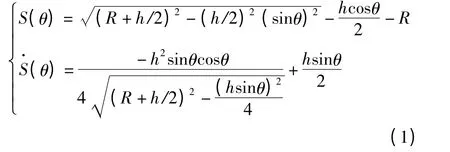
圖3 為橢圓激波器齒形，由橢圓參數方程知

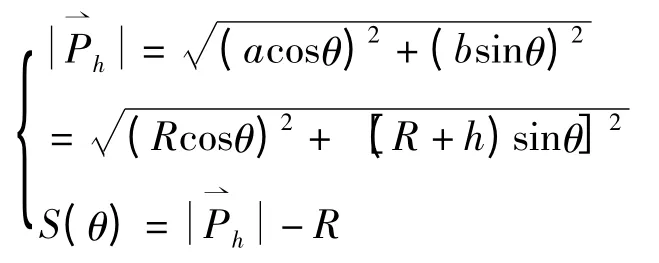
橢圓類齒形活齒運動規律為

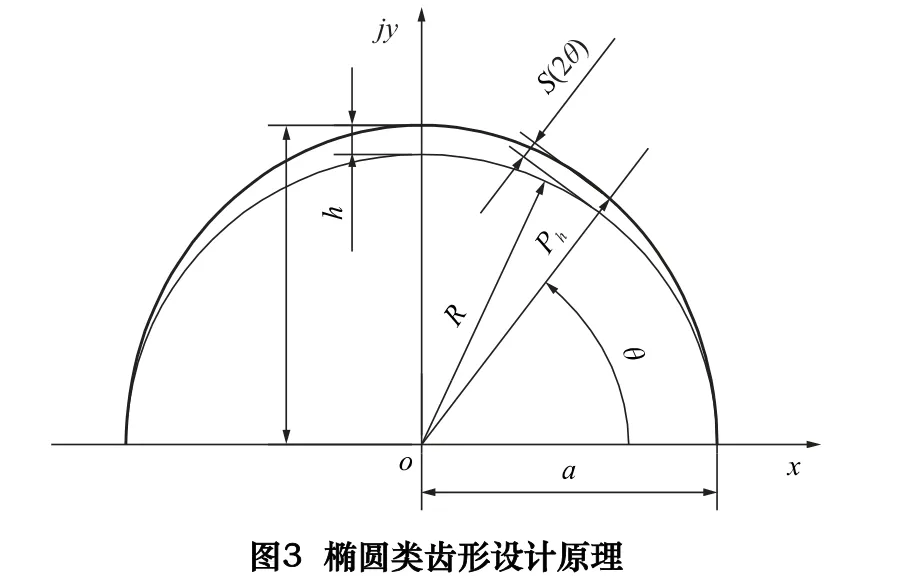
式中:a 為橢圓短半軸;b 為橢圓長半軸;h=b -a;R=a。

如圖4 所示，余弦類齒形活齒運動規律為

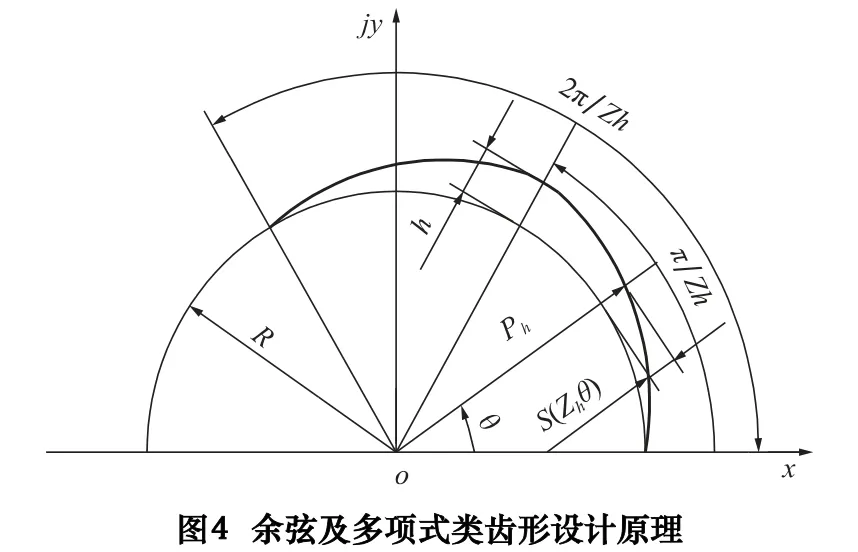
高次多項式類齒形活齒推程運動規律為

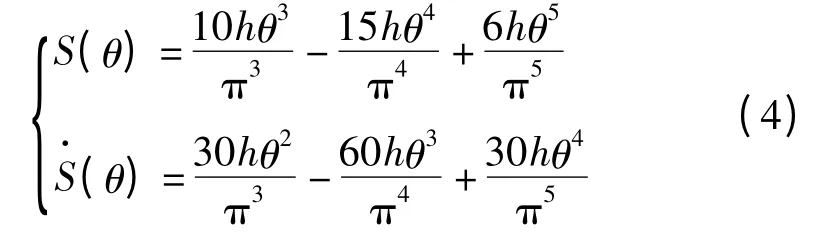
回程運動規律為

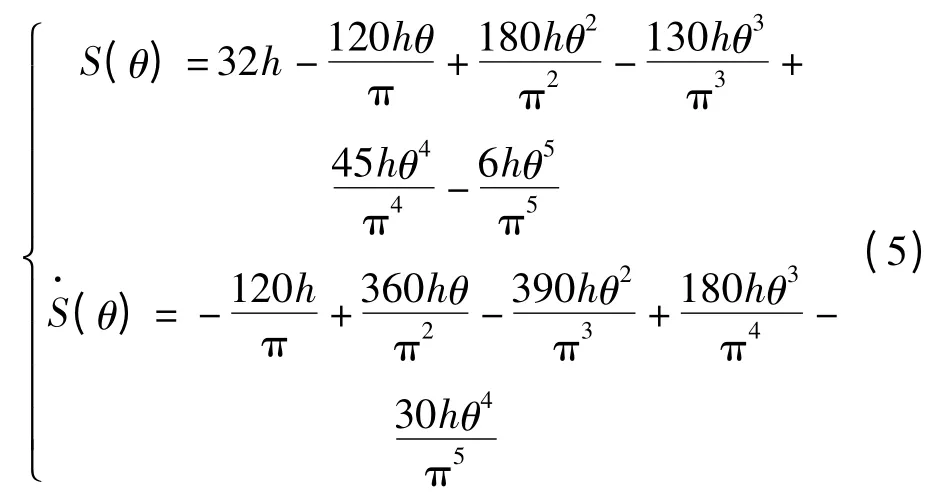
2.2 齒廓方程

圖2～4 中θ∈［0，π/Zh］為活齒的推程，θ∈［π/Zh，2π/Zh］為活齒的回程。不同齒形激波器理論廓線方程統一為

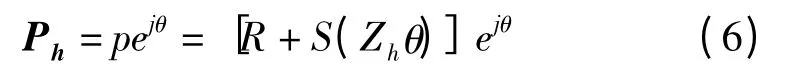
其展開式為

對向量Ph求導得

不同齒形中心輪理論廓線方程統一為

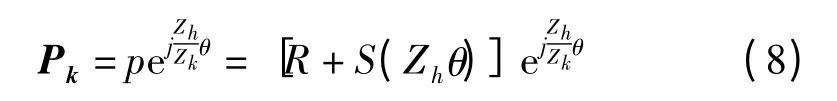
其展開式為

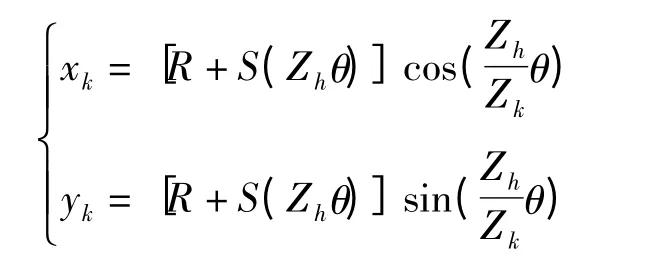
對向量Pk求導得

3 機構壓力角解析

在傳動機構運轉過程中，影響機械動力特性的一個主要因素是齒廓曲線接觸點處的壓力角，即接觸點處所受的法向力(與齒廓對應點的公法線方向一致)與該點速度方向所夾的銳角［10］。

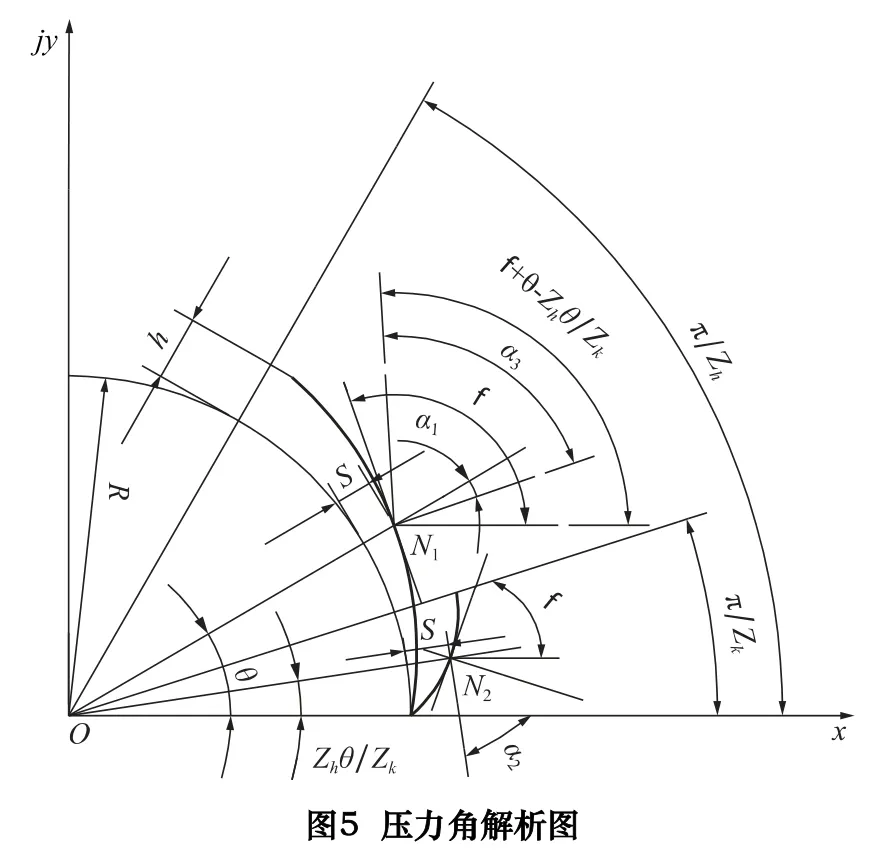
如圖5 所示，Ⅰ類傳動形式中，激波器與活齒間嚙合壓力角α1為激波器對活齒法向作用力方向與活齒運動方向間所夾銳角;活齒與中心輪間壓力角α2為活齒對中心輪法向作用力方向與中心輪運動方向間所夾銳角。

Ⅱ類傳動形式中，激波器與活齒間壓力角α3為激波器對活齒法向作用力方向與活齒運動方向間所夾銳角;活齒與活齒架間壓力角α4為活齒對活齒架法向作用力方向與活齒架運動方向間所夾銳角，大小始終為零。

激波器與活齒間嚙合壓力角α1為

活齒與中心輪間的嚙合壓力角α2為

激波器與活齒間嚙合壓力角α3為

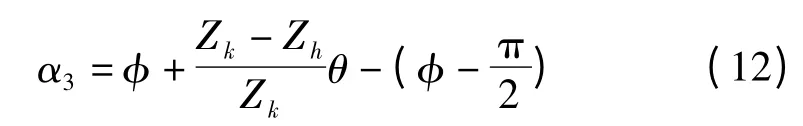
活齒與活齒架間的嚙合壓力角α4

由式(7)和式(9)可得滾動活齒傳動激波器、中心輪齒廓的切線方向角分別為

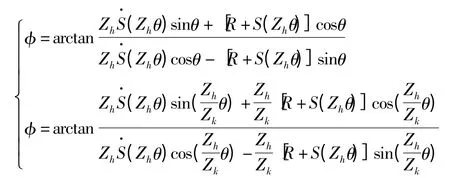
由反正切函數值域知，φ∈(-π/2，π/2)，第一象限內，當φ∈(-π/2，0)時，在arctan 的主值上加π;第二象限內，當φ∈(0，π/2)時，在arctan 的主值上加π。

4 仿真與分析

滾動活齒傳動齒形參數如表2 所示，根據表2 中數據進行實例仿真。

表2 滾動活齒傳動齒形參數

活齒傳動是多齒嚙合傳動，一、二、三齒差活齒傳動的一個推程嚙合周期分別為180°、90°和60°。根據表2 參數，以一齒差偏心圓類為例，繪制一個推程嚙合區4 個并聯活齒的壓力角α1、α2、α3的示意圖，4 個并聯活齒編號依次為①、②、③、④，嚙合相位差為45°，如圖6 所示。同理，二齒差橢圓類一個推程嚙合區有4 個并聯活齒，4 個并聯活齒編號依次為①、②、③、④，嚙合活齒的相位差為22.5°;三齒差余弦類和多項式類一個推程嚙合區有3 個并聯活齒，3 個并聯活齒編號依次為①、②、③，嚙合活齒的相位差為20°。多活齒并聯嚙合協同工作，重合度高，使活齒傳動具有較強的承載力和抗沖擊載荷的能力，傳動平穩、噪聲小。

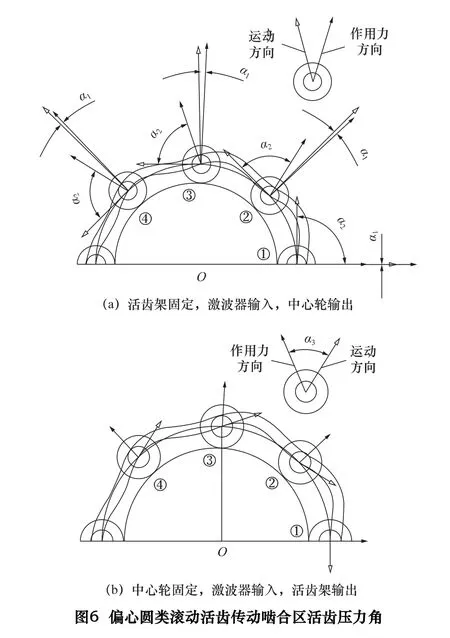
4.1 Ⅰ類傳動形式

Ⅰ類傳動形式中激波器與活齒間的嚙合壓力角α1的變化曲線如圖7 所示。

隨著激波器轉動，α1不斷變化且變化平緩，開始從0°變化到最大值α1max，然后又從最大值α1max變化到0°，在推程的起點和終點壓力角α1為0°，顯然最大值α1max越小，對傳動越有利。一齒差偏心圓類α1max=2.7°最小，其次是二齒差橢圓類α1max=5.5°，三齒差余弦類α1max=8.5°和三齒差多項式類α1max=9.7°，相對于一、二齒差滾動活齒傳動較大些，但最大值α1max仍然較小，保證激波器與活齒間嚙合傳力性能。

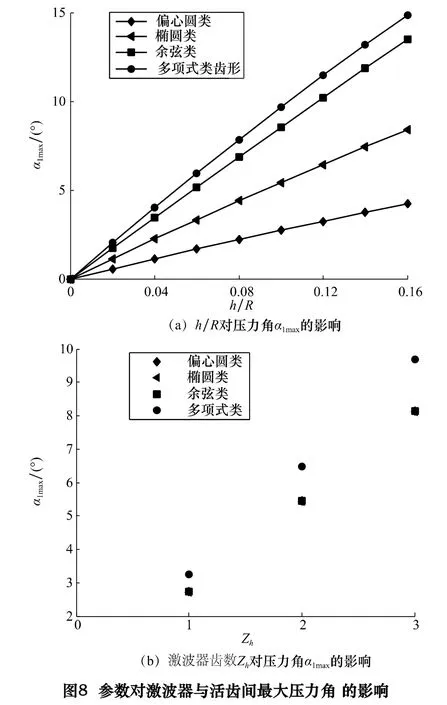
由式(10)知α1max與齒形參數R、h 和Zh有關。改變h/R，保持其他參數不變，可得壓力角α1max隨h/R的變化曲線，如圖8a 所示，壓力角α1max隨基圓半徑R的增大而減小，隨行程h 的增大而增大，α1max與h/R 成線性關系，隨h/R 的增大而增大;改變激波器齒數Zh，保持其他參數不變，可得壓力角α1max隨激波器齒數Zh的變化曲線，如圖8b 所示，壓力角α1max與激波器齒數Zh基本成線性關系，隨激波器齒數Zh的增大而增大。

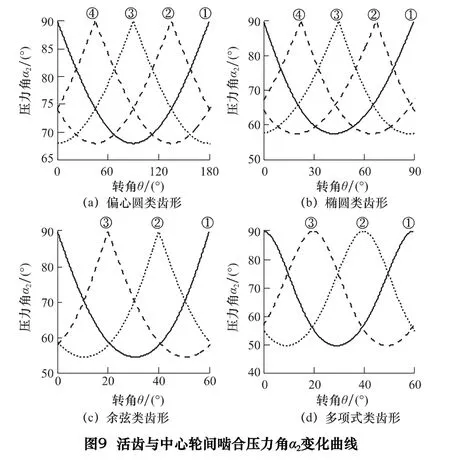
活齒與中心輪間的嚙合壓力角α2的變化曲線如圖9 所示。隨激波器轉動，α2不斷變化且變化平緩，開始從90°變化到最小值，然后又從最小值變化到90°，在推程的起點和終點壓力角為90°，最小值α2min越小，對傳動越有利。一齒差偏心圓類活齒傳動α2min=68.0°，二齒差橢圓類活齒傳動α2min=57.5°，三齒差余弦類活齒傳動α2min=54.4°，三齒差多項式類活齒傳動α2min=50.0°。滾動活齒傳動是多齒嚙合傳動且壓力角α2變化存在相位差，活齒與中心輪間的壓力角α2可滿足傳動要求。

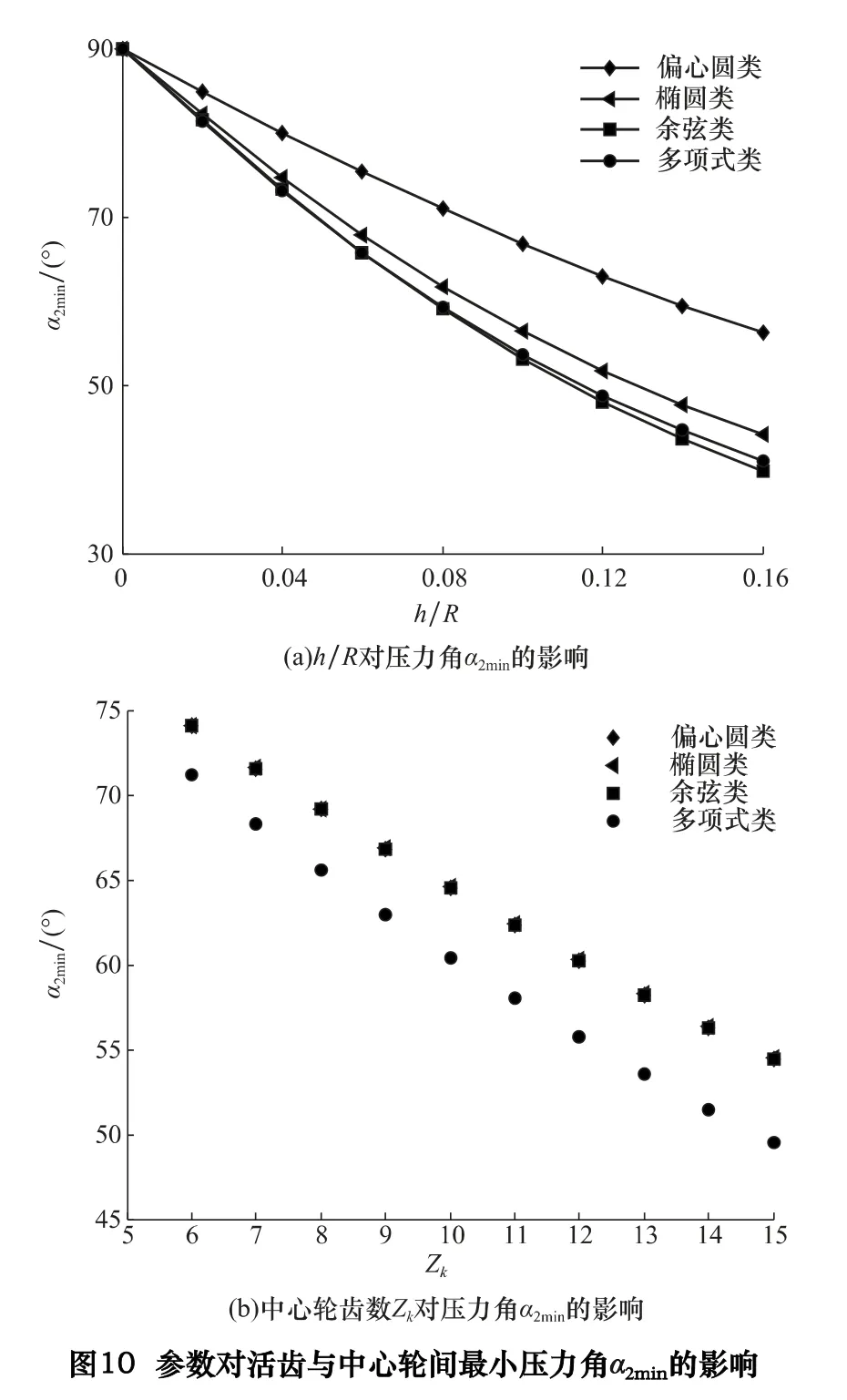
改變h/R，保持其他參數不變，可得壓力角α2min隨h/R 的變化曲線，如圖10a 所示，壓力角α2min隨基圓半徑R 的增大而增大，隨行程h 的增大而減小，α2min與h/R 近似成線性關系，隨h/R 的增大而減小。

改變激波器齒數Zk，保持其他參數不變，壓力角α2min隨中心輪齒數Zk的變化曲線如圖10b 所示，壓力角α2min與中心輪齒數Zk基本成線性關系，隨中心輪齒數Zk的增大而減小。顯然，參數對α1max和α2min的影響恰好相反，無法同時獲得最小的α1max和α2min。當活齒架固定，激波器輸入，中心輪輸出時，考慮到α1在0°到α1max之間變化且值較小，α2在α2min和90°之間變化且值較大，所以選擇齒形參數時，應主要考慮參數對中心輪與活齒間最小壓力角α2min的影響。

4.2 Ⅱ類傳動形式

Ⅱ類傳動形式中激波器與活齒間的嚙合壓力角α3的變化曲線如圖11 所示。隨激波器轉動，α3不斷變化且變化平緩，開始從90°變化到最小值α3min，然后又從最小值α3min變化到90°，在推程的起點和終點壓力角為90°，最小值α3min越小，對傳動越有利。一齒差偏心圓類α3min=69.5°最大，其次是二齒差橢圓類α3min=61.5°和三齒差余弦類α3min=62.5°，三齒差多項式類α3min=59.0°，相對于其他類滾動活齒傳動較小些，激波器與活齒間傳力性能較好。多活齒嚙合存在相位差，并聯協同工作可滿足傳動要求。

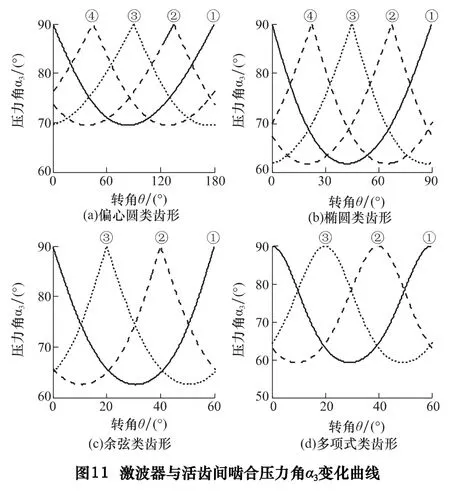
由于活齒與活齒架間壓力角α4隨激波器的轉動保持不變且時刻為零，當中心輪固定，激波器輸入，活齒架輸出時，選擇齒形參數只需考慮參數對激波器與活齒間最小壓力角α3min的影響。

改變h/R，保持其他參數不變，可得壓力角α3min隨h/R 的變化曲線如圖12a 所示，壓力角α3min隨基圓半徑R 的增大而增大，隨行程h 的增大而減小，α3min與h/R 近似成線性關系，隨h/R 的增大而減小;改變激波器齒數Zh，保持其他參數不變，可得壓力角α3min隨激波器齒數Zh的變化曲線如圖12b 所示，壓力角α3min與激波器齒數Zh基本成線性關系，隨激波器齒數Zh的增大而增大;壓力角α3min隨中心輪齒數Zk的變化曲線如圖12c 所示，壓力角α3min與中心輪齒數Zk基本成線性關系，隨中心輪齒數Zk的增大而減小。

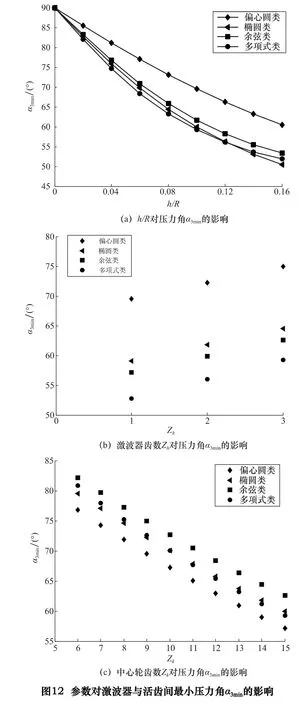
5 結語

(1)活齒嚙合壓力角α1、α2、α3的大小都隨活齒轉角的變化而變化，不同時刻壓力角不同且壓力角的極值一般發生在嚙合過程的中點;活齒壓力角α4不隨活齒轉角的變化而變化，且時刻為零。

(2)基圓半徑R、行程h、激波器齒數Zh和中心輪齒數Zk都會影響活齒機構壓力角的大小，不同活齒傳動齒形下，機構壓力角的變化規律不同，但變化趨勢相同。壓力角α1max隨h/R 的增大而增大，隨Zh的增大而增大;壓力角α2min和α3min隨h/R 的增大而減小，隨Zk的增大而減小;壓力角α3min隨Zh的增大而增大。

(3)建立不同類型齒形廓線方程的統一數學表達式，有助于針對活齒運動規律不同的任意齒差滾動活齒機構開展功能和性能的后續研究工作。

［1］曲繼方.活齒傳動理論［M］.北京:機械工業出版社，1993.

［2］李瑰賢，楊偉君，顧曉華.滾柱活齒傳動受力分析的研究［J］.機械設計，2002，19(1):18 -20.

［3］Krylov NV.Strength analysis of wave gear with intermediate rolling bodies with rotational motion of the output link［J］.Trudy MAI，2013，65:1 -15.

［4］董新蕊，李劍鋒，王新華，等.凸輪激波復式活齒傳動的結構及齒形分析［J］.中國機械工程，2006，17(16):1661 -1665.

［5］Masami Mizukami，Hidetsugu Terada.Study on movable pins input type trochoid gear reducer(1st Report)［J］.Japan Society for Precision Engineering，2009，75(11):1335 -1339.

［6］Masami Mizukam，Hidetsugu Terada.Study on movable pins input type trochoid gear reducer(2st Report)［J］.Japan Society for Precision Engineering，2010，76(6):663 -667.

［7］梁尚明，孫強，姚進.二齒差滾動活齒傳動多目標穩健優化設計［J］.西南交通大學學報，2012，47(2):241 -244.

［8］黃勁枝，程時甘，陳賢湘.任意齒差數純滾動活齒傳動［J］.機械設計與研究，2008，24(4):44 -46.

［9］宜亞麗，劉朋朋，安子軍，等.任意齒差推桿活齒高次多項式曲線齒廓齒形研究［J］.機械傳動，2014，38(4):1 -4.

［10］楊瑋，曹巨江.弧面凸輪機構的壓力角和曲率分析［J］.機械科學與技術，2004，23(1):74 -76.