常規混合流水車間調度問題的等價變換

蘇志雄，伊俊敏

SU Zhi-xiong, YI Jun-min

（廈門理工學院 管理學院，廈門 361024）

0 引言

混合流水車間（Hybrid Flow Shop, HFS）調度問題是在流水車間（Flow Shop, FS）調度問題的基礎上發展起來的，其特點是所有階段或部分階段上存在并行設備。常規HFS調度問題可以描述為n個工件要在s 個階段的流水車間上加工，其中階段k具有M(k)個同速平行機、且至少有一個階段存在兩臺以上的平行機，在滿足一系列基本假設和約束條件的基礎上去尋找一個調度解使得最大完工時間（makespan）最小。雖然不同的HFS問題不能完全滿足常規問題的所有假設和約束，但是也只是在設備加工環境、加工約束和特征、優化準則等方面存在較小的差異。常規HFS問題作為HFS調度問題的“模板”，其研究成果可以為更加復雜的實際調度問題研究提供基礎，受到了學術界和產業界的廣泛關注。

由于常規HFS調度問題的NP難特性[1]，精確算法[2,3]只能求解很小規模的問題。對于近似求解方法來說，啟發式算法[4,5]求解快速，然而其求解質量還有較大的改進空間；元啟發式算法[6～10]求解質量較高，通常需要更多的計算資源，難以應用于大規模或者實時性要求高的問題。從已有研究來看，現有的調度算法在求解質量、求解效率方面仍存在一定的不足，其主要原因在于算法設計的理論基礎不夠完善，現有的調度算法尚未很好地融入領域知識（domain knowledge）。此外，文獻[7]試圖通過反例來說明常規HFS問題不具備加工可逆性：對于一個給定的工件排列次序（初始階段），采用正序、逆序調度方法可以獲得不同的makespan值；然而在給定工件排列次序的情況下，可以生成不同的工件設備指派方案，進而可以得到一系列不同的調度解，該結論并不嚴謹。因此，本文進一步對常規HFS調度問題的本質特征展開研究，首先通過逆序變換定義了常規HFS調度問題的逆序問題，然后從數學角度證明了兩者之間的等價關系，最后給出了一種基于逆序變換進行問題求解的方法，旨在為后續的研究提供理論依據。

1 數學模型

1.1 符號定義

為了敘述方便，引入下列符號：

m為設備編號；

M(k)為階段k上的平行機數；

(j,k)為工件j在第k個階段的操作；

pjk為工件j在階段k的加工時間；

tjk,cjk為工件j在階段k的開工時間、完工時間；

Nkm為階段k上的設備m所加工的操作集合；

?k為階段k上的工件設備指派方案集合，集合的元滿足以下兩個條件：

Π 為對于給定的工件設備指派方案ω，可行的工件加工順序方案集合；

S為可行調度解，其集合記為Ψ，不妨記其最大完工時間記為Cmax(S)。

1.2 析取圖模型

對于給定的工件設備指派方案ω，常規HFS調度問題可以用賦權析取圖來表示：是節點集，其中節點(j,k)表示工件j在第k個階段的操作，而“0”與“*”分別表示整個加工開始的起點和代表全部加工結束的終點；A是合取弧的集合，反映了同一工件的不同操作之間的先后關系，用單向實線來表示；E是析取弧的集合，反映了同一設備上不同工件之間的加工先后關系，同一階段的任意兩個工件之間用雙向虛線來連接；w 是有向圖的權重，其中節點(j,k)的權重為pjk，而節點“0”、“*”和所有弧的權重都為0。

在上述描述中，調度的過程就是將雙向箭頭用單向箭頭代替進而得到E′，使G成為一個無回路的單向圖亦即確定了一個可行的工件加工順序方案，該圖可以簡記為在滿足時序約束、資源約束等的基礎上，確定工件的開工時間，進而生成一個可行調度解S。例如，對于一個7個工件3個階段的常規HFS調度問題，各階段上的平行機數分別為2、2、3；已知工件的加工順序方案，其中11=(1,2,3)，那么對應的如圖1所示。由于的關鍵路徑長度就是對應工件加工順序方案的最優makespan值，因此在所有的中尋找一個具有最小關鍵路徑的無回路單向圖就是常規HFS調度問題，即

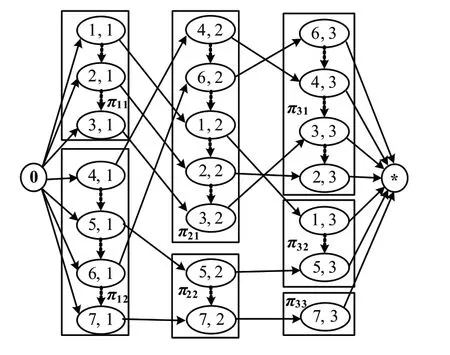
圖1 實例的圖表示

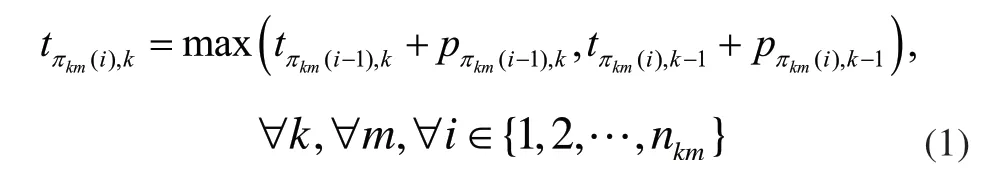
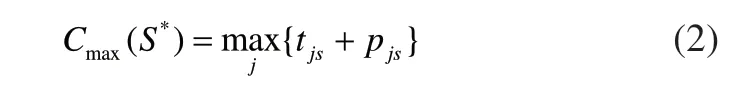
2 等價逆序變換

定義1：對于一個給定的具有n個工件的常規HFS調度問題，如果另外一個常規HFS問題滿足以下兩個條件：

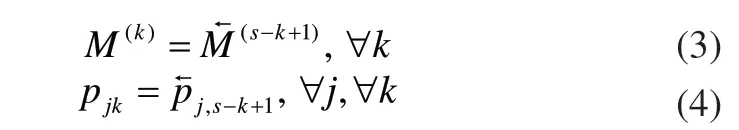
對于任意的常規HFS調度問題（原問題），可以根據定義1的逆序變換得到相應的逆序問題。為了證明逆序變換的等價性，下面給出了優化問題的等價性定義。

定義2：如果兩個優化問題滿足：1）存在一個問題的可行解集合到另外一個問題的可行解集合的映射（不一定是“一對一”的情形）；2）任意一個可行解及其“像”具有相同的目標函數值；那么這兩個優化問題是等價的。

引理1：對于原問題的任意一個可行調度解S，記其工件加工順序方案為，那么至少存在逆序問題的一個可行調度解，其工件加工順序方案構造如下：階段上的設備m 所加工的工件有序集為且這兩個調度解具有相同的makespan值。

證明：對于原問題的任意一個可行調度解S，亦即確定了一個無回路單向圖且調度解的makespan值大于或等于的關鍵路徑長度。下面，分兩種情況進行討論：

2）如果該調度解的makespan值Cmax(S)大于的關鍵路徑長度，可以給出一種逆序問題調度解的構造方法：首先，對于逆序問題的工件加工順序方案根據遞推公式(1)計算工件的開工時間并記其最后階段s上完工時間最遲的工件為j'；然后，令根據此種方法得到的可行調度解與原問題的可行調度解之間具有相同的makespan值。

綜上所述，引理得證。

定理1：原問題及其逆序問題是等價的。

證明：1）令原問題及其逆序問題的可行解集合分別為A、B，現在構造一個從集合A到集合B的映射：

由定義2，定理得證。

并且當節點(j,k)在關鍵路徑上的時候，等號成立。

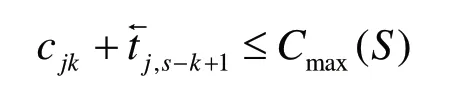
由上述兩點，定理得證。

定理3：對稱定理：逆序問題的逆序是原問題。

3 逆序調度方法

由于常規混合流水車間調度問題及其逆序問題的等價性，可以通過原問題的任意調度算法來求解逆序問題，然后經過解的轉化來獲得原問題的調度解。下面給出此種逆序調度方法的求解框架：

Step1：逆序變換。對于給定的常規HFS調度問題，根據式(3)、式(4)可以確定逆序問題的相關參數（各階段的平行機數和加工時間）。

Step2：利用原調度算法求解逆序問題。

Step3：將求得的逆序調度解“映射”回原來的解空間，得到原問題的調度解。即根據引理1，由逆序調度解的加工順序方案可以得到原問題的一個加工順序方案π，然后根據公式(1)來確定工件的開工時間tjk，進而獲得原問題的完整調度解。

下面，以啟發式算法求解一個10個工件5個階段的算例j10c5a5[2]為例來進行說明。文獻[4]通過仿真實驗說明了采用第2種設備指派規則的NEH算法取得了最好的效果，不妨記此種算法為NF，相應的逆序調度算法記為NB。對于該算例，NF算法在步驟1求得工件加工優先級順序jobOrder=[5 9 3 8 10 1 2 6 7 4]，進一步通過設備指派生成完整的調度解并得到Cmax=126；而通過NB算法求得等價逆序問題的jobOrder= [4 9 3 8 10 7 6 2 1 5]，Cmax=122，并將求得的逆序調度解“映射”回原來的解空間可以得到原問題的解，恰好該調度解為最優解。

4 仿真實驗

以Carlier和Néron提出的77個Benchmark算例[2]作為測試數據，并根據求解難度將其分成兩組：53個易解算例、24個難解算例[3]。本文的算法采用MATLAB語言編寫，運行環境為Win8.1、i3-4130(3.40G)/4G的臺式機。為了評價算法的有效性，采用以下3種指標：百分比偏差PD，運行時間CPU，最優比率（求得最優解的算例個數占該算例集算例總數的比率）。

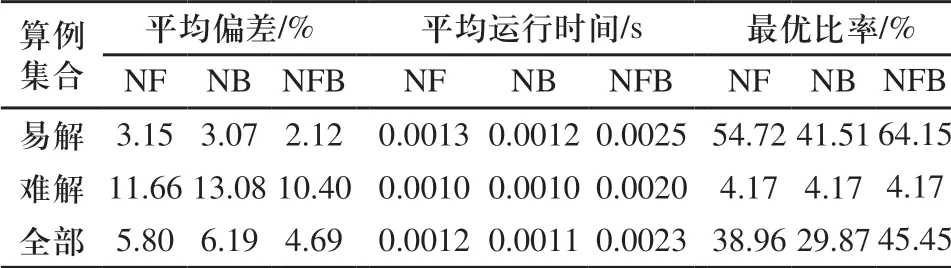
表1 三種算法的計算結果比較

對于這兩組算例，分別采用NF、NB以及正逆序相結合的求解算法（記為NFB）獨立運行1次，對計算結果進行總結如表1所示。由表1可以看出，NF與NB的平均運行時間非常接近；從平均偏差、最優比率來看，NF優于NB。實際上，由于算例集的規模有限且不具有對稱性，不能以此來判斷算法的優劣；根據求解結果可以發現，對于不同的算例NF與NB各具優勢。與NF、NB相比，從平均偏差、最優比率這兩個指標來看，NFB均有較大幅度的提高。雖然NFB需要付出接近2倍的時間代價才可以獲得更好的求解質量，但是其平均運行時間也僅為0.0023s，具有滿足實際需求的計算效率。

5 結束語

本文針對常規混合流水車間調度問題的可逆性展開研究，給出了逆序變換、逆序問題的定義，并從數學角度證明了逆序變換的等價性。在此基礎上，給出了一種逆序調度方法的求解框架，將問題求解方法的數量擴大了一倍，即對于任意已有的調度算法，均可以得到相應的逆序調度算法。特別是對于啟發式方法，通過求解原問題及其逆序問題，只需花費較小的時間代價就可能獲得更好的調度解。然而，在什么條件下去求解等價逆序問題更具優勢，需要進一步去探討。

[1] Gupta J N D.Two-stage hybrid flowshop scheduling problem [J]. Journal of the Operational Research Society,1988, 39(4):359-364.

[2] Carlier J, Néron E.An exact method for solving the multiprocessor flow-shop [J].RAIRO - Operations Research,2000, 34(1):1-25.

[3] Néron E, Baptiste P, Gupta J N D.Solving hybrid flow shop problem using energetic reasoning and global operations[J]. Omega-International Journal of Management Science,2001, 29(6): 501-511.

[4] Guinet A,Solomon M. Scheduling hybrid flowshops to minimize maximum tardiness or maximum completion time[J].International Journal of Production Research,1996,34(6):1643-1654.

[5] 屈國強.瓶頸指向的啟發式算法求解混合流水車間調度問題 [J].信息與控制,2012,41(4):514-521,528.

[6] Nowicki E,Smutnicki C.The flow shop with parallel machines: A tabu search approach[J].European Journal of Operational Research,1998,106(2-3):226-253.

[7] Pan Q K, Wang L, Li J Q, etc.A novel discrete artificial bee colony algorithm for the hybrid flowshop scheduling problem with makespan minimization[J].Omega-International Journal of Management Science,2014,45:42-56.

[8] Chung T P, Liao C J. An immunoglobulin-based artificial immune system for solving the hybrid flow shop problem[J].Applied Soft Computing,2013,13(8):3729-3736.

[9] Li J Q,Pan Q K,Wang F T.A hybrid variable neighborhood search for solving the hybrid flow shop scheduling problem[J].Applied Soft Computing,2014,24:63-77.

[10] Cui Z,Gu X S.An improved discrete artificial bee colony algorithm to minimize the makespan on hybrid flow shop problems[J]. Neurocomputing,2015,148(1):248-259.

[11] Pinedo M.Scheduling theory,algorithms, and system[M].2nd ed. New Jersey:Prentice Hall,2002:133.