基于改進小波神經網絡的短時交通流量預測研究

曹 莉，唐 玲，吳 浩，高 祥，樂英高

(1.四川理工學院a.自動化與電子信息學院;b機械工程學院，四川 自貢 643000;2.東南大學儀器科學與工程學院，南京210096)

引言

城市短時交通流量預測是智能交通系統(Intelligent Transport System，ITS)中的交通規劃和交通流控制中的重要一環，交通流量信息的實時性和可靠性直接影響著交通管理與控制效果，因此短時城市交通流量預測是智能交通領域中的一個重要研究熱點［1-3］。由于智能交通系統是一個復雜的非線性系統，是人、車和路之間組成的一個開放系統，常用的交通系統預測方法通常不能采用確定的線性系統來描述，因此如何有效地預測城市短時交通流量是專家學者致力于解決的難點［4］。目前，交通流量預測的常用方法有簡單移動平均、BP神經網絡、自回歸求和滑動平均(ARIMA)、人工智能算法、群智能優化算法等方法。

近年來，不少學者對短時城市交通流量預測的算法展開了研究，如吳浩勇等［5］將BP神經網絡應用在城市短時交通流量預測中，提出的算法可跟隨交通流量的變化而進行參數調整，提高預測準確度，具有很好的適應性;蔡玥等［6］提出了粒子群PSO優化BP神經網絡算法，將短時交通流量預測精度作為粒子群的適應度函數，通過粒子之間協作獲得預測模型全局最優參數，通過小波神經網絡建立預測模型對短時交通流量模型進行預測;王建等［7］提出一種改進型貝葉斯組合模型，改善傳統貝葉斯組合模型權重計算迭代步長過長的缺陷，提高預測的可靠性，并且具有一定的實用性。

綜述所述，以上這些研究在交通流量預測方面取得了一些進步，但在反映交通流量的復雜性、突變性等方面基本沒有涉及，并且預測精度不高。本文根據近些年新出現的智能計算、群智能算法以及云計算大數據等新技術，引入基于人工蜂群優化小波神經網絡的短時交流流量預測模型，探索尋找短時交通流量一般性規律，并對其進行預測，以其提高預測準確度。

1 人工蜂群算法

在2005年，Karaboga等人從蜜蜂群體覓食過程中群體協作尋找食物的現象得到了啟發，提出了一種新的群智能仿生人工蜂群算法(Artificial Bee Colony Algorithm，ABC)［9］。該算法已經在求解高維函數的最優解、非線性數值運算、組合優化計算等方面取得了不錯進展［10］。圖1給出了詳細蜜蜂采蜜過程。

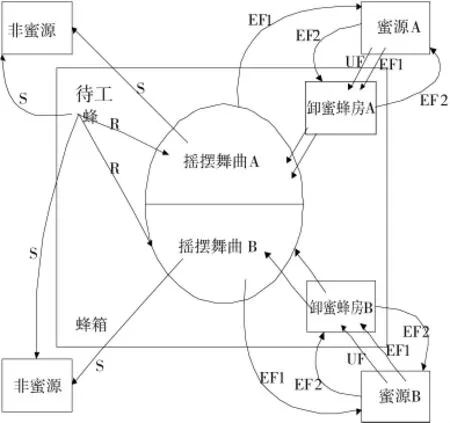
圖1 蜜蜂采蜜工作流程圖

在人工蜂群算法中，主要由偵查蜂(onlookers)，引領蜂(scouts)和雇傭蜂(employed bee)組成。首先由偵查蜂去尋找盡量多的蜜源，引領蜂則對尋找到的蜜源進行標記，標記蜜源的數量和大小，從中選擇比較好的蜜源為初始蜜源，同時釋放與蜜源大小成正相關的路徑信息，以招募其他的跟隨蜂。跟隨蜂則以輪盤賭方式隨機選取適合的蜜源并標記，同時對周邊的蜜源進行對比，選取收益度蜜源進行更新原來的蜜源位置。依次循環，從而找到最優收益度最高的蜜源。人工蜂群算法工作流程圖如圖2所示。

小波神經網絡是以小波基函數為神經元激勵函數的一種前饋型神經網絡［11］。它與常用的BP神經網絡和RBF徑向基神經網絡相比，具有收斂精度更高，結構更加具有可設計性以及收斂速度快等特點。從結構形式來看，小波神經網絡一般分為松散結合型和緊密結合型兩種，本文采用緊密結合型小波神經網絡應用在短時交通流量預測，它的結構為一個三層前饋神經網絡。小波神經網絡模型結構如圖3所示［12］。一般地，小波神經網絡主要包括初始化網絡參數(網絡閾值、連接權值、小波基函數的平移和尺度系數)［13］。訓練樣本集對整個網絡進行訓練，計算輸出誤差的梯度向量，進行誤差方向傳播和修改網絡參數等步驟。

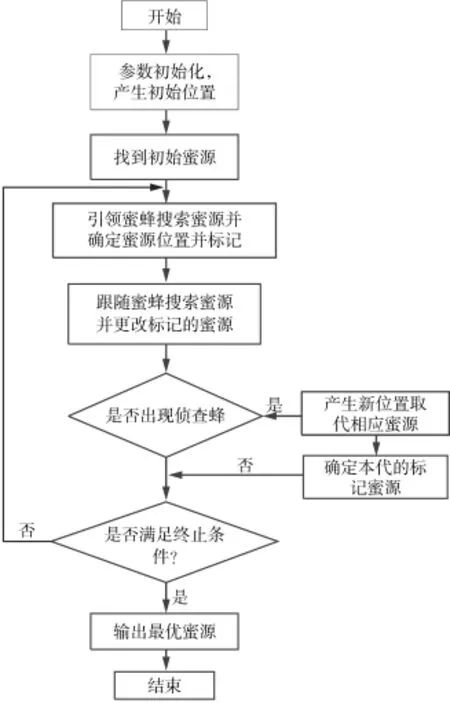
圖2 人工蜂群算法流程圖

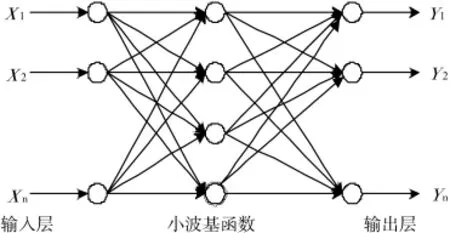
圖3 小波神經網絡模型結構圖

小波神經網絡是根據誤差函數并且采用梯度下降算法來優化調整網絡的連接權值和伸縮平移尺度［14］，但是，單一采用小波神經網絡進行參數優化時，往往很容易使最優解陷入局部極小以及引起振蕩效應，因此將其與群智能仿生算法人工蜂群算法相結合，擴大尋找最優解的范圍，將這兩種算法的優點相互利用，從而獲得更高的短時流量交通預測準確度。

2 基于ABC-WNN流量預測模型

本文首先利用群智能仿生人工蜂群算法的優點——結構簡單、全局尋優性能好的特點，對小波神經網絡權值和閾值進行優化，縮短神經網絡訓練時間，提高算法的泛化能力，這樣便提高了對交通流量的預測精度。在本文提出ABC-WNN算法中，人工蜂群主要優化WNN層數結構、拓撲結構、網絡的最優閾值和權值。WNN層數和拓撲結構主要通過擬合函數的輸入輸出系數來確定，意味著也確定了ABC算法的初始蜜蜂種群選取個體長度和編碼。在ABC算法中，每一個蜜蜂種群里面含有一個待優化的網絡閾值和權值，蜜蜂個體主要以適應函數來計算蜜蜂種群個體的適應度。WNN預測功能則主要是采用ABC算法得到最優蜜蜂種群個體，并對WNN的層數結構、拓撲結構、初始權值和閾值賦值，網絡通過對大量的樣本數據訓練之后預測函數輸出，得到了我們想要的預測模型，以便對城市短時交通流量進行預測，提高算法的預測準確度。

預測算法步驟如下:

(1)初始化，并建立一個小波神經網絡模型。

(2)人工蜂群算法優化小波神經網絡權值和閾值的主要步驟:

①初始化。假設群體規模為SN，生成N個食物源Xi={Xi1，Xi2，…，XiD}，(i=1，2，…，N)的初始種群，D為待優化問題的向量維度。隨機初始化種群:

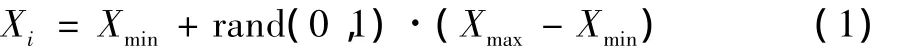
②種群更新。引領蜂在每個蜜源的鄰域生成一個新蜜源，并通過比較二者優劣保留較好的蜜源;跟隨階段，跟隨蜂通過比較蜜源的收益率，以一定的概率選擇蜜源，選中蜜源后，跟隨蜂也在其鄰域生成一個新蜜源，同樣比較二者優劣保留較好解。在這兩個階段，蜜源位置的更新公式為:

其中，k ∈ {1，2，3，…，SN}，j∈ {1，2，3，…，D}，rand(-1，1)為隨機產生(-1，1)之間的數值，它控制 Xij鄰域的生成范圍，隨著搜索接近最優解，鄰域的范圍會逐漸減小。

③蜜源選擇。跟隨階段，跟隨蜂根據蜜源的收益率進行選擇，在這里收益率用適應度值來計算，收益高的蜜源被選中的概率大。概率選擇公式為:

其中，fit(Xn)表示第n個蜜源的適應值，n∈{1，2，3，…，SN}。適應度值計算公式為

其中，f(Xn)為蜜源Xn的目標函數值，根據式(2)在其鄰域內同樣進行新蜜源的搜索，采用貪婪選擇策略擇優保留較優蜜源。跟隨蜂在采蜜蜂的蜜源附近進行搜索，可提高算法的局部開采能力。

④種群淘汰。假設某個解經過連續limit次循環更新之后沒有得到明顯改善，那么就認為這個解陷入局部最優，并放棄此解，相應的引領蜂也變為偵察蜂，并隨機產生一個新的解代替淘汰的解，由

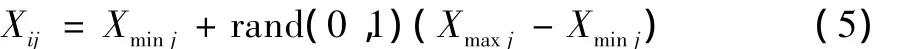
計算產生的新解將其更替，輸出最優解。

(3)如果仿真達到人工蜂群算法初始設置的迭代次數，則蜂群算法優化結束。

(4)將人工蜂群優化后得到的小波神經網絡結構，以及神經網絡的隱含層權值和閾值，運用這個數學模型對城市短時交通流量進行預測，提高短時交通流量預測準確度。

ABC-WNN算法流程圖如圖4所示。

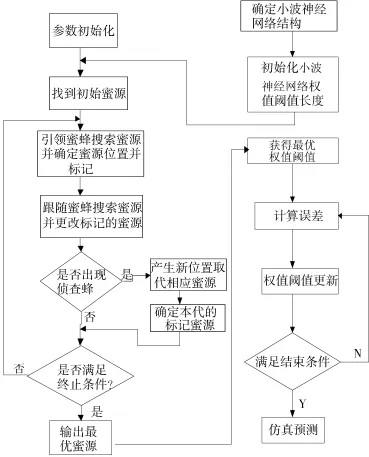
圖4 ABC－WNN算法流程圖

3 仿真結果與分析

根據以上原理，從網上湖北省武漢市ITS數據庫中抽選某條路下午四點半到晚上七點之間的交通流量，每5分鐘的交通流量當作一組數據，調查時間為2013年4月1日到4月15號，總共得到數據450組，其中把1號到12號的390組數據用我們的ABC-WNN算法模型訓練，把訓練好的預測模型對14和15號的60組數據進行預測。為了加快小波神經網絡的訓練速度，避免因數據相差太大對小波神經網絡的預測精度造成影響，對數據進行標準化歸一化處理，將其歸一化到［0，1］區間。具體操作如下:

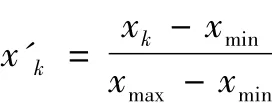
其中，xk表示k時刻的交通流量，x'k表示k時刻經過歸一化后的交通流量數，xmin、xmax分別表示為在k時刻交通流量的最小值與最大值。

短時交通流量預測仿真模型基于Matlab實現，運行在酷睿i3處理器、內存4 G的計算機硬件環境。人工蜂群算法關鍵參數設置為:引領蜂數量為50，跟隨蜂為50，蜂群算法迭代次數為50。給定WNN算法的權值、閾值誤差≤3%時，則人工蜂群尋找到最優解，進化結束，當達到最大的訓練次數時也進化結束。首先用ABC算法優化WNN的最優權值和閾值，之后再用小波神經網絡進行城市短時交通流量預測。神經網絡經典算法小波神經網絡［14］、與本文的ABC-小波算法預測值對比見表1。取其中的15個數據采樣點進行對比，其中小波神經網絡用WNN表示，本文提出的算法用ABC-WNN表示。

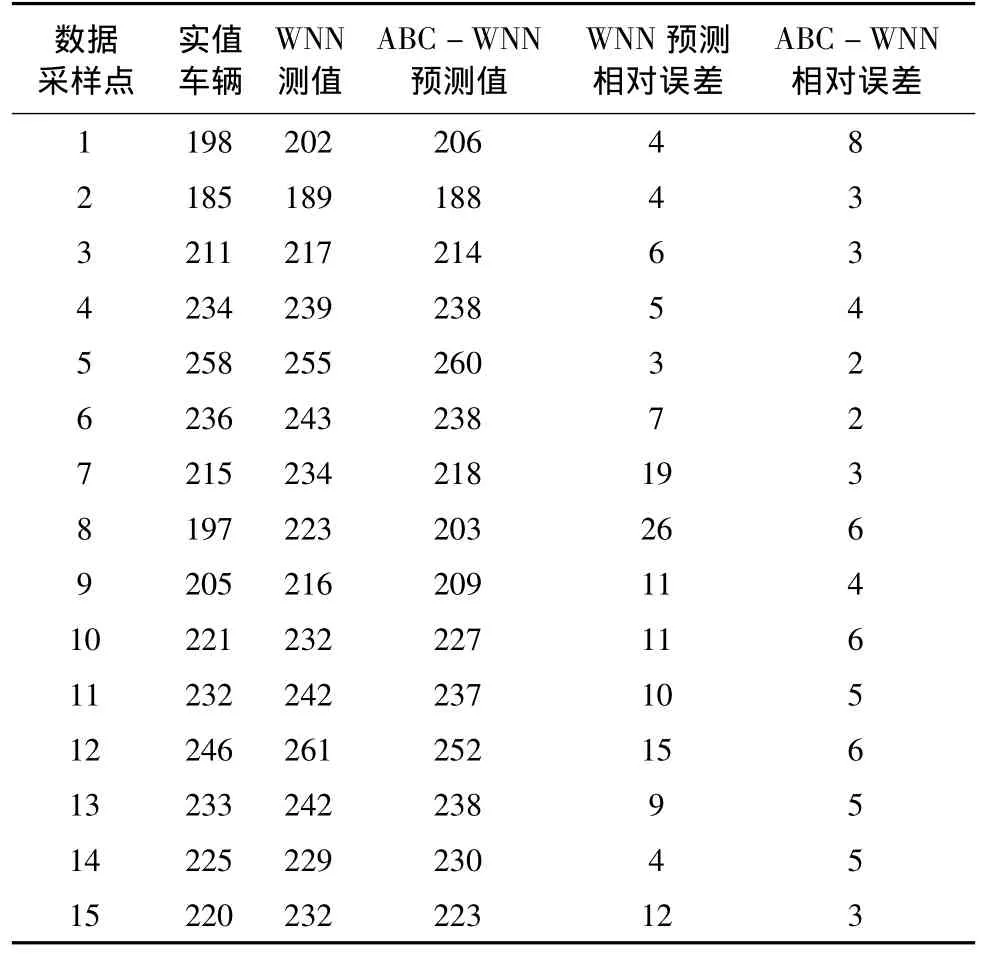
表1 兩種算法預測結果對比

基于ABC算法迭代尋找最優解的迭代過程如圖5所示。可以看出，該算法能以較快的速度尋找到最優解，優化過程是收斂的。

為了體現本文算法性能的優越性，與其他作者提出的算法進行對比分析。選擇普通的WNN算法、文獻［15］里面提到的徑向基神經網絡(RBF)城市短時交通流量預測模型、文獻［16］里提到的粒子群優化BP神經網絡(PSO-BP)預測算法進行對比，得出圖6～圖7仿真結果。圖6是WNN算法，RBF算法、PSO-BP算法和本文的ABC-WNN四種算法的城市短時交通流量預測結果。圖7是四種算法的預測誤差對比。

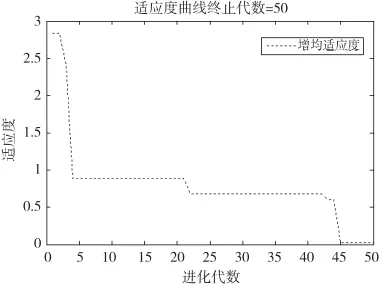
圖5 基于ABC－WNN算法進化代數

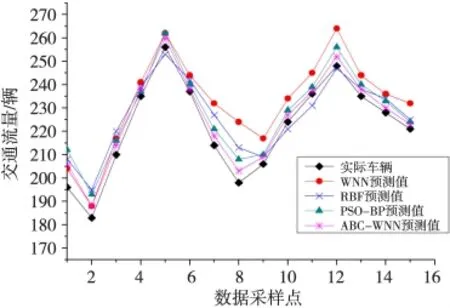
圖6 PSO－BP、WNN、RBF與ABC－WNN預測對比

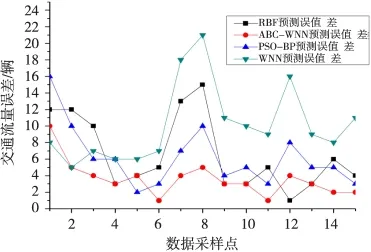
圖7 PSO－BP、WNN、RBF與ABC－WNN誤差對比

從圖6～圖7可以看出，四種算法的誤差從大到小的順序是WNN算法、RBF神經網絡算法、PSO-BP算法和本文提出的算法。本文提出的算法誤差最小，最接近實際城市交通流量;同時還看出，不同的采樣點，算法的交通流量預測誤差也不一樣。

為了更加直觀地體現算法之間的差異，對四種算法產生的交通流量預測誤差數據進行量化，用均方根誤差(RMSE)和仿真耗時對其說明。其中

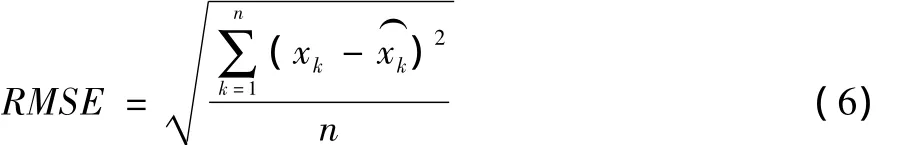
其中，xk為k時刻的觀測城市交通流量，為t時刻的預測城市交通流量，n為整個預測時間段中的預測城市交通的總數據量。四種算法RMSE值以及仿真耗時見表2。

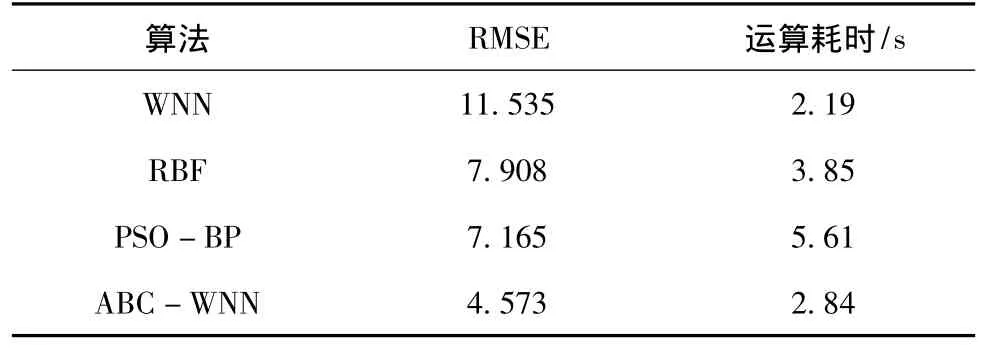
表2 幾種預測模型RMSE值和時間對比

從表2中可知，本文提出的ABC-WNN的RMSE值最小，PSO-BP算法次之、RBF算法第三，WNN誤差值最大，其中PSO-BP算法與RBF算法的誤差值相近。同時PSO-BP算法的模型運行耗時最長，主要因為粒子群尋優過程中計算量龐大、計算復雜，運行耗時最長。從以上仿真結果來看，本文提出的基于ABC-WNN算法的預測模型，計算出來的預測值更接近的真實城市交通流量，因此本文提出的算法是一種有效可靠的短時城市交通流量模型預測方法。

4 結束語

短時城市交通流量預測問題是城市可持續發展的重要問題，是智能交通發展的關鍵技術，能很好地緩解道路擁擠情況，保證路面的通暢與提高路面利用率。本文提出基于人工蜂群優化小波神經網絡的權值和閾值，建立最優的預測模型，提高算法的預測準確度。通過算法仿真對比，提出的算法具有較高的預測精度，但由于優化的神經網絡里面的訓練模型樣本數量較少，同時城市交通流量預測容易受到外界環境，突發事件影響，預測效果還存在不確定因素和不足的地方，下一步結合新的群智能算法對短時城市交通流量預測問題展開更加深入的研究。

[1] 曹政才,韓丁富,王永吉,等.面向城市交通網絡的一種新型動態路徑尋優方法[J].電子學報,2012,40(10):2062-2067.

[2] 王文奇,劉保縣,李麗,等.中國西部山區交通設施震害分析(英文)[J].四川理工學院學報:自然科學版,2015,28(1):41-45.

[3] 謝軍,吳偉,楊曉光,等.用于短時交通流預測的多項式分布滯后模型[J].同濟大學學報:自然科學版,2011,39(9):1297-1302.

[4] 溫勝強,周鵬飛,康海貴,等.基于灰色理論與 BP神經網絡的交通運輸量組合預測研究[J].大連理工大學學報,2010,50(4):547-550.

[5] 吳浩勇,叢玉良,王宏志.基于神經網絡的交通參數預測方法[J].吉林大學學報:信息科學版,2005,23(11):570-572.

[6] 蔡玥.短時交通流量預測的IPSO-BPNN算法[J].計算機工程與應用,2012,48(27):240-242.

[7] 王建,鄧衛,趙金寶,等.基于改進型貝葉斯組合模型的短時交通流量預測[J].東南大學學報:自然科學版,2012,42(1):162-167.

[8] 陳小紅,錢大琳.城市道路交叉路口的擁堵預測[J].華南理工大學學報:自然科學版,2010,38(7):72-77.

[9] Abu-Mouti F S,El-Hawary M E.Optimal distributed generation allocation and sizing in Distribution Systems via Artificial Bee Colony Algorithm[J].IEEE Transactions on Power Delivery,2011,26(4):2090-2101.

[10] Wang Yajun,Chen Wen,Tellambura C.A PAPR reduction method based on Artificial Bee Colony Algorithm for OFDM signals[J].IEEE Transactions on Wireless Communications,2010,9(10):2994-2999.

[11] 黃永紅,徐勇.基于小波神經網絡的某邊坡預測研究[J].四川理工學院學報:自然科學版,2011,24(3):370-372.

[12] 姚毅,陳光建,賈金玲.基于模糊神經網絡算法的機器人路徑規劃研究[J].四川理工學院學報:自然科學版,2014,27(6):30-33.

[13] 杜道淵,柏宏斌,周鋒.基于BP神經網絡自貢房地產價格走勢預測[J].四川理工學院學報:自然科學版,2011,24(3):366-369.

[14] 徐鑫鑫,蘇華友,張春萍.BP神經網絡在基坑周邊地表短期沉降預測中的應用[J].四川理工學院學報:自然科學版,2013,26(2):53-56.

[15] 張海燕,唐建芳.基于RBF神經網絡的語音情感識別[J].四川理工學院學報:自然科學版,2011,24(5):552-555.

[16] 李松,劉力軍,翟曼,等.改進粒子群算法優化BP神經網絡的短時交通流預測[J].系統工程理論與實踐,2012,32(9):2045-2049.