防水工程質量保證保險費率厘定研究
楊 帆 洪文霞 魏小朝 楊 昭
青島理工大學管理學院
?
防水工程質量保證保險費率厘定研究
楊 帆 洪文霞 魏小朝 楊 昭
青島理工大學管理學院
建筑行業素有“結構第一,防水第二”的說法。建筑防水質量的優劣直接影響建筑結構的安全性,更關系到業主的日常使用和生命財產安全。但我國防水行業亂象叢生,質量問題亟待解決。而建立防水工程質量保證保險體系是徹底解決我國目前防水質量問題的必由之路。
一、引言
防水工程作為建筑工程的一個重要環節,不僅關系到建筑物的結構安全性能,對建筑的使用功能及環境衛生等也有很大影響。保證建筑物或構筑物在合理的設計使用年限內,能夠正常使用,避免遭受水的侵蝕,為使用者提供一個舒適安全的環境,是建筑防水工程最重要的功能(柳明,2014)。近年來,我國城市建設步伐的加快推動了建筑行業的迅速發展,各類工程項目層出不窮,而一些建筑公司為了謀取利潤,對質量的管理流于表面,往往只做表面文章,建筑滲透問題頻現,不僅影響人們的日常使用,也使用戶與業主之間矛盾不斷。為了解決防水工程的質量問題,國外探索出了一條建立防水工程質量保證保險制度的道路,防水工程的質量得到了改善。而目前我國針對建筑防水工程質量的問題采取的是5年保修期制度和5%的質量保證金制度。但是5%的質量保證金與建造劣質工程所帶來的利潤相比,微不足道。5年保修期相對于住宅的70年產權也明顯偏短。事故代價過低使一些建筑企業鉆了制度的空子,出現滲漏只要修補就行,保修期和質保金變成了防水工程質量問題的許可證。學習國外的先進經驗,建立防水工程質量保證保險制度才是解決建筑防水工程質量問題的終極之道(朱東清,2014)。
如果能探尋一個合理厘定防水工程質量保證保險費率的方法,作為工程質量保證保險的附加保險進行推廣,將會對建筑企業起到一定的約束作用,同時促進防水材料供應商的優勝劣汰,從根本上改善我國防水工程的質量狀況。鑒于此,本文引入統計理論確立了基準費率,并以模糊綜合評價法(FCE )對基準費率進行修正。
二、計算防水工程質量保證保險基準費率
(一)基于統計理論的基準費率厘定
統計理論是傳統費率厘定的精算定價方法。其基本原理為:
p=E(S)=E(N)·E(X)
(1)
i0=純保費率=P/n
(2)
其中,P代表純保費;S為賠付成本的隨機變量;i0代表基準費率;N代表理賠頻率;X代表一次索賠的賠付額;n代表風險單位個數。
(二)估算賠付額
對損失數據進行統計分析,運用SPPS軟件擬合出損失數據的分布函數F(X)及損失密度函數f(x),建立概率密度曲線。由此得到保險標的的單位期望賠付額E(X)。
(三)估計理賠頻率
《2013年全國建筑滲漏狀況調查項目報告》顯示,國內主要城市建筑屋面滲漏率高達95.33%。有必要將建筑防水工程質量保證保險在建筑行業新建項目強制推行,即該行業所有建筑企業均作為投保人,則風險單位個數可近似假設為該行業建筑企業數。運用crystalball軟件進行擬合得到期望理賠頻率E(N)。
最終由公式(2)計算基準費率i0。
三、計算防水工程質量保證保險風險調整系數
i0是基準費率,是基于共性的費率,必須重新調整費率結構,即由一個調整系數乘以基準費率得到基于個體的保險實際費率:
i=i0×a
(3)
(一)建立防水工程質量風險評估指標體系
本文從建設單位、材料供應商、項目特性三個方面綜合考慮對防水工程質量風險的影響,建立了因素集X=(X1,X2,X3),因素集下的指標集:Xi=(xii,xi2,…,xij),其中,i=1,2,3,j為因素下指標的個數。構建的防水工程質量風險評估指標層次結構體系如下表所示。
(二)定義評價集
定義評價集是為了確定防水工程質量保證保險費率調整系數,我們將建筑工程滲透風險分為五個等級:V=[V1,V2,V3,V4,V5]=(很低,較低,一般,較高,很高)。風險高于平均水平則調整系數大于1,風險越高系數越大;反之,風險低于平均水平時,調整系數小于1,風險越低系數越小。則對應的風險評價值C=(0.6,0.8,1.0,1.2,1.4)。
(三)防水工程質量風險模糊綜合評價
模糊層次分析法以模糊數學隸屬度理論為基礎,將定性評價轉化成定量的方式處理,能很好地解決難以量化的問題,但在指標權重分配上主觀性較強。而熵權法利用各指標的變異程度,通過計算各指標的信息熵來進行權重分配,充分反映了指標數據自身所攜帶的信息,更具客觀性。因此,本文提出熵權與模糊層次分析法耦合的風險評估模型,計算過程如下:

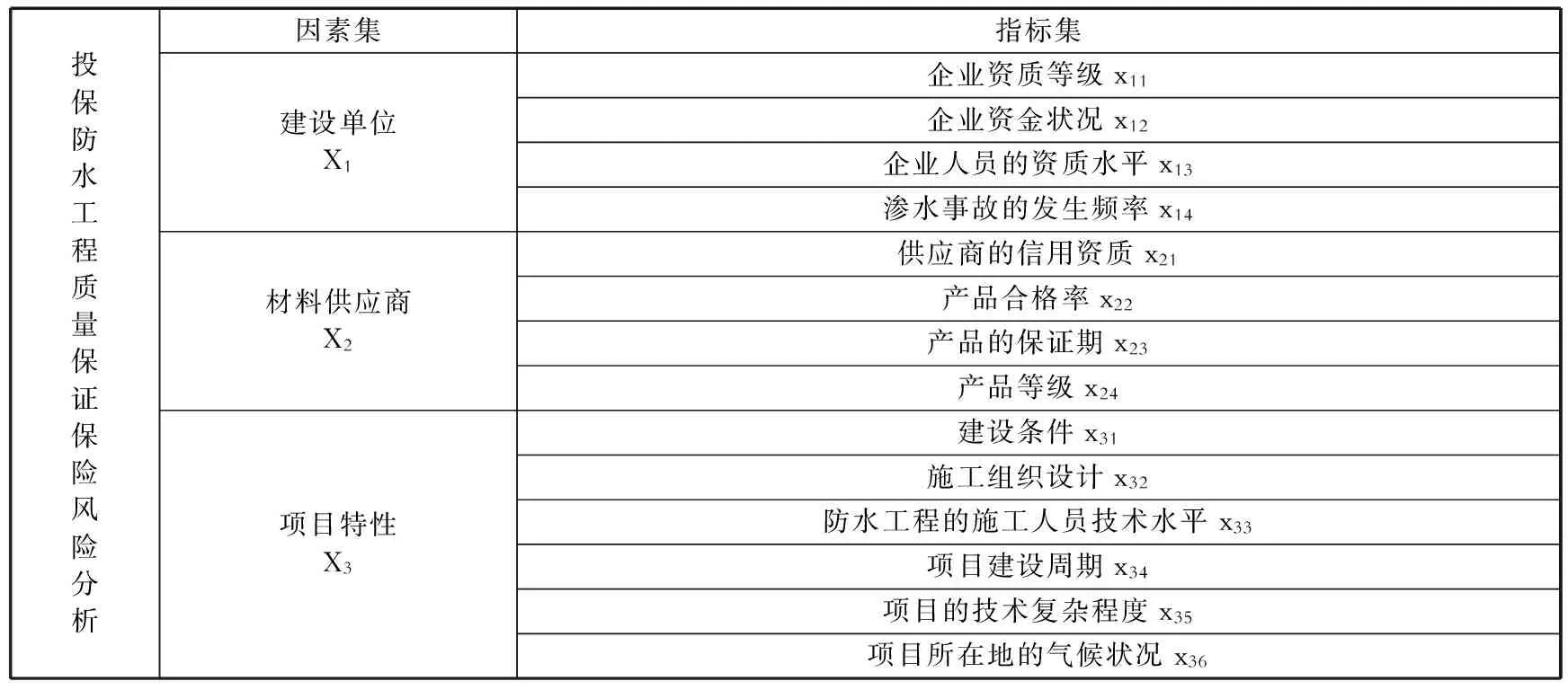
表 防水工程質量保證保險風險評估指標體系
防水工程利益相關方眾多,不同領域的專家對防水工程質量風險會有不同的認識,綜合各方意見有利于確保風險評估的客觀公正性。故選取分別來自政府、防水協會、工程建設專家等20人組建專家組對某建筑防水工程的質量風險進行評價。得到該項目防水工程風險的初始化指標集隸屬矩陣:
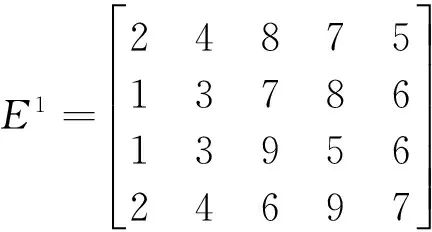
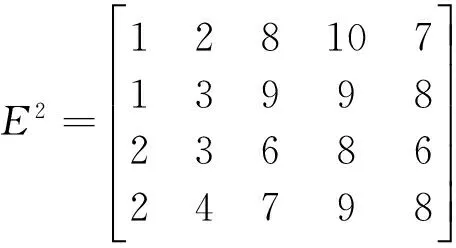
因子集X中各因子在防水工程質量風險綜合評價中的重要性程度不同,不同權重會對評價結果有不同程度的影響,須對參與評價的指標因子進行賦權。
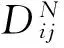
(4)

(5)
4.由熵權法計算各指標的權重,公式如下:
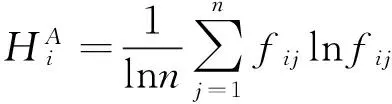
(6)
(7)
5.由公式(8)計算加權規范化指標集隸屬矩陣:
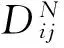
(8)
因素X1下的指標加權規范化隸屬矩陣計算過程如下:
由公式(4)計算E1歸一化隸屬矩陣D1:
由公式(5)計算E1規范化隸屬矩陣R1:
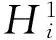
由公式(8)計算指標評價向量:
同理可得:
6.確定因素集隸屬矩陣B:

7.由公式(5)、(6)、(7)計算因素集的權重向量:

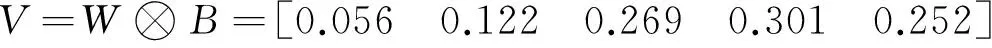
8.計算風險指數即調整系數:
a=V×CT=1.114
(四)評價結果
保險產品作為特殊的商品,合理厘定具有差別化的防水工程質量保證保險費率是形成該保險市場的前提。通過對該項目的防水工程質量風險的評估得出其風險高于平均水平,則其保險費率i=i0(基準費率)×1.114。
四、結論
防水工程質量保證保險作為我國一個新興的保險類型,在制度和政策上都有很多的不足,本文針對防水工程質量保證保險費率的合理厘定,以統計理論為基礎,采用修正系數的形式建立了防水工程質量保證保險費率的厘定模型。本文主要結論有:
第一,引入統計理論,針對新型險種費率的厘定具有科學性和適應性,同時滿足保險費率厘定原則的大數法則。
第二,通過運用模糊綜合評價法,從保險公司的角度進行費率的修正。這樣做同樣也具有科學性,同時體現了防災防損的特性,為構建健康穩定的建筑行業環境提供了保障。
第三,通過研究分析,得出建筑防水工程質量保證保險費率的厘定程序和基本計算模型,有利于我國建筑防水工程質量保證保險的推廣。
第四,對于基準費率的厘定,文章僅是給出了計算模型,而未進行實際驗算,且基準費率為純保費率,未考慮利潤、管理等其他因素。故精確的基準費率厘定有待進一步研究。

