基于支持向量機的車輛軸承故障檢測方法研究

馬家威 王業矗 劉 雋 王升安 姜英姿

（徐州工程學院 江蘇徐州）

在車輛系統中旋轉機械是其最常見的機械設備也是其關鍵性設備，對整個車輛系統的安全起著至關重要的作用。如果旋轉機械出現故障，可能會導致整個車輛系統癱瘓，造成巨大的經濟損失與人員傷亡。因此，選取最常見的軸承零件作為研究對象，利用模式識別技術對其進行故障診斷。

一、車輛系統故障分析

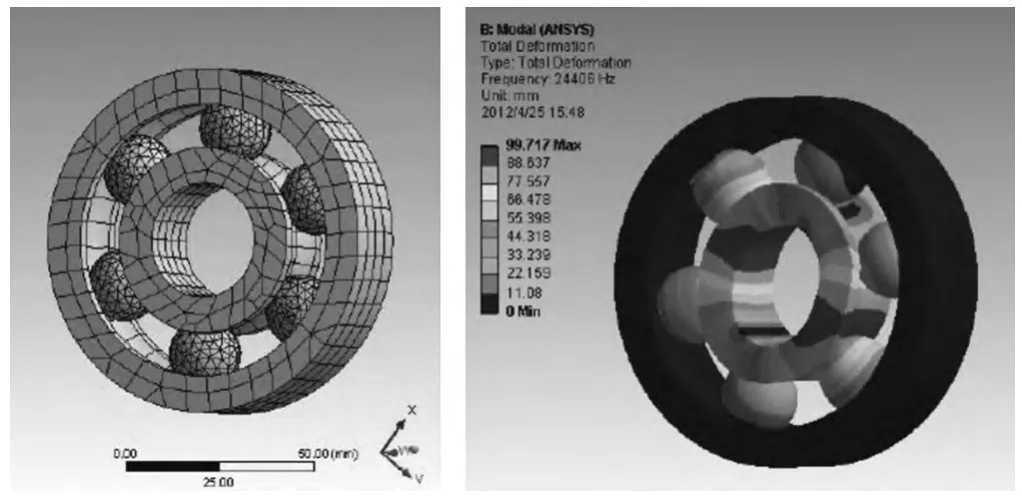
圖1 滾動軸承的有限元分析

對于車輛機械系統而言，根據故障產生的部位不同可以分為3個部分：機械零部件故障；控制系統故障和潤滑油品質下降引起的故障。在這3種故障中，相對易發生且難檢測的當屬于機械零部件故障。機械零部件的使用壽命一般具有離散性，同樣的機械零件，即使材料、工藝、生產設備等都相同，使用壽命也存在著較大的差異，在實際的使用過程中，有些機械零件沒有達到使用壽命就已經報廢，而有些機械零件即使使用時間超過其規定使用壽命卻依然運行良好。

在車輛機械零件中，軸承是主要的承力單位，工作環境較差且承受大負載，屬于易損耗零件，由于實際生產或工作環境中，軸承的生產精度不高，裝配不當或者沖擊載荷過大等影響，軸承主要失效形式有疲勞損壞、磨損、腐蝕、破損好壓痕，任意一種失效形式的產生都將對軸承的壽命造成致命的影響。

以型號為6406的滾動軸承為例，利用Pro/E繪制三維模型，然后對其做有限元分析，模型的內圈、外圈及滾動體的材料選用軸承鋼GCr15，密度為7830 kg/m3，彈性模量為E=2.06×105MPa，泊松比μ=0.3。軸承的外圈固定不動，內圈隨軸旋轉，內圈由軸過盈配合不發生相對運用。當振動頻率達到15380 Hz時，其主振形如圖1所示。

從圖中可以看出，當振動頻率達到15 380 Hz時，軸承內圈發生嚴重損壞變形，由此可以看出低階模態振型對滾動軸承的振動影響較大，尤其在低階固有頻率下的時候，形狀變化十分明顯。

當軸承發生微小損壞的時候，如軸承的表面出現點蝕、劃痕、凹陷，此時軸承每振動一次都會產生一次振動，并且這種振動具有周期性，軸承的轉速越大，振動周期越小，軸承損壞的尺寸越大，振動的幅度也越大。所以，軸承出現損壞時，軸承的故障特征頻率為其工作產生的頻率。令f0表示軸的轉動頻率，單位為r/min，則根據軸承的幾何尺寸和軸承的轉動頻率，可以計算出故障特征頻率。

滾動體通過軸承外圈損壞點的頻率fi：

滾動體通過軸承內圈上一損壞點的頻率fj：

滾動體上一損壞點通過內圈或者外圈的頻率fb：

保持架故障頻率fc：

式中 N——滾動體個數

d——滾動體直徑，mm

D——軸承的節徑，mm

φ——軸承壓力角，rad

當軸承發生局部損壞時，軸承的其他元件會在工作時周期性地撞擊損壞處，沖撞會引起軸承其他部分被激勵，從而產生一系列沖擊振動。實際工作環境中，軸承滾動體不是完全純滾動而且滾動體安裝后也會存在誤差，因此，譜峰的頻率并不一定等于其理論值。所以在根據滾動軸承的頻譜圖判斷其故障時，需要在理論值的附近尋找相對較接近的頻率，然后根據尋找的頻率對其做出判斷。

二、支持向量機（SVM）理論基礎

對于滾動軸承的故障監測可以看成是判斷軸承的狀態，把軸承的狀態分為正常與故障兩種，那么滾動軸承故障監測就變成了依據其振動參數的一種模式識別，其識別結果只有兩種--正常和故障，而支持向量機在模式識別方面所需樣本相對較少且分類精度高。因此，采用支持向量機，對軸承狀態進行識別并判斷其故障特性。

支持向量機是20世紀90年代初Vapnik等人，根據統計學習理論和結構風險最小化為依據提出的一種新的機器學習方法，該方法善于解決樣本數量少、非線性及高維分類等復雜樣本分類情況。其優化目標是置信范圍最小，約束條件是訓練誤差最小，具有凸二次優化的特點，因此找到的極值解一定是全局的最優解。其主要思想是把輸入的參數樣本經過非線性變換從而轉換到另外一個特征空間，然后在這個新的空間中尋找樣本的最優分類面。

假設有共有K個樣本xi和兩個類別yi，i=1，2……K，yi∈{1，-1}，其分類間隔為2/||ω||。那么要使分類間隔最大，則等同于要求/||ω||2最小，所以使分類間隔最大的優化問題可以轉化為二次規劃問題，其目標函數為：

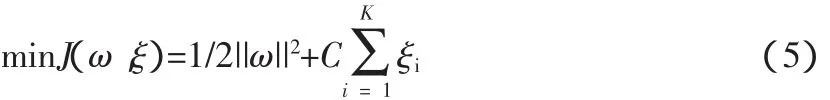
約束條件為：

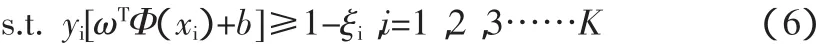
（5）式中，C為指定常數，可以起到控制對錯分樣本懲罰度的作用，使得錯分樣本的比例與算法復雜度之間保持平衡。其中ξi為松弛因子，Φ為非線性變換函數，由于分類樣本可能存在線性不可分的情況，因此，為了保證分類的正確性，應該滿足ξi≥0（i=1，2，3……K）。

三、基于SVM的滾動軸承故障檢測

基于SVM的滾動軸承故障檢測主要思想是對采集的振動信號進行分解，提取最具代表性的特征向量，然后輸入到SVM模式識別模型中，進行故障類型識別。

樣本參數為振動信號 ，利用正則化公式對其進行預處理：

式中 μ——樣本的均值

σ——樣本的標準差。

檢測數據可以看成是二元樣本：

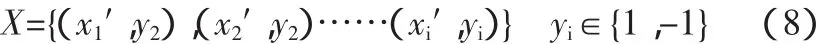
假設當x1′=ω1的時候yi=1，表示軸承的故障狀態，當x1′=ω2的時候yi=-1表示軸承的正常狀態。建立以下分類為兩類的模式判別函數：

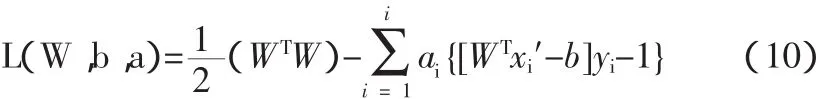
令ai為Lagrange乘子，b0是分類閾值，且：

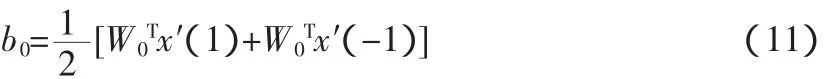
則分類規則函數為：

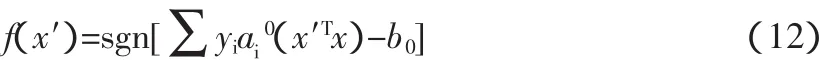
四、算例

選用美國凱斯西儲大學電氣工程實驗室所采集的數據驗證以上方法的可行性。軸承的型號SKF6205，采樣頻率12000 Hz，軸承轉速1500 r/min。對滾動軸承的內圈故障采集數據，以驗證判別模型的合理性。

利用MATLAB編寫支持向量機程序并將數據帶入，得到支持向量機的訓練結果與測試結果。在支持向量機的訓練結果中，內圈故障10個樣本正確識別出9個，訓練結果準確分類率為90%，在分類結果中，內圈故障10個樣本正確識別8個，正確識別準確率為80%，結果表明支持向量機對軸承的故障檢測具有良好的效果。

五、結論

針對車輛機械故障產生的主要原因，著重研究滾動軸承在車輛工作過程中的損壞情況，利用ProE分析得低階模態振型對滾動軸承的振動影響較大，尤其在低階固有頻率下，形狀變化十分明顯。將軸承的狀態分為兩類，分別是正常與故障，利用支持向量機對其進行模式識別，以振動信號作為樣本數據，計算結果表明，支持向量機在軸承故障檢測中具有良好的分類效果與準確性。