基于小波基稀疏信號特征提取的軸承故障診斷

樊 薇， 李 雙， 蔡改改， 沈長青， 黃偉國， 朱忠奎

(1.蘇州大學城市軌道交通學院， 江蘇 蘇州 215131； 2.蘇州大學機電工程學院， 江蘇 蘇州 215021)

基于小波基稀疏信號特征提取的軸承故障診斷

樊 薇1， 李 雙1， 蔡改改1， 沈長青2， 黃偉國1， 朱忠奎1

(1.蘇州大學城市軌道交通學院， 江蘇 蘇州 215131； 2.蘇州大學機電工程學院， 江蘇 蘇州 215021)

軸承弱故障振動信號中的瞬態成分極易被強背景噪聲湮沒而無法及時檢測，結合稀疏表示原理提出一種基于小波基的稀疏信號特征提取方法，從而實現信號中瞬態特征成分的提取。通過構建原始信號瞬態成分稀疏表示模型，對原始信號采用相關濾波法獲取最優小波原子，并構建最優冗余小波基底，實現小波基與信號故障特征的最優匹配；設計二次嚴格凸函數并運用優化最小(Majorization Minimization,MM)算法求解模型中的目標函數，將信號中的瞬態沖擊成分轉化為稀疏表示系數，實現強背景噪聲下弱特征的有效提取。仿真信號及軸承微弱故障試驗驗證了該方法能有效地檢測和提取強背景噪聲下的微弱瞬態成分。

故障診斷； 軸承； 稀疏表示； MM算法； 瞬態成分

引 言

滾動軸承運行過程中損傷點與其他元件接觸時產生的周期性沖擊是判斷軸承局部損傷故障的關鍵特征信息之一。運用有效的信號處理方法分析振動信號，獲得反映旋轉機械設備運行狀態的瞬態特征信息，是旋轉機械故障診斷最為廣泛的方法之一[1-2]。然而，在信號采集過程中，由于電機、信號采集系統等設備的干擾以及隨機噪聲等不可避免因素的影響，實際的振動信號，尤其是微弱故障振動信號往往會被不同程度的噪聲所污染，給故障特征提取帶來了困難。因此，如何從含強背景噪聲的信號中提取出真實的機械振動信號，是故障診斷研究工作的主要任務，也是旋轉機械設備故障診斷的關鍵難題之一。

近年來，基于稀疏表示的特征提取方法在圖像處理等領域得到了廣泛的應用[3]。Mallet和Zhang首先提出信號在過完備庫上分解的思想[4]，通過在過完備庫中自適應的選擇與信號最相似的原子，并使選擇的原子個數盡可能的少，從而得到原始信號非常簡潔的表達，即稀疏表示。稀疏表示方法對自然信號用少量的表示系數捕獲反映信號特征的主要成分，表達簡潔、易于數據存儲，已成為圖像處理[5]、信號處理[6]、模式識別[7]等領域強有力的工具之一。Selesnick應用稀疏表示的思想，基于正弦基底和分裂增廣拉格朗日收縮算法(Split Augmented Lagrangian Shrinkage Algorithm, SALSA)，將非整數周期正弦信號的特征頻率成功提取出來[8]；Cai等針對齒輪故障信號的特點，提出基于可調Q因子小波變換和SALSA的信號稀疏分解方法，并成功檢測出齒輪振動信號中的瞬態成分[9]。以上研究表明：信號在冗余基底上的稀疏表示研究主要集中在兩方面：1)如何構造適合信號特點的冗余基底；2)如何設計優化算法求解稀疏表示問題。

一方面，正弦基底和可調Q因子小波并不適應于機械設備中單邊衰減沖擊響應波形的提取，而原子庫的選取對于信號表達的稀疏度影響十分顯著；另一方面SALSA迭代過程中需兩次優化目標函數，運算速度慢，影響稀疏表示方法的運算效率。考慮到由Strang G構造出的Laplace小波與單邊衰減沖擊響應波形最相似[10-11]，而MM算法[12]迭代過程中僅需優化一次目標函數，運算速度較快，本文提出一種新的稀疏信號特征提取方法。首先構建信號瞬態成分稀疏表示模型；再通過相關濾波法選取最優Laplace小波原子，并張成具有不同時移參量的Laplace冗余小波基底，構成稀疏表示基底；然后在選定表示基底的基礎上，采用MM算法優化目標函數，求解稀疏表示模型，獲得瞬態成分在該基底上的稀疏表示系數，將原始信號中的瞬態沖擊響應成分轉換成少量非零系數。運用包絡解調方法對重構信號進行分析，能較準確地提取軸承故障特征頻率。進一步通過不同信噪比下仿真信號與重構信號的相關度驗證該方法在強背景噪聲下提取弱特征的適應性，并通過提取軸承在弱故障狀態下的故障特征頻率驗證該方法的有效性。

1 信號瞬態成分稀疏表示

1.1 瞬態成分稀疏表示模型及問題

稀疏表示的基本思想是選擇冗余基取代傳統方法中的正交基，而基底的選擇應盡可能的包含被表達信號所含有的信息結構，則從冗余基中選擇具有最佳線性組合的若干原子就可以稀疏表示被表達信號，該過程可以表示為逼近過程

(1)

從稀疏角度出發，希望在xr達到最小的情況下得到信號x最稀疏的表示結果。可構造稀疏表示模型如下

(2)

式中α=[α1,α2,…,αK]∈RK×1為稀疏表示向量，D=[d1,d2,…dK]∈RN×K(K>N)為冗余基底，di為D中的原子，零范數(‖·‖0)表示非零元素的個數。采用正則化方法，通過參數λ平衡稀疏性和稀疏表示誤差

(3)

式中l0范數優化問題非凸，是NP-hard問題[8]。Candes和Tao[13]證明只要足夠稀疏，上式l0范數可以轉化為l1范數的非嚴格凸優化問題

(4)

上述模型中的根本問題在于：1)如何構造適合信號瞬態成分特點的冗余基底D，使信號表示系數稀疏度高；2)如何設計優化算法求解稀疏表示問題，使稀疏表示運算速度快。

1.2 基于相關濾波的冗余基底構造

為解決瞬態特征成分稀疏表示方法在冗余基底選擇上的問題，引入相關濾波法，提取出瞬態成分波形特征參數及最優小波原子；再將提取出的小波原子張成具有不同時移參量的最優小波原子庫，即冗余基底，作為稀疏表示基底。

針對實際信號中的單邊衰減特性成分，選取與沖擊響應波形具有類似衰減性質的Laplace小波作為冗余基底D中的原子，冗余基底D為具有不同時移參量的基函數庫。Laplace小波為非正交小波，采用復指數形式對信號進行小波變換會增加數據的復雜度和冗余性，考慮到待檢測信號為實信號，通常使用Laplace小波實數形式，其解析表達式為

d(t,τ)=ψ(f,ζ,τ,t)=ψγ(t)=

(5)

式中f∈R+表示頻率，ζ∈[0,1)?R+表示粘滯阻尼比，系數A用來歸一化小波函數，Ws表示小波支撐區間。

根據信號稀疏表示的特性，由于冗余基底D是由具有不同時移參量的Laplace小波原子構成，冗余基底中每一個原子與信號中的瞬態沖擊響應成分匹配度較高，因此信號中的瞬態成分可以用冗余基底D來稀疏表示，而信號采集過程中的噪聲信號與冗余基底D中的原子匹配程度較低，則不能用冗余基底D中的原子稀疏表示，因此該方法能實現強背景噪聲下弱故障特征的提取。

1.3MM算法

為提高瞬態特征成分稀疏表示方法的運算速度，引入MM算法，將非嚴格凸優化問題轉換成簡單嚴格凸優化問題，通過優化迭代算法求解目標函數，獲得被表達信號在冗余基底D上的稀疏表示系數。

非嚴格凸優化問題式(4)可以表示為

(6)

MM算法[16]通過求解一系列簡單優化問題Gi(α)來逼近原問題的解，即

(7)

(8)

(9)

式中 ‖·‖*表示復共軛轉置，Λi=diag(|αi|)為對角陣。保持數據保真項不變，Gi(α)可以表示為

式中 參數λ的選取準則可參考文獻[17]。

由此得到瞬態成分稀疏表示模型(4)的快速求解算法，具體步驟如下：

2)按不同時移變化張成最優冗余小波基D(t,τ)。

3)輸入原始信號x，參數λ；設定算法停止閾值ε。

4)初始化。令迭代計數變量i=0，初始值α0=D*x。

5)計算對角矩陣Λi。

6)利用代數求導法求解式(10)，得到αi+1。

2 仿真分析

為驗證Laplace小波基底下瞬態成分稀疏表示的有效性，下面對循環多沖擊響應仿真信號進行分析，仿真信號表達式為

式中 時間t∈[0,1]s，f0=200 Hz，ζ0=0.05，τ0=0.1 s，T0=0.2 s，n(t)為高斯白噪聲，An為噪聲幅值。取An=0.55 m/s2，信噪比為-11.77 dB，用2 000 Hz采樣頻率對x(t)離散化。取拉格朗日乘子λ=5.04，設定算法停止閾值ε=2.5×e-6。通過Matlab仿真，分析小波基底下的稀疏表示對信號瞬態沖擊時間的辨識和對噪聲的抑制能力。當信噪比取SNR=-11.77 dB時，仿真信號如圖1所示。

圖1 仿真信號波形Fig.1 The simulated signal

對圖2(c)重構信號進行包絡解調分析得到其包絡譜圖如圖3所示，圖3表明重構信號的特征頻率為5 Hz，與理論值一致。

利用原始信號與重構信號之間的相關系數(Correlation Coefficient,CC)作為重構信號優劣程度的評判標準。相關系數表達式為

(13)

相關系數越接近1，表明重構信號與原始信號的相似程度越大。對圖2(c)和圖1(a)信號進行相關性計算得重構信號與原始信號的相關系數為0.904，說明該方法不僅能確定含噪信號中沖擊響應的發生時刻，且重構信號與原始信號成分非常接近。

為進一步驗證該方法對沖擊響應發生時刻的辨識能力，表1列出了不同噪聲水平下辨識得到的沖擊響應時刻，并給出了對應的重構信號與原始信號的相關系數。表中An，SNR分別表示噪聲的幅值和對應的信噪比，ti為該方法辨識得到的沖擊響應時刻，CC為重構信號與原始信號的相關系數。信噪比定義為SNR=10×lg(Ps/Pn)，其中Ps和Pn分別為信號和噪聲的能量。

表1表明，在信噪比達到-13.87 dB時，辨識得到的沖擊響應時刻與原始信號的沖擊響應時刻誤差較大，重構信號與原始信號的相關度也比較低。但隨著信噪比的提高，該方法重構的信號與原始信號的相關度也相應提高，信號重構的效果也更好，能較準確地辨識出沖擊響應成分的發生時刻，較好的恢復原信號。

圖3 重構信號包絡譜圖Fig.3 The envelope spectrum for the reconstructed signal

3 軸承故障特征信號檢測應用

為了檢驗瞬態成分稀疏表示方法的振動分析應用效果，將該方法應用于軸承外圈、內圈、滾動體的局部故障特征提取。

恒定轉速下的軸承外圈、 內圈和滾動體發生故障時，其振動信號表現為周期性的單邊衰減瞬態沖擊響應信號，可用與該沖擊響應成分相匹配的基底稀疏表示，因此可采用本文的方法檢測瞬態成分發生時刻，且其時間間隔的均值為軸承各故障下對應的故障特征周期。

表1 不同信噪比下仿真信號的稀疏表示結果

選取圓柱滾子軸承為試驗對象，軸承型號為NJ208 (TMB)，軸的旋轉速度為1 496 r/min(fr=24.9 Hz)。利用線切割技術分別在軸承外圈、內圈及其中一個滾動體設置了寬度與深度均為0.2 mm的貫通裂痕故障，來模擬軸承局部微弱故障，試驗裝置如圖4所示，該型號軸承的結構參數如表2所示。設置采樣頻率fs=51.2 kHz，采樣點數為5 120，采樣時間t=0.1 s。經計算，軸承外圈、內圈和滾動體對應的理論故障特征頻率分別為142.8,206.3和132.6 Hz。

圖4 試驗臺外觀Fig.4 Rotating machine test rig

3.1 軸承早期外圈故障特征提取

軸承外圈輕微故障時的時域波形如圖5(a)所示。從圖5(a)中不能得到周期循環多沖擊響應成分的發生時刻，因而不能通過時域波形判斷出故障類型。

表2 圓柱滾子軸承NJ208 (TMB)的參數

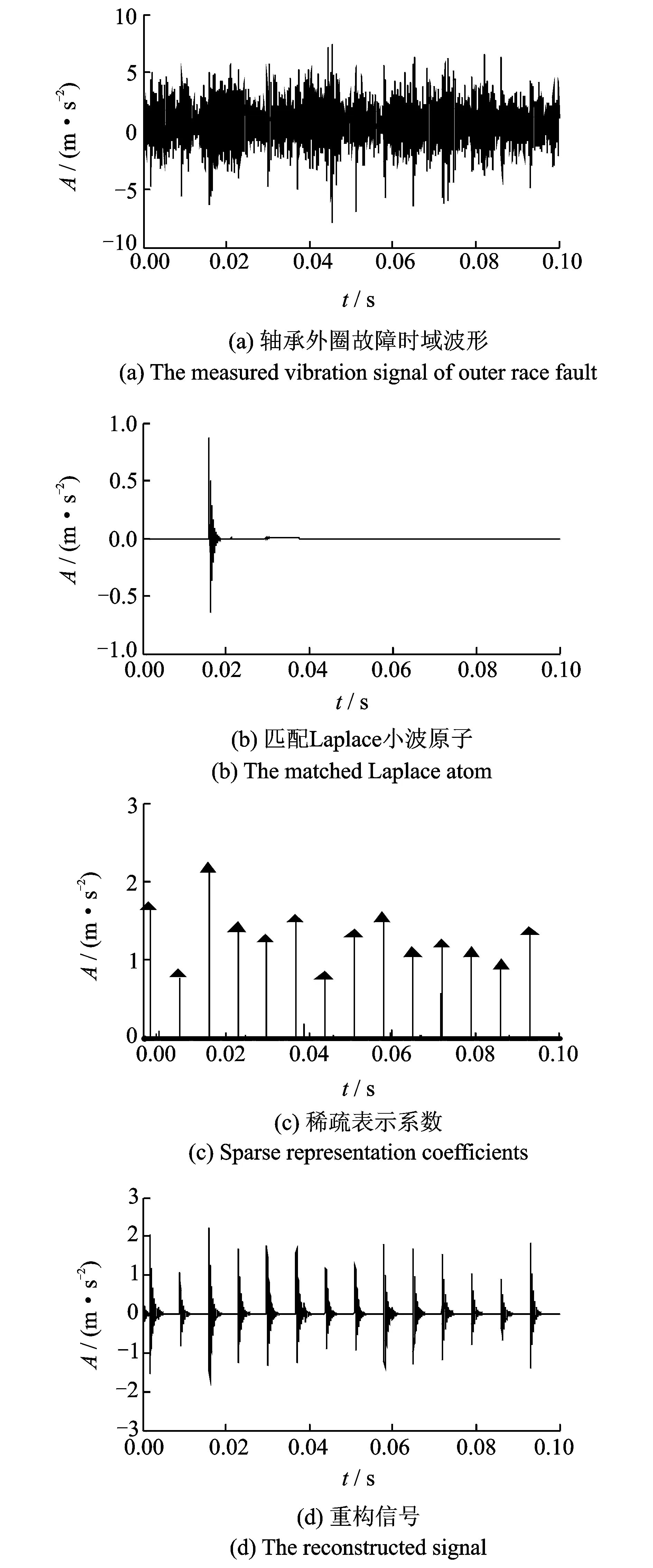
圖5 軸承外圈輕微故障振動信號稀疏表示結果Fig.5 The analysis results of outer race fault by using the proposed method

其次，利用MM算法求解該模型(λ=4，ε=1.5×e-5)，得到稀疏表示系數向量如圖5(c)所示，從圖5(c)中可以直觀得到軸承外圈故障時的沖擊響應時刻，圖5(d)為重構的軸承外圈輕微故障信號。

對圖5(d)中重構信號進行包絡解調分析得包絡譜圖如圖6所示，圖6表明該軸承的故障特征頻率為142.9 Hz，與理論值基本一致。

3.2 軸承早期內圈故障特征提取

圖7(a)為滾動軸承內圈輕微故障對應的時域波形，不能從時域波形中辨識出瞬態成分發生時刻。

圖6 軸承外圈重構信號包絡譜圖Fig.6 The envelope spectrum for the reconstructed signal of the outer race fault

圖7 軸承內圈輕微故障振動信號稀疏表示結果Fig.7 The analysis results of inner race fault by using the proposed method

其次，利用MM算法求解該模型(λ=3.5，ε=1.5×e-5)，圖7(c)為稀疏表示系數向量，圖7(c)中可直觀得到軸承內圈故障時的沖擊響應時刻。圖7(d)為重構的軸承內圈輕微故障信號。

圖7表明該方法能有效識別出沖擊響應時刻點和故障周期。對圖7(d)中重構信號進行包絡解調分析得包絡譜圖如圖8所示，圖8表明該軸承的故障特征頻率為205.9 Hz，與理論值基本一致。

圖8 軸承內圈重構信號包絡譜圖Fig.8 The envelope spectrum for the reconstructed signal of the inner race fault

3.3 軸承早期滾動體故障特征提取

圖9 軸承滾動體故障振動信號稀疏表示結果Fig.9 The analysis results of rolling element fault by using the proposed method

其次，利用MM算法求解該模型(λ=6，ε=1.5×e-5)，稀疏表示系數向量如圖9(c)所示，從圖9(c)中可以直觀得到軸承滾動體故障時的沖擊響應時刻和故障周期。圖9(d)為重構的軸承滾動體故障信號。

對圖9(d)中重構信號進行包絡解調分析得包絡譜圖如圖10所示，圖10表明該軸承的故障特征頻率為131.8 Hz，與理論值基本一致。

圖10 軸承滾動體重構信號包絡譜圖Fig.10 The envelope spectrum for the reconstructed signal of the rolling element fault

4 結 論

以信號稀疏表示理論為基礎，提出了一種小波基下稀疏信號特征提取方法。首先建立了信號瞬態成分稀疏表示模型并提出了模型中兩個關鍵問題；一方面，采用相關濾波法獲得最優小波原子，并張成冗余最優小波基底，解決了基底選擇問題；另一方面，設計了二次嚴格凸函數，并運用MM算法求解模型中的目標函數，解決了方程求解問題。將原始信號中沖擊響應成分轉換為小波基底下的稀疏表示系數，并利用包絡解調分析獲得故障特征頻率，實現了強噪聲背景下弱特征的檢測與提取。

仿真信號研究表明稀疏表示方法對沖擊響應信號的發生時刻具有很強的辨識性，在一定的信噪比內，該方法能準確定位沖擊響應發生時刻，具有較強抑制噪聲干擾的能力。將小波基底下信號稀疏表示特征提取方法應用于軸承故障特征提取，試驗結果表明，該方法能有效提取軸承輕微故障下外圈、內圈和滾動體振動信號中的沖擊響應成分，進而判斷軸承故障類型和故障位置。

[1] 陳向民,于德介,羅潔思.基于信號共振稀疏分解的包絡解調方法及其在軸承故障診斷中的應用[J].振動工程學報,2012,25(6):628—636.

Chen Xiangmin, Yu Dejie, Luo Jiesi. Envelope demodulation method based on resonance-based sparse signal decomposition and its application in roller bearing fault diagnosis[J]. Journal of Vibration Engineering, 2012,25(6):628—636.

[2] Zhu Zhongkui, Yan Ruqiang, Luo Liheng, et al. Detection of signal transients based on wavelet and statistics for machine fault diagnosis[J]. Mechanical Systems and Signal Processing, 2009,23(4):1 076—1 097.

[3] 胡正平,劉文,許成謙,等.局部自適應學習基稀疏約束結合信息優先權選擇擴散的迭代圖像修復算法研究[J].儀器儀表學報,2010,31(3):600—605.

Hu Zhengping, Liu Wen, Xu Chengqian, et al. Iterative image inpainting using sparse constraint with local adaptive learned dictionary and informational priority selected diffusion[J]. Chinese Journal of Scientific Instrument, 2010,31(3):600—605.

[4] Mallat S G, ZHANG Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing. 1993,41(12):3 397—3 415.

[5] Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006,15(12):3 736—3 745.

[6] Mallat S G. A Wavelet Tour of Signal Processing: the Sparse Way[M]. Academic Press, 2008.

[7] Mei Xue, Ling Haibin. Robust visual tracking and vehicle classification via sparse representation[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2011,33(11):2 259—2 272.

[8] Selesnick I. Introduction to sparsity in signal processing[EB/OL]. Connexions Web Site, 2012. http://cnx.org/content/m43545/1.3/.

[9] Cai Gaigai, Chen Xuefeng, He Zhengjia. Sparsity-enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of gearbox[J]. Mechanical Systems and Signal Processing, 2013,41(1):34—53.

[10]Strange G, Nguyen T. Wavelet and Filter Banks[M]. Wellesley-Cambridge Press, 2006.

[11]王詩彬,朱忠奎,王安柱.基于瞬態沖擊響應參數辨識的軸承故障特征檢測[J].振動工程學報,2010,23(4):445—449.

Wang Shibin, Zhu Zhongkui, Wang Anzhu. Bearing fault feature detection based on parameter identification of transient impulse response[J]. Journal of Vibration Engineering, 2010,23(4):445—449.

[12]Figueiredo M A T, Bioucas-Dias J M, Nowak R D. Majorization-minimization algorithms for wavelet -based image restoration[J]. IEEE Transactions on Image Processing, 2007,16(12):2 980—2 991.

[13]Candes E, Tao T. Near optimal signal recovery from random projections: universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006,52(12):5 406—5 425.

[14]Freudinger L C, Lind R, Brenner M J. Correlation filtering of modal dynamics using the Laplace wavelet[A]. Proc. of 16th International Modal Analysis Conference[C]． Santa Barbara, California, 1998:868—877.

[15]Wang Shibin, Huang Weiguo, Zhu Zhongkui. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis[J]. Mechanical Systems and Signal Processing, 2011,25(4):1 299—1 320.

[16]Hunter D R, Lange K. A tutorial on MM algorithms[J]. The American Statistician, 2004,58(1):30—37.

[17]Chen P Y, Selesnick I W. Translation-invariant shrinkage/thresholding of group sparse signals[J]. Signal Processing, 2014,94:476—489.

Wavelet sparse signal feature extraction method and its application in bearing fault diagnosis

FANWei1,LIShuang1,CAIGai-gai1,SHENChang-qing2,HUANGWei-guo1,ZHUZhong-kui1

(1.School of Urban Rail Transportation, Soochow University, Suzhou 215131, China; 2.School of Mechanical and Electrical Engineering, Soochow University, Suzhou 215021, China)

At early stage of bearing fault，the feature components of the original vibration signal are easy to be submerged in strong background noise and thus are hard to be detected． With sparse representation theory, a novel method for transient sparse representation under wavelet basis is proposed. Sparse representation model is firstly constructed, correlation filtering is applied to obtain optimal wavelet atom, thus the optimal redundant wavelet basis, which can best match the transient features of the signal is realized. A designed strictly convex quadratic function is incorporated into Majorization Minimization (MM) algorithm to solve the objective function. With the proposed method, transients hidden in the noisy signal can be converted into sparse coefficients, thus the transients can be detected sparsely. Both the simulation and a real application of rolling bearings with weak fault demonstrate that the weak transients can be effectively obtained through the proposed method.

fault diagnosis; bearing; sparse representaion; MM algorithm; transients

2014-05-15；

2014-10-16

國家自然科學基金資助項目(51375322,51405321);江蘇省自然科學基金資助項目(BK20140339)

TH165.3; TN911.7

A

1004-4523(2015)06-0972-09

10.16385/j.cnki.issn.1004-4523.2015.06.016

樊薇(1990—),女,碩士研究生。電話: 18896512256; E-mail: fanwei.0924@gmail.com

李雙(1976—)，男，博士，副教授。電話: 15298898296; E-mail: lishuang@suda.edu.cn