四個“把握” 提高小學數學課堂教學實效

張 健

(福清市東方紅小學，福建 福清 350300)

四個“把握” 提高小學數學課堂教學實效

張 健

(福清市東方紅小學，福建 福清 350300)

如何提高課堂教學的實效性，成為近幾年教師研究的主要方向。在小學數學教學中如果能把握好學生思維發展的規律，把握好教材的編排思路，把握好操作教學的本質，把握好學生的學情，那么課堂教學實效性將會有一個極大的提升。

思維規律；教材意圖；操作本質

提高課堂教學的有效性已成為近年課堂執教者努力研究的方向。只有提高了課堂教學的有效性，教學才會有張力。把握好以下四個“把握”，將提高教學的有效性。

一、把握學生思維發展規律，讓教學收放自如

學生的思維發展具有一定的階段性，低年級的學生以形象思維為主，到了中高年級，隨著學生思維水平的發展，形象或表象開始逐步讓位于概念，他們漸漸地開始自覺運用概念組成恰當的判斷，并進行合乎邏輯的推理。即使如此，這種抽象的邏輯思維仍然在很大程度上與感性經驗相聯系，也就是說，這種抽象的邏輯思維仍然蘊含著很大成份的形象性。教師如果沒有把握學生的這種思維特質，那么在教學中就難以做到收放自如，深淺有度。下面以某個一年級教學片段略窺一二。

教師在課件中出示了如下一組圖形：

教師讓學生辨別這些圖形是不是長方形，前面7個圖形辨別得都很好，到了最后一個時，

師問：這個是長方形嗎？

生(異口同聲)：不是。

師：仔細觀察思考看看，第8個圖形是不是長方形。

生：不是，那是正方形，四條邊都相等。

師(面向全體學生)：你們也這樣覺得嗎？

生(又齊聲)：是。

無奈，教師只得聯系長方形的特征“對邊相等，四個角都是直角”，告訴學生正方形也是長方形，是一種特殊的長方形。雖然教師講得極其辛苦，但學生似乎并不領情，臉上依然寫滿了疑惑。教師在“正方形是特殊的長方形”這一論斷中糾纏不放，造成課堂教學的低效現象。事實上，小學生認識長方形和正方形要經過兩次不同的階段，第一次是一年級時對常見的平面圖形的初步感知，第二次是三年級的再次認識，是對第一次初步感知的提升。教材做出這樣的編排，是遵循了學生的思維發展規律的，教師應當順應學生的思維發展水平，不必過早地糾結于一些超思維的問題。諸如“正方形是不是長方形”“長方形是不是平行四邊形”“正方體是不是長方體”等類似的問題將會隨著學生思維的發展迎刃而解。只有這樣，教學才會做到深淺有度，自然高效。

二、把握教材的編排思路，讓教學不再偏離正確的軌道

新課程強調教師的個性化教學，鼓勵教師根據實際情況對教材進行深加工，使教材更貼近學生，以發揮教材的教學效益。顯然，這樣的提倡要求教師有更高的教學素質和學科素養，需要教師對教材編寫意圖的諳熟，否則，擅自對教材的“乾坤大挪移”，將使教學陷入“南轅北轍”的境地。請看下面一個《可能性》的教學片段。

(教師出示一個不透明的紙盒)

師：這個盒子里有一些棋子，我們搖一搖，再隨意摸出一個棋子，摸出后再把棋子放回，連續重復幾次，看看每次能摸出什么顏色的球。

(師生共同合作幾次，每次摸出的都是黃色的棋子)

師：你們猜猜看，紙盒里裝的是什么顏色的棋子？

生：黃色的棋子。

生：黃顏色的棋子多，其它顏色的棋子少。

生：只有一個別的顏色的棋子，其它的應該都是黃色的。

生：里面全是黃棋子。

師：那紙盒里到底是什么顏色的棋子呢？我們一起來看一下。(師打開紙盒，里面全是黃棋子，猜對的同學一片歡呼)

師：同學們看，紙盒里全是黃棋時，我們摸到的……

生(齊聲)：一定是黃棋。

……

師：給下面的盒子(如圖)中的小球涂上顏色，使摸出的小球可能是黃色的。

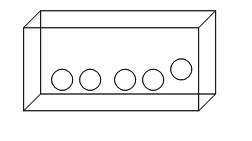
生：把5個球全部涂成黃色。

生：把2個涂成黃色，3個涂成藍色。

生：我覺得黃色的小球應該多一些，涂3個或4個，剩下的1個或2個涂成其它顏色。

那么，學生為什么會有“全部涂成黃色”或者“黃色的小球要多一些”的想法？仔細地審視教師的這一教學過程，不難發現，在“摸棋子”這一環節中，其實學生的想法都是正確的，這正是隨機現象的特征所決定的。可是，當教師打開盒子驗證時，學生所看到的結果卻是唯一的(全部都是黃棋子)，如此一來，猜錯的學生便會有這樣的一種感悟：我的分析是錯誤的。由此，教學就埋下了這樣一種隱患：在分析隨機現象時，大概率事件的發生是絕對的，而小概率事件是不會發生的。

那么，教師為什么要去改變教材的編寫思路？(教材的編寫思路是：先讓學生看到紙盒中全部棋子的顏色，說一說，如果摸一次，二次，三次……，會摸到什么顏色的棋子，然后通過摸棋子驗證猜想，得出結論。)對比之后，我們發現，教材的編寫思路運用于實際教學時較顯平淡，而改編后的教學過程更易激發學生的學習興趣，讓學生更加主動地參與到教學中來，課堂氣氛活躍。可是，教師卻沒有想到，這樣的改變難以為學生建立起正確的隨機觀念，使得教學偏離了正確的軌道。

三、把握操作教學的本質，讓操作不再停留于積累表象

在新課標的指引下，許多教師都對操作教學給予了充分的重視，但許多操作技能教學卻又僅僅是停留在動作的層面上，沒有去關注學生在操作活動過程中是否進行了理性的思考。這樣的操作技能教學是“形而上”的，它沒有觸摸到操作教學的本質，也很難真正進入學生的認知領域，這就導致了學生在“操作”之后，對知識的理解還是淺表性的，思維沒有得到有效的提升，舉一反三自然困難重重。

學生在學習“方程”一單元時，經常會出現這樣的錯誤：

4×8+8X=320
4×8+8X÷8=320÷8
4×8+X=40
32+X=40
X=8

對于學生而言，他們是根據等式的基本性質來進行運算的，那么在等式的左右兩邊同時除以8又為什么錯了呢？蘊含于其中的深層原因又是什么呢？

我們發現，問題的根源在于學生學習《等式的性質》時，教師對操作的教學本質把握不足，許多教師在講解完天平的功能與使用方法之后，就開始組織學生在天平兩邊同時增加(或減少)物品數量，在天平保持平衡的同時，總結出等式性質。正是這種單一的增加(或減少)的操作，使得操作停留在了表象積累的層面，從而失去抽象與提升的契機。因此，教師要從引導學生關注部分轉而引導學生關注整體。如在教學《等式性質》時增加下面的教學環節。(課件出示)

(天平的左邊放2個菠蘿，右邊放6個桃子和4個梨，此時天平保持平衡)

師：現在從天平的左邊拿走1個菠蘿，右邊拿走1個桃子天平還可以平衡嗎？

生：不可以。

師：那左邊拿走1個菠蘿，右邊拿走1個梨可以嗎？

生：不可以。

師：左邊拿走一個，右邊也拿走一個，為什么天平不能保持平衡？

生：因為一個菠蘿的重量不等于一個桃子或一個梨的重量。

生：因為一個菠蘿是左邊的一半，而一個桃子或梨卻不是右邊的一半。

師：那你們覺得應怎樣拿，天平才會保持平衡呢？

生：左邊拿走一個菠蘿，右邊要拿走三個桃子和兩個梨子。

師：還有更深入的想法嗎？

生：左邊去掉一半，右邊也去掉一半，天平就可以保持平衡。

在這樣的一個教學過程中，融入思辨色彩的操作才有了它的應有之義。教師努力地引導學生去關注天平右邊的這個整體，而不是桃子和梨子兩個獨自的個體，學生腦中的表象慢慢地得到抽象與提升，在教師的操作引導下，學生漸漸明確了天平左右兩邊同時去掉的東西必須是“相等的份額”。這樣，學生今后在解類似的方程時就會把目光放在方程兩邊的整體中，從而避免出現上述錯誤。

四、把握學生的學情，讓教學更具針對性

備課不但要備教材，更要備學生，讀懂學生與讀懂教材一樣，都是教學的起點。但事實是，許多教師在教學實踐中更愿意把精力與時間放在鉆研教材上，卻對自己的學生熟視無睹，使得教學失去了應有的針對性，造成了教學的低效現象。

在教學“解比例”時，一位教師教完例題(X∶320=1∶10)之后，引導學生小結“解比例”時，先根據比例的基本性質把比例轉化為方程，再利用學過的知識解方程。之后，便開始了鞏固練習，并請兩名同學上臺板演。板演情況如下：

0.4∶X=1.2∶2 1.25∶0.25=X∶1.6

解：1.2X=0.4×2 解：0.25X=1.25×1.6

1.2X=0.8 0.25 X=2

X≈0.7 X=2÷0.25

X=8

下面的同學做得如何我們不得而知，但僅就板演情況來看，學生的問題已經充分暴露。教師過于關注本課的教學重點，讓學生學會利用比例的基本性質把含有未知數的比例轉化成形如ax=bc的方程，卻忽視了學生在解此類方程時所涉及的計算問題這一教學難點。在這樣的一種方程求解過程中，由于涉及到整數、小數、分數的乘除法兩級混合運算，所以在運算過程中學生還要根據數的特點運用到很多運算技巧。如含有整數、小數、分數的運算中，能約分的要先約分，在含有分數的運算中要把乘除法混合運算轉化為連乘，然后再一次性約分計算等，特別是運算定律的自覺性行為。這些運算技巧雖然學生都已經學過，但卻恰恰是學生在過去的學習中暴露出來的最為欠缺的地方，作為本節課學習的重要基礎，教師對此理應了如指掌，在備課時對學生進行認真解讀，尋找更適合的素材對學生進行有針對性地引導和訓練，使得課堂呈現出一種新中有舊、舊中有新、新舊融合的學習特點，讓教學起到事半功倍的效果。

[1]教育部.義務教育數學課程標準(2011年版)[S].北京：北京師范大學出版社，2012.

[2]張華.新課標背景下關于提高小學數學課堂教學有效性的分析[J].教育教學論壇，2014(14).

2015-05-08

張健(1970- )，女，福建福清人，福清市東方紅小學一級教師。

G623.5

A< class="emphasis_bold">文章編號：1673-9884(2015)06-0074-03

1673-9884(2015)06-0074-03