基于礦區穩定性數值分析的巷道斷面形狀設計★

徐兵 王哲 王志修 王大國

(西南科技大學環境與資源學院，四川綿陽 621010)

隨礦井開采深度增加，“三高一擾動”的復雜條件下，巷道礦壓顯現劇烈，沖擊危險性增大。許多學者對深部高應力巷道設計進行了研究［1-3］，包括理論分析、物理試驗、數值模擬及現場試驗，取得了一些成果，但遠未成熟，特別是在深部沖擊危險性較大的高應力巷道設計中，技術人員大都重點考慮巷道的支護方式及參數，而對巷道斷面的形狀、水平應力等因素考慮較少，往往導致巷道支護成本提高而效果欠佳。對于礦區煤層巷道變形破壞機理研究有過不少報道。張亮等［4］結合數值模擬對復合頂板松軟煤層巷道變形破壞機理進行分析，得到巷道變形破壞原因主要是由于原有支護缺乏主動支護作用。針對復雜圍巖環境條件，陳跟馬等［5］研究了大佛寺煤礦40108工作面巷道變形破壞特征及支護技術，提出了“高強高預應力錨桿(索)+底角錨桿”支護技術控制巷道圍巖穩定性。隨著深井巷道的開挖，巖體可能隨礦井深度的急劇增大產生軟化效益，張志康等［6］研究了不同深度條件下大斷面巷道的圍巖應力、變形及破裂規律，得到600 m的深度即為研究礦區的巖石軟化的臨界深度。目前，研究大都從巷道圍巖應力及變形角度進行分析，探究巷道破壞機理及其處置措施，而針對巷道斷面優化的研究較少，使得高應力巷道設計存在一定的局限。賈陳海［7］對大斷面高地應力煤巷斷面形狀進行了選擇。付強等［8］基于有限差分軟件FLAC3D，研究了巷道截面形狀等對于巷道圍巖變形和壓力分布的影響規律。然而系統地研究不同斷面形狀巷道的應力應變關系及塑性區分布規律，并深入分析了不同側壓力系數的影響的研究較少。本文選取矩形、直墻拱形、梯形、圓形和橢圓形5種斷面形狀的巷道，通過5種典型巷道的應力應變關系及塑性區分布規律，分析不同側壓力系數對圓形和橢圓形斷面巷道的影響，進而對巷道斷面進行優化設計。

1 模型建立

根據礦區巷道中常用的幾種斷面，選取矩形、直墻拱形、梯形、圓形和橢圓形5種斷面形狀的巷道進行分析，其巷道斷面形狀如圖1所示。

本數值模擬以兗州濟寧礦區某工程為背景，根據工程地質條件，本文建立模擬區域的長×寬=80 m×80 m，有限元模擬采用如圖2所示的計算模型。

本模型邊界條件為:側向和底部處的位移受限;模型上表面施加25 MPa的荷載;采用Mohr-Coulomb破壞準則計算圍巖應力應變關系及變形特征、圍巖塑性區分布及不同側壓力系數的影響。其中計算參數如表1所示。

2 結果與討論

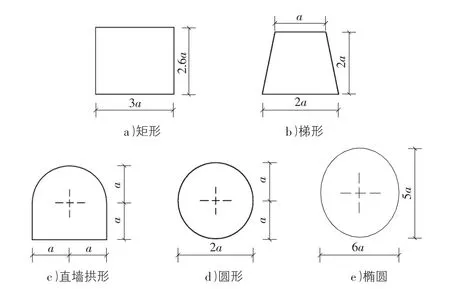
圖1 巷道斷面形狀

圖2 數值計算模型

表1 計算參數

2.1 不同斷面形狀巷道應力應變關系

巷道開挖導致一定范圍內的圍巖應力重新分布，應力從巷道圍巖表面向深部轉移，且分布不均勻，由“等效開挖”［9，10］理論可知，斷面形狀不同，巷道礦壓規律也不完全一致，由此產生的巷道圍巖應力應變關系及塑性區分布也各有不一。

由圖3可知，矩形、梯形斷面巷道主應力差由巷道軸線向兩側肩、底角逐漸收縮，呈現出不均勻性，越靠近圍巖周邊，主應力差的分布越不均勻;遠離圍巖周邊，主應力差的分布逐漸趨向均勻;與矩形、梯形巷道相比，直墻圓拱巷道頂板和幫部邊界均為規則的曲線，主應力差的分布較矩形、梯形巷道明顯改善，均勻性明顯增大;橢圓形、圓形巷道全斷面為曲線，巷道周邊應力分布均勻，且圓形巷道基本處于均壓狀態;圖3表明橢圓形及圓形巷道最小;矩形、梯形巷道主應力差不均勻區域的范圍最大，其次是直墻拱形巷道。

圖3 不同斷面形狀巷道圍巖主應力差及塑性區分布圖（單位：MPa）

2.2 不同斷面形狀對豎向位移的影響

巷道開挖過程中會導致圍巖應力釋放，圍巖應力釋放過程中會沿開挖面產生較大的變形，為了分析研究掌握巷道開挖后圍巖變形特征，本文計算了不同斷面形狀巷道頂板的豎向變形，如圖4所示。

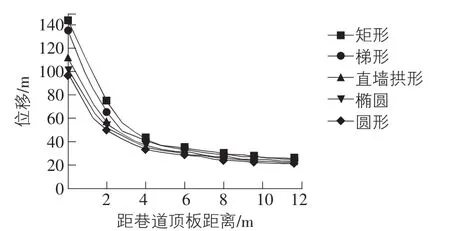
圖4 不同斷面形狀巷道頂板位移

由圖4計算結果可知，隨著距巷道頂板距離的增大，巷道頂板在附加荷載的作用下豎向位移隨之減小，但不同斷面形狀巷道頂板位移存在較大差異。其中圓形斷面形狀的巷道變形最小，而矩形斷面形狀的巷道變形最大，兩種斷面形狀巷道頂板位移最大分別為:144.6 mm和97.6 mm。如圖4所示5種斷面形狀的巷道頂板位移大小順序為矩形＞梯形＞直墻拱形＞橢圓＞圓形，最大位移與最小位移相差32.6%。模擬結果表明巷道邊界線越光滑，巷道頂板位移越小。該結果也印證了圖3中不同斷面形狀巷道圍巖主應力差及塑性區分布結果。圖4同時表明該模擬下不論巷道斷面形狀如何，荷載作用下對巷道頂板位移的影響距離大約為6 m。

2.3 水平應力作用下的斷面形狀優化選取

研究表明深部構造應力作用時，隨著水平應力的不斷提高圍巖能量集聚顯著增長，沖擊地壓的發生幾率增加［11］。通過上文圖4結果可知圓形和橢圓形斷面的巷道位移較其他形狀斷面都要小，因此本文模擬分別取圓形和長軸垂直于地層的橢圓形斷面巷道分析水平應力對巷道穩定性的影響，對巷道斷面選取進行優化。計算巷道斷面面積為9 m2，埋深1 000 m，側壓系數λ分別為0.4，1.0和1.6的巷道主應力。其不同側壓系數條件下兩種斷面巷道主應力分布如圖5～圖7所示。

如圖5所示，當λ=0.4時，在水平方向上的塑性區范圍呈現集中的趨勢，在垂直方向上面的變化范圍不大，塑性區呈扁平狀分布［11］。相比橢圓形巷道，圓形巷道塑性區分布更均勻，橢圓形巷道兩幫塑性區集中。因此，根據塑性區分布分析側壓系數為0.4時圓形巷道較橢圓形巷道要好。

如圖6所示，當λ=1時，巷道圍巖處于等壓狀態，圍巖塑性區在巷道四周基本呈均勻分布，塑性區分布近似圓形。巷道兩幫及頂底板主應力差峰值一致。橢圓形巷道圍巖的主應力峰值略大于圓形巷道。相比之下，橢圓形巷道四周塑性區較圓形巷道要集中。從而側壓系數λ=1的等壓狀態條件下宜選取圓形斷面巷道。

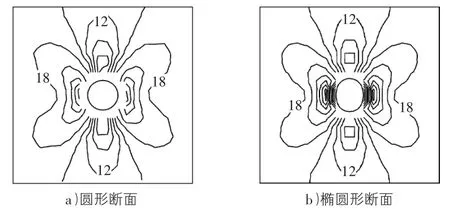
圖5 λ=0.4的圓形/橢圓形斷面巷道主應力分布（單位：MPa）

圖6 λ=1.0的圓形/橢圓形斷面巷道主應力分布（單位：MPa）

圖7 λ=1.6的圓形/橢圓形斷面巷道主應力分布（單位：MPa）

如圖7所示，當λ=1.6時，塑性區在垂直方向的范圍上呈遞增趨勢，在水平方向上的范圍則變化不大，但巷道圍巖塑性區范圍有明顯增大的趨勢，且塑性區呈瘦高型分布。橢圓形巷道圍巖的主應力差峰值比圓形巷道及長軸在垂直方向的橢圓形巷道要小。相比于橢圓形巷道，圓形巷道在頂底兩處塑性區集中。橢圓形巷道塑性區分布更為均勻。

綜上分析可知:當水平應力較小時，巷道圍巖主應力差峰值出現在水平方向，塑性區在水平方向的發育范圍較垂直方向的范圍大，故需盡量減少水平方向上的主應力差及塑性區的分布，降低巷道兩幫的變形量，此時合理的斷面形狀為圓形巷道［11］。當水平應力較大時，巷道圍巖主應力差峰值出現在垂直方向，塑性區在垂直方向的發育范圍較水平方向的范圍大，故需盡量減少垂直方向上的主應力差及塑性區的分布，降低巷道頂底板的變形量，此時合理的斷面形狀為長軸在水平方向的橢圓形巷道。

3 結語

本文基于有限元程序分析了矩形、直墻拱形、梯形、圓形和橢圓形5種斷面形狀的巷道的應力應變關系及塑性區分布規律，并深入分析了不同側壓力系數對圓形和橢圓形巷道的影響。得到了不同斷面形狀巷道圍巖主應力差及塑性區分布;不同斷面形狀的巷道頂板位移大小順序為矩形＞梯形＞直墻拱形＞橢圓＞圓形。模擬結果表明巷道邊界線越光滑，巷道頂板位移越小;通過不同側壓力系數的模擬研究得到當水平應力較大時，合理的斷面形狀為長軸在水平方向的橢圓形巷道;當水平應力較小時，合理的斷面形狀為圓形巷道。

［1］靖洪文，李元海，許國安.深埋巷道圍巖穩定性分析與控制技術研究［J］.巖土力學，2005，26(6):877-888.

［2］常聚才，謝廣祥.深部巖巷底鼓機理及底板超挖錨注回填技術［J］.采礦與安全工程學報，2011，28(3):361-369.

［3］柏建彪，王襄禹，賈明魁，等.深部軟巖巷道支護原理及應用［J］.巖土工程學報，2008，30(5):632-635.

［4］張 亮，方新秋，郭 輝.復合頂板松軟煤層巷道變形破壞機理及合理支護設計［J］.煤礦安全，2012(2):63-66.

［5］陳跟馬，張永濤，賀海鴻，等.復雜圍巖環境下巷道變形破壞特征及支護技術［J］.煤礦安全，2012(10):149-151.

［6］張志康，單仁亮.深井大斷面軟巖巷道變形破裂規律數值模擬［J］.煤礦安全，2012(5):160-163.

［7］賈陳海.大斷面高地應力煤巷斷面形狀選擇的探討［J］.江西煤炭科技，2008(3):72-73.

［8］付 強，趙玉成，何東旭，等.巷道形狀對高應力軟巖巷道變形的影響［J］.煤礦安全，2014(3):194-199.

［9］樊克恭，蔣金泉.弱結構巷道圍巖變形破壞與非均稱控制機理［J］.中國礦業大學學報，2007，36(1):54-59.

［10］李桂臣，張 農，王 成.高地應力巷道斷面形狀優化數值模擬研究［J］.中國礦業大學學報，2010，39(5):652-658.

［11］孟慶彬，韓立軍，喬衛國，等.深部高應力軟巖巷道斷面形狀優化設計數值模擬研究［J］.采礦與安全工程學報，2012，29(5):650-656.