電－熱－力載下BNNTs增強壓電板的非線性動力響應

楊金花，張鵬君

（長沙理工大學土木與建筑學院，長沙 410114）

電－熱－力載下BNNTs增強壓電板的非線性動力響應

楊金花，張鵬君

（長沙理工大學土木與建筑學院，長沙 410114）

研究了電－熱－力載荷作用下硼氮納米管（BNNTs）增強壓電板的非線性動力響應。運用板的非線性應變幾何關系及考慮溫度效應的壓電理論，建立了BNNTs增強壓電板的本構關系。通過變分推導出了結構的非線性動力控制方程。在空間上采用差分法離散，在時間上采用Newton-Newmark方法離散，整個問題采用迭代法進行求解。算例中，詳細討論了電壓、溫度、載荷、體積比以及外激勵頻率等因素對BNNTs增強壓電板非線性動力響應的影響。

非線性動力響應；壓電；板；BNNT；電－熱－力載

硼氮納米管（BNNT）具有類似于碳納米管（CNT）的結構，有很好的力學性能，并且與CNT相比，BNNT具有更好的抗氧化能力及強的壓電特性。另外，BNNT還具有穩定的半導體性能［1－2］。硼氮納米管的這些性質使其似乎可以作為各種納米級的電子和光子設備的替代材料。因此，BNNT越來越廣泛地用作復合結構的加固組分。隨著科技的發展，一種具有壓電性質的新型智能納米復合材料，即用壓電材料作基體而BNNT作增強材料，吸引了科學界的興趣。現有文獻表明，對BNNTs增強壓電結構的研究還很少，且大多討論的是線性靜力問題。因此，有必要對這種結構的非線性動力行為進行更廣泛的研究。

目前大多數研究都局限于討論無BNNT增強的壓電結構的動力行為。隨著微分求積（DQ）逐層建模技術的開發和實現，Zhang等［7］研究了多層壓電復合材料板的自由振動。基于高階剪切板彈性理論和壓電理論，Mao等［8］分析了壓電功能梯度板的非線性動態響應和主動振動控制。基于高階剪切變形板理論，Fakhari等［9］使用有限元分析具有表面粘貼壓電層的功能梯度板在熱、電和力載條件下的非線性固有頻率和頻率響應。為了分析簡支壓電夾層板的自由振動，Benjeddou等［10］提出了一種二維封閉式的解法。Behjat等［11］使用不同的機電載荷下的有限元方法，進行了功能梯度壓電板的非線性靜態分析和自由振動分析。Larbi等［12］給出了壓電復合結構振聲問題的理論公式及有限元解。Xia等［1］研究了熱環境下表面粘貼壓電纖維增強復合材料板的非線性振動及動態響應。Dash等［14］分析了內埋或表面粘結壓電層的復合材料層合板的非線性自由振動特性。Wang等［15］使用有限元模型，研究了壓電復合材料板的負速度反饋控制的動力穩定。Liew等［16］使用一種有效的無網格方法，討論了帶壓電傳感器或驅動器的復合材料層合板的主動控制。Zhang等［17］提出了由1－3個纖維增強的壓電復合層合板及正交復合層合板的結構振動控制分析方程。Yang等［18］研究了復合壓電殼的動力不穩定性。Saviz等［19］給出了簡支壓電層合圓柱殼層的動力分析。Ying等［20］分析了壓電厚殼在邊界隨機激發平面應變條件下的隨機響應。D'Ottavio等［21］研究了內埋壓電材料的多層殼的自由振動問題。以上研究中均沒有考慮BNNT增強壓電結構。

近年來出現了一些對于BNNTs增強壓電結構靜力屈曲問題的研究。Salehi-Khojin等［22］研究了電－熱－力載下PVDF彈性介質中BNNT的屈曲問題，Mosallaie Barzoki等［23］研究了具有彈性核心的BNNTs增強的PVDF圓柱殼的扭轉屈曲。在另一項研究中，Mosallaie Barzoki等［24］研究了BNNT增強內埋壓電殼的非線性屈曲。使用基于非局部圓柱壓電連續殼理論的虛位移原理，Ghorbanpour Arani等［25］討論了電－熱－力負荷條件下內埋彈性介質中雙壁硼氮納米管的軸向屈曲。到目前為止，BNNTs增強壓電板的非線性動力研究尚未見報道。

出于這種考慮，本文我們研究電－熱－力載下BNNTs增強壓電板的非線性動力響應。空間上使用有限差分法，時間上采用Newton-Newmark方法，整個問題通過迭代求解。討論了電壓，溫度，力載及體積比等對BNNTs增強壓電板的非線性動力響應的影響。

1 基本方程

圖1為一BNNTs增強壓電板，板的長度為a，寬度為b，厚度為h，板的密度為ρ0。坐標系o－xyz置于板的中面（z＝0），壓電板受有橫向動載荷q，施加電壓為V及溫度升高ΔT。

圖1 BNNTs增強壓電板幾何示意圖Fig.1 Geometry of piezoelectric plate reinforced with BNNTs

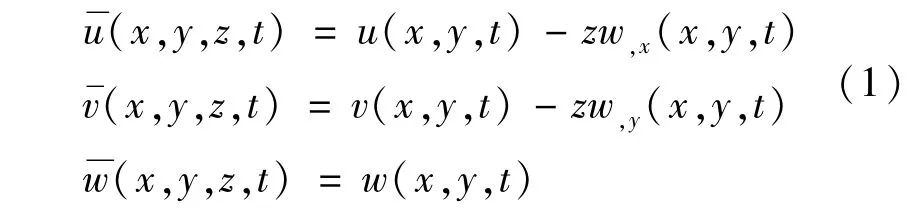
下標（，）表示對坐標變量求偏導。

其非線性應變－位移關系可表示為

式中，εx，εy，εxy為殼中面上相應點的應變，κx，κy，κxy分別為殼中面上相應點的曲率和扭率改變量，且

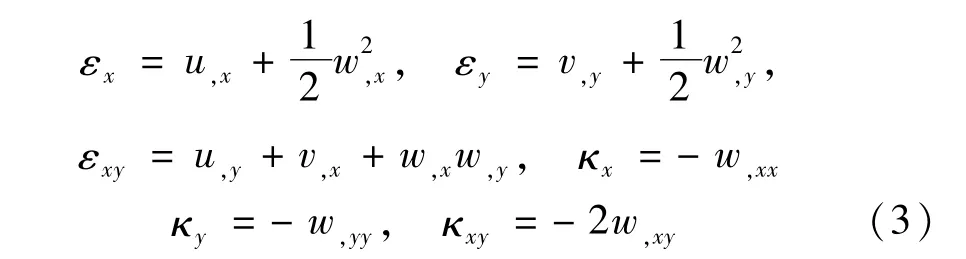
對電－熱－力載荷作用下的壓電結構而言，本構關系可寫為［23，29－30］

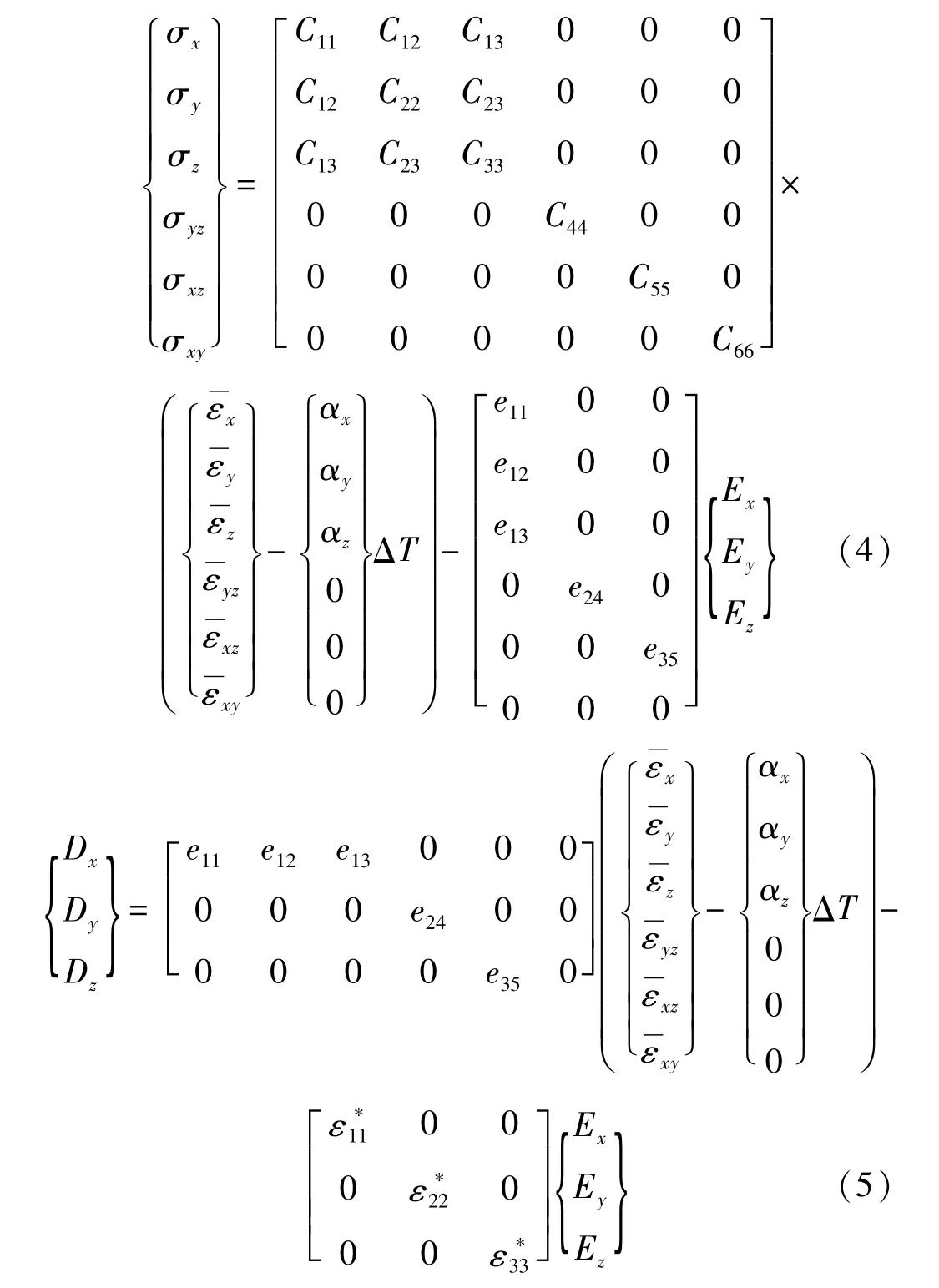
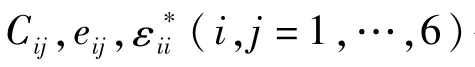
一般而言，鵬氮納米管（BNNTs）有兩種對稱結構，即Z字形的和扶手椅形狀的。Z字形管具有縱向壓電響應，而扶手椅形管存在與扭轉耦合的電偶極矩，因此本文采用前者。智能壓電板由兩種材料組成，基體材料為PVDF，增強材料為BNNTs，結構整體的材料常數可用'XY（或YX）［27－28］矩形模型計算得到，其表達式為

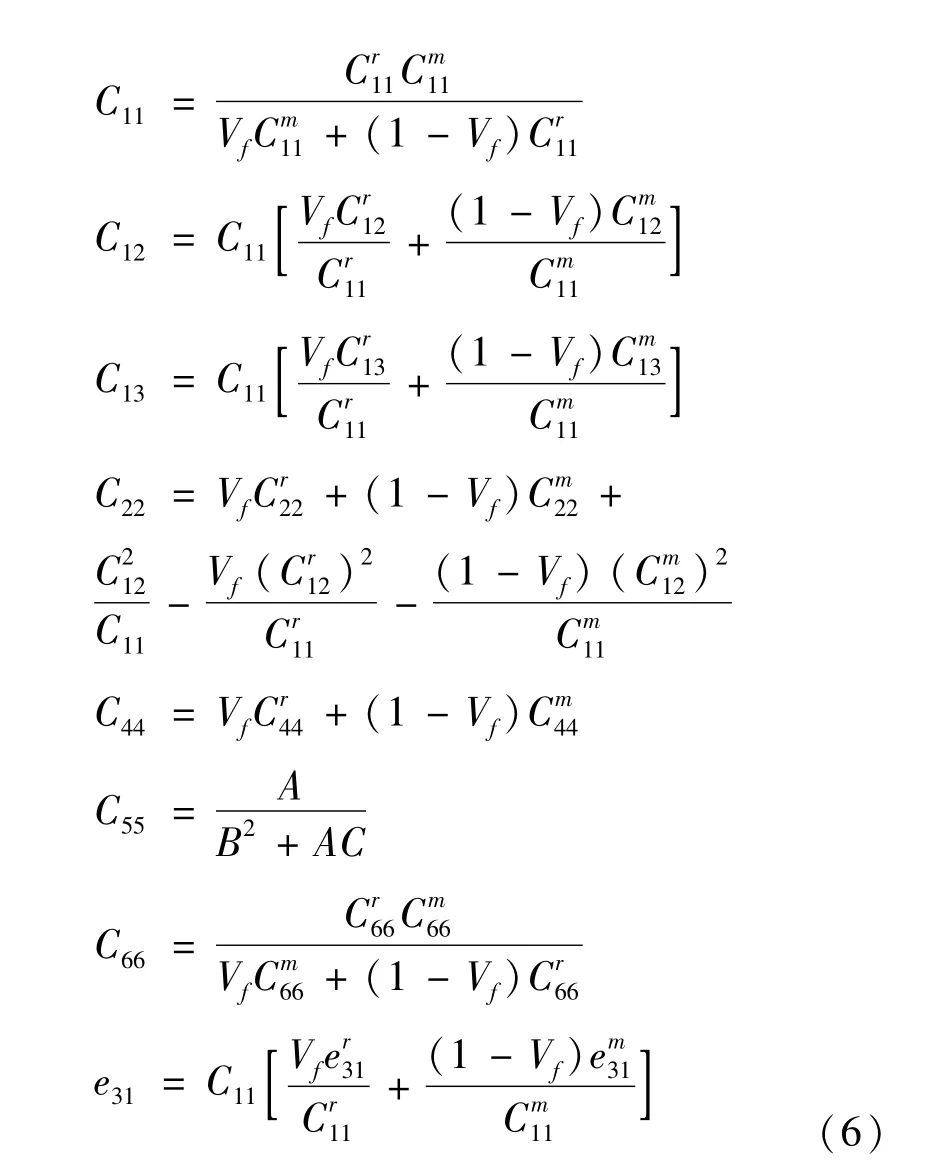
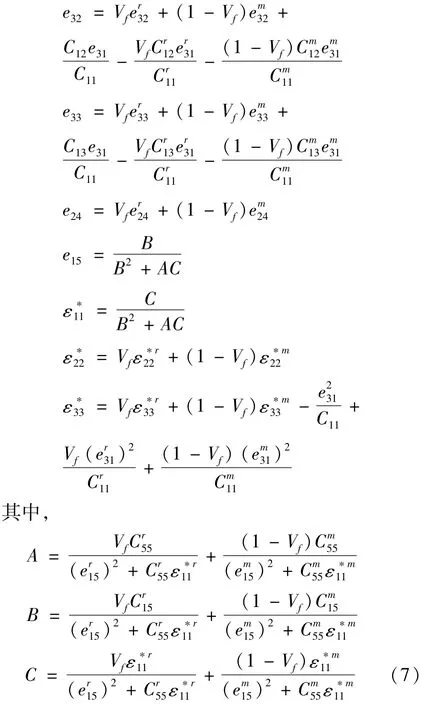
上標r，m分別指增強及基體材料，Vf為增強材料（BNNTs）在基體材料（PVDF）中所占的體積比。BNNTs增強壓電板的總能量Π可寫為

式中，K代表動能，U為應變能，Γ為外載所做的功。應變能為

考慮采用的是z字形結構的BNNTs，則有

運用瑞茲變分原理δΠ＝0，可得BNNTs增強壓電板的非線性動力控制方程為

則電－熱－力載下BNNTs增強壓電板的無量綱動力控制方程可寫為

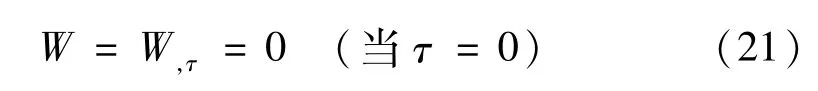
2 求解方法

為了尋求滿足初始條件（21）及邊界條件（20）的非線性運動微分方程組（19）的解，我們將無量綱位移函數W，V，U在空間和時域內離散，以求其近似解。

在空間上采用差分法離散。對于線性項的處理，型如U，ξ，V，η，U，ξξ，W，ξ，W，ξξ，W，ξξξξ等各階偏導數項，以W，ξξ為例，采用如下的差分格式：

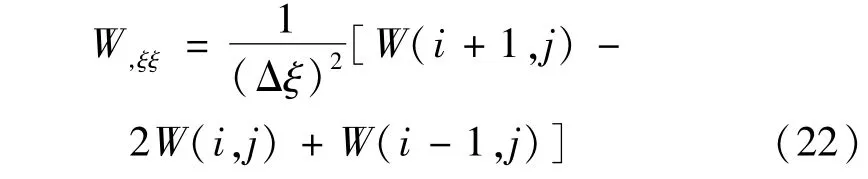
對照差分格式，可容易的求得控制方程中其余各線性項的各階偏導數的差分表達式。

在時間上將外載荷的作用時間τ等分為n等份，記每一等份為Δτ，整個問題采用迭代法求解。在任一迭代步j中，控制方程和定解條件中的非線性項被線性化，且寫為如下的形式［31］

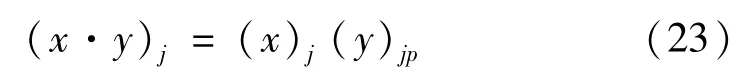
式中，（y）jp是前二次迭代值的均值。對于初始迭代步，可以應用二次外推法求解，即

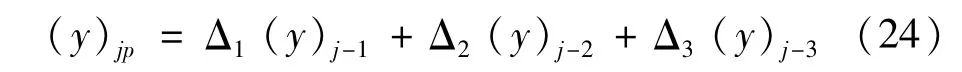
對于不同的迭代步，系數Δ1，Δ2及Δ3可以分別取如下的數值：

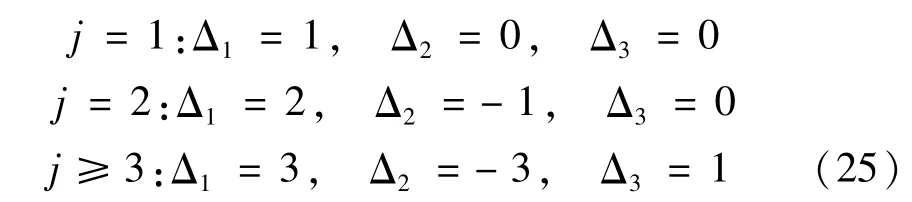
對于三次非線性項的處理方法與二次非線性項的處理方法相同。

同時，采用Newmark方法，將控制方程中對時間變量的偏導數項如W，ττ在時間上離散。將外載荷的作用時間τ等分為n等份，記每一等份為Δτ＝τ／n，則在網格點j的加速度項W，ττ可表示為

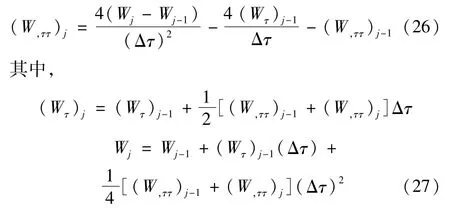
經過差分處理和線性化以后，非線性微分控制方程由最初的偏微分方程組轉化為差分格式的線性代數方程組。聯立求解此方程組，對每一時間步采用迭代法求解，迭代過程持續到相鄰兩次所得計算結果的誤差小于某一給定精度（本文為10－12），在第j步取得收斂解后，該迭代步終止，再進行第j+1步的計算。

3 數值計算與討論

下面算例中討論了電－熱－力載下BNNTs增強壓電板的非線性動力響應。壓電板的四邊簡支，幾何尺寸為a／h＝10，b／h＝10，壓電板基體材料為PVDF，增強材料為BNNT，材料常數如表1所示。橫向動載荷取為

式中，

為外激勵幅值，ω為外激勵頻率（圖6除外，各算例中ω＝1）。各圖中垂直坐標W

0

為板的無量綱中心撓度，水平坐標τ為無量綱時間。

表1 材料常數Tab.1 Mechanical，electrical and thermal properties of PVDF and BNNT

電－熱－力載荷下BNNT所占體積比Vf對板中點非線性動力響應的影響如圖2（a）所示。本算例中，電壓V＝25 v，溫度ΔT＝50 K，外激勵幅值＝0.1。從圖中可看出隨著BNNT在基體中所占體積比Vf的增加，板中點的動力響應幅值減小。這是因為體積比Vf的增加會使得結構的整體剛度變大，因而動力響應幅值會減小。另外，圖2（b）還給出了當Vf＝0.6時本文的計算結果和用Ansys軟件模擬分析的結果，此圖中外激勵幅值、電壓、溫度與圖2（a）中的相同。從圖2（b）可見，本文的計算結果與用Ansys模擬分析所得的結果吻合較好，說明本文的力學模型和分析方法是合理的。

圖3給出了正負電壓對不同體積比下BNNT增強壓電板非線性動力響應的影響。圖中溫度ΔT＝0，外激勵幅值＝0.1。從圖中可看出在硼氮納米管增強壓電板兩端施加負電壓會使結構的響應幅值減小。這是由于施加負電壓會使硼氮納米管沿x方向極化，產生收縮，因而使得結構更加緊湊堅固，結構的剛度增大，故結構的非線性動力響應幅值減小。圖中同時也給出了正電壓對BNNT增強壓電板非線性動力響應的影響，從圖中可看出，正電壓會使BNNT增強壓電板非線性動力響應幅值增大。另外，比較圖3（a）、（b）可知，隨著硼氮納米管所占體積比Vf的增大，正電壓對壓電板非線性動力響應的影響要減弱，而負電壓的影響要增強，圖中難以看出此變化規律，為此將其列于表2所示。

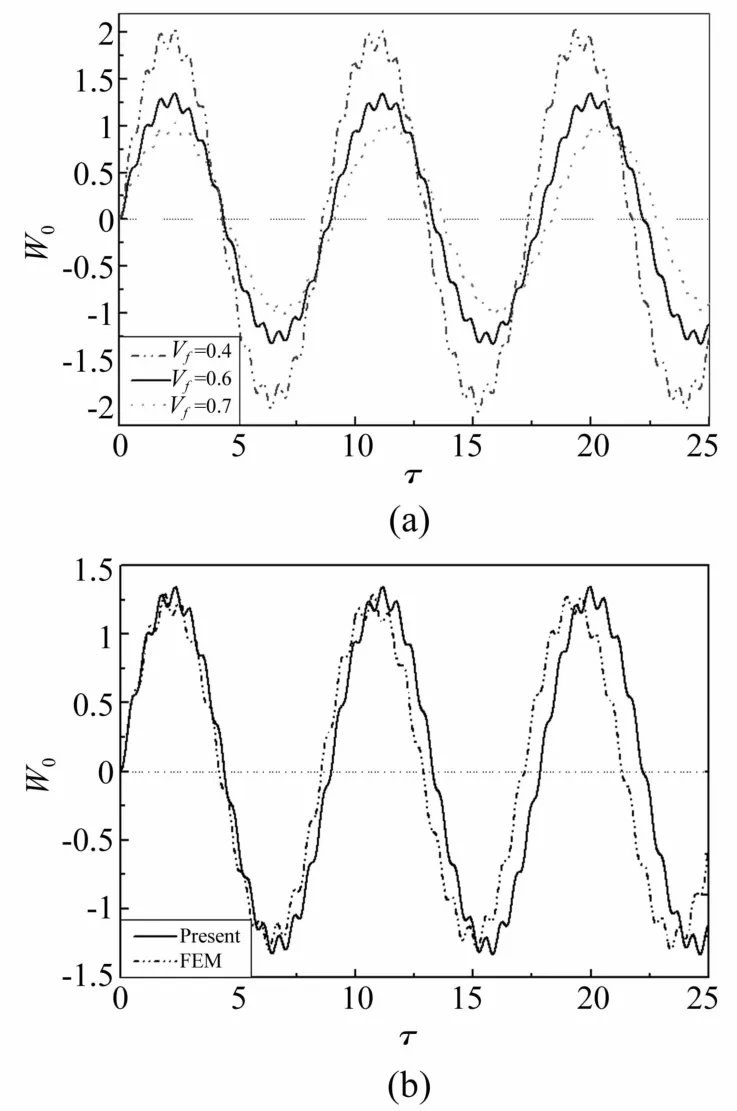
圖2 體積比Vf對BNNT增強壓電板非線性動力響應的影響Fig.2 Effect of volume fraction Vfon the nonlinear dynamic response of BNNT-reinforced piezoelectric plate

圖3 電壓對BNNT增強壓電板非線性動力響應的影響Fig.3 Effect of applied voltage on the nonlinear dynamic response of BNNT-reinforced piezoelectric plate

表2 電壓對BNNT增強壓電板非線性動力響應的影響Tab.2 Effect of app lied voltage on the nonlinear dynam icresponse of BNNT-reinforced piezoelectric p late

溫度對BNNT增強壓電板非線性動力響應的影響如圖4所示。圖中硼氮納米管所占體積比Vf分別為0.6和0.8，電壓V＝0，外激勵幅值＝0.1。從圖中可看出，壓電板非線性動力響應幅值隨著溫度的升高而變大。另外，比較圖3（a）與圖3（b）可知，隨著硼氮納米管所占體積比Vf的增大，溫度對壓電板非線性動力響應的影響要減小（參見表3）。

圖4 溫度對BNNT增強壓電板非線性動力響應的影響Fig.4 Effect of temperature on the nonlinear dynamic response of BNNT-reinforced piezoelectric plate

表3 溫度對BNNT增強壓電板非線性動力響應的影響Tab.3 Effect of tem perature on the nonlinear dynam ic response of BNNT-reinforced piezoelectric plate

圖5給出了橫向動載荷幅值對BNNT增強壓電板非線性動力響應的影響。圖中體積比Vf＝0.6，溫度ΔT＝50 K，電壓V＝25 v。由圖5可知，當壓電板承受的外載荷幅值越大，其在振動過程中達到的幅值也越大。同樣，比較圖3（a）與圖3（b）可知，荷載對壓電板非線性動力響應的影響隨著Vf的增大而減小（參見表4）。

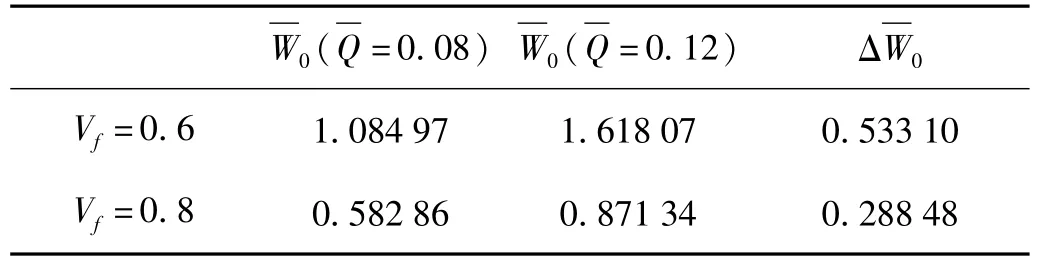
表4 載荷對BNNT增強壓電板非線性動力響應的影響Tab.4 Effect ofmechanical load on the nonlinear dynam ic response of BNNT-reinforced piezoelectric plate

圖5 外載荷對BNNT增強壓電板非線性動力響應的影響Fig.5 Effect ofmechanical load on the nonlinear dynamic response of BNNT-reinforced piezoelectric plate

圖6給出了外激勵頻率對BNNT增強壓電板非線性動力響應的影響。圖中體積比Vf＝0.6，溫度ΔT＝50 K，電壓V＝25 v，外激勵幅值＝0.1。從圖中可看出，壓電板非線性動力響應幅值隨著外激勵頻率ω的增加而減小。比較圖3（a）與圖3（b）可知，隨著體積比Vf的增大，外激勵頻率對壓電板非線性動力響應的影響也減小（參見表5）。

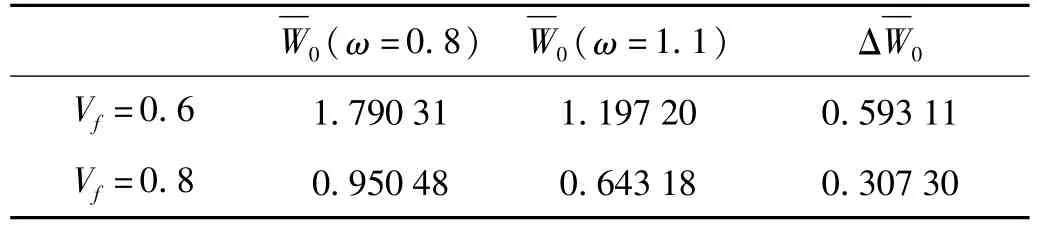
表5 外激勵頻率對BNNT增強壓電板非線性動力響應的影響Tab.5 Effect of external excitation frequency on the nonlinear dynam ic response of BNNT-reinforced piezoelectric p late

圖6 外激勵頻率對BNNT增強壓電板非線性動力響應的影響Fig.6 Effect of external excitation frequency on the nonlinear dynamic response of BNNT-reinforced piezoelectric plate

4 結 論

本文建立了電－熱－力載荷作用下BNNTs增強壓電板的非線性動力響應控制方程。研究結果表明電壓、溫度、荷載、體積比以及外激勵頻率等因素對BNNTs增強壓電板非線性動力響應有著重要的影響。結果如下：

（1）在BNNTs兩端施加正或負電壓可使壓電板非線性動力響應幅值增加或減小；

（2）BNNTs增強壓電板非線性動力響應幅值隨著外載荷及溫度的增加而增大；隨著外激勵頻率及硼氮納米管所占體積比的增加而減小。

（3）隨著硼氮納米管所占體積比Vf的增大，正電壓、溫度、荷載以及外激勵頻率等因素對壓電板非線性動力響應的影響會減小。

［1］Chen CW，Lee M H，Clark S J，Band gap modification of single-walled carbon nanotube and boron nitride nanotube under a transverse electric field［J］.Nanotechnology，2004，15：1837.

［2］Bansal N P，Hurst JB，Choi SR，Boron nitride nanotubereinforced glass composites［J］.J Am Ceram Soc，2006，89：388.

［3］Chen Y，Zou J，Campbell S J，et al，Boron Nitride nanotubes：Pronounced Resistance to Oxidation，Appl.Phys.Lett.84（2004）2430－2432.

［4］Suryavanshi A P，Yu M F，Wen J，etal.Elasticmodulus and resonance behavior of boron nitride nanotubes［J］.App. Phys.Lett.，2004，84：2527－2529.

［5］Terrones M，Romo-Herrera JM，Cruz-Silva E，etal.Mu?oz-Sandoval，J.J.Velázquez-Salazar，H.Terrones，Y.Bando，D.Golberg，Pure and Doped Boron Nitride Nanotubes，Mater.Today，2007，10：30－38.

［6］Zhi C，Bando Y，Tang C，et al.Characteristics of boron nitride nanotube-polyaniline composites［J］.Angew Chem Int Ed，2005，44：7929.

［7］Zhang Zan，Feng C，Liew K M.Three-dimensional vibration analysis of multilayered piezoelectric composite plate［J］.International Journal of Engineering Science，2006，44（7）：397－408.

［8］Mao Yi-qi，Fu Yi-ming，Nonlinear dynamic response and active vibration control for piezoelectric functionally graded plate［J］.Journal of Sound and Vibration，2010，329（11）：2015－2028.

［9］Fakhari V，Ohadi A，Yousefian P.Nonlinear free and forced vibration behavior of functionally graded plate with piezoelectric layers in thermal environment［J］.Composite Structures，2011，93（9）：2310－2321.

［10］Benjeddou A，DeüJ F.A two-dimensional closed-form solution for the free-vibrations analysis of piezoelectric sandwich plates［J］.International Journal of Solids and Structures，2002，39（6）：1463－1486.

［11］Behjat B，Khoshravan M R.Geometrically nonlinear static and free vibration analysis of functionally graded piezoelectric plates［J］.Composite Structures，2012，94（3）：874－882.

［12］LarbiW，DeüJF，Ohayon R，Finite element formulation of smart piezoelectric composite plates coupled with acoustic fluid［J］Composite Structures，2012，94（2）：501－509.

［13］Xia Xian-kun，Shen Hui-shen.Nonlinear vibration and dynamic response of FGM plates with piezoelectric fiber reinforced composite actuators［J］.Composite Structures，2009，90（2）：254－262.

［14］Dash P，Singh B N.Nonlinear free vibration of piezoelectric laminated composite plate［J］.Finite Elements in Analysis and Design，2009，45（10）：686－694.

［15］Wang SY，Quek S T，Ang K K，Dynamic stability analysis of finite element modeling of piezoelectric composite plates ［J］.International Journal of Solids and Structures，2004，41 （3－4）：745－764.

［16］Liew K M，He X Q，Tan M J，et al.Dynamic analysis of laminated composite plates with piezoelectric sensor／actuator patches using the FSDTmesh-freemethod［J］.International Journal of Mechanical Sciences，2004，46（3）：411－431.

［17］Zhang H Y，Shen Y P.Vibration suppression of laminated plates with 1－3 piezoelectric fiber-reinforced composite layers equipped with interdigitated electrodes［J］.Composite Structures，2007，79（2）：220－228.

［18］Yang X M，Shen Y P.Dynamic instability of laminated piezoelectric shells［J］International Journal of Solids and Structures，2001，38：2291－2303.

［19］Saviz M R，Mohammadpourfard M.Dynamic analysis of a laminated cylindrical shell with piezoelectric layers under dynamic loads［J］.Finite Elements in Analysis and Design，2010，46：770－781.

［20］Ying ZG，Zhu X Q.Response analysis of piezoelectric shells in plane strain under random excitations［J］.Acta Mechanica Solida Sinica，2009，22：152－160.

［21］D'Ottavio M，Ballhause D，Kr?plin B，et al.Closed-form solutions for the free-vibration problem of multilayered piezoelectric shells［J］.Computers＆Structures，2006，84：1506－1518.

［22］Salehi-Khojin A，Jalili N.Buckling ofboronnitridenanotube reinforced piezoelectric polymeric composites subject to combined electro-thermo-mechanical loadings［J］.Compos Sci Technol，2008，68：1489－501.

［23］Mosallaie Barzoki A A，Ghorbanpour Arani A，Kolahchi R，et al.Electro-thermo-mechanical torsional buckling of a piezoelectric polymeric cylindrical shell reinforced by DWBNNTswith an elastic core［J］.Appl.Math.Model，2012，36：2977－2989.

［24］Mosallaie Barzoki A A，Ghorbanpour Arani A，Kolahchi R，et al.Nonlinear buckling response of embedded piezoelectric cylindrical shell reinforced with BNNT under electro-thermomechanical loadings using HDQM［J］.Composites Part B：Engineering，2013，44（1）：722－727.

［25］Ghorbanpour Arani A，Amir S，Shajari A R，et al.Electrothermo-mechanical buckling of DWBNNTs embedded in bundle of CNTs using nonlocal piezoelasticity cylindrical shell theory［J］.Composites Part B：Engineering，2012，43：195 －203.

［26］Sai N，Mele E J.Microscopic theory for nanotube piezoelectricity［J］.Phys Rev B，2003，68：1405.

［27］Tan P，Tong L，Steven G P.A 3D modeling technique for predicting the linear elastic properties of opened-packing woven fabric unit cell［J］.Composite Structures，1997，38：261－271.

［28］Tan P，Tong L.Micro-electromechanics models for piezoelectric-fiber-reinforced composite materials［J］.Compos.Sci.Technol，2001，61：759－769.

［29］Yang J，Xiang H J.Thermo-electro-mechanical characteristics of functionally graded piezoelectric actuators［J］.Smart Mater.Struct，2007，16：784－797.

［30］Yang J，Kitipornchai S，Liew K M.Nonlinear analysis of thermo-electro-mechanical behavior of shear deformable FGM plates with piezoelectric actuators［J］.Inter.J.Numeri.Methods Eng，2004，59：1605－1632.

［31］傅衣銘，結構非線性動力分析［M］.廣州：暨南大學出版社，1997.

Nonlinear dynam ic response of a piezoelectric p late reinforced w ith BNNTs under electro-thermo-mechanical loadings

YANG Jin-hua，ZHANG Peng-jun
（School of Civil Engineering and Architecture，Changsha University of Science＆Technology，Changsha 410114，China）

The nonlinear dynamic response of a piezoelectric plate reinforced with boron nitride nanotubes （BNNTs）under electro-thermo-mechanical loadings was studied.Using nonlinear strains based on the plate theory and the piezoelectric theory considering thermal effects，the constitutive relations of the piezoelectric plate reinforced with BNNTs were established.Then，the dynamic governing equations of the structure were derived with the variational principle.Using the differencemethod in space and Newton-Newmark method in time，thewhole problem was solved with the iteration method.In numerical examples，the effects of voltage，temperature，mechanical load，volume ratio and external excitation frequency on the nonlinear dynamic response of the piezoelectric plate reinforced with BNNTs were discussed.

nonlinear dynamic response；piezoelectric；plate；BNNT；electro-thermo-mechanical loadings

O341

A

10.13465／j.cnki.jvs.2015.21.026

國家自然科學基金（11102028）

2015－04－27 修改稿收到日期：2015－07－15

楊金花女，博士，副教授，1974年生