從優秀走向優雅

優秀的教師會不斷地發展自己的教學技能，而當技能“進化”到技藝時，教師及課堂就從優秀走向了優雅。為此，許多教師在不斷地探索著。筆者也嘗試以“321實效課堂”為載體，試圖立足于傳統而后沖破其思維的禁錮，讓課堂教學緊貼本位，以求得實效，從優秀走向高雅。

一、“321實效課堂”的基本理念

“321實效課堂”以“自主學習、互助探究、展示交流、教師點撥”為主線，構建課堂新秩序，強調課堂要從思維出發，發展學生思維能力。

1.理念“321”。三類優先：教育優先于教學，學優先于教，過程優先于結果。兩個目標：做出色的自己，做重要的他人。一種體驗：點燃他人，照亮自己，成就自己。

2.學法“321”。三自：自讀，自探，自省。二議：議亮點，議盲點。一點撥：教師點撥。

3.教法“321”。三講：想一想能懂的，慎講；跳一跳能懂的，精講；議一議不懂的，深講。兩種能力：運算能力，推理能力。一回頭：反思。

4.學生“321”。三類問與不問：想一想能懂的，不問；跳一跳能懂的，慎問；議一議不懂的，必問。兩種“1+1”組合：一幫一組合，交朋友；一追一組合，找對手。一種信念：永不放棄。

5.教師“321”。三種視角：跳出教育看教育；跳出教學看教學；跳出學科看學科。兩種能力：嫻熟的駕馭課堂能力，良好的處理偶發事件能力。一種境界：向學生學習。

6.試卷講評“321”。三處講起：從多數人的錯誤講起，從刻骨銘心的錯誤講起，從不可容忍的錯誤講起。兩次等待：讓學生再做錯題，先做后議。一個錯題本：讓學生準備一本錯題本。

網絡上有一個名為“35太難了”的教學視頻，內容是一位小朋友在父母的逼問下背“1×5～6×5”的乘法口訣，起初總把3×5背成35，后來連其他當初能背出的口訣也背錯了，這位小朋友哭訴“35太難了”的聲音令人揪心。我們不禁要問：“35”真有這么難嗎？是誰使“35”變得這么難的？“35太難了”折射出怎樣的教育理念和教育現狀呢？

其實，真正的教學不是背誦3×5，而是3×5為什么是15，又為什么不是35？回顧自己多年的教學經歷，真是汗顏——我干過像“35太難了”這樣的事有太多回了，真的需要改變課堂教學了。其實，課改不是很高深的東西。針對同樣的教學內容，教師面對不同學生有不同的處理方法，面對相同學生的不同學習階段也有不同的處理方法，這就是課改。從這個層面上看，每位教師都是課改的踐行者。通俗地說，課改就是改課。改課不是對過去的否定，而是基于對傳統繼承后的不斷修正、完善與發展，是為實現既定課程目標而做出思維方法的選擇。

二、“321實效課堂”應把握的三個常規

當今教師承載的使命遠不僅僅是傳授知識這么簡單，一個有智慧的教師應該有“教育優先于教學”的職業理念，讓自己的職業行為由學科教學進入學科教育。從“學科教學”到“學科教育”是情感的滲入，是理念的跨越。教而不育，僅及皮毛，師生難以交心，“親其師信其道”便要大打折扣。更有甚者，教師缺乏與學生的心靈溝通，凸顯“情感漠視”，從而導致了教與學的雙向缺失。因而要做到“321實效課堂”應把握的三個常規。

1.變管為理。教師是教學管理者，“管”是繞不開的一份責任。“管”的最高境界是“理”。

（1）理解學生的“負重”。做學生不容易，做個好學生更非易事。筆者經常回憶起自己做學生時的“坎坷”經歷，并以此給學生借鑒和參考。

（2）理順教學過程中的各個環節，使之精細化。教師應該知道自己和學生什么時候該做什么，怎么做；什么情況下先做什么，后做什么。比如錯題本格式，筆者就推廣黎瑾同學的做法：一是錯題分析，包括錯誤答案及誤區回顧等；二是共同分享，包括正確思路及有效拓展等。我們把它稱為“黎瑾模式”。

（3）理性對待學生的學習困難。教師要本著“包容個性、尊重差異、相對成長”的原則，爭做學生的“貼心人”。必須依靠學生，不斷細化并完善每一個教學環節，關愛學生，讓他們體驗到學習的快樂。

2.變督為導。督為督促、督查，有催促、問責之意，教師用之無可非議。但若用得單一、頻繁、不當，往往收效甚微，直至無效。

（1）指導。要轉變思路，變學后督導為學前指導，幫助學生制定學習方案，明確學習策略，避免一些學習障礙。

（2）疏導。“321實效課堂”實施初始階段，由于學生固有的行為習慣需要改變，新的學習習慣還未形成，不少學生還不適應。此時，教師應多一些肯定和鼓勵，少一些批評和指責，盡己之力，做學生學習的向導，找出不足，不斷反思，化解學生疑難。

（3）誘導。教師要讓學生相信自己的能力，同時與學生一起設置階段性學習目標，由易到難，層層深入，通過情景誘導、問題誘導、方法誘導、目標誘導等，不斷激發學生的學習熱情。比如在課堂展示交流環節，鼓勵學生“不拘小節”：站著、坐著、吼著等均可為之，為的是要充分表達自己的觀點，宣泄自己的情感，在思維的激烈碰撞中達成一致。

3.變懲為治。懲有懲罰、懲戒、懲處之意。有人認為，懲是為了治，嚴懲更是為了好治，更有甚者把懲當成治。當教育已經進入懲的階段時，就意味著以前的管理失效；而當懲而無效時，教育者則無路可退，可基本認定為管理失敗。筆者認為治才是糾錯、改正乃至改進之道。在筆者參與制定的課堂評價方案中，只有加分項，沒有扣分項，就是充分運用教育等待，實施以治為本的教育策略。

（1）自治。自治需要通過自省來糾正偏離目標的行為，我要求學生每天問自己幾個問題——今天，學習互動得好嗎？還有什么沒有解決的問題？明天，怎樣去做得更好？

（2）互治。在課堂互動時，由學科小組長召集其成員就存在的問題進行充分的梳理、分析、討論，直至解決。另外，筆者要求每位學生處一位最交心的朋友，找一位理想的對手，讓朋友成為學習、生活的好伙伴，讓對手成為學習、生活的好標桿。

（3）救治。針對某個學生存在的學習障礙，安排本組成績好的學生進行一對一輔導，同時教師也適時參與其中，給予其適當的幫助。

三、“321實效課堂”的基本要求

“321實效課堂”是以“自主學習、互助探究、展示交流、教師點撥”為主線構建課堂新秩序，強調課堂要從思維出發。下面以“圓與圓的位置關系”為例做具體介紹。

1.自主學習。自主學習基本要求是：在上新課前閱讀課本相關內容，獨立完成課本習題及課前案，對不懂的地方做出標注；在課堂開始時獨立完成課中案、課前案的基本內容。例如，在教學“圓與圓的位置關系”時，教師讓學生回顧下列知識：

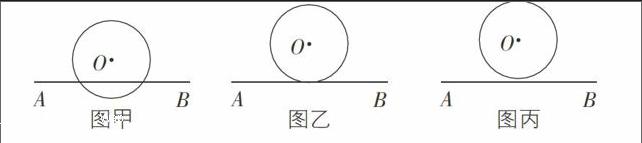
（1）直線AB與⊙O的位置關系如下圖所示：

①它們的位置關系是：圖甲 ，圖乙 ，圖丙 。

②它們都是軸對稱圖形嗎？如是，請分別在圖中畫出它們的對稱軸，并指出對稱軸與直線AB有怎樣的位置關系。

（2）設⊙O的半徑為r，圓心O到直線AB的距離為d，則d與r的大小關系分別是：

圖甲 ，圖乙 ，圖丙 。

學生認真閱讀課本“圓與圓的位置關系”的內容，回答下列問題：

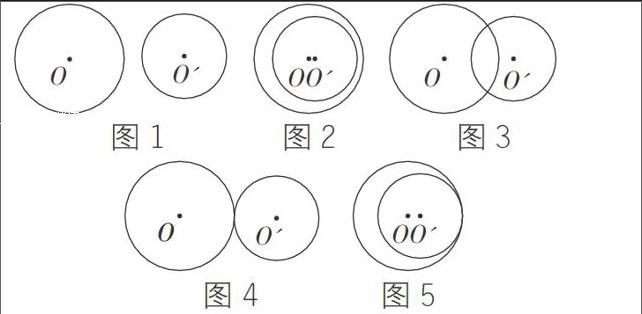
①如圖，同一平面內兩個不等圓之間的位置關系有以下5種，請分別寫出其名稱。

②圖1～圖5都是軸對稱圖形嗎？如是，請分別在圖中畫出它們的對稱軸.

自主學習是貫穿所有人一生的學習方式，也是人賴以生存、安身立命的基礎。自主學習源于模仿，而后不斷超越。就像運動員在正式比賽前要做熱身準備一樣，自主學習就是教師講解前的熱身，是學習的起始。自學能夠提高學生在校學習的質量，而學習不理想的主要原因是自學能力不強。

依據其年齡所應有的正常心智水平，中學生已經具備這樣的自學能力。自主學習對學生理解所學的知識很重要。正如要想聽懂交響樂，就必須了解作者的思想及樂曲所描述主題的時代背景，同時還可以根據自己的生活經歷、體驗去理解交響樂，這樣才能感受到它的意境、形象、情感，引起聯想，受到感染。

2.互助探究。互助探究不僅在課堂，如有必要，在課前、課后均可進行。

課前：完成對課本疑難點的互動探究。具體為核對課本習題的答案，解答組內成員對課本問題的疑難問題。若有困難，可尋求教師或學習小組其他成員的幫助。

課中：一是核對課前案和課中案中問題的解答，討論課中案中的疑難問題，若仍有困難，可在課中當場提出；二是共同分享各自的學習亮點。

課后：一是完成對教師批改后的課后案及測試卷中存在的問題的互動探究；二是對其他可能的問題互動探究。

在課中案中有這樣一個問題：如“課前案”圖1～圖5，設圓心距為d，⊙O的半徑為R，⊙O'的半徑為r，問：d與R和r分別具有怎樣的數量（大小）關系？（用等式或不等式分別表示出來）反之，能否用d與R和r之間的數量關系來判斷兩圓的位置關系？

此問題與“課前案”遙相呼應，通過互助探究，給完成“課前案”有困難的學生一個再認知的時間和機會，同時暗示“互逆現象”在數學命題間的廣泛存在，并學會用線段圖法探究此類問題。

互助探究就是讓全體學生積極主動地參與到學習活動中來。只有互動，才能互助。為此，我們要改變傳統課堂中的兩個唯一：講臺是課堂的唯一中心，教師是學生的唯一中心。

3.展示交流。展示交流就是把學生的自主學習和互助探究的成果公開化。在課中案中有這樣一個拓展問題設計：

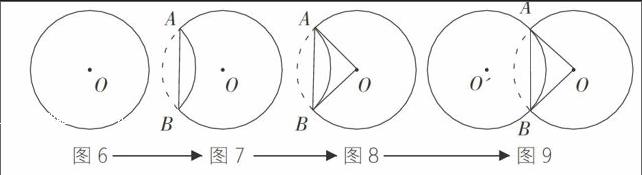
準備一張圓形紙片，將圓的一部分向內折疊，得折痕AB（AB即為圓的一條弦），連接OA，OB，得△OAB，如圖6～圖9。

1.△OAB是何種特殊三角形？

2.如圖10∽圖11，隨著折痕AB不斷變長，∠AOB的度數也在不斷地發生變化。已知⊙O的半徑為R，設∠AOB=α。

①當AB在什么范圍時，α為銳角？②當AB在什么范圍時，α為鈍角？③如圖11，當AB為何值時，α=60°？④如圖12，當AB為何值時，α=90°？⑤如圖13，當弧AB經過點O時，α值是多少？∠MAN的度數是多少？⑥猜想：弧AB的長與α之間存在怎樣的函數關系？

教師通過折圓的問題情境，將圓的一部分向內折疊，使研究對象從一個圓轉化為兩個圓（等圓），問題自然、清新、優雅，為學生展現探究問題的新角度，培養學生有效地認識問題本質的能力。通過展示交流，學生不僅再現了小學圓和弧的知識和初二函數的知識，又為下一節新課“弧長及扇形的面積”打下伏筆和基礎，同時讓學生感悟問題探究的方法，使學生逐步實現從掌握解題技巧到知曉思想方法的跨越，向“復雜的問題簡單化、簡單的問題深刻化”這一目標靠攏。

4.教師點撥。課堂的另一主體應該是教師，所以教師之于學生的學習是不可或缺的。如筆者提出了一個問題：“同一平面內兩個不等的圓之間的位置關系”這句話中有兩個限制條件，你能把它們找出來嗎？為什么要有這兩個限制條件？通過提問式的點撥，指導學生有效閱讀，探尋“等圓”的特殊位置關系，滲透“從特殊到一般”的思想方法。

從優秀走向優雅，不僅是課堂教學的追求，也是每一位教師的教育追求。做一位有思想的教師，在課堂上傳遞一種態度，也許能讓受眾與自身的心靈泛起些許漣漪，而這正是我們教師的價值所在。

黃金聲 “旋轉中的特殊到一般”教學設計片段

從特殊到一般（包括從一般到特殊）是人們認識世界的基本思想方法之一，這一思想方法在數學的認識活動中有著重要的應用。本課例試圖給出幾何問題的一種探究思路，在深度解讀問題背景中的一種基本數學思想——從特殊到一般的同時，強調課堂要從學生思維出發，促進學生思維能力發展，從而構建課堂教學新秩序。

【片段一】投石問路，激發動機

【問題1】將線段AB繞點A逆時針旋轉60°得到線段AC，繼續旋轉得到線段AD，連接CD，BD，如圖1。

（1）設∠BAC為α，若α=80°，則∠BDC的度數為__________；

（2）在第二次旋轉過程中，若角α的度數變化，請探究∠BDC的大小是否改變。若不變，請求出∠BDC的度數；若改變，請說明理由。

生1： 在第（1）問中 ∠BDC=30°，

在第（2）問中，∠BDC不變。

∠BDC=∠ADC-∠ADB==30°。

師：這是一種基于問題本質的解法，隨著學習的不斷深入，我們要不斷發展自己的數學思維，正如我們在做“3+3”時，不必總是從基本的“1+1”開始。同學們想一想，還有更好的解題思路嗎？

生2：以A為圓心，AB為半徑作圓，B，C，D在同一個圓上，這樣∠BDC與∠BAC就是同弧上的圓周角和圓心角。所以∠BDC=∠BAC=30°。

師：若將旋轉角一般化，即0°< α <360°，∠BDC的大小如何變化呢？

生3：若點D在優弧上，∠BDC=30°；若點D在劣弧上，∠BDC=150°。

師：真不錯！

……

【設計意圖】本教學設計片段通過教師有效點撥，實現兩次思維轉折：第一次是生2的解題思路即是思維生產（產生新思維）；第二次是生3基于數學思想的分類討論。通過兩次思維轉折，真正實現讓課堂從思維出發。

【片段二】經典點撥，拓展延伸

師：如圖2，△ABC為等邊三角形，點M為BC的中點，若△ABD和△ACE是全等的等腰直角三角形，把△ABD和△ACE繞點A任意旋轉，DM和ME有怎樣的數量關系和位置關系？

生：有垂直和相等的關系。

師：類似地，還可以提出什么問題？

師：一般地，我們還可以把圖2中全等的等腰直角三角形改為一般的全等直角三角形（∠ABD=∠ACE），DM和ME關系又如何呢？

生：（小組討論）DM和ME仍然相等，它們不垂直，但有

∠DME=∠DBA+∠ECA。

師：想想看，還可以怎樣把問題背景一般化？

生：（小組討論）若把一般的全等直角三角形改為如圖3所示的相似直角三角形（∠ABD=∠ACE），DM和ME的關系是否會發生改變呢？

生：DM和ME仍然相等，且∠DME=∠DBA+∠ECA。

師：很棒！圖形的背景條件改變了，旋轉后圖形的位置變了，問題的結論也發生了相應的變化，這就是變中之不變，不變中之變。

【設計意圖】在這個片段的教學過程中，全方位地展現了 “321實效課堂”教學改革的基本流程，即“自主學習、互助探究、展示交流、教師點撥”，讓展示交流使自主學習和互助探究的成果公開化，讓教師點撥成為學生思維升級的助推器，從而使課堂教學落到實處。（作者單位：江西省臨川第二中學）■

□責任編輯：周瑜芽

Email：jxjyzyy@163.com