非完整統(tǒng)計概率分布的冪律化

李亞亞 胡婭婭

摘 要： 根據(jù)非完整統(tǒng)計的思想，利用最大熵原理，在約束條件下，推導了非廣延參數(shù)相同和不同情況下正則系統(tǒng)和巨正則系統(tǒng)的統(tǒng)計分布，并借助Matlab繪制概率分布曲線。結(jié)果表明，當約束條件中非廣延參數(shù)相同時，其概率分布為指數(shù)形式，這與Tsallis統(tǒng)計分布的冪律形式顯然不一樣；當約束條件中非廣延參數(shù)不相同時，其概率分布不能精確求解，通過仿真擬合實現(xiàn)了冪律化。

關鍵詞： 非完整統(tǒng)計； 統(tǒng)計力學； 仿真； 冪律化

中圖分類號： O 414 文獻標志碼： A 文章編號： 1671-2153（2015）05-0094-03

1 提出問題

在復雜的物理系統(tǒng)中，如果不考慮系統(tǒng)內(nèi)粒子之間的相互作用，就能夠統(tǒng)計出可能出現(xiàn)的所有微觀態(tài)的數(shù)目w，即有pi=1。如果考慮系統(tǒng)內(nèi)粒子與粒子之間相互作用時，由于系統(tǒng)內(nèi)相互作用的復雜性等因素的影響，導致無法準確統(tǒng)計可能出現(xiàn)的微觀態(tài)的數(shù)目。設能夠統(tǒng)計的微觀態(tài)的數(shù)目為？淄，即有piq=1，把q稱為非廣延參數(shù)。其中？淄可能大于w，也可能小于w；當？淄=w時，所對應的統(tǒng)計為完整統(tǒng)計，當？淄≠w，所對應的統(tǒng)計為非完整統(tǒng)計，這是Q.A.Wang于2001年提出的非完整統(tǒng)計思想[1-2]，同時對統(tǒng)計力學中的shannon熵進行了變形，得出非完整shannon熵，即SqI=-kpiqlnpi，上標I代表非完整統(tǒng)計。在統(tǒng)計物理中，只要確定了所研究系統(tǒng)的概率分布函數(shù)，利用概率分布可得到統(tǒng)計系統(tǒng)的宏觀性質(zhì)。本文根據(jù)非完整統(tǒng)計思想，利用最大熵原理，推導了基于非完整shannon熵的正則分布（也稱為E分布）和巨正則分布（也稱N-E分布）。通過仿真，實現(xiàn)了統(tǒng)計分布的冪律化。

2 非完整shannon熵的E分布

若系統(tǒng)與源之間僅僅有熱交換，這里忽略系統(tǒng)的粒子數(shù)漲落和體積漲落而認為各微觀態(tài)的粒子數(shù)和體積取一定值N，V。由于熱源很大，系統(tǒng)在源的作用下，各微觀態(tài)的能量？著i可能不同，但在系統(tǒng)和源達到平衡時，系統(tǒng)的平均能量E是一定的，以Pi表示系統(tǒng)微觀態(tài)的概率，取約束條件：

piq=1， （1）

piq？著i=E。 （2）

根據(jù)非完整統(tǒng)計思想，式（1）和式（2）可能具有不同的q值，這里假定它們相同的條件下，根據(jù)最大熵原理，所求的統(tǒng)計分布應使非完整shannon熵

SqI=-kpiqln pi， （3）

在約束下取極值，就可得到正則系統(tǒng)的統(tǒng)計分布。

引入Lagrange函數(shù)：

L=-+？酌（piq-1）+β（piq？著i-E）， （4）

求條件極值，=0得：

pi=e=， （5）

Zq（β，N，V）=e？酌=[exp（-βq？著i）]1/q ， （6）

其中：β，？酌為Lagrange乘子。因子e-？酌相當于歸一化常數(shù)，當？酌=0，說明式（5）是歸一化的。將式（5）和（6）分別稱為E分布的概率分布函數(shù)和配分函數(shù)。

將式（5）帶入式（3），并應用式（1）和式（2），可將式（3）化為

SqI=k[βE+lnZq（β，N，V）]， （7）

依據(jù)熱力學基本關系：

N，V=kβ=， （8）

可得：

β=， （9）

則系統(tǒng)的平均熱力學公式為

E=-lnZq（β，N，V）， （10）

式中：T為絕對溫度；k玻爾茲曼常數(shù)。從式（9）中可以看出，β具有溫度的性質(zhì)，有時也稱之為統(tǒng)計溫度，很顯然，當q=1時，就回到完整統(tǒng)計。

3 不同非廣延參數(shù)下的E分布

由于系統(tǒng)內(nèi)粒子相互作用的復雜性，根據(jù)非廣延統(tǒng)計的思想，不論是約束條件，還是非完整shannon熵所對應的非廣延參數(shù)可能不相同，由此將式（1）～式（3）改為

pia=1， （11）

pib？著i=E， （12）

SqI=-kpiclnpi， （13）

根據(jù)最大熵原理，應使式（13）在式（11）和式（12）的約束下取最大值。

引入Lagrange函數(shù)：

L'=piclnpi+？酌（pia-1）+β（pib？著i-E）， （14）

求條件極值，=0得：

lnpi=， （15）

式中：a，b，c為不等于零的實數(shù)。式（15）是不同非廣延參數(shù)下E分布函數(shù)，由于a，b，c取值的變化性，要計算某一能量為？著i的微觀態(tài)所對應的概率Pi，是非常困難的，只能借助計算機仿真模擬。

4 不同非廣延參數(shù)下的N-E分布

如果系統(tǒng)與熱源之間僅有粒子和熱交換，且系統(tǒng)的各微觀態(tài)的體積具有同一個固定值V時，此時所對應的系統(tǒng)為巨正則系統(tǒng)（或稱N-E系統(tǒng)）。取系統(tǒng)限制條件：

piaNi=N， （16）

pib？著i=E， （17）

pic=1， （18）

Sq=-kpidln pi， （19）

引入Lagrange函數(shù)：

L=-+？酌（pic-1）+α（piaNi-N）+β（pib？著i-E），

（20）

式（20）中的α，β和γ為拉格朗日乘子。求？墜L/？墜pi，并令？墜L/？墜pi=0，得概率分布為

dpidlnpi+pid+αaNipia+βb？著ipib+？酌cpic=0。 （21）

式（21）也稱為不同非廣延參數(shù)下N-E分布，顯然其概率分布非常復雜，只能借助計算機仿真模擬。

5 仿真模擬

由于不同非廣延參數(shù)下E分布函數(shù)和不同非廣延參數(shù)下N-E分布表達式非常復雜，通過仿真模擬來反映各量之間的函數(shù)關系。

在式（15）中，令pi=y，β？著i=x，為了保證？著i=E為常量時，有pibEi=E，即保證能量守恒規(guī)律的滿足，令a=b，有

x=-？酌。 （22）

按照冪率形式利用Matlab軟件進行擬合，任意取a=b=0.96，c=0.98，？酌=-10，便可得到擬合曲線（圖略）。擬合方程為

y=-0.0039x5+0.2117x4-4.6422x3+51.2697x2-

285.6103x+643.2631，（23）

由式（23）可以看出，擬合方程實現(xiàn)了冪律化。

在式（21）中，令αNi=x，pi=y，β？著i=z，則

z=-yd-blny-yd-b-xya-b-？酌yc-b。 （24）

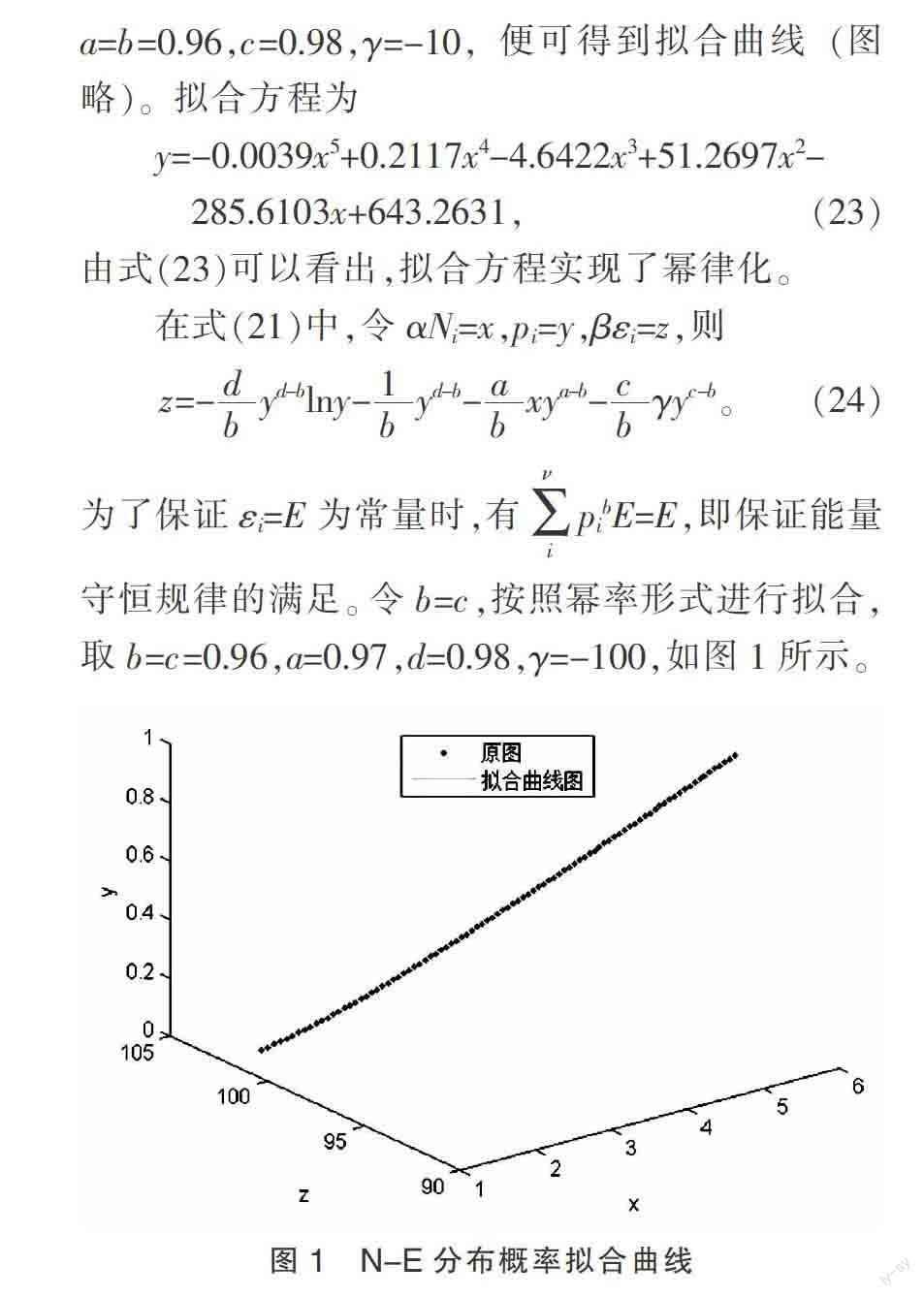
為了保證？著i=E為常量時，有pibE=E，即保證能量守恒規(guī)律的滿足。令b=c，按照冪率形式進行擬合，取b=c=0.96，a=0.97，d=0.98，？酌=-100，如圖1所示。

y=-0.6842+0.2032x0.9968+0.2233z0.2076， （25）

擬合之后，誤差的平方和為1.8121×10-7，很好的實現(xiàn)了巨正則分布的冪律化。

在正則系統(tǒng)和巨正則系統(tǒng)中，由等概率假設和各態(tài)歷經(jīng)假設所得到的統(tǒng)計分布函數(shù)是指數(shù)形式[3]，而1988年巴西物理學家Tsallis設計了非廣延的Tsallis熵，基于其推導出了Tsallis形式的冪律形式[4]。凝聚態(tài)物質(zhì)中的分形行為[5]，反常擴散等須用冪律分布來解釋；群集動物的社會行為和覓食行為也都表現(xiàn)出遵循冪律分布。在本文中，基于非完整shannon熵推導出非完整的正則分布（式（15））和巨正則分布（式（22））的函數(shù)形式非常復雜，通過計算機仿真模擬，實現(xiàn)了粒子之間相互作用復雜系統(tǒng)分布的冪律化，為研究一類遵循冪率分布的復雜系統(tǒng)提供了依據(jù)。但指數(shù)形式分布與冪律形式分布之間是否有聯(lián)系？如果有，究竟是什么因素導致它們之間的這種聯(lián)系，有待于深入探索。

參考文獻：

[1] QIUPING A W. Incomplete statistics and nonextensive generalizations of statistical mechanics[J]. Chaos， Solitons and Fractals，2001，12：1431-1437.

[2] 李亞亞，胡婭婭. 非完整統(tǒng)計在完全開放系統(tǒng)中的概率分布[J]. 大理學院學報，2013，12（4）：34.

[3] 李鶴齡，宋金國，雷潤潔. 非廣延統(tǒng)計力學與完全開放系統(tǒng)的統(tǒng)計分布[J]. 大學物理，2010，29（5）：17-22.

[4] TSALLIS C. Possible generalization of Boltzmann-Gibbs statistics[J]. J. Stat. Phys.，1988，52（1-2）：479-487.

[5] RAFAEL M. Fernandes and Jorg Schmalian[J]. Phys. Rev. Lett.，2011，106：67004.