淺析初中數學中全等三角形的教學設計

鄭維軍

老師常說，小學到初中，再到高中，傳統的教學方法已經湮滅年輕一代積極主動、善于思考的本性，以致于他們到了大學甚至出了社會工作都缺乏創新的能力，中國不缺乏勤奮苦干的人，缺少的是能開發、會創新的人才。要想徹底突破思想的禁錮，就必須從教學方法開始，老師應該以培養學生的主動思考意識為目的，探索新的教學方式方法。

初中數學是人們生活中不可缺少的一部分。它是開發思維的一門學科，也是學技術的基礎，同時也是智力的體現。它可以開發人的智力，培養人的思維能力，挖掘人的內在潛力，提高人們分析問題和解決問題的能力。所以，初中數學教學要求教師一定要引導學生思考，開發學生的思維能力，以培養學生的主動思考意識，如何來培養學生的主動思考意識呢？筆者在多年的初中數學教學中通過實踐總結出了一系列經驗和方法，最有效的手段是做好一份引導學生的教學設計并實施，本文我以全等三角形為例，如何設計引導學生學習從而達到預期教學目的。

全等三角形是初中幾何比較簡單的部分，掌握這部分內容是學習三角形相似及四邊形的基礎，是做一系列復雜證明題必須掌握的，也是整個幾何學習的開端。學好全等三角形能引導學生認真、饒有興趣地學習后面的內容。

（一）教學目標

1.知道什么是全等形、全等三角形及全等三角形的對應元素；

2.知道全等三角形的性質，能用符號正確地表示兩個三角形全等；

3.能熟練找出兩個全等三角形的對應角、對應邊。

（二）教學重點、難點

重點是全等三角形的性質；難點是找全等三角形的對應邊、對應角。

（三）教學過程

1.提出問題，創設情境，引導學生主動思考

⑴ 問題：你能發現這兩個三角形有什么美妙的關系嗎？

這兩個三角形是完全重合的。

⑵ 學生自己動手（同桌兩名同學配合）

取一張紙，將自己事先準備好的三角板按在紙上，畫下圖形，照圖形裁下來，紙樣與三角板形狀、大小完全一樣。

⑶ 獲取概念

通過前面的引導讓學生開動大腦用自己的語言敘述：全等形、全等三角形、對應頂點、對應角、對應邊，以及有關的數學符號。大概有三分之一的學生踴躍的舉手，等他們一個個說出自己的答案之后，我就告訴他們新婚卻的答案，這樣他們就比較深刻的記住了。

形狀與大小都完全相同的兩個圖形就是全等形。

要是把兩個圖形放在一起，能夠完全重合，就可以說明這兩個圖形的形狀、大小相同。

概括全等形的準確定義：能夠完全重合的兩個圖形叫做全等形。請同學們類推得出全等三角形的概念，并理解對應頂點、對應角、對應邊的含義.仔細閱讀課本中"全等"符號表示的要求.

2.導入新課

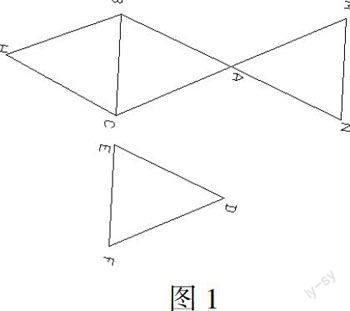
將△ABC沿直線BC平移得△DEF；將△ABC沿BC翻折180°得到△HBC；將△ABC旋轉180°得△AMN，如圖1所示。

議一議：各圖中的兩個三角形全等嗎? 通過一番激烈的討論，我們得出的結果是結果是：

△ABC≌△DEF，△ABC≌△HBC，△ABC≌△AMN.

（注意強調書寫時對應頂點字母寫在對應的位置上）

圖1

啟示：一個圖形經過平移、翻折、旋轉后，位置變化了，但形狀、大小都沒有改變，所以平移、翻折、旋轉前后的圖形全等，這也是我們通過運動的方法尋求全等的一種策略。

觀察與思考：尋找圖1中兩三角形的對應元素，它們的對應邊有什么關系？對應角呢？

引導學生從全等三角形可以完全重合出發找等量關系，從而得到全等三角形的性質：全等三角形的對應邊相等.全等三角形的對應角相等。接下來通過三個列子來加強記憶，達到舉一反三的目的。同樣是學生先思考，然后在黑板上把他們的過程寫出來，然后由我來講。

[例1]如圖，△OCA≌△OBD，C和B，A和D是對應頂點，說出這兩個三角形中相等的邊和角。問題：△OCA≌△OBD，說明這兩個三角形可以重合，思考通過怎樣變換可以使兩三角形重合?

將△OCA翻折可以使△OCA與△OBD重合。因為C和B、A和D是對應頂點，所以C和B重合，A和D重合。∠C=∠B；∠A=∠D；∠AOC=∠DOB。AC=DB；OA=OD；OC=OB。

總結：兩個全等的三角形經過一定的轉換可以重合.一般是平移、翻轉、旋轉的方法。

[例2]如圖，已知△ABE≌△ACD，∠ADE=∠AED，∠B=∠C，指出其他的對應邊和對應角。

分析：對應邊和對應角只能從兩個三角形中找，所以需將△ABE和△ACD從復雜的圖形中分離出來。

根據位置元素來找：有相等元素，它們就是對應元素，然后再依據已知的對應元素找出其余的對應元素。常用方法有：

（1）全等三角形對應角所對的邊是對應邊；兩個對應角所夾的邊也是對應邊。

（2）全等三角形對應邊所對的角是對應角；兩條對應邊所夾的角是對應角。

解：對應角為∠BAE和∠CAD；對應邊為AB與AC、AE與AD、BE與CD。

[例3]已知如圖△ABC≌△ADE，試找出對應邊、對應角。這個題就由學生討論完成。?? 借鑒例2的方法，可以發現∠A=∠A，在兩個三角形中∠A的對邊分別是BC和DE，所以BC和DE是一組對應邊。而AB與AE顯然不重合，所以AB與AD是一組對應邊，剩下的AC與AE自然是一組對應邊了。再根據對應邊所對的角是對應角可得∠B與∠D是對應角，∠ACB與∠AED是對應角。所以說對應邊為AB與AD、AC與AE、BC與DE.對應角為∠A與∠A、∠B與∠D、∠ACB與∠AED。

做法二：沿A與BC、DE交點O的連線將△ABC翻折

180°后，它正好和△ADE重合。這時就可找到對應邊為：AB與AD、AC與AE、BC與DE。對應角為∠A與∠A、∠B與∠D、∠ACB與∠AED。

3.課堂練習

課本練習1。經過上面的講解，同學們很輕松就完成了這個練習。

4.課時小結

這個環節是非常重要的，它是一個總結概括的行為。所以一定要讓同學們親自說出來，從學習委員開始，經過很多人的補充完善，大家七嘴八舌地就很全面地總結了本次課的內容。通過本節課學習，我們了解了全等的概念，發現了全等三角形的性質，并且利用性質可以找到兩個全等三角形的對應元素，這也是這節課大家要重點掌握的。找對應元素的常用方法有兩種：

第一、從運動角度看

1.翻轉法：找到中心線，沿中心線翻折后能相互重合，從而發現對應元素。

2.旋轉法：三角形繞某一點旋轉一定角度能與另一三角形重合，從而發現對應元素。

3.平移法：沿某一方向推移使兩三角形重合來找對應元素。

第二、根據位置元素來推理

1.全等三角形對應角所對的邊是對應邊；兩個對應角所夾的邊是對應邊。

2.全等三角形對應邊所對的角是對應角；兩條對應邊所夾的角是對應角。

綜上所述，無論在日常的生產和生活中，還是在涉及生存和發展的關鍵時刻，數學都起著非常重要的作用。通過教學方案的設計，創設問題情境，引導學生自主思考，使學生開動大腦跟隨老師的教學積極回答問題。從而使學生養成積極主動思考問題的習慣，為以后的學習和工作奠定思維基礎。培養學生積極主動地思意思不僅有利于個人的學習和工作，也是素質教育的要求，高全民族的數學素質，培養具有創新能力的人才，更是我們初中數學基礎教育應有的教學元素。