中學教學中滲透數學模型思想的初探

孫蘭香

摘 要：在日常生活中，隨時可以用數學知識解決生活中的實際問題的。“數學建模就是把一個具體的實際問題轉化為數學問題，然后我們用數學方法解決它，之后我們再把它放回到實際生活當中去，用我們的模型解決現實生活中的種種現象。”

1.在新課教學中注重數學建模

在傳統的教育觀念下，中學數學教學中學生學習方式主要以接受知識經驗為主，忽視自主嘗試、探索、建構知識結構，這將影響學生的終身數學發展。數學建模恰恰能改變這種弊端，數學建模注重在數學學習中建立某種數學模型，引導學生發現解決問題的辦法，讓學生自主探索數學內在的知識與實踐應用，利用動手實踐、自主探索、合作交流等學習方式開展數學學習活動。例如，“1.2活動思考”一課中，開展搭n個三角形與火柴棒根數的建模活動，教師設計六個層次的搭火柴棒動手實踐過程：①搭1個三角形需要火柴棒多少根？②搭2個三角形需要火柴棒多少根？③搭3個三角形需要火柴棒多少根？④搭10個三角形需要火柴棒多少根？⑤搭100個三角形需要火柴棒多少根？⑥搭n個三角形需要火柴棒多少根？學生動手實踐，自主探索，發現，第一個三角形需要三根火柴棒，以后每增加一個三角形需要增加兩根火柴棒，到搭n個三角形時，需要增加2（n-1）根火柴棒，即搭n個三角形需要火柴棒[3+2（n-1）]根，建構了數學模型，在建模活動過程中學生經歷了搭一搭、數一數、歸納等活動，建立了搭n個三角形與火柴棒根數之間的數學關系。在建構過程中，教師有意地引導學生積極思考和主動參與，動手實踐，改變以往被動地接受的學習方式，而是讓學生的大腦和雙手真正動起來。

2.在習題講解中滲透數學建模

數學模型是通過數學公式、程序、圖形、數學符號等對實際問題本質的描繪，它可以解釋某些客觀現象，也可以預測某些事物的發展規律，還可以為某一事物的發展提供最優的方案和解決方法。數學建模是聯系數學與日常生活實際問題的橋梁，可以使復雜的數學問題簡單化，在建立數學模型后，所有的問題、事物間的邏輯關系將一目了然，簡潔明了。在這些過程中都能促進學生進行“數學的思考”。例如，歲末年終，某甜品店讓利促銷，請運用本學期所學知識回答下列問題：①若香草口味蛋糕降價10%后的價格恰好比原價的一半多40元，該口味蛋糕原價是多少元？②若同一杯奶茶提供兩種優惠：一種是加量30%不加價，另一種是降價30%但是不加量。作為消費者，你認為哪種方式更實惠，為什么？

（1）設該蛋糕原價x元，根據題意得（1-10%）x=—x+40

解得x=100。答：該口味蛋糕原價100元。

（2）設這種奶茶原來售價a元每杯。①第一種方案，相當于每杯價格—=—≈0.77a元；②第二種方案，相當于每杯價格：（1-30%）a=0.7a元

因為0.77x>0.7x，故第二種方式實惠。

對于第①小問，學生只要能建立“降價后的價格=原價的一半+40”這樣的模型關系，就很容易解決。對于第②小問，在解決這類問題時，很多學生會無從下手，這就需要教師引導學生通過讀題、分析、歸納等思維活動，將本質屬性抽取出來，建構一個數學模型。在數學建模活動中，學生發揮想象力、創造力，靈活、合理地選擇解決問題的策略。他們獨立地思考，從數學建模的角度去探索和研究，并“數學地思考”，通過探索，構造出“現在每杯價格”的數學模型。通過建立數學模型解決該類問題，既可以清楚了解題中所給出的各個條件的作用，又可以將問題中復雜的邏輯關系簡單化。

3.在知識運用過程中注重數學建模

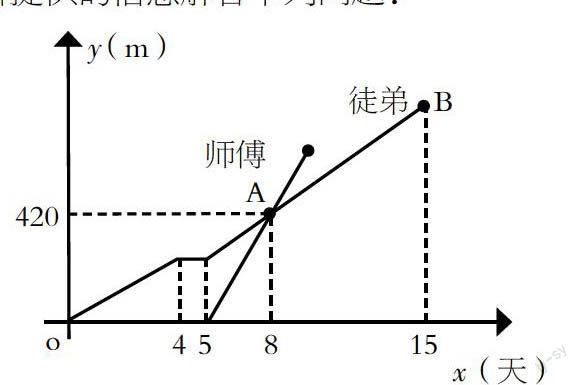
目前很多學生還沒有意識到“生活中處處存在著數學，處處存在著要用數學解決的問題”。因此，在我們學完某個知識點的內容之后，教師應利用學生生活中的事情作背景編制數學建模題。這樣，既運用了知識，又提高了學生數學的意識以及學習數學的興趣。例如在學習了函數這一知識點后，我編制了下面的習題：為了檢修自來水管道，由師徒兩人完成，兩人從管道兩端開始檢修，已知徒弟先修了4天后，休息了1天，接著師徒二人合做了5天，師傅被安排做其他的工作，余下的由徒弟單獨檢修完，下圖是師傅和徒弟修管道的長度與工作時間的函數圖象，請根據圖象所提供的信息解答下列問題：

（1）點A的實際意義：_________。

（2）求直線AB的函數關系式。

（3）這個自來水管道共有多少？

數學建模讓數學知識變無形為有形，從而形成一種更為被學生容易理解的數學結構。我們在教學中有意識地滲透數學建模思想，對培養學生思維品質的靈活性、創造性是十分有益的！

參考文獻：

[1]張思明.張思明與數學課題學習[M].北京：北京師范大學出版社，2006.

[2]姜啟源，謝金星，葉 俊.數學模型[M].北京：高等教育出版社，2003.

（作者單位：江蘇省南京市紫東實驗學校）