隨機條件下部門資本預算獨立方案的選擇
耿春燕
摘要:在項目現金流量是確定的條件下,求解部門資本預算獨立方案的選擇方法有:0~1整數規劃法、組合互斥化法和凈現值率排序法,但在構成方案現金流量的數據具有不確定或隨機性,即各期現金流量是隨機變量時,如何選擇部門資金預算的獨立方案。文章討論了在隨機條件下如何運用期望值準則及其可能性,并給出了數值案例演示了利用軟件在隨機條件下三種選擇方法一般求解過程。
關鍵詞:隨機變量;凈現值;期望值;最優組合方案
一、引言
部門資本預算,不僅涉及多個投資項目,而且涉及資金的數量,即在資金有限條件下投資項目如何優選的問題。在資金有限的條件下,如何選擇最合理、最有利的投資方向和投資項目,使有限的資金獲得更大的經濟效益,這就是企業進行資本預算時所面臨的資金分配問題。
在確定條件下,有資金約束條件下的獨立方案選擇,其根本原則在于使用有限的資金獲得最大的經濟效益,即組合方案的凈現值之和最大,實質上是個0~1整數規劃問題,其目標函數可以寫作: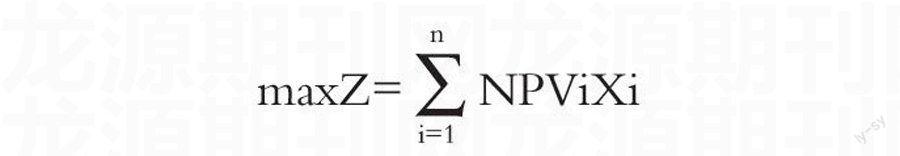
maxZ=NPViXi
式中NPVi——第 i個投資項目的凈現值;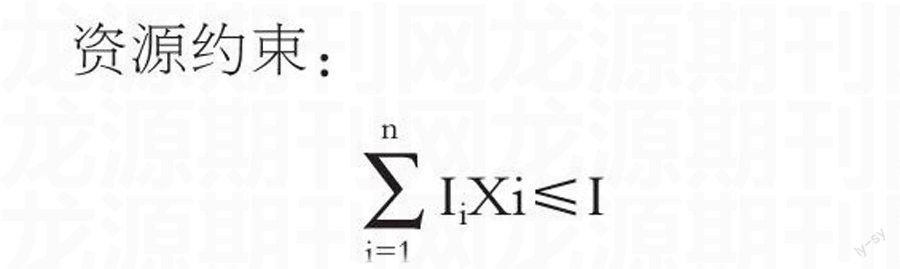
Xi——決策變量。其取值為1或 0。Xi取值為 1,表示第i個投資項目被接受;Xi取值為 0,表示第 i個投資項目被舍棄。i= 1, 2,…,n 。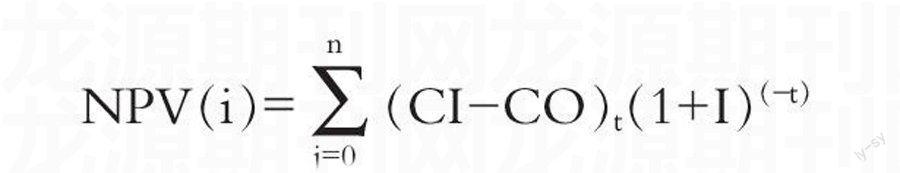
資源約束: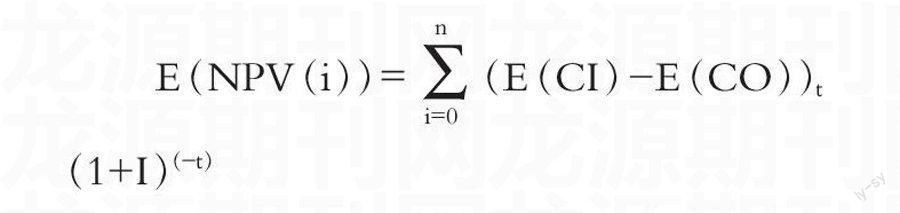
IiXi≤I
整數規劃法適用于當方案數(n)較多時,利用整數規劃的常用軟件(如LINDO或WinQSB)或EXCEL中自帶的規劃工具就可以快捷和方便地求解,且能在各種情況下均能保證獲得最佳的組合方案。
互斥組合法就是在資金限量條件下,選擇一組不突破資金限額而經濟效益又最大的互斥組合投資項目作為分配資金的對象。當存在多個投資項目時,不論其相互關系如何,都可以把它們組成許多互斥組合,并按凈現值、年值等指標計算各互斥組合的經濟效益,在不突破資金限額的條件下,選取經濟效益最大的一組投資項目作為分配資金的對象。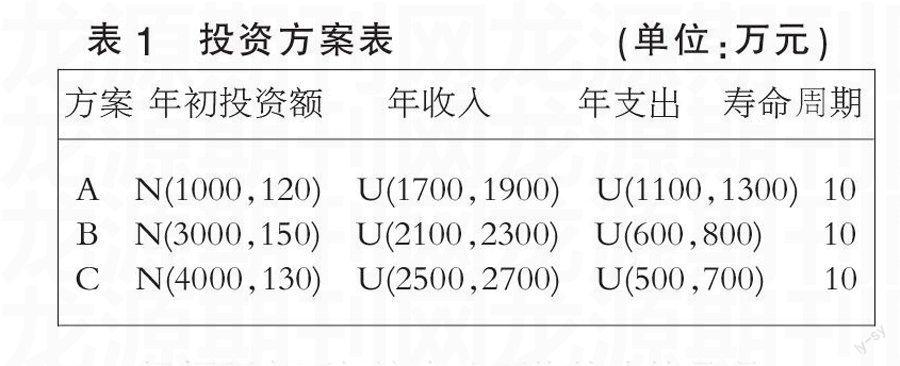
其評價的基本步驟如下。
第一,分別對各獨立方案進行絕對效果檢驗。即剔除NPV<0的方案。
第二,對通過絕對效果檢驗的方案,列出不超過總投資限額的所有組合投資方案,則這些組合方案之間具有互斥的關系。
第三,將各組合方案按初始投資額大小順序排序,按互斥方案的比選原則,選擇最優的方案組合,即分別計算各組合方案的凈現值,以凈現值最大的組合方案為最佳方案組合。
在有資金預算的條件下運用組合方案互斥法進行比選,其優點在于能保證獲得最佳的組合方案,但當方案數目較大時,于方案組合數(2n)較大,用組合互斥法雖然可行但是工作量較大,所以計算起來很繁瑣且容易錯誤。
凈現值率法是一種在計劃期資金限額內先選擇凈現值率大的投資項目,直到資金限額分完為止的項目選擇方法。其具體做法是把能滿足最低期望盈利率的投資項目,按凈現值率由大至小順序排列,首先將資金分配給凈現值率最大的項目,直到全部資金分完為止。
凈現值率法的優點在于應用簡單,一般能求得投資經濟效率較大的項目組合,但不一定能取得最優的項目組合。
以上的評價方法都是針對在確定條件下(各期現金流量為常數)的經濟評價。和確定條件下的經濟評價一樣,隨機條件下的經濟評價也主要面臨如何運用三種方法的進行評價問題。本文將探討隨機條件下,在期望決策準則下用上述方法選擇有資金預算的獨立方案。
二、隨機條件下的期望值準則及期望值
這里假設各方案的折現率為確定常數,在確定情況下方案凈現值的計算表達式為:
NPV(i)=(CI-CO)t(1+I)(-t)
CI 表示現金流入,CO表示現金流出,I表示折現率。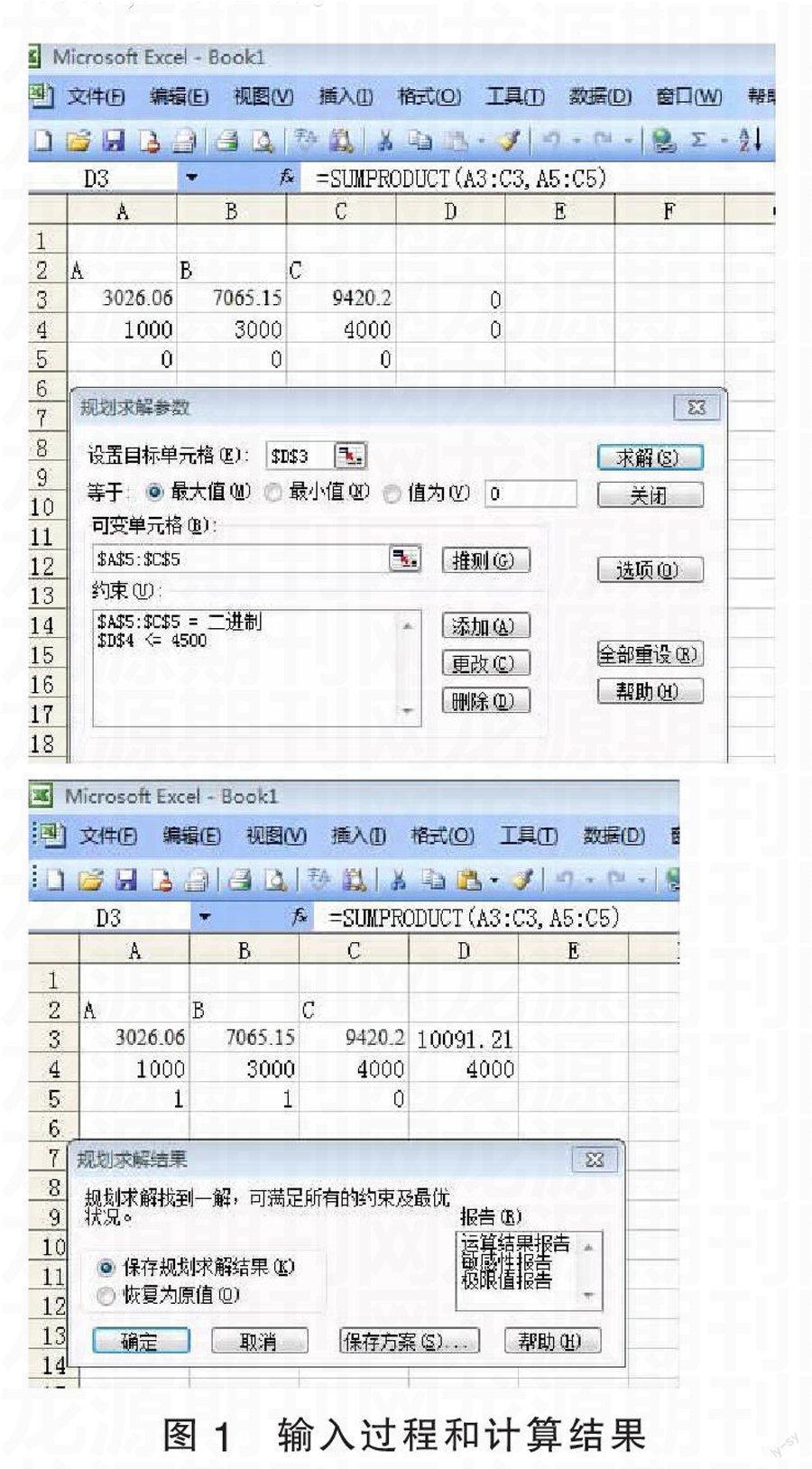
在隨機條件下各方案的現金流量是隨機變量,即CI 、CO是隨機變量,根據期望值準則取其期望值,就可以計算出每期確定的凈現金流量。進而可以得到各方案的凈現值期望值,便成為了確定條件下的情況了,就可以用三種方法來進行求解了。于是計算表達式就變為:
E(NPV(i))=(E(CI)-E(CO))t(1+I)(-t)
CI -現金流入,CO-表示現金流出,I-折現率
問題在于如何獲得期望值。關于這些值的一般計算方法在概率論和數理統計類教材和文獻中均有詳細介紹,在方案經濟評價中,確定期望值的主要途徑有兩種:一是利用中心極限定理確定。根據中心極限定理,當方案的現金流量足夠多時,方案的評價指標近似服從正態分布。因此,在此理論下,由于評價指標的分布已知,問題的關鍵在于確定出分布的期望值和方差值,當期望值和方差值已知,就可以利用正態分布標準化等技術計算概率值。二是利用隨機模擬確定。對于隨機條件下的問題基本上都可以采用隨機模擬求解期望、方差和發生概率。
三、案例計算
設某企業未來資金額是一隨機變量,且服從正態分布,N(4500,100)。現有A、B、C三個獨立方案,壽命期均為10年,且三個方案均滿足各方案的初始投資、年收益和年支出也均為隨機變量,具體如表1所示。公司要求的最低收益率為8%,該企業會選擇哪些方案?
根據題意可知該企業面臨的決策是現金流不確定條件下的有資金預算的獨立方案選擇問題。現金流量為一隨機變量,分布為正態或均勻分布,即年收入(CI) 、年支出(CO)是隨機變量,根據期望值準則取其期望值,就可以計算出每期確定的凈現金流量。進而可以得到各方案的凈現值期望值,便成為了確定條件下的情況了,就可以用三種方法來進行求解了。
確定各方案的凈現值期望值:
E(NPVA)=-1000+(1700+1900)/2 (P/A,8%,10)-(1100+1300)/2 (P/A,8%,10)=3026.06
E(NPVB)=-3000+(2100+2300)/2 (P/A,8%,10)-(600+800)/2 (P/A,8%,10)=7065.15
E(NPVC)=-4000+(2500+2700)/2 (P/A,8%,10)-(500+700)/2 (P/A,8%,10)=9420.2
上式中(P/A,8%,10)是年金現值系數,查表可知為6.7101。可知三個方案的凈現值期望值均大于零,三個方案都通過了“絕對效果檢驗”。
各方案投資期望值依次為:E(IA)=1000,E(IB)=3000,E(IC)=4000
1. 0~1整數規劃求解(利用EXCEL軟件)
在不確定情況下整數規劃的目標函數應該改寫為:
maxZ=E(NPVi)xi
式中NPVi——第 i個投資項目的凈現值;
Xi——決策變量。其取值為1或 0。Xi取值為 1,表示第i個投資項目被接受;Xi取值為 0,表示第 i個投資項目被舍棄。i= 1, 2,…,n。
資源約束:
E(Ii)xi≤E(I)
根據以上計算結果和函數,獲得該問題的0-1整數規劃模型
MAX(3026.06x1+7065.15x2+9420.20x3)
s.t 1000x1+3000x2+4000x3≤4500
x1,x2 ,x3=0或1
根據以上模型,利用EXCEL自帶的整數規劃工具或LINDO軟件可獲得結果,這里為方便使用了EXCEL中工具欄的整數規劃求解,選擇A和B,最大期望凈現值為10091.21,輸入過程和計算結果如圖1所示。
2. 互斥組合法
3個獨立方案可以有23 個互斥組合方案,如表2所。
從以表2中可知AC BC ABC 期望投資總額均超過期望的資本預算,舍去,故最優的方案組合為AB ,期望的最大凈現值為10091.21,與0-1整數規劃化解出結果的一致。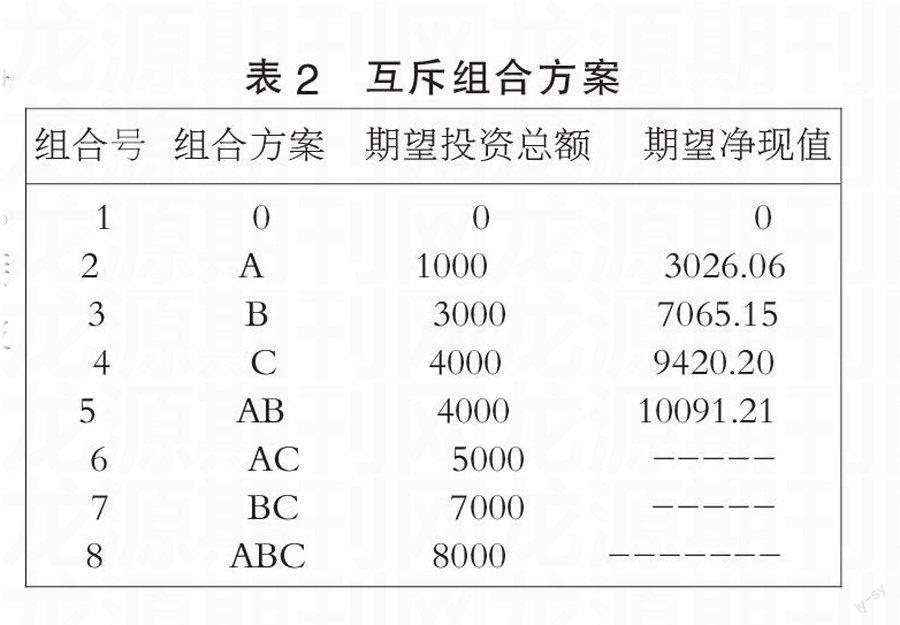
3. 凈現值率法
從表3可知,最佳方案組合投資為:A+B=4000(萬元)。最佳方案組合凈現值為:A+B=10091.21。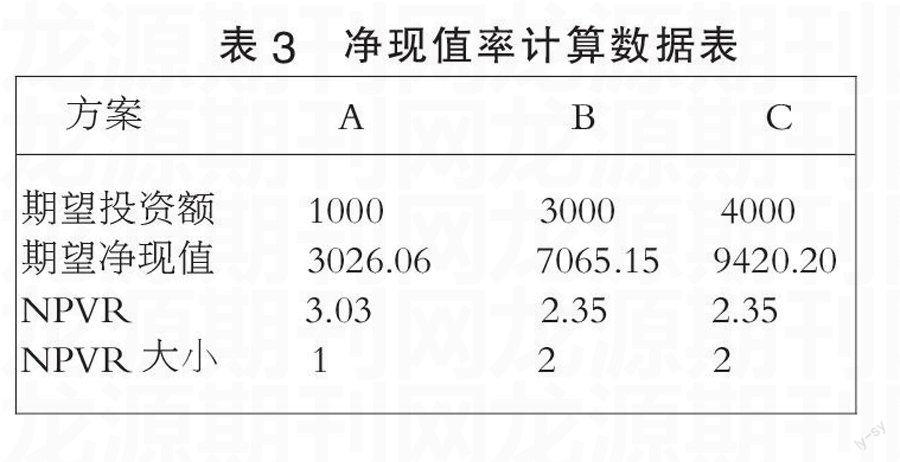
與前面二種方法結論一致。值得注意的是凈現值率法應用簡單,一般能求得投資經濟效率較大的項目組合,但不一定能取得最優的項目組合。在有明顯的資金總額量限制,且各項目資金遠小于資金總擁有量時,適宜用凈現值率進行方案選優。
四、結論
本文討論了在企業有資本預算,項目的現金流量是隨機變量條件下,用三種選擇方法0~1整數規劃法、組合互斥化法和凈現值率排序法的求解問題。利用中心極限定理或隨機模擬方法確定了方案的各期現金流量的分布和期望值,進而可以計算出各方案的凈現值期望值和投資期望值后。這些問題成為了確定條件下的情況了,就可以用三種方法來進行求解了。給出了實例,利用軟件求解了三種方法的一般過程,但本文未涉及如何利用中心極限定理或隨機模擬方法確定了方案的各期現金流量的分布和期望值,這是個需要認真研究的問題。
參考文獻:
[1]劉曉君,等.工程經濟學[M].北京:中國建筑工業出版社,2006.
[2]向壽生.Excel在投資項目概率分析中的應用[J].商業研究,2008(07).
[3]李國平.劉成,基于0-1規劃的EXCEL整數規劃求解[J].科教文匯,2009(06).
[4]邵穎紅.工程經濟學[M].上海:同濟大學出版社,2009.
(作者單位:重慶建筑工程職業學院)

