以“等邊三角形”為載體的“全等三角形復習”教學設計

●鄭愛素 (石浦中學 浙江象山 315731) ●奚喜兵 (丹城中學 浙江象山 315700)

以“等邊三角形”為載體的“全等三角形復習”教學設計

●鄭愛素 (石浦中學 浙江象山 315731) ●奚喜兵 (丹城中學 浙江象山 315700)

“用科學的理念指導數學復習教學，提升復習的有效性”是每一位數學教師所思考的問題.一節高效的復習課不但要回顧并應用所學的知識，還應該是知識的提高與升華，更是方法的提煉與總結，以及數學思想方法、思維能力的培養與訓練.在復習課的教學中應以教材典型問題為主線，適當變式、拓展，使其源于教材，又不拘泥于教材.筆者就浙教版《數學》8年級上冊中“全等三角形”這一章的復習課進行教學設計，將自己的一些想法與同行分享.

2 教學過程設計

2.1 開門見山，呈現例題，指明課題

教師陳述:“全等三角形”是解決有關線段相等、角相等的重要工具與手段;等邊三角形是一類特殊的三角形，在解題與考試中有較多的應用.本節課以“等邊三角形”為載體進行“全等三角形”的復習:

例1 如圖1，△ABC為等邊三角形，D，E是BC邊上的2個點，滿足BD=CE.

1)等邊三角形有哪些特性?

2)你能找出其中的一對全等三角形嗎?如何證明?

3)圖1中還有其他全等三角形嗎?如何證明?

4)圖1中有等腰三角形嗎?如何證明?

設計意圖 教師避開常規復習課對基礎知識的簡單羅列，開門見山呈現問題，一開始就調動學生的積極思維.例1以學生熟悉的等邊三角形為背景，設置了4個小問題.這4個小問題聯系緊密，從學生熟悉的等邊三角形出發，然后辨認全等三角形，再證明全等三角形，最后用全等三角形的性質說明等腰三角形，符合學生的認知規律.在教學時，教師可以先讓學生思考片刻，并在學案上完成任務，然后讓學生回答，并作出合理評價，鼓勵用不同的方法證明，培養一題多解的能力.

2.2 一題多變，優化學生的思維能力

一題多變體現了數學知識的層次性和數學知識點的多元性，從而能優化學生的思維，擴大學生的知識面，使學生對本題有更全面的認識和理解.

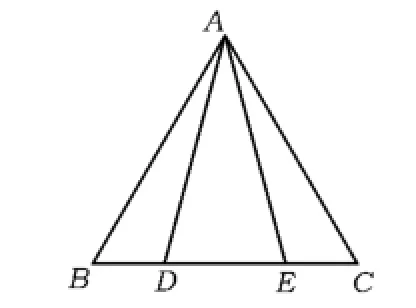
圖1

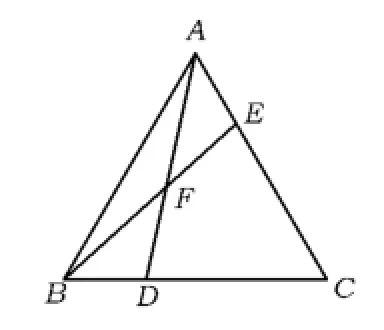
圖2

變式1 如圖2，△ABC為等邊三角形，點D，E分別在邊BC，AC上，滿足BD=AE，AD與BE交于點F.

1)圖2中有幾對全等三角形?分別寫出來并說明你判斷的理由.

2)圖2中有等腰三角形嗎?如何證明?

教學預設 對△ABD≌△BAE的證明，方法比較單一(SAS)，但判斷△BFD≌△AFE的方法比較多，學生可以相互補充;對第2)小題等腰三角形的辨認，學生根據圖形的直觀感覺，估計只能說出△ABF是等腰三角形，對圖形移動過程中產生的特殊情景很難作出判斷(△AEF和△BDF也是等腰三角形)，教師可以通過引導、啟發、追問等方式進行.

3)當點D，E的位置發生變化時，△BFD和△AFE有可能是等腰三角形嗎?

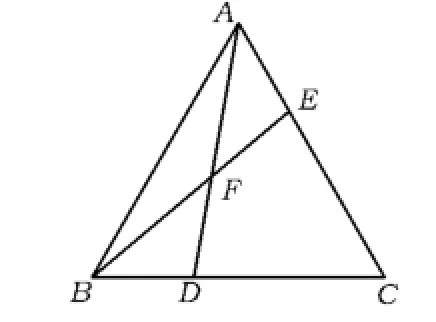
圖3

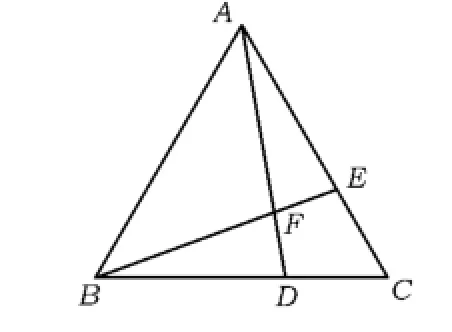
圖4

4)觀察:當圖3和圖4中的△BFD和△AFE是等腰三角形時，你能計算∠FBD的度數嗎?

(答案:圖3中∠FBD=40°，圖4中∠FBD= 20°.)

設計意圖 教師通過幾何畫板在圖2的基礎上，移動點D的位置(此時點E的位置相應地改變)，學生經過觀察幾何畫板設置的“度量結果線段的長度顯示”，發現圖3中DB=DF，EA=EF，而圖4中出現BD=BF，AE=AF，第3)小題得以解決;第4)小題中∠FBD度數的計算，需要用到三角形的內角和、外角性質等，還需通過解方程才能完成.

變式2 如圖5，△ABC為等邊三角形，點D，E分別在邊BC，AC上，滿足BD=CE. 1)圖5中△ABD≌△BCE成立嗎?如何證明? 2)還有其他全等的三角形嗎?如何證明?

3)在點D，E移動變化的過程中，∠AFE的大小是否發生相應的變化?如果有變化，請說出變化規律;如果沒有變化，請求出∠AFE的大小，并說明理由.

設計意圖 對于第1)小題，學生會用SAS的方法證明△ABD≌△BCE;對于第2)小題學生經過觀察、思考，應該能找出△ADC≌△BEA，并加以證明;第3)小題比較抽象，教師可以通過幾何畫板演示，點擊點D的位置并拖動，示意學生注意觀察∠AFE的度數是否變化，在學生直觀感知∠AFE的大小固定不變后，教師引導學生利用三角形的內角和、外角性質等加以計算，得出∠AFE的大小是60°.基本過程如下:

由△ABD≌△BCE得∠BAD=∠CBE，于是∠AFE=∠ABF+∠BAF=∠ABF+∠CBE=∠ABC=60°.

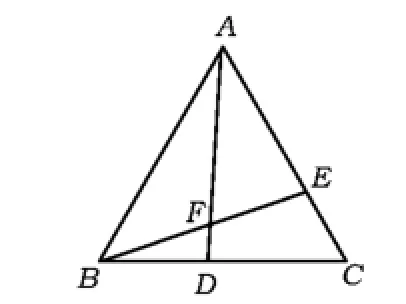
圖5

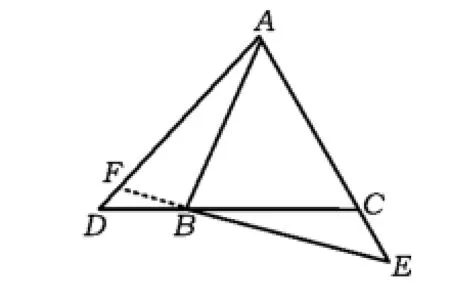
圖6

變式3 如圖6，若點D，E分別在邊CB，AC的延長線上，其他條件不變，變式2中的結論還都成立嗎?

(說明:課堂教學過程中，教師利用幾何畫板展示圖6中點D的移動過程，示意學生注意觀察相應角度的變化.)

設計意圖 通過一組變式題的交流研究，充分激發學生的求知欲，滿足不同層次學生的不同需求，提高課堂復習效率.通過不斷改變題中的條件，或者改變圖形的方式，促進解題思路的改變與解題方法的調整，有利于學生舉一反三，加深對數學核心知識的掌握，培養他們的自主學習能力和探究創新的科學精神.

2.3 多題一解，培養化歸思維能力

有不少數學習題雖然講述的不是同一件事，或者呈現方式不同，但是，它們的數學本質完全一樣，或是解題方法基本類似.將這樣一些表面各不相同而本質完全一樣的若干習題放在一起進行教學，可以培養學生的化歸思維能力.

例2 如圖7，△ABC，△EDC均為等邊三角形，點D，B，C在一條直線上，聯結AD，BE，延長EB交AD于點F.

1)找出圖7中的全等三角形，并說明理由;

2)求∠DFE的度數.

設計意圖 學生有了上面例1的解答與相關變式練習的解題經驗后，不難找出△ACD≌△BCE，但是∠DFE的度數計算就沒有∠AFE= 60°那么容易了，需要先求

∠AFB=∠ADE+∠DEF=

∠ADC+60°+∠DEF=

60°+∠DEF+∠CEF=

60°+60°=120°，

從而 ∠DFE=60°.

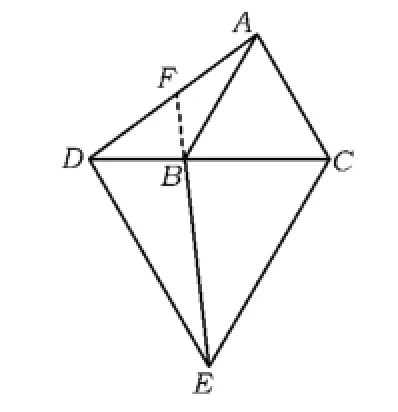
圖7

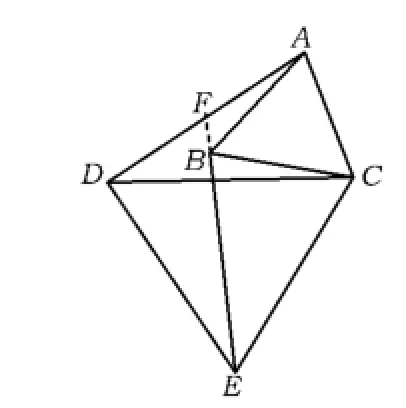
圖8

變式1 如圖8，當點D，B，C不在一條直線上時，此時例2中的結論還成立嗎?說明理由.

變式2 如圖9，點A，C，E在一條直線上，在同側作等邊△ABC和△EDC，聯結AD，BE，相交于點F.

1)圖中有幾對全等三角形，并說明理由;

2)求∠DFE的度數;

3)判斷CM與CN的大小關系，并說明理由.

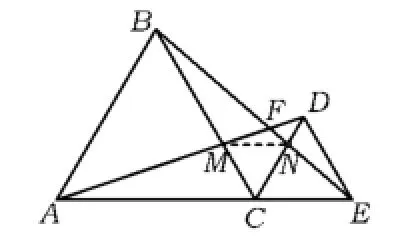
圖9

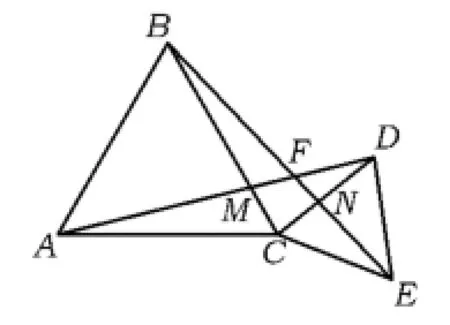
圖10

變式3 如圖10，當點A，C，E不在一條直線上時，上述結論還成立嗎?

設計意圖 3道變式題的解題思路基本相同，推理過程基本類似，學生在獨立思考基礎上通過同學之間交流，一般都能完成解答.解題過程只需學生個別口述，教師適當點評.通過例2與一組變式類比，可以培養學生的化歸思維，能夠透過現象看本質，多題歸一，以不變應萬變，提煉出數學規律，培養學生的類比能力.看似圖形位置發生了變化，其實解題思路、方法卻是相通的，只是變式2和變式3中求∠DFE的度數時，需要2次用到“三角形的外角性質”，說明CM=CN需要用到2次全等，從而進一步要求學生把握數學的本質，提升數學思維能力.

3 反思

3.1 復習課貴在主題明確，學生積極參與

提高數學復習課的效率，關鍵在于確定復習的主題，將教學的起點基于學生的認知起點和能力起點，設計相應的教學內容和教學活動，使各個層次的學生都能獲得相應的發展.本課設計以學生熟悉的“等邊三角形”為載體，以“全等三角形的判定與性質”為主題，通過變式(改變條件或改變圖形)教學，以“一題多變”、“多題一解”的形式，培養學生的數學思維能力.整節課的教學設計旨在使學生都能積極參與數學活動中.

3.2 復習課貴在學生有更多“說”的機會

新課程倡導學生的數學活動應當是一個生動活潑的、主動的和富有個性的過程.在這一過程中，學生是學習的主體，教師應有效發揮主導作用.本課設計中，圍繞一系列問題，在學生獨立思考的基礎上，教師始終把“說”的權力下放給學生:所發現的全等三角形、判斷的方法、解題的思路、觀察到的或猜測的等腰三角形、指定角的度數等等，都是讓學生先“說”，教師適當補充、提示、追問.在整個教學過程中，更多的是學生生動活潑地自主思考、探索和展示，學生能自己解決的、能表達的、能展示的內容，教師把“說”的機會充分地還給學生.

3.3 復習課貴在合理使用多媒體輔助與簡明學案并用

教師在課堂中合理使用多媒體輔助教學，利用幾何畫板演示，直觀展示了幾何圖形的變化過程，讓學生直觀上清晰感悟幾何圖形的特征，發現幾何規律，為猜想幾何結論提供了方向，為幾何命題的證明提供了方便.例1變式1中△AEF和△BDF都是等腰三角形，幾何畫板就提供了2個非常直觀的位置，只憑紙上固定的圖形，學生恐怕難以想到這樣的2種情形;例2及變式題的圖形通過幾何畫板，直觀展示了幾何圖形之間變化的無窮魅力.簡明學案的使用，讓學生動手動腦，一定程度上提高了學習效率，同時，對速度較慢的學生而言，可在課后繼續完成.