抑制光伏功率對電網影響的電池管理研究

趙向陽，王杏玄

(北京航空航天大學自動化科學與電氣工程學院，北京100191)

抑制光伏功率對電網影響的電池管理研究

趙向陽，王杏玄

(北京航空航天大學自動化科學與電氣工程學院，北京100191)

光伏功率難以有效預測、調度和控制，通過儲能系統直接與光伏并聯運行，可平抑光伏功率的隨機性，將其并網時對配電網電能質量的影響降到最低。主要研究使光伏發電的并網功率波動最小的電池管理方法，針對隨機量的一般波動性與多尺度波動性指標，提出了對光伏功率進行完全補償時基于定尺度窗口和變尺度窗口的電池充放電策略，通過仿真，將優化效果以及所需儲能系統的容量分別進行比較，得出變尺度窗口比定尺度窗口調度電池具有更好的平抑作用。

光伏并網；電池管理；定/變時間尺度

0 引言

光伏發電的波動性、隨機性在并網時給配電網的有功平衡和電壓調整帶來壓力，增加了配電網規劃和調度的難度。并網的成功與否在很大程度上取決于其輸出功率波動性的大小[1]。文獻[2]指出光伏功率具有明顯的波動性，在短時間內波動量可超過裝機容量的50%。為保證光伏安全并網，需要通過調節儲能電池對其輸出功率加以限制。文獻[1]總結出用不同概率密度函數擬合不同尺度下的光伏功率的出力。文獻[3,4]提出了完全補償的概念并針對儲能電池容量已知時電池以恒功率、功率差充放電對微電網與配電網聯絡線功率的平抑效果進行深入探討，但是沒有對完全補償時需要的電池容量進行詳細闡述。文獻[5]在考慮預測誤差的影響下研究了如何配置分布式光伏儲能系統容量。文獻[6]采用動態規劃法的電池儲能系統的削峰填谷作用進行優化，并在不同充放電次數下的效果進行對比。此外，許多外學者在研究平抑功率波動性方面已取得一定成果[7～17]，其中文獻[16]是用電動汽車換電站多個電池的有序充電來協同優化波動性功率，但是針對衡量光伏功率波動性的表述過于單一。

本文在討論隨機量均值、方差的基礎上，提出了定、變尺度窗口的概念，以平抑光伏并網功率的波動為目標，創新性的以一般、多尺度方差為評價指標，并對按定、變尺度窗口調度值完全補償功率波動所需電池容量和的優化效果進行比較。

1 電池的管理目標

在光伏并網的工程設計中，必須考慮儲能系統對并網功率的平抑效果，本文試圖通過控制儲能系統的充、放電使光伏并網功率的波動性最小，這里用以下兩種指標來衡量其波動性。

1.1 一般波動性

(1)峰谷差

文獻[12]從曲線的最大值、最小值入手抑制其波動性的2個函數為：

T時間內隨機量X最小值最大為：

f=max{min(X)}

(1)

充電時段內總曲線最大值最小為：

f=min{max(X)}

(2)

文獻[13]中以減小曲線峰谷差為目標函數：

FL=min[max(X)-min(X)]

(3)

(2)方差

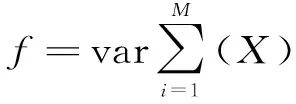
(4)

1.2 多尺度波動性

為了更全面地描述光伏功率的分布特點，應該研究其在不同時間尺度時的波動性。

(1)階躍變化率

將原序列的相鄰或相間隔數據相減后得到的新序列為原序列的階躍變化，再除以相減數據的間隔即為原序列的階躍變化率。階躍變化的絕對值可在一定程度上反映原序列的波動性大小[10,11]。

假設某序列P的采樣時間為Ts，期望在時間間隔為Td時衡量該間隔的階躍變化，定義階躍變化為：

(5)

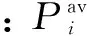
(6)

在此基礎上，考慮期望時間間隔的影響，可得到階躍變化率表達式：

(7)

這個期望時間間隔Td不同，其對應的階躍變化也不同，從而導致了光伏出力波動的多尺度特性。即假如采樣時間Ts為1min，分析每10min、30min、60min等時間間隔的平均功率時，期望時間間隔Td則依次為10min、30min、60min；N依次為10、30、60；若對應一天24 h的功率，L依次為144、48、24。

(2)M-界定

基于階躍變化、階躍變化率在衡量波動性時由于將波動平均化而導致計算的波動性偏低失真問題，“M界定”法應運而生，即將原序列在所給時間間隔內的最大值、最小值相減作為波動性的量化指標[8～10]。具體為：

M=Mup-Mlow

(8)

式中：Mlow≤x(t)≤Mup，?t∈[ε,ε+Δ]，ε為某一時間間隔的開始時刻。

(3)統計方差

文獻[14]將某隨機量劃分為若干窗口，其中第i個時間窗口內隨機量的平均值為：

(9)

則第i個時間窗口的隨機量的方差D為：

(10)

式中：sum(D) 為隨機量P的統計方差[5]；M為時間窗口的時段數；Pt為第t時段的隨機量；Pav,i為第i個時間窗口的隨機量平均值。選取不同的M值，可得到隨機量P的多尺度波動性，即不同尺度的衡量原來數據的波動性。M的合理取值為3～24，M越大對應的方差表示與該調度點越多的相鄰點的波動性；越小越能反映局部波動性。特殊地，當窗口尺度M為24時，sum(D)/(L-1)即為一般意義的方差。

2 電池管理策略

假設精細化調度時，采樣頻率為5 min，則在1 h內的光伏功率數據有12個，調度時間間隔15 min(窗口尺度至少為3個，變尺度時的要求)，本文提出的兩種調度思路。

2.1 策略1 定尺度調度

電池充放電的各個區間尺度相等，按n個小時的均值作為一個調度值，這里n滿足電池充放電次數和調度時間間隔的約束，可取范圍n=1/4～24 h；設充放電區間尺度為調度段的M倍，則待求一天的窗口總數為N=floor(24/M)+1，第i個階段的始、末節點為：

相鄰窗口時間搭界的始末節點為：

a(i)=(i-1)×(M-1)+1

(11)

b(i)=i×(M-1)+1

(12)

2.2 策略2 變尺度調度

此時，電池充放電區間尺度不等，但與策略1中區間個數一樣，而且每個窗口內的數據要不小于3個，調度值取為不同時間尺度的窗口均值。該思路由統計方差的思想啟發，將隨機量按波動程度劃分窗口。

各個窗口尺度的選取準則：當前調度節點至末尾調度節點，所有尺度下對應調度后標準差最小的尺度為最優時間尺度。設第k個節點對應第i個窗口(其中k≥i-1)，即前i-1個窗口對應的尺度已知，則第i個窗口對應的尺度為：

M(i)=min(std(pi))

(13)

其中，pi=[k,k+1…end]，end∈{k+1,k+2,…n}，pi為從當前節點k向后至末尾節點n所有尺度下的隨機量序列；波動最小的序列，即當前尺度M(i)∈{1,2,…24-k}。

第i個窗口的時間節點為：

a(i)=(i-1)×(M(i)-1)+1

(14)

b(i)=i×(M(i)-1)+1

(15)

第i個窗口均值為：

m(i)=f(mean([a(i)…b(i)]))

(16)

調度電池充放電電功率的值為：

pb(i)=m(i)-mean(m)

(17)

圖1是按剩余調度段的標準差最小的原則取隨機量的變尺度均值。

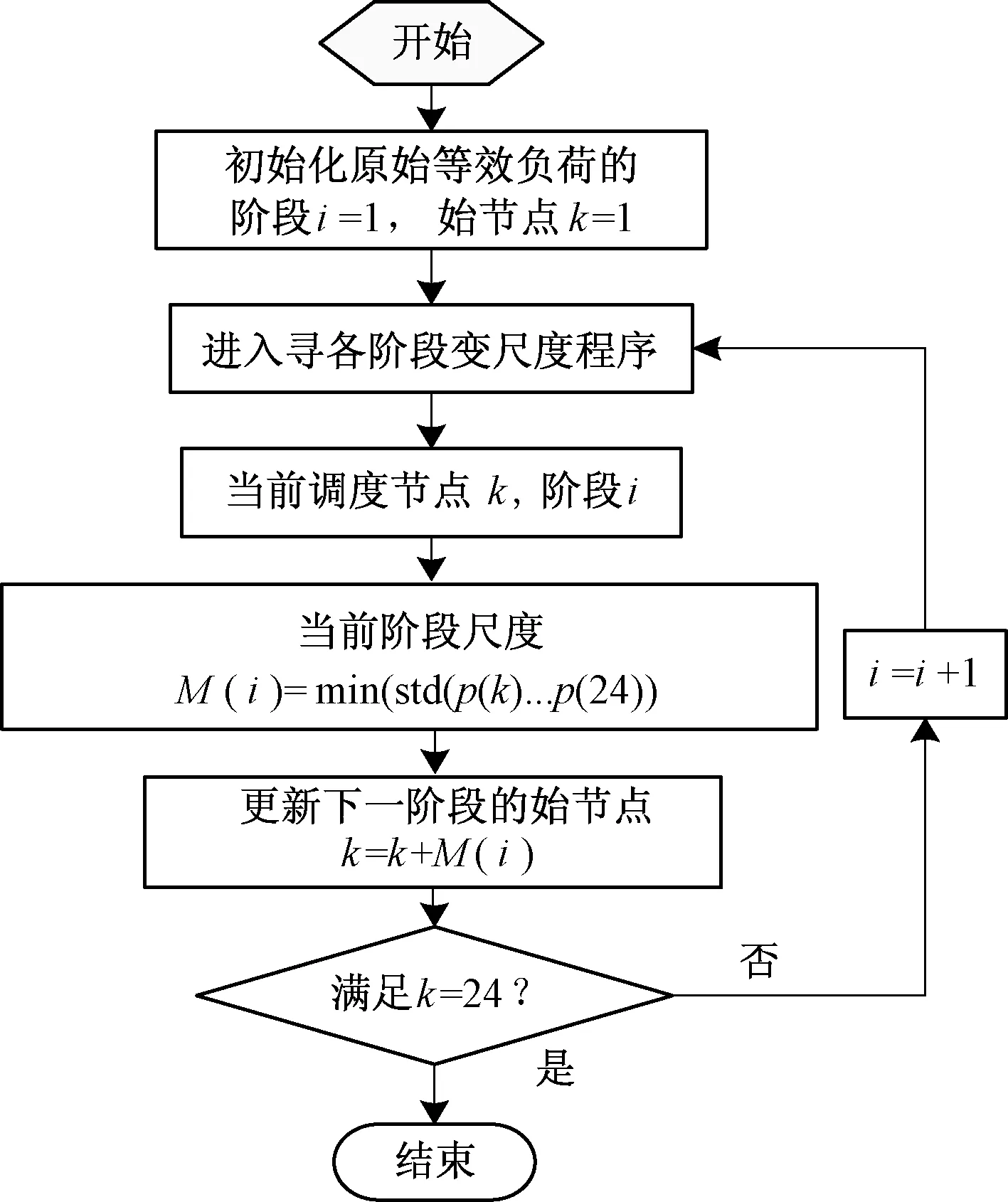
圖1 隨機量的變尺度窗口

2.3 電池充放電指令的生成

理想的調度目標是各個時段的窗口內，并網功率為一恒定值，即無波動性；所有相鄰時段的窗口并網功率波動性最小。因此電池的充放電指令應該為：當光伏功率變化為上升趨勢且大于各窗口均值的均值時，儲能系統的作用相當于將光伏功率“拉低”變化較為平穩的區間，因此儲能系統多數時間保持處于充電狀態，儲能系統充電能量變化表現為上升趨勢；當光伏功率變化為下降趨勢且小于各窗口均值的均值時，儲能系統的作用相當于將光伏功率“抬高”到變化較為平穩的區間，因此儲能系統多數時間保持處于放電狀態，儲能系統充電能量變化表現為下降趨勢[3]。則當按上述方法完全補償光伏功率波動時可求出儲能電池的最大容量。具體流程如下圖2所示。

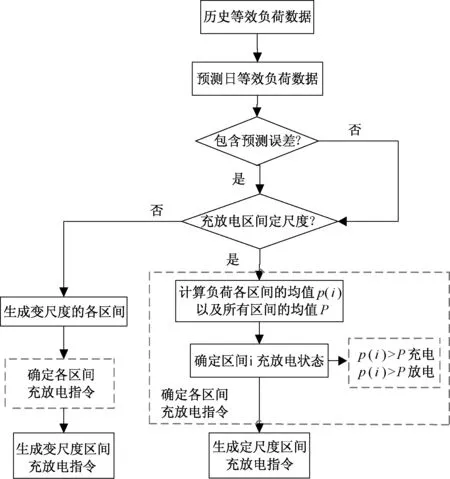
圖2 電池充放電指令的流程圖

2.4 相關約束條件

(1)功率平衡約束

在平抑隨機量X(本文是原始光伏功率)波動時，Y是經電池充放電調節后的光伏并網功率。設X為采樣頻率為5 min離散化的功率值，則在t時刻，可得原始光伏功率X與并網功率Y的關系如下式：

Y=X-pb

(18)

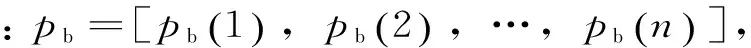
(2)充放電次數約束

當采用全部數據對應的同一個均值時，儲能充放電次數太頻繁，每5min都要變；即充放電次數約束決定了調度次數，即窗口個數。確定儲能系統充放電區間時，根據蓄電池組容量及最大充放電功率約束，結合負荷的峰谷時間段，確定一個或多個連續的充/放電區間，從而有效避免其頻繁充放電，延長蓄電池使用壽命；還能避免電池過度充/電，保護電池，此外，在峰谷時段充放電，可有效削峰填谷[4]。

(3)充放電最大功率約束

(19)

t時段的電池充/放電功率|pb(t)|最大不超過PESS，可通過調節總窗口個數改變。

(4)電池容量約束

為滿足平抑等效負荷功率波動的需要，儲能所需最大容量如下所示：

(20)

(21)

Et為一次充或放電后電池的電量。

(5)日充放電量約束

En=0

(22)

為使電池在每個調度日發揮相同的作用，需保持電池每日的充放電量之和為0，即每天始、末時刻電池的荷電狀態(StateofCapacity，SOC)相同。

(6)荷電狀態hSOC的定義及其相關約束

hsoc(t)=Qre(t)/Qmax

(23)

hsoc(t+1)=hsoc(t)+pb(t)×Δt

(24)

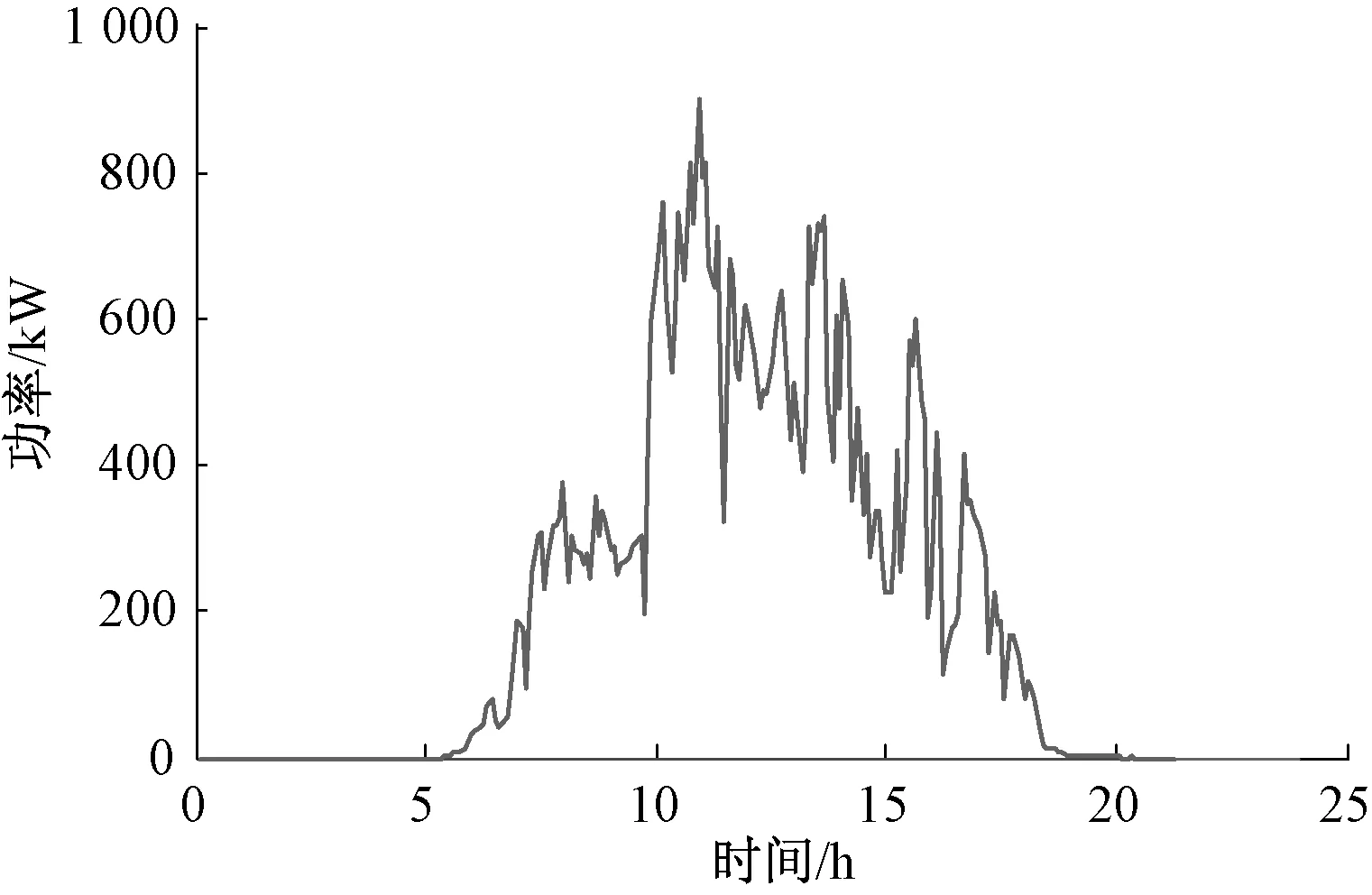
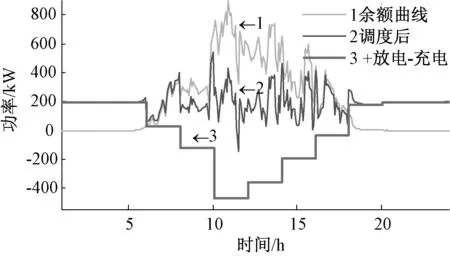
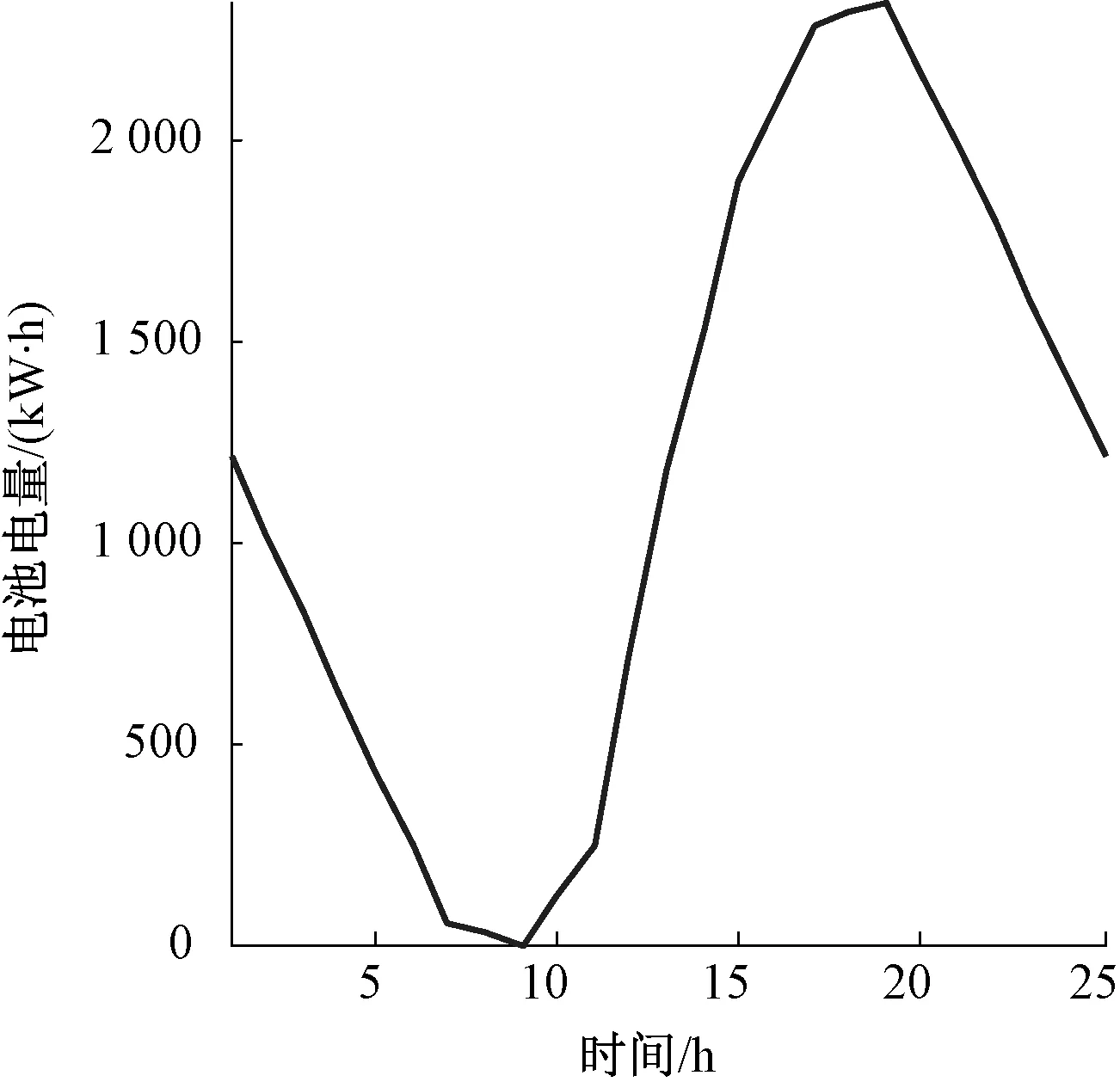
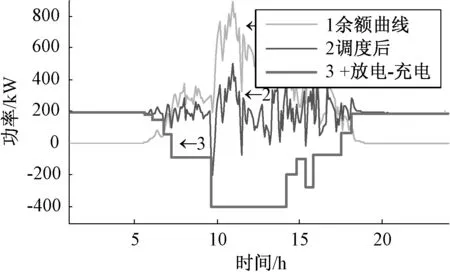
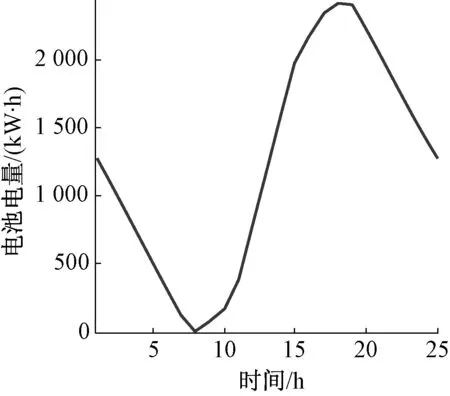
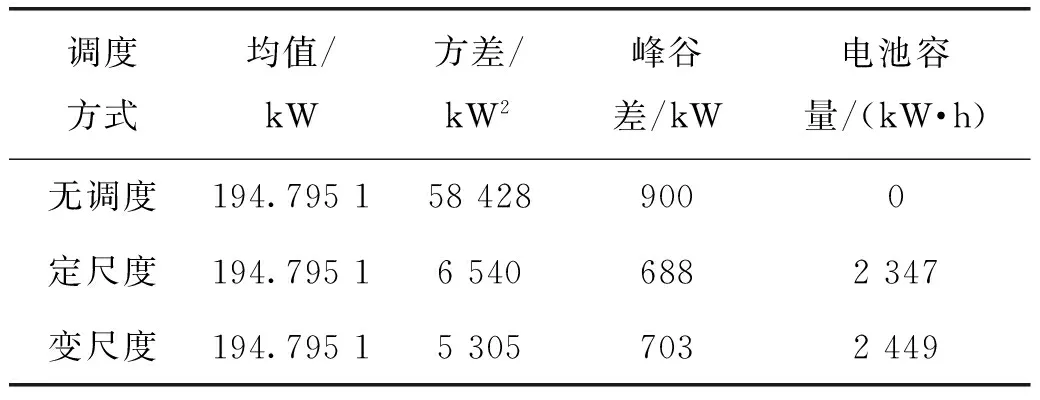
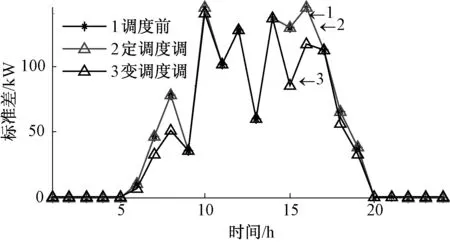
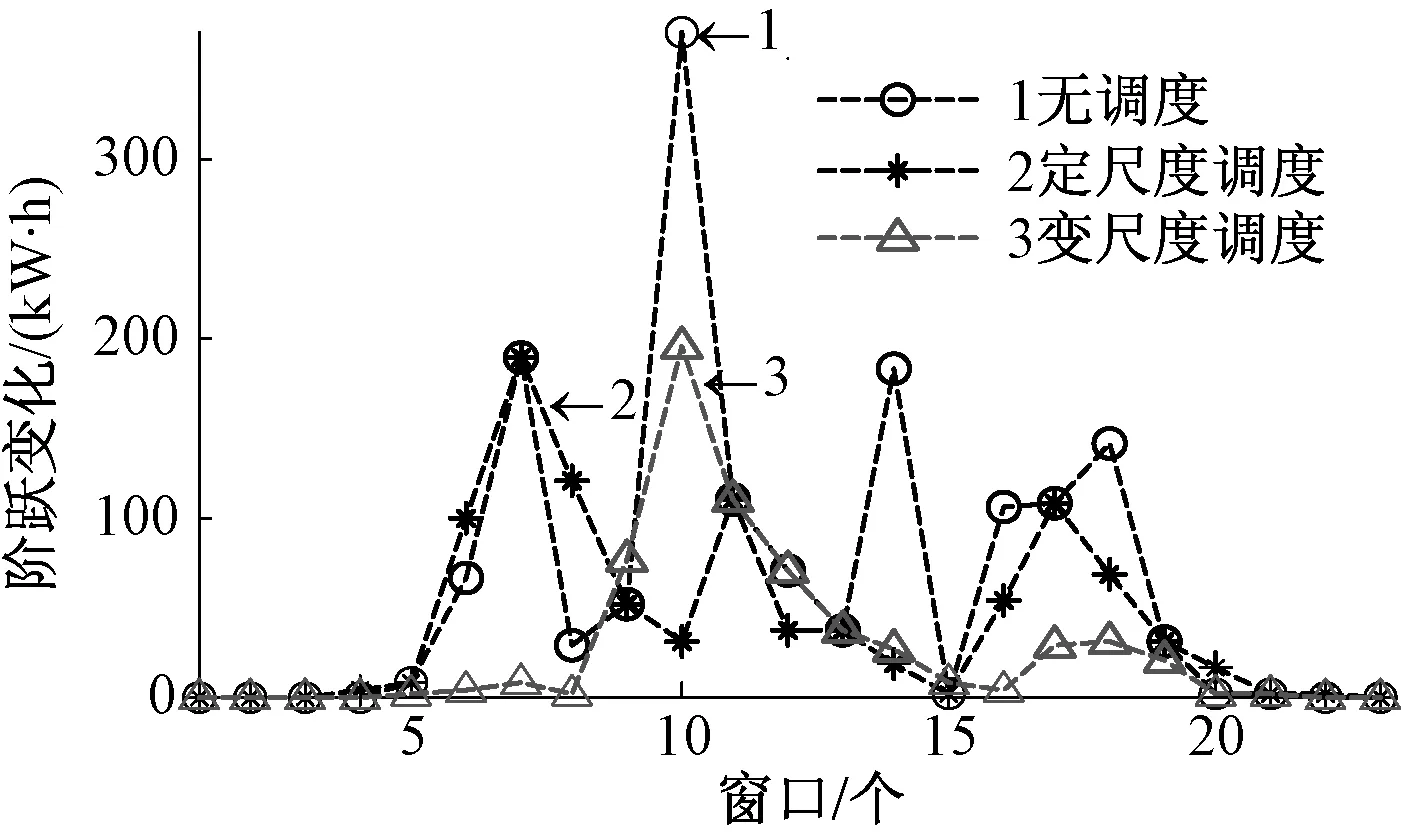
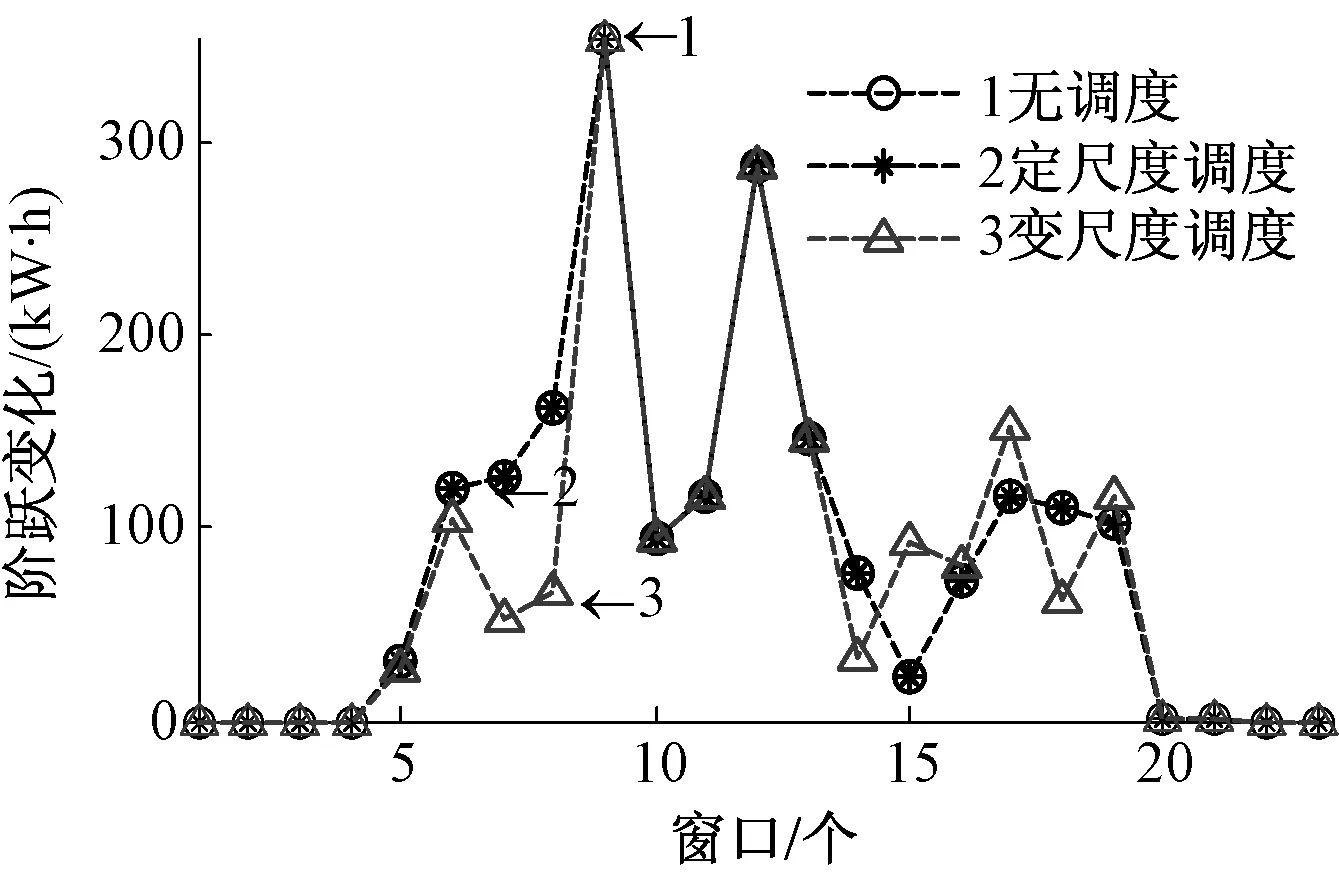
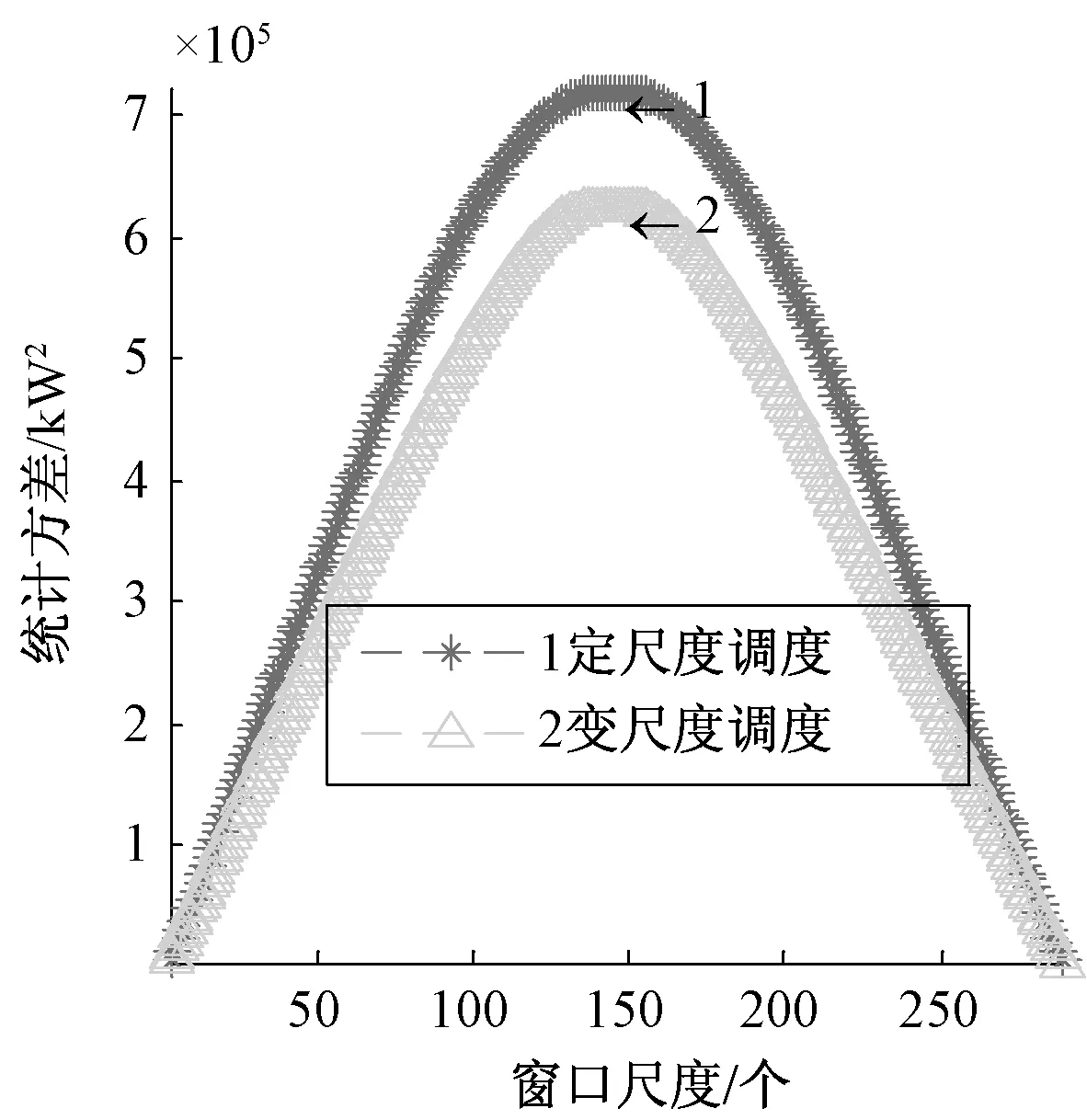
hsoc.max

(25)

式(23)中：用hsoc(t)表示電池t時刻的荷電狀態，即t時刻的電池剩余容量Qre(t)與其總容量Qmax的百分比；式(24)反映了相鄰時段電池荷電狀態的關系；式(25)則反映在任何時段都要滿足其荷電狀態的約束，對蓄電池來說，通常取hsoc.max=1，而考慮到電池過度放電對其壽命的不利影響，hsoc.min常取為 0.2。

3 算例

3.1 系統介紹

美國Ashland的15kW光伏電站[15]某典型日的光伏出力曲線如圖3所示。

圖3 光伏功率的波動性

本文設置一天調度次數n=12，即每個定尺度窗口的調度間隔Δt=2 h，變尺度限制最小尺度為 3個采樣點的2種調度方案。

3.2 調度效果

定尺度窗口調度電池的效果如圖4所示。電池在1～6,18～24時段放電；在6～18時段充電。每2 h保持同一功率進行充/放電，并且充電的功率與光伏功率幅值成正比。

電池電量變化如圖5所示。

圖4 定尺度12窗口的調度圖

圖5 定尺度12窗口的電池電量變化圖

變尺度窗口調度電池的效果如圖6～7所示。

圖6 變尺度12窗口的調度圖

圖7 變尺度12窗口的電池電量變化圖

與圖4相比，圖6對應的電池在充/放電時段間隔不等，但是總窗口數與圖4中的一致，均為12個。可見，電池作用是將曲線的均值抬高，但是并沒有改變其高頻分量，應該用可頻繁充放電的超級電容濾波進行平滑。

光伏功率在電池定、變尺度調度后一般波動性的比較如表1所示。

表1 光伏功率的的一般波動性

由表1可見，完全補償光伏功率波動時，在調度前后其均值保持不變；其一般波動性的不同指標在定、變尺度調度后的都有改善，并且在定、變尺度調度對儲能系統容量的要求沒有明顯區別[18]。

電池調度前，定、變尺度調度后光伏功率的多尺度波動性的比較如下，1 h內均值、標準差如下圖8、9所示。

圖8 等效負荷1 h均值對比

圖9 等效負荷1 h標準差對比

由圖可看出，光伏功率在電池定、變尺度調度后1 h均值變化都比調度前平滑很多；1 h 內波動性變尺度比定尺度調度后效果要好。

電池調度前，定、變尺度調度后光伏功率的1 h階躍變化率、M界定的1 h階躍變化率分別如圖10、11所示。

圖10 1 h階躍變化率

圖11 M界定的階躍變化率

定尺度調度并不能改變M界定的階躍變化率，即在圖11中無調度和定尺度調度的M界定的階躍變化率的曲線重合,因為在同一小時內減去相同的值,其極差不變。并且圖11的M界定的極差階躍變化率要比圖10對應的1 h階躍變化率要大。

電池調度前，定、變尺度調度后光伏功率的統計方差如圖12、13所示。

圖12 調度前、后統計方差對比

圖13 定、變尺度統計方差對比

由圖12可見，無論定、變尺度調度都在很大程度上改變了等效負荷的多尺度波動性，并且在圖13中比較，變尺度比定尺度的改善效果更為明顯。

4 結論

本文從衡量隨機量的波動性出發，對一般波動性、多尺度波動性進行闡述，在此基礎上，提出了定、變時間尺度窗口調度電池平抑光伏功率波動的方法。由于變窗口尺度調度法適度的考慮了數據的相關性，針對光伏功率波動性大的部分縮小調度尺度，波動性小的部分增大調度尺度，變尺度在考慮局部多尺度波動性的同時又照顧了整體的一般波動性，而定窗口尺度調度法是在一個方案里按同一個尺度調度，這樣處理數據時顯得呆板。最后用一個算例，驗證了所提方法的優越性，變尺度調度電池充放電在避免電池頻繁充放電的同時更能減弱光伏功率在并網時給配電網帶來的沖擊的問題。

[1]吳振威，蔣小平，馬會萌，等.多時間尺度的光伏出力波動特性研究[J].現代電力，2014，31(1):58-61.

[2]王磊.光伏發電系統輸出功率短期預測技術研究[D].合肥：合肥工業大學，2012.

[3]陳益哲.微網中分布式儲能系統的建模與控制研究[D].武漢：華中科技大學，2011.

[4]陳益哲,張步涵,王江虹，等.基于短期負荷預測的微網儲能系統主動控制策略[J].電網技術,2011,35(8):35-40.

[5]林少伯,韓民曉,趙國鵬,等.基于隨機預測誤差的分布式光伏配網儲能系統容量配置方法[J].中國電機工程學報,2013,33(4):25-33.

[6]鮑冠南,陸超,袁志昌，等.基于動態規劃的電池儲能系統削峰填谷實時優化[J].電力系統自動化,2012,36(12):11-16.

[7]丁華杰,宋永華,胡澤春,等.基于風電場功率特性的日前風電預測誤差概率分布研究[J].中國電機工程學報,2013,33(34):136-144.

[8]楊樹德,同向前. 風電功率波動特性描述方法比較研究[C]. 分布式發電、智能微電網與電能質量——第三屆全國電能質量學術會議暨電能質量行業發展論壇論文集,2013.

[9]李劍楠,喬穎,魯宗相，等.大規模風電多尺度出力波動性的統計建模研究[J].電力系統保護與控制,2012，(19):7-13.

[10]林衛星,文勁宇,艾小猛，等.風電功率波動特性的概率分布研究[J].中國電機工程學報，2012，32(1):38-46.

[11]李軍徽.抑制風電對電網影響的儲能系統優化配置及控制研究[D].華北電力大學(北京)，2012.

[12]李秋碩，肖湘寧，郭靜，等.電動汽車有序充電方法研究[J].電網技術，2012，36(12):32-38.

[13]韓海英，和敬涵，王小君，等.基于改進粒子群算法的電動車參與負荷平抑策略[J].電網技術，2011，35(10):165-169.

[14]張學清.風電預測、協同調調度及電網電壓安全評估研究[D].濟南：山東大學，2013.

[15]張佳偉.光伏并網發電系統短期發電功率預測研究[D].南京：南京信息工程大學，2013.

[16]楊愛民，張晨曦，文福栓，等.微網環境下的電動汽車換電站運營策略[J].華北電力大學學報：自然科學版，2013，40(4):19-26.

[17]朱銘，黃偉，郭佳歡，等.微網并網時的經濟運行研究[J].電網技術，2010，(34)：38-42.

Research on Battery Management to Reduce the Effect of Photovoltaic Power on Grid

Zhao Xiangyang, Wang Xingxuan

(School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China)

It is difficult to forecast, schedule and control photovoltaic power. However, energy storage system with the parallel operation of photovoltaic power device can be used to stabilize randomness of photovoltaic power on grid and minimize the impact on grid quality. This paper studies the battery management method to minimum photovoltaic power fluctuation when connected to the main grid. According to random quantity general and multi-scale volatility index, the battery charging and discharging control strategies based on the fixed window size and varied window size were proposed. By simulation, the optimization effect and the storage system capacity were compared. The results indicate that the variable window size has better stabilization than fixed window size.

photovoltaic grid-connected; battery management; fixed/varied temporal scales

2015-07-06。

趙向陽(1967-)，男，副教授，研究方向為微電網光伏發電及調度、電氣檢測及其信息技術。通信作者：王杏玄，E-mail:1064836024@qq.com。

TM743

A

10.3969/j.issn.1672-0792.2015.09.008