一種改進的功率比值法載噪比估算算法

傅金琳，趙子陽，李醒飛

（1. 天津大學 精密儀器與光電子工程學院，天津 300072；2. 天津航海儀器研究所，天津 300131）

一種改進的功率比值法載噪比估算算法

傅金琳1,2，趙子陽2，李醒飛1

（1. 天津大學 精密儀器與光電子工程學院，天津 300072；2. 天津航海儀器研究所，天津 300131）

針對GPS載噪比估算方法功率比值法中出現的導航電文翻轉敏感問題，提出改進算法。改進算法根據對I路符號判決結果對導航數據位進行預測，基于預測結果消除載噪比估算中導航電文的影響，達到消除導航電文翻轉影響的效果。理論計算分析證明該算法能夠提高載噪比的估算精度，提升載噪比的更新率，從而提升系統的靈敏度與穩定性。分別對改進算法載噪比估算精度、抵抗導航電文翻轉能力、M取值、載噪比更新率等幾個方面進行了仿真驗證，證明理論分析的正確性。

功率比值法；導航電文翻轉；載噪比；更新率

在 GPS接收機中信號捕獲門限與載噪比直接相聯[1]，信號跟蹤環路鎖定檢測和接收機性能預估也都依賴于載噪比測定。當載噪比低于30 dB·Hz時，跟蹤環路鎖相環的跟蹤錯誤將快速增加[2]。目前接收機通常將載噪比作為 GPS測量值輸出的一部分[3-4]，可見對載噪比的估算對GPS接收機整體性能至關重要。

鑒于GPS載噪比指標的重要性，目前相關估計法研究比較多，主要的載噪比估算方法有增加噪聲通道法[5]、方差求和法[6]、實信號復噪聲法[7]以及窄帶寬帶功率比值法(PRM：Power Ratio Method)[8]等。其中PRM算法由于復雜度適中且有較高的估算精度，得到較為廣泛的使用，如文獻[9]研究了自適應調整估計時間的PRM載噪比估算方法。然而以往研究的PRM算法中，會出現因導航電文翻轉而導致算法性能下降，針對這個問題，本文提出一種改進的不受導航電文翻轉影響的載噪比估算法。

1 信號模型

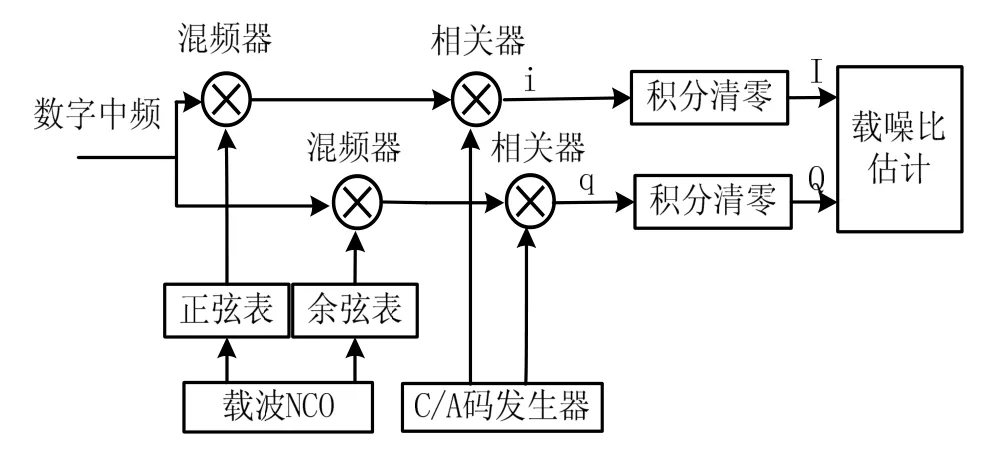
圖1給出了GPS接收機跟蹤環路中與載噪比估算相關的部分原理框圖。

從圖1中可知，GPS數字中頻經過混頻器和相關器后得到信號i、q：

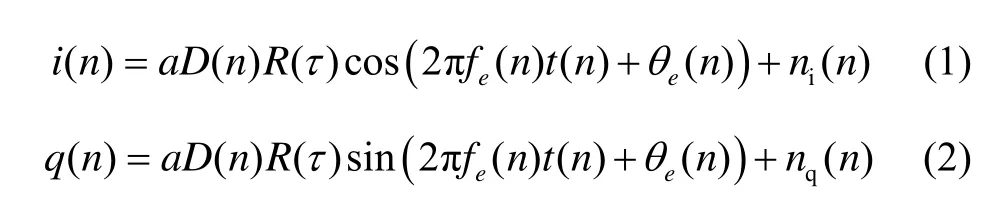
式中：D( n)為正負1的數據電平值，τ為復制的C/A碼與接收到的衛星 C/A碼之間的相位差，θe(n)為復制載波與接收到的載波相位差，ni( n)和nq( n)分別為i、q兩路的噪聲。i、q信號經過積分清零的表達式為

將式(9)代人式(5)與式(6)可得：

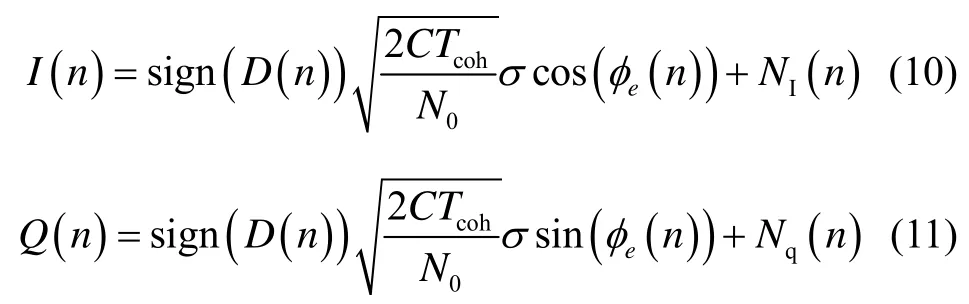
式中：sign(x)表示取x的符號。

對式(10)和式(11)進行歸一化處理得：

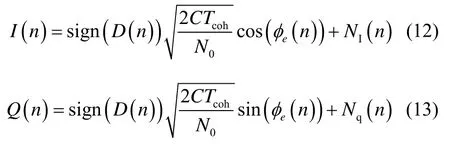
經過歸一化后，以上兩式中的噪聲服從均值為0，方差為1的正態分布。

2 傳統PRM功率計算

傳統 PRM估算法的前提是接收機能夠獲得信號和噪聲的功率和，并且能夠獲得不同噪聲帶寬上的信號和噪聲功率和。不同噪聲帶寬上信號和噪聲功率和的比值能夠用來估算載噪比。分別用WBP( k)和NBP( k )表示帶寬為1/Tcoh的寬帶功率和帶寬為1/MTcoh的窄帶功率，M為累加的次數，則有

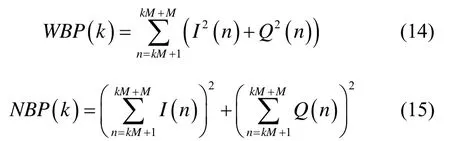
一般來說，Tcoh的取值為1 ms。傳統PRM估算法中要求MTcoh長的數據在同一個比特內，即M小于20，以保證通過式(15)算出的是窄帶功率。忽略高斯噪聲，式(15)展開為

式中：（sign(D(n))）2=1。

然而，就算M小于20，MTcoh時長的數據也可能不在一個比特內。結合式(12)、(13)和(15)可知，如果MTcoh時長不在一個比特內，那么窄帶功率的計算與導航電文的正負有直接的關系。假設MTcoh長的數據內在M1Tcoh長的數據為正，而后導航電文發生翻轉，即長數據為負，那么式(15)重寫為

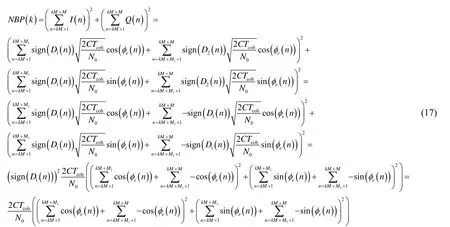
φe(n)為載波相位誤差，一般比較小。對比式(16)和式(17)可知：如果在一次計算中出現導航電文的翻轉，那么由式(17)計算的功率將將要小于實際的窄帶功率值，不再是窄帶功率；當有一半電文發生翻轉，即導航電文的翻轉位置出現在MTcoh的中間位置，則能導致窄帶功率的估算值近似為0。

3 改進載噪比估算法

根據上面的分析可知，導航電文的翻轉導致窄帶功率的估算與真實值存在較大的誤差，為此在改進的載噪比估算法中首先對導航電文進行估算，而后根據導航電文估算結果去除其對窄帶功率估算的影響。

在GPS環路跟蹤過程中，通過對I之路數據符號的判斷進行導航電文的解調，即

導航電文也是跟蹤環路中的輸出結果之一，這里只是再將其用于對載噪比的估算，因此不會增加系統的復雜度。改進載噪比估算法中窄帶功率的計算公式重寫為

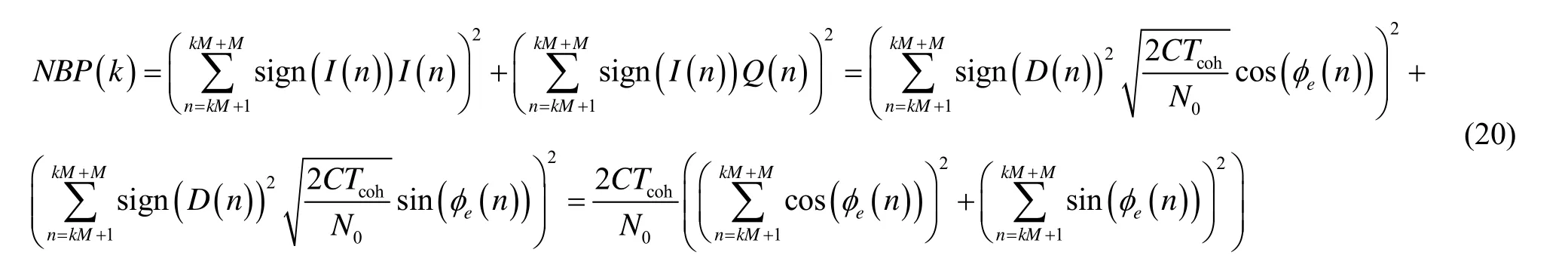
從式(20)可知，通過引入I路符號估算結果，窄帶功率估算結果不再受到導航電文的影響，即導航電文翻轉不再影響窄帶功率的估算。

將寬帶功率與窄帶功率進行單位化，得到它們的比值Pnw(k)為

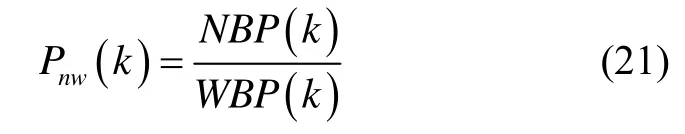
寬帶功率與窄帶功率的數學特征為[10]

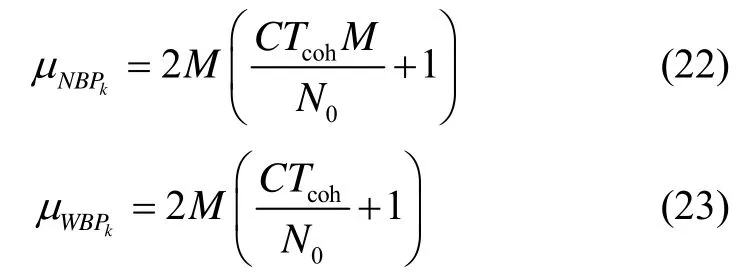
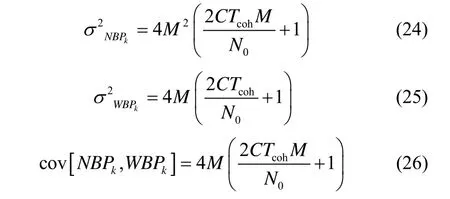
由概率基本公式可得：

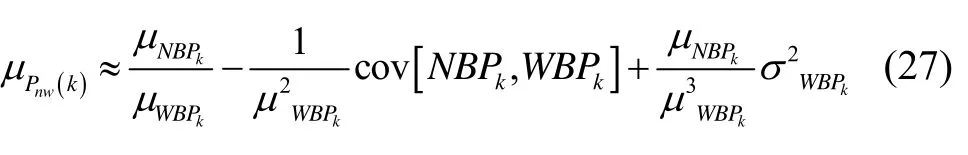
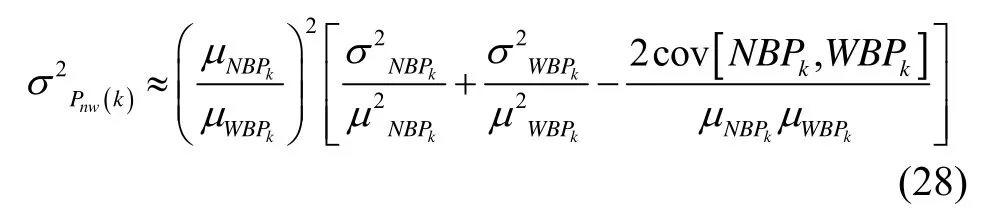
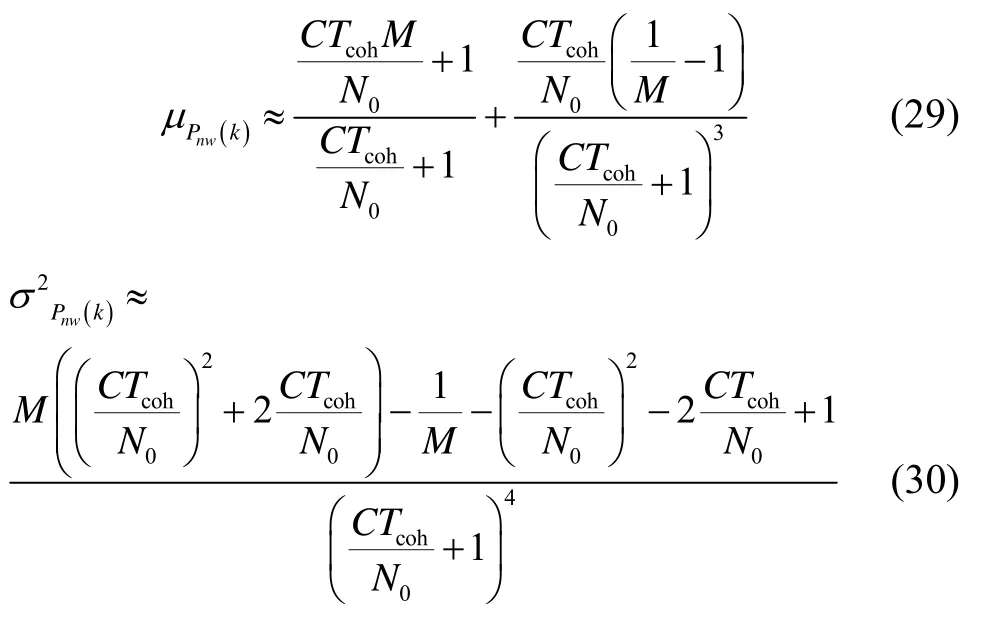
3.1 強GPS信號情況

當存在強GPS信號時，即存在可見GPS衛星時，載噪比一般為40～50 dB·Hz，即數量級為104到 105，因此式(29)近似等于

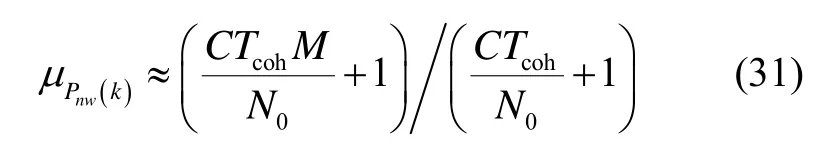
為了降低比值Pnw（k）中的噪聲量，通常對 K個Pnw(k)的值進行平均得到其平均值μp：

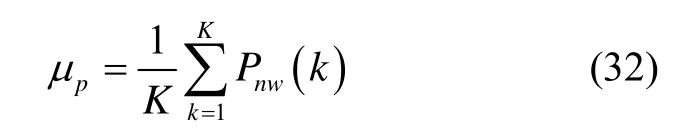
從而得到以赫茲為單位的載噪比：

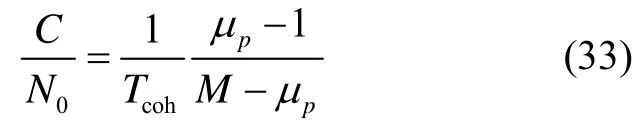
通過式(33)計算的載噪比估算誤差的均方差為[1]

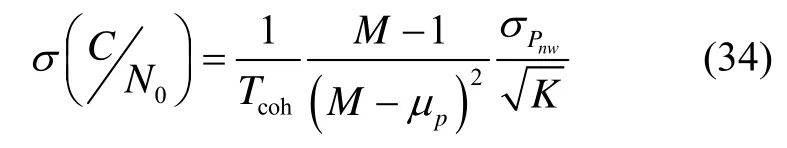
結合式(30)、式(33)與式(34)可得：

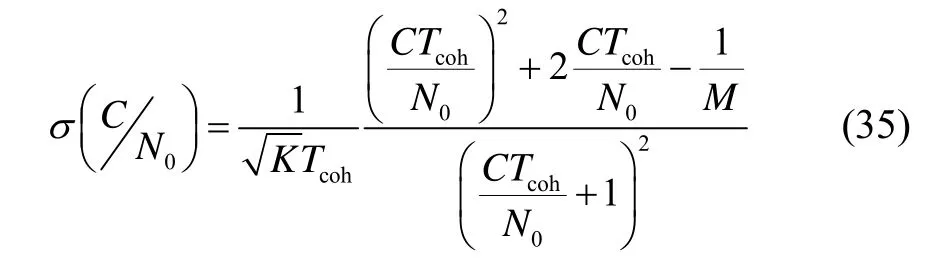
從式(35)與可知，增大M有利于減小載噪比的估算誤差。在傳統的 PRM載噪比估算法中，為了避免導航電文翻轉對載噪比估算值的影響，M的值通常不大于20，而在改進的算法中，由于去除了導航電文的影響，M的值可以取得很大。由于I路實部符號估算本來就是接收機信號處理的一部分，因此改進算法沒有增加系統的復雜度。也就是說改進的算法在不增加系統復雜度的情況下，使得M的取值可以任意大，從而減少載噪比的估算誤差。此外，在傳統 PRM中，如果存在導航電文翻轉，那么占比小的符號位對應的信號功率相當于噪聲，即增大了噪聲功率減小了信號功率，因此常常通過增大K來降低噪聲量，導致載噪比的更新率不能做的很高。在高動態運動時，低的載噪比更新率可能不能及時反映信號的質量，從而導致定位誤差很大。改進的算法不存在此部分噪聲，因此其更新率能夠做到很高，能夠及時反映信號的質量以便接收機進行正確的判決。

3.2 弱GPS信號情況

當GPS信號較弱，即不存在可見GPS衛星時，極限情況假設載噪比為0，式(29)與式(30)重寫為

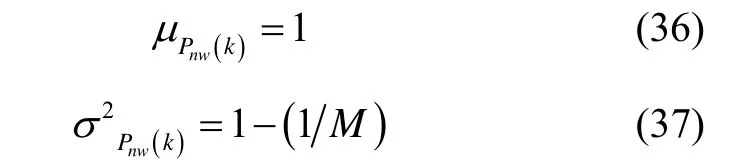
從式(37)可知，增加M能夠大大減小GPS信號不存在時載噪比的估算誤差。

4 算法驗證效果與性能比對

分別基于GPS L1模擬中頻信號源和實測的中頻信號進行仿真驗證，著重點為考察導航電文跳變時對載噪比估算算法的影響，因此模擬中頻信號源采用固定的多普勒頻移，實測數據的觀測點為固定，主要考察跟蹤環路進入穩態后估算的載噪比。本文中每次的相干累積時間為1 ms，即Tcoh=1 ms。下面分別從算法估算精度、改進算法抵抗導航電文翻轉能力、M取值、載噪比更新率等幾個方面進行仿真驗證，以證明改進算法的優勢。

4.1 模擬中頻信號載噪比估算

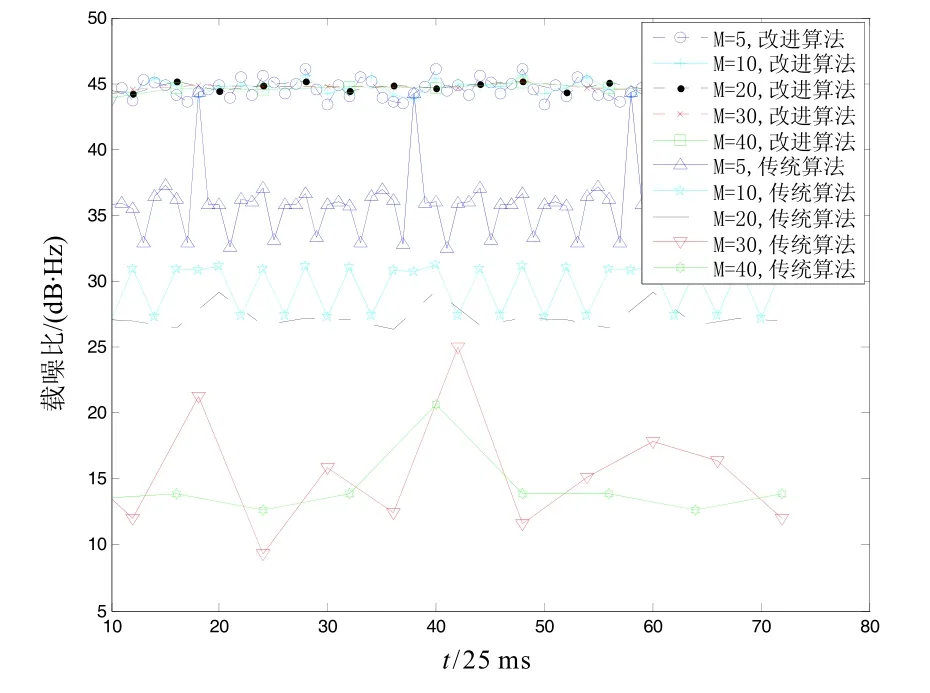
圖2 不同M取值時兩種算法估算結果Fig.2 Estimation results of two algorithms with different M values

模擬中頻信號的載噪比為45 dB·Hz，分別采用傳統PRM方法與改進算法對載噪比進行估算。圖2給出了K=5時，M取值不同時兩種算法的估算結果。從圖2中可以看出，在傳統PRM估算中，當M取值較大時，其估算性能嚴重受到導航數據位翻轉的影響，如當M取40時，估算的載噪比大多不到15 dB·Hz，這個值一般情況下就認為環路失鎖了，而實際的載噪比為45 dB·Hz，可見采用傳統PRM估算載噪比將導致接收機給出錯誤的判斷。當M取值較小時，由于受到導航數據位翻轉影響減少，傳統 PRM估算性能有所提高，但與實際值還是存在一定的差距。為了表達更加清楚，圖3只給了圖2中改進算法估算結果。從圖3中可以看出，不論M取何值，改進算法都能對載噪比進行正確估算。當M取值小時，估算的載噪比波動比較大；當M取值較大時，能減小載噪比估算的波動性，即增大M能夠改善載噪比的估算性能。

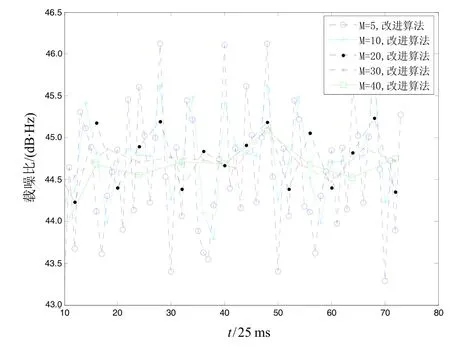
圖3 不同M取值時改進算法估算結果Fig.3 Estimation results of the improved algorithms with different M values

4.2 實測數據載噪比估算

4.2.1 抵抗導航電文翻轉驗證

圖4 給出了M=10，K=2時，傳統PRM算法與改進算法對載噪比的估計結果，即載噪比的更新率為50 Hz。為了對比，該圖還給出了增加噪聲通道法估算[6]的載噪比，增加噪聲通道法估算的載噪比理論上稍大于實際值。從圖4中可以看出，傳統PRM算法對載噪比估算結果的波動比較大，在29 dB·Hz到44 dB·Hz間跳變，這極有可能導致接收機將環路誤判為失鎖。產生這么大波動的原因是每次估算的10 ms的數據不在一個導航數據位，且相鄰的導航數據位存在跳變。采用改進的算法后，載噪比的估算基本在42.5 dB·Hz至44 dB·Hz間，載波比輸出較為穩定，沒有受到導航電文跳變的影響，這時接收機能夠正常穩定工作。對比增加噪聲通道法的載噪比估算結果，再次表明改進算法相比傳統算法估算結果更加準確。

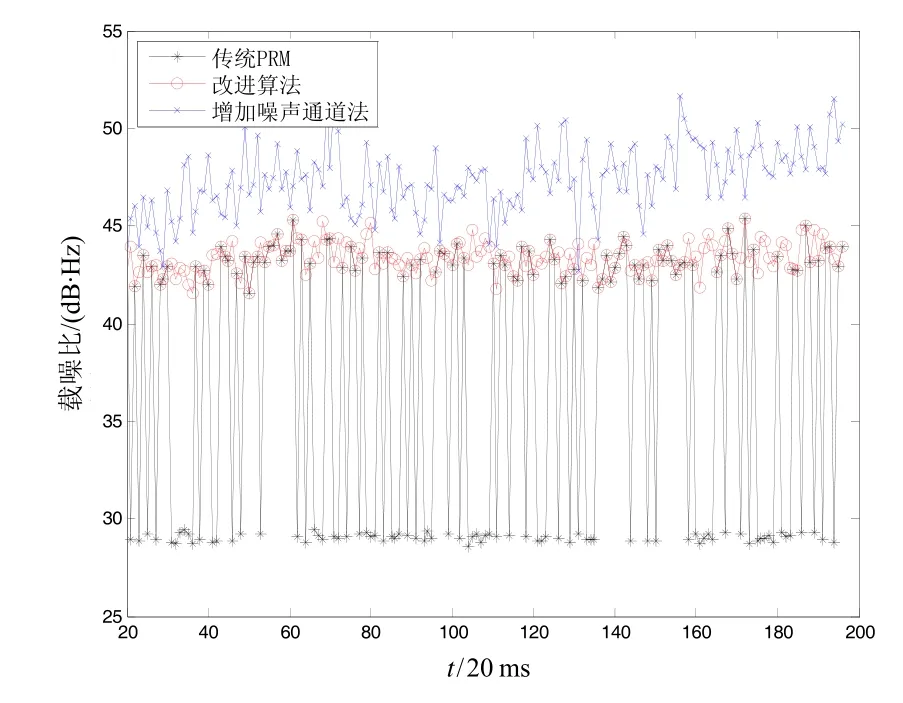
圖4 M=10, K=2算法性能比較Fig.4 Comparison on different algorithms’ performances when M=10, K=2

4.2.2 M取值驗證

圖5給出了載噪比更新率為2.5 Hz時，不同配置下不同載噪比估算方法的估算結果。從圖5中可以看出，當M取值比較大時，在傳統PRM中，由于導航電文的跳變使得窄帶功率的累加值嚴重下降，從而導致估算的載噪比嚴重失真。如果此時采用傳統的PRM估算法，將導致接收機不能正常工作。采用改進算法對載噪比進行估算時，M取200與80都能得到近似準確的載噪比，可見，改進算法中M的取值不受限制。

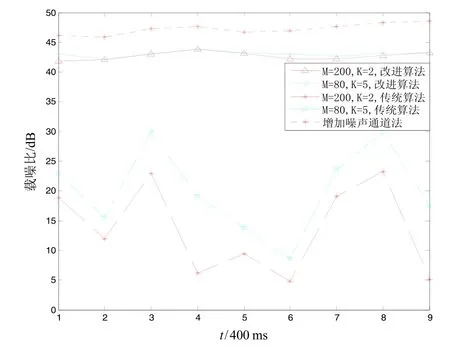
圖5 更新率2.5 Hz算法性能比較Fig.5 Comparison on different algorithms’ performances when update rate is 2.5 Hz

4.2.3 更新率驗證

下面給出M=5，K分別為2、10、20、40、80、160時，采樣傳統PRM算法與改進算法對載噪比的估算結果。為了保證圖像清晰，將K=2時的載噪比估算結果單獨放在圖6中，K=10, 20的載噪比估算結果放在圖7中，將K=40, 80, 160的載噪比估算結果放在圖8中。從圖6中可以看出，當更新率很高時，傳統PRM的估算結果存在比較大方差，估算的載噪比最低不足30 dB·Hz，這個值有些接收機就認為環路失鎖了，可見估算的載噪比不能很好地反映真實值，不能正確反映信號的真是質量，將影響接收機的正常工作。對比圖7與圖8可知，提高K能夠改善傳統PRM的估計性能，但這是以犧牲載噪比的更新率為代價的。從圖6中可知，改進算法雖然在K值較小時存在波動，載噪比在42 dB·Hz到47 dB·Hz，可見波動范圍較小，在可接受的范圍內，能夠正確反映接收到的信號的質量。對比圖7和圖8可知，增大K也能提升改進算法載噪比的估算精度，這與理論分析結果一致。

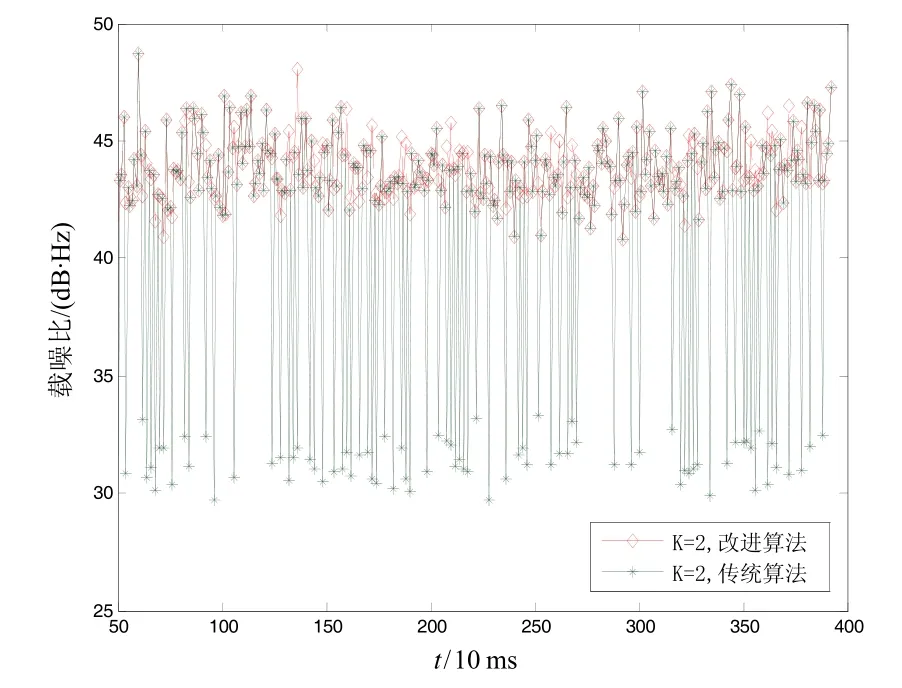
圖6 K=2時兩種算法載噪比估算結果Fig.6 CNR estimation results of two algorithms when K=2

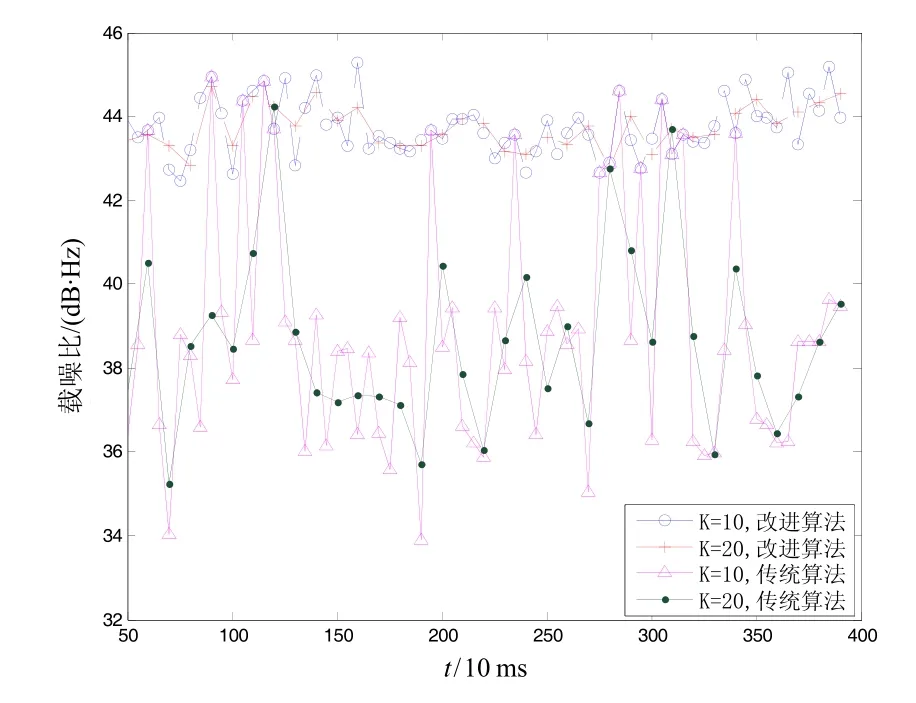
圖7 K=10, 20時兩種算法載噪比估算結果Fig.7 CNR estimation results of two algorithms when K=10, 20

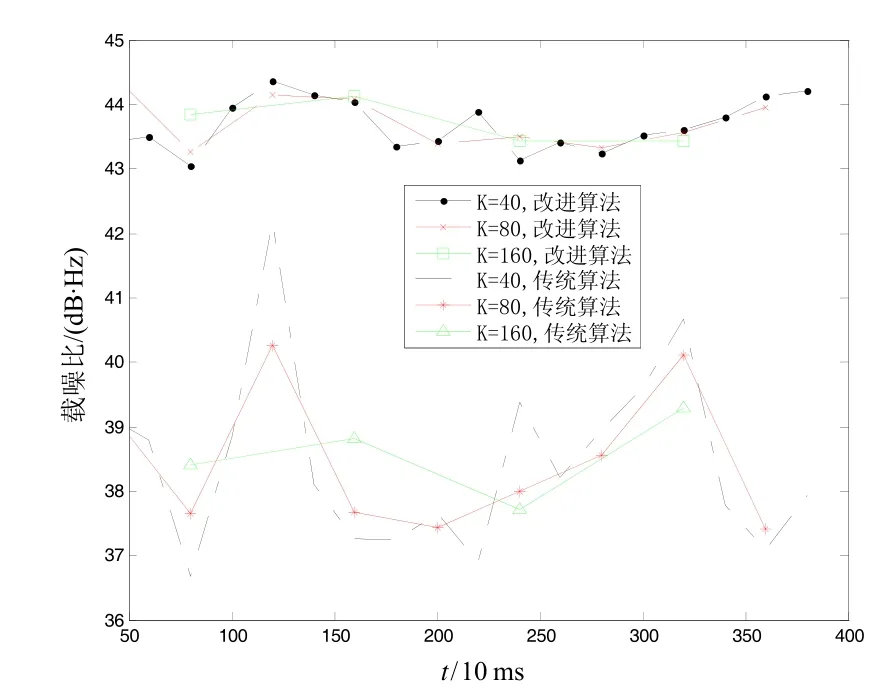
圖8 K=40, 80, 160時兩種算法載噪比估算結果Fig.8 CNR estimation results of two algorithms when K=40, 80, 160

4.3 小 結

從上面的仿真驗證結果可以看出，改進算法與傳統PRM算法相比：① 改進算法具有更高的載噪比估算精度；② 改進算法載噪比估算不會受到導航電文翻轉的影響；③ 改進算法 M 取值不受限，能夠取無限大；④ 改進算法具有更高的載噪比更新率。

5 結 論

本文提出了基于傳統 PRM的改進算法，該算法在 GPS強信號時能夠規避傳統算法對導航電文翻轉敏感的缺陷，避免傳統算法中由于導航電文翻轉帶來的噪聲干擾，提高了載噪比的估算準確度。當GPS弱信號時，改進算法通過加大M值，能夠減小估算誤差。由于在改進算法中，M值能夠任意選取，因此改進算法的載噪比的更新率能夠做得很高，從而實時對接收機接收到的信號質量進行判決，提升了接收機的性能。

（References）：

[1] 曾慶喜, 唐琳琳, 王慶, 等. GPS軟件接收機寬載噪比載波頻率精確捕獲策略[J]. 中國慣性技術學報, 2013, 21(4): 500-505. Zeng Qing-xi, Tang Lin-lin, Wang Qing, et al. Acquisition of fine carrier frequency under wide carrier-to-noise ratio in GPS software receivers[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 500-505.

[2] 文力, 謝躍雷, 紀元法, 等. 基于最大似然法的GPS弱信號載噪比估計算法[J]. 桂林電子科技大學學報, 2014, 34(5): 406-410. Wen Li, Xie Yue-lei, Ji Yuan-fa, et al. Weak GPS signal C/N0estimation algorithm based on maximum likelihood method[J]. Journal of Guilin University of Electronic Technology, 2014, 34(5): 406-410.

[3] Yang Yong-wen, Weerackody V. Estimation of link carrier-to-noise ratio in satellite communication systems [C]//The 2010 Military Communications Conference –Unclassified Program – Systems Perspectives Track. 2010: 1552-1557.

[4] 蔣君偉, 段曉輝, 林陽. GPS信號載噪比估計算法的研究[J]. 北京大學學報(自然科學版), 2009, 45(3): 409-414. Jiang Jun-wei, Duan Xiao-hui, Lin Yang. The research of estimation method for GPS C/N0[J]. Acta Scientiarum Naturalium University Pekinensis, 2009, 45(3): 409-414.

[5] Groves P. GPS signal to noise measurement in weak signal and high interference environments[C]//ION GNSS. Long Beach, CA, 2011.

[6] Sharawi M S, Akos D M, Aloi D N. GPS C/N0 estimation in the presence of interference and limited quantization levels[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 43(1): 227-238.

[7] Emanuela F, Marco P, Letizia L P. Low complexity carrier-to-noise ratio estimators for GNSS digital receivers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 420-437.

[8] Balaei A, Dempster A, Barnes J. A novel approach in the detection and characterization of CW interference on the GPS signal using receiver estimation of C/No[C]// Proceeding of IEEE/ION PLANS. 2012, 1120-1126.

[9] 何文濤, 徐建華, 葉甜春. GPS弱信號的自適應載噪比估計算法[J]. 電子技術應用, 2011(6): 111-114. He Wen-tao, Xu Jian-hua, Ye Tian-chun. Adaptive C/N estimation method of GPS weak signal[J]. Application of Electronic Technique, 2011, 6: 111-114.

[10] Parkinson B, Spilker J, Axelrad P, et al. Global positioning system: theory and applications[M]. American Institute of Aeronautics and Astronautics, 1996.

Improved power ratio method of carrier-to-noise ratio estimation algorithm

FU Jin-lin1,2, ZHAO Zi-yang2, LI Xing-fei1
(1. Tianjin University School of Precision Instrument and Opto-electronics Engineering, Tianjin 300072, China; 2. Tianjin Navigation Instruments Research Institute, Tianjin 300131, China)

In view that the power ratio method in carrier-to-noise ratio (CNR) estimation is sensitive to navigation data transition, an improved algorithm is proposed to solve this problem. In this improved algorithm, the navigation data are predicted according to the judgement of the path I’s sign, then the effects of navigation on CNR estimation are eliminated based on these predicted results, which makes it immune from the effects of the navigation data transition. Theoretical analysis is made on the proposed algorithm, which demonstrates that it can improve the CNR estimation accuracy and increase the update rate, therefore improving the system sensitivity and stabilization. Simulations are made on the estimation accuracy of the improved algorithm, the ability to resist the navigation data transition, the value of M, and the update rate of CNR, and the results verify the conclusions of the theoretical analysis.

power ratio method; navigation data transition; carrier to noise ratio; update rate

U666.1

：A

2015-06-03；

：2015-09-24

船舶預研支撐技術基金項目（14JZ3.9.2）

傅金琳（1984－），女，博士后，高級工程師，研究方向為綜合導航技術。E-mail：linkimf@163.com

1005-6734(2015)05-0642-06

10.13695/j.cnki.12-1222/o3.2015.05.015