間隙環流對核電主泵電機轉子振動的影響

曲大莊， 金 樂， 周 全， 李夢啟， 賈 鑫

（1.國家核電技術公司，北京100029；2.哈爾濱動力裝備有限公司，哈爾濱150066）

近年來，大型核電主泵電機多采用水為內部冷卻介質，如屏蔽電機和濕繞組電機.與傳統置于空氣中的主泵電機不同，由于電機定轉子之間充滿了冷卻水，當電機高速旋轉時，轉子表面將帶動冷卻水隨轉子一起轉動形成周向間隙環流，會對轉子的振動產生一定的附加影響.鑒于核安全的重要性，深入研究這種間隙環流對核電主泵電機轉子振動產生的附加影響，對核電站安全可靠運行有十分重要的意義.

通常研究間隙環流對轉子振動的影響主要包含兩方面的工作：一是間隙環流的動力學特性；二是這種動力學特性對轉子振動的影響.國外學者［1－4］在該領域無論從理論建模還是試驗驗證均取得了一些有價值的研究成果并應用于工程實踐，國內學者［5－8］近年來在該領域也進行了非常有益的研究和探索，豐富并推動了該領域的發展.

對于間隙環流的動力學特性，已取得的研究成果主要是通過能量守恒及攝動方法，把間隙環流對轉子振動的影響以附加質量矩陣、阻尼矩陣和剛度矩陣的形式轉化為作用在轉子上與轉速和結構參數密切相關的流體激勵載荷.對于這種動力學特性對轉子振動的影響，雖然已有許多研究成果，但針對轉子振動穩定性的邊界條件及渦動頻率的改變、轉子振動質量不平衡穩態響應振幅變化以及相應的臨界轉速等的研究還不夠完善，需要進一步深入探討.

筆者根據文獻［1］中對間隙環流動力學特性的研究成果，結合水冷卻核電主泵電機轉子的結構特點，以兩端簡支的單圓盤轉子為振動分析模型，研究了間隙環流對核電主泵電機轉子振動的影響.利用Hurwitz判據和振動系統復特征值方法給出了轉子振動穩定性的邊界條件以及渦動頻率的改變；通過解析求解轉子振動質量不平衡穩態響應，得到了轉子穩態振幅的變化依據以及相應的臨界轉速.借助復模態理論［9］和有限元分析方法，對一臺實際核電屏蔽電機主泵的轉子振動問題進行了數值模擬，為進一步深入研究間隙環流對核電主泵電機轉子振動影響的機理提供了理論依據.

1 間隙環流動力學特性及轉子振動方程

Antunes等［1］對圖1所示浸沒在流體中的轉子進行了比較深入的研究.根據流體在定轉子間隙中周向環流的連續性和力矩平衡，給出了單位長度上間隙環流沿轉子周向的壓力分布.

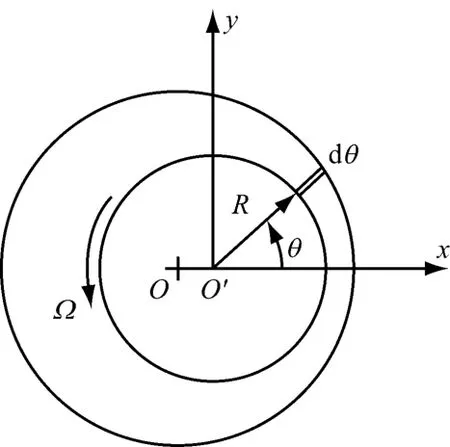
圖1 定轉子間隙環流Fig.1 Annular flow around stator

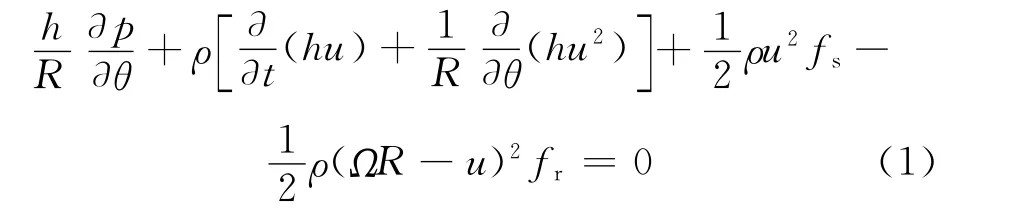
式中：ρ為流體質量密度；R 為轉子半徑；h 為定轉子間 隙；u 為 環 流 平 均 速 度；Ω 為 轉 速；fs、fr分 別 為定、轉子表面與流體的摩擦因數.

對于大多數無初始安裝偏心（ε0＝0）的情況，利用攝動法得到壓力分布的零階解

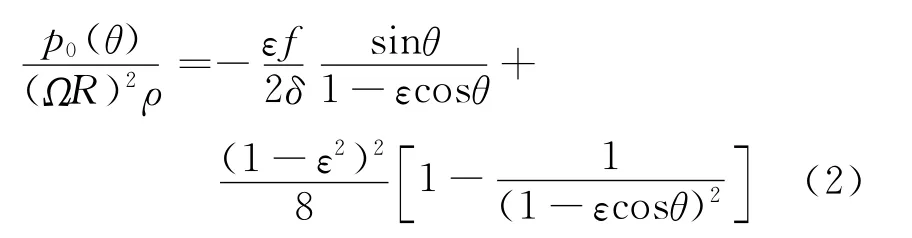
式中：ε為轉子偏心率；δ＝h／R，為定轉子間隙比.

通過式（2）可以看到，間隙環流的壓力分布形式在很大程度上取決于間隙比δ的數值.圖2給出了間隙環流的壓力分布.由圖2可知，對于較小的間隙比，式（2）表現出類似流體滑動軸承［10］的雷諾效應；但隨著間隙比的增大，式（2）則逐漸表現出伯努利效應，它使轉子振動位移導致間隙減小側的流速增大而壓力降低，使轉子振動位移進一步增大，結果出現轉子振動失穩的現象.

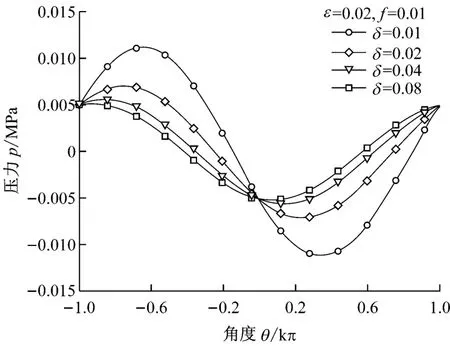
圖2 間隙環流壓力分布Fig.2 Pressure distribution of annular flow

當轉子在軸心位置發生小擾動時，對式（2）壓力分布在坐標x、y 方向的2 個分量沿轉子周向進行積分，可得到作用在轉子上由間隙環流產生的流體載荷［1］

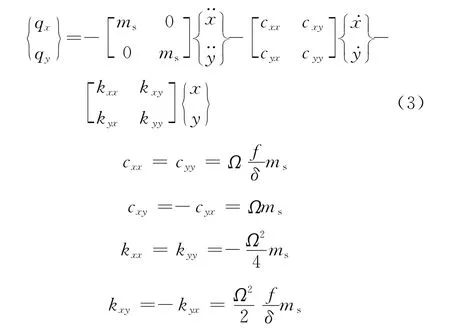
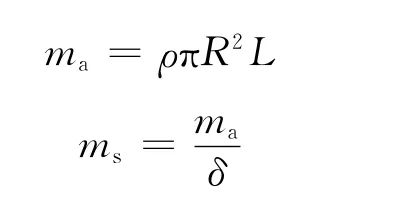
式中：ms為流體附加質量；L 為轉子長度；ma為間隙環流的總質量.

為從機理上進行研究，可略去結構阻尼，將核電主泵電機轉子振動問題簡化成兩端簡支的單圓盤轉子，在質量不平衡載荷以及式（3）流體載荷的聯合作用下，由振動理論［11］直接得到轉子振動的微分方程

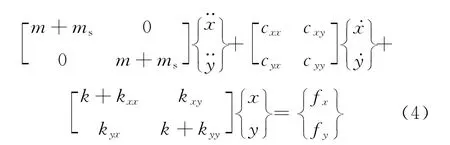
式中：m 為轉子質量；k 為彈簧剛度；｛fxfy｝T為不平衡質量載荷.

由式（4）可見，間隙環流的動力學特性是以附加質量ms、附加阻尼cij和附加剛度kij（i，j＝x，y）的形式對核電主泵電機轉子振動產生附加影響的.按照線性振動理論，它包含兩個方面：一是與齊次解有關的轉子振動穩定性邊界條件以及渦動頻率；二是與特解有關的質量不平衡穩態響應的振動幅值及臨界轉速.

2 穩定性邊界條件及渦動頻率

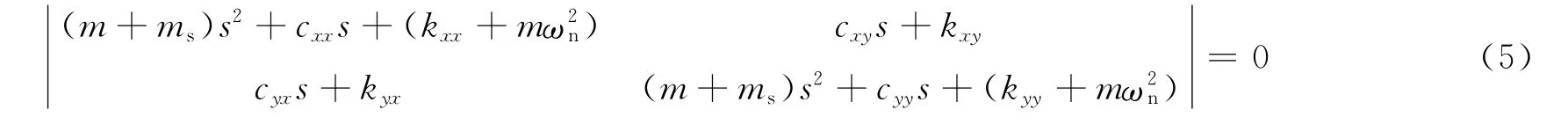
可得到復特征值s要滿足的代數方程為

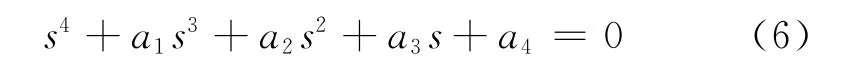
令質量比μ＝ma／m，再代入式（3）中各矩陣，有

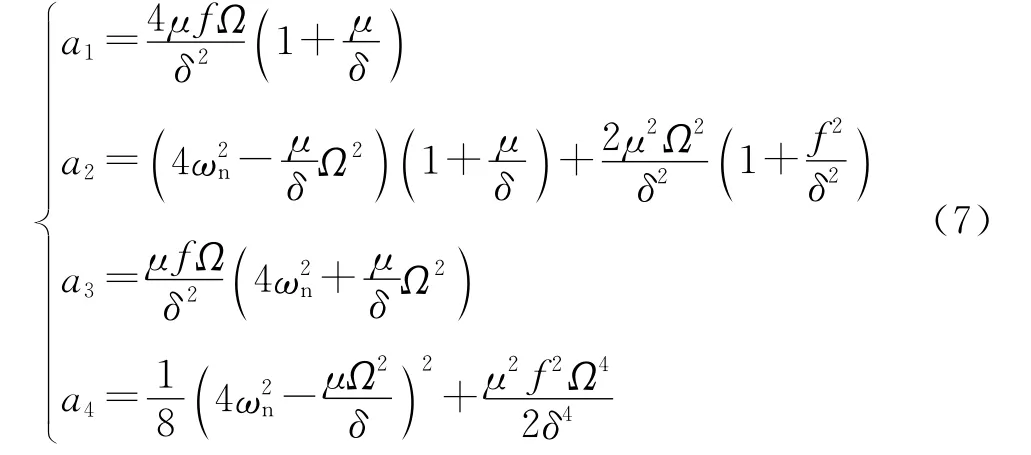
根據Hurwitz判據，使式（6）所描述的振動系統周期解處于穩定狀態的充要條件是它的系數滿足

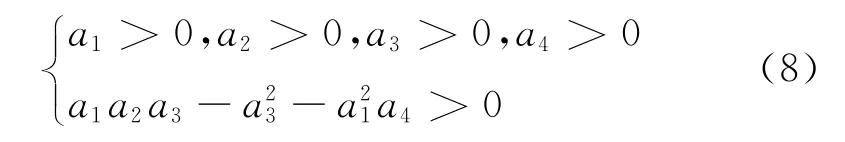
由于在式（8）中始終有a1＞0，a3＞0，a4＞0，并且對于實際核電主泵電機的結構參數，只有當間隙比δ非常大且滿足δ3－μδ2－2μf2＞0的條件時，才會出現a2≤0的情況.因此在通常情況下，若再定義Ωc為失穩轉速，可根據的要求得到判定轉子振動穩定性的邊界條件為

對于摩擦因數f＝0 的特殊情況，系數a1＝a3＝0，不能直接利用Hurwitz判據，但可通過直接求解式（6）的復特征值

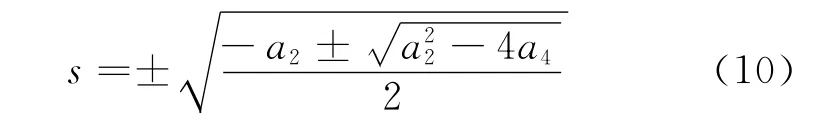
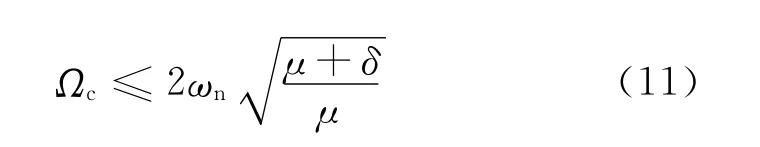
從式（9）可以看到，當摩擦因數f≠0 時，轉子振動的穩定性邊界與任何結構參數無關，只要轉子的工作轉速大于轉子固有頻率的2 倍時即出現失穩.對于摩擦因數f＝0 的特殊情況，根據式（11），轉子振動的穩定性邊界大于2倍轉子固有頻率，并與質量比μ 和間隙比δ 有關.

若令復特征值s＝σ±jω，其中σ和ω 分別為復特征值s的實部和虛部，并定義轉速比α＝Ω／ωn、阻尼比γ＝σ／ωn和頻率比αn＝ω／ωn，還可通過直接求解式（6）的復特征值，并根據其實部判定轉子振動的穩定性以及由虛部確定其渦動頻率.假定工程上摩擦因數f＝0.02，圖3給出了對于不同間隙比δ 時轉子振動穩定性邊界的變化，其中實線為第一階振動，虛線為第二階振動.由圖3可以看到，不論間隙比δ如何變化，式（9）始終成立.圖4給出了渦動頻率的計算結果，其中實線為第一階振動，虛線為第二階振動.由圖4可以看出，在較大的轉速范圍內，轉子振動的渦動頻率遠小于其固有頻率，其原因在于間隙環流中的附加質量ms.由圖4還可以看出，隨著間隙比的不同，轉子振動存在第一階渦動頻率為零的轉速，這是一種非周期不穩定狀態，也應引起重視.

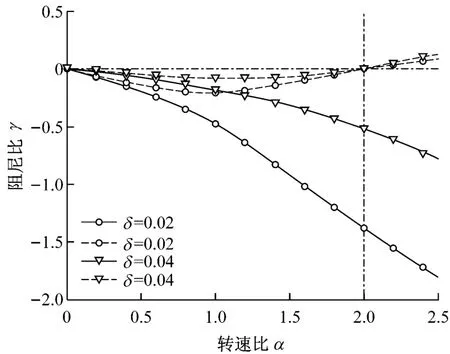
圖3 不同間隙比下的阻尼比Fig.3 Ratio of damping for different clearance ratios

圖4 不同間隙比下的頻率比Fig.4 Frequency ratio for different clearance ratios

3 質量不平衡響應的振幅及臨界轉速

任何轉子都存在不同程度的質量不平衡，若將質量不平衡的離心力在2 個坐標x、y 方向上的載荷表示為fx＝f0cosΩt及fy＝f0sinΩt，則可將有間隙環流轉子振動的質量不平衡響應表示為

展開上式并代入式（4），再令

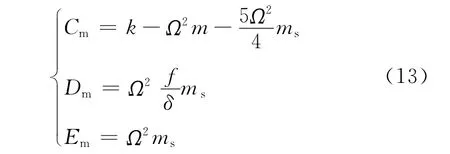
可以得到計算振動的質量不平衡響應振幅的代數方程為

式中：xc＝Xcosφx；xs＝－Xsinφx；ys＝Ycosφy；yc＝Ysinφy；tanφx＝－xs／xc；tanφy＝yc／ys.

通過代數求解式（14），并根據式（12）中振幅和相位角的定義有X＝Y＝Am及φx＝φy＝φm，若再令與系統參數有關的等效阻尼比

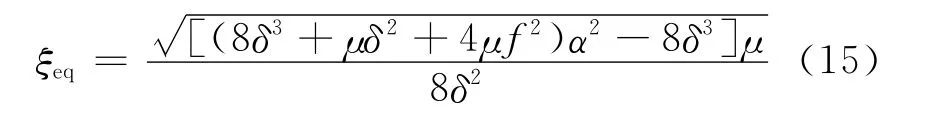
可得到振幅和初始相位

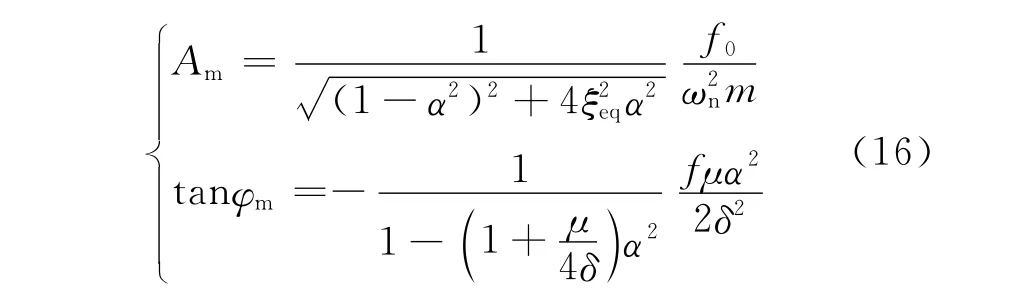
顯然，間隙環流以等效阻尼比ξeq的方式對轉子振動質量不平衡響應振幅Am產生影響，它不但與間隙環流的結構參數有關，而且還隨轉速發生變化.

可根據振幅Am的極值條件確定臨界轉速比αc，即令?Am／?α＝0，有

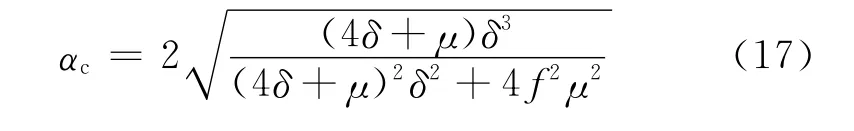
假定工程范圍的摩擦因數f＝0.02，圖5給出了等效阻尼比ξeq隨不同間隙比δ的變化.從圖5可以看出，等效阻尼比與間隙比成反比、與轉速比成正比.圖6給出了振幅比）隨不同間隙比δ的變化，同樣可由振幅比的變化看到間隙比的阻尼效應.此外，圖中虛線表示無間隙環流時的振幅比，當αc＝1時出現共振；圖中實線則不同，有間隙環流時，振幅出現極值的轉速比αc＜1，表現出臨界轉速下降，且降低程度與間隙比成反比.

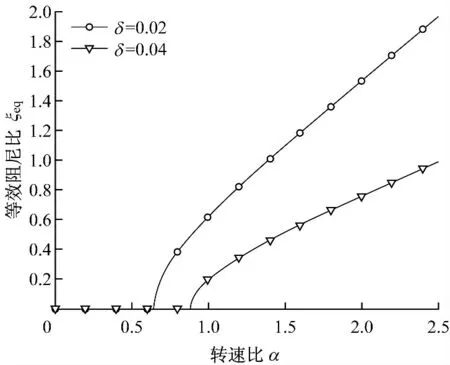
圖5 不同間隙比下的等效阻尼比Fig.5 Ratio of equivalent damping for different clearance ratios

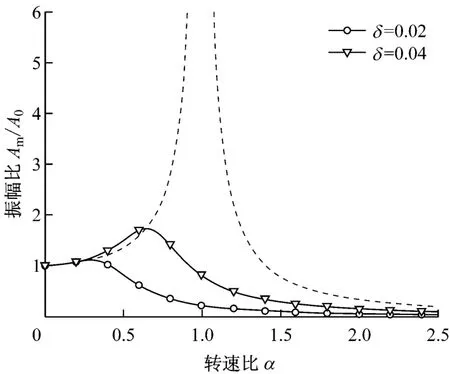
圖6 不同間隙比下的振幅比Fig.6 Amplitude ratio for different clearance ratios

值得指出的是，雖然間隙環流會降低振幅出現極值時的臨界轉速，但其阻尼效應同樣也會使轉子振幅的極值下降，通常不至于產生比較嚴重的后果.

4 屏蔽電機主泵轉子振動的有限元分析

前面討論了間隙環流對簡單轉子振動的影響，解析地給出了一些影響特征和規律.但對于實際的核電屏蔽電機主泵，由于轉子結構的復雜性以及間隙環流作用的有限區域，還需要采用有限元方法進行進一步的分析計算.

對于圖7所示的屏蔽電機主泵轉子，若令轉子振動的坐標方向為z＝｛x，y｝T，采用有限元方法建立的轉子振動微分方程可表示為

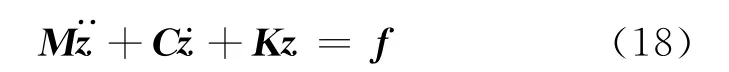
式中：M 為質量矩陣；C 為阻尼矩陣；K 為剛度矩陣；f 為作用在轉子上的質量不平衡激勵載荷.

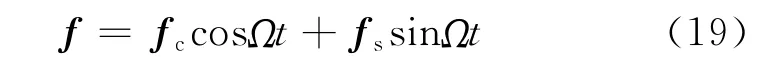
M、C、K 矩陣主要由三方面構成：一是轉子的結構參數，可利用空間梁單元［12］以等效的彎曲剛度和截面質量離散化近似；二是間隙環流的動力學特性，可利用式（3）的系數直接施加到相應的節點；三是軸承的支撐參數，為突出間隙環流的影響，只選取軸承彈簧系數.

圖7 屏蔽電機主泵轉子及有限元模型Fig.7 Finite element model for the rotor of canned motor pump

由于式（18）為非對稱矩陣系統，不能在傳統的實空間求解，需要根據復模態理論將其轉換到狀態空間

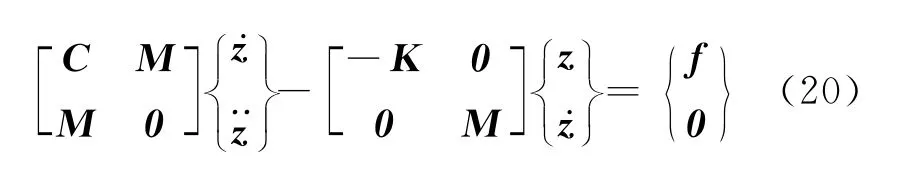
再令z（t）＝Aest并代入上式的齊次方程中，得到復特征值s＝σ±jω，最終以此判定轉子振動的穩定性及渦動頻率.若令zc＝｛xcyc｝T，zs＝｛xsys）T，可將轉子振動質量不平衡穩態相應表示為z＝zccosΩt＋zssinΩt，將其代入式（18）得到

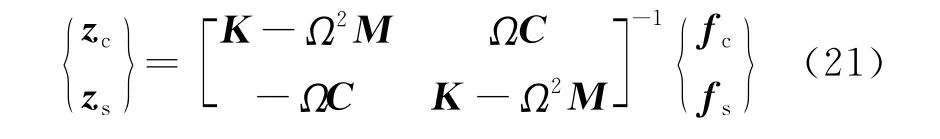
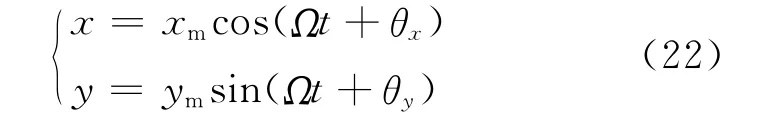
具體計算時利用Matlab軟件編制了相應的計算分析程序.圖7所示轉子振動有限元模型共分成37個節點，間隙環流作用在等效直徑為D＝0.615 m 的轉子本體12～20節點，軸承支撐在跨距為L＝3.420m 的6 和25 節 點，彈 簧 系 數 為kxx＝kyy＝1.29×109N／m，質量不平衡載荷集中作用在上下飛輪的3和35節點，并且f3＝f35＝0.223N，轉子材料彈性模量為E＝2.06×1011N／m2，定轉子與流體摩擦因數取f＝0.02，定轉子間隙比為δ＝0.02，略去了轉子結構阻尼和電磁彈性系數.

不考慮間隙環流，只有軸承支撐彈簧系數時轉子振動固有頻率的基頻為ω0＝38.98Hz，其他各階固有頻率分別為ωn1＝1.00ω0，ωn2＝1.09ω0，ωn3＝1.48ω0，ωn4＝3.56ω0，相應的振動模態示于圖8.

考慮間隙環流時，模態坐標下轉子振動的阻尼σ和頻率ω 以成對的方式隨轉速Ω 發生變化，分別對應于ωn1～ωn3的前六階計算結果示于圖9 和圖10.從圖9和圖10中可以明顯看到間隙環流對第一階固有頻率ωn1和第三階固有頻率ωn3的影響較大，而對第二階固有頻率ωn2的影響較小.這是由于只有在轉子本體處才存在間隙環流，根據圖8中的轉子振動模態，可以得出間隙環流只對轉子本體振動較大的模態產生明顯影響，它表現在轉子振動存在2種失穩現象：一是Ω＞2ωn1或者Ω＞2ωn2時，σ＞0出現周期性失穩；二是在Ω＝1.10ωn1附近存在ω＝0的非周期性失穩.比較它們與圖3 和圖4 中δ＝0.02的結果，可以看出單圓盤轉子的分析結論與有限元前兩階（對應ωn1）模態計算結果的特征與規律是一致的.

對于轉子振動質量不平衡穩態響應，圖11給出了軸承支撐處和轉子本體中部的振幅計算結果.無間隙環流時有3 個振幅極值點，分別發生在Ω＝ωn1、Ω＝ωn2和Ω＝ωn3處.有間隙環流時明顯的振幅極值點只有2個，分別為對應ωn2的Ω＝1.05ω0和對應ωn3的Ω＝1.13ω0.與ωn1相對應的極值點估計發生在Ω＝0.75ω0附近，但如圖9所示，由于此時有較大的阻尼作用，故其振幅不易辨識.

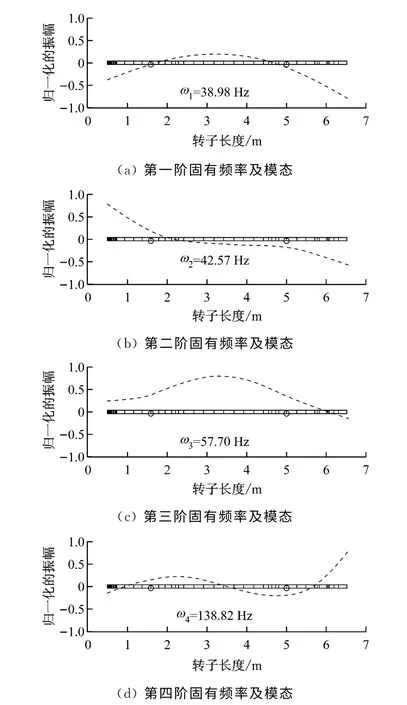
圖8 無間隙環流時轉子振動固有頻率及模態Fig.8 Natural frequency and mode of rotor vibration without annual flow

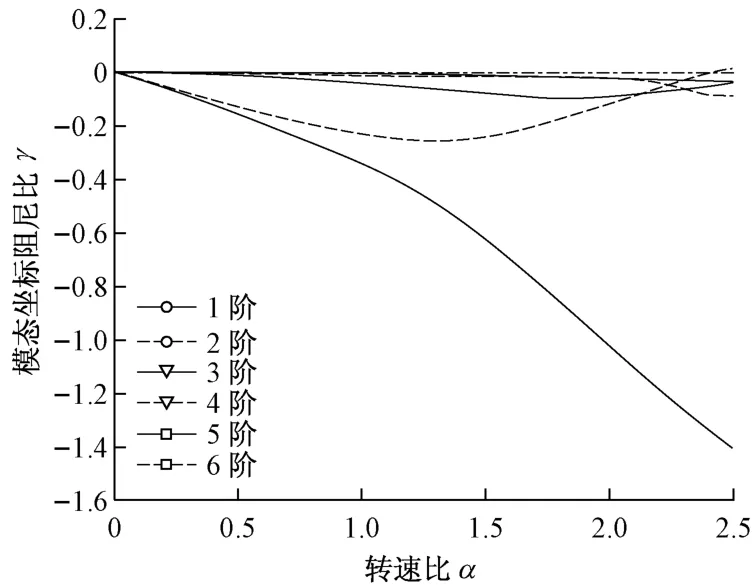
圖9 模態坐標阻尼比Fig.9 Modal damping ratio

由此可以推斷，間隙環流等效阻尼使振幅極值和臨界轉速下降的特性與轉子振動的模態密切相關，還需要進行深入研究.

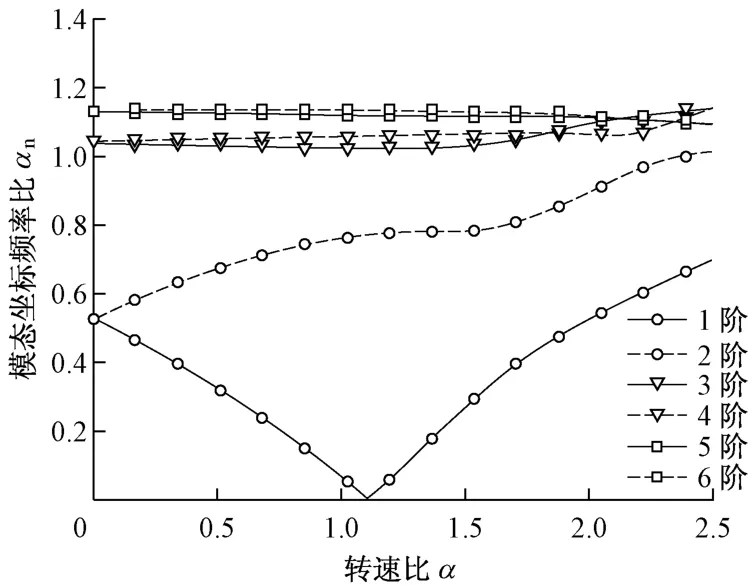
圖10 模態坐標頻率比Fig.10 Modal frequency ratio

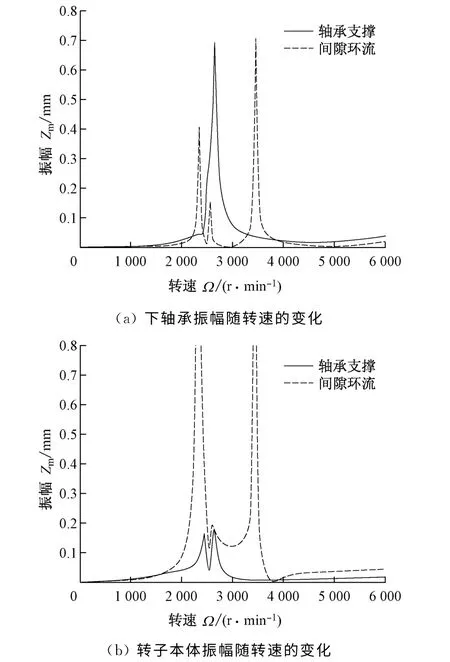
圖11 質量不平衡穩態響應振幅Fig.11 Steady state response amplitude of unbalanced rotor vibration

5 結 論

對于可簡化為單圓盤的轉子振動，間隙環流的影響表現在：

（1）當轉子工作轉速大于固有頻率的2倍時，間隙環流會使轉子振動出現周期性失穩；在工作轉速范圍的某個特定轉速，隨著間隙比的不同，間隙環流可能使轉子振動出現非周期性失穩.

（2）間隙環流會降低轉子振動的渦動頻率，主要因素是附加質量，降低程度與結構參數間隙比成反比.

（3）間隙環流使轉子振動質量不平衡穩態響應振幅下降，主要原因是等效阻尼的作用.與渦動頻率相對應的振幅出現極值的臨界轉速也同樣下降.

（4）間隙環流的主要危害是對轉子振動穩定性的影響.對于剛性轉子（工作轉速低于固有頻率）沒有任何問題，但對于柔性轉子（工作轉速高于固有頻率）則要特別小心.

上述結論同樣適用于實際的核電主泵電機轉子振動，但間隙環流的影響程度與轉子振動的各階模態密切相關.對于第一階振動模態，單圓盤轉子的分析結論與有限元計算結果是一致的，對于高階振動模態，還需要進一步研究.

［1］ ANTUNES J，AXISA F，GRUNENWALD T.Dynamics of rotors immersed in eccentric annular flow.Part 1：Theory［J］.Fluids and Structures，1996，10（8）：893－918.

［2］ FRITZ R J.The effects of an annular fluid on the vibrations of a long rotor.Part 1：theory［J］.ASME Journal of Basic Engineering，1970，92（4）：923－929.

［3］ GRUNENWALD T，AXISA F，BENNETT G，et al.Dynamics of rotors immersed in eccentric annular flow.Part 2：experiments［J］.Fluids and Structures，1996，10（8）：919－944.

［4］ FRITZ R J.The effects of liquids on the dynamic motions of immersed solids［J］.Journal of Engineering for Industry，1972，94（1）：167－173.

［5］ 成德，姚振強，薛亞波，等.間隙環流作用下的轉子動力學性能分析［J］.上海交通大學學報，2014，48（2）：271－276.CHENG De，YAO Zhenqiang，XUE Yabo，et al.Dynamic behavior of a rotating shaft immersed in a fluid annulus［J］.Journal of Shanghai Jiaotong University，2014，48（2）：271－276.

［6］ 孫啟國，虞烈.間隙環流中同心渦動轉子動特性的研究［J］.動力工程，2000，20（5）：906－910.SUN Qiguo，YU Lie.Study of dynamic characteristics for fluid machine rotor immersed in annular liquid flow［J］.Journal of Power Engineering，2000，20（5）：906－910.

［7］ 蔣慶磊，邢桂坤，吳大轉，等.離心泵內小間隙環流瞬態流體力計算［J］.浙江大學學報，2012，46（5）：929－934.JIANG Qinglei，XING Guikun，WU Dazhuan，et al.Computation of transient fluid induced force of small clearance flow in centrifugal pump［J］.Journal of Zhejiang University，2012，46（5）：929－934.

［8］ 師名林，王德忠，張繼革.Jeffcott轉子－環流耦合系統動力學建模及分析［J］.上海交通大學學報，2012，46（9）：1503－1508.SHI Minglin，WANG Dezhong，ZHANG Jige.Dynamic modeling and analysis of Jeffcott rotor－annular flow coupled system［J］.Journal of Shanghai Jiaotong University，2012，46（9）：1503－1508.

［9］ 黃文振，黃步玉，董勛.一般線性多自由度阻尼系統的廣義復模態理論［J］.上海交通大學學報，1987，21（3）：100－107.HUANG Wenzhen，HUANG Buyu，DONG Xun.General model analysis method for linear multi－degree damping system［J］.Journal of Shanghai Jiaotong University，1987，21（3）：100－107.

［10］ 鐘一鍔，何衍宗，王正，等.轉子動力學［M］.北京：清華大學出版社，1987.

［11］ TIMOSHENKO S，YOUNG D H，WEAVER W，J R.Vibration problems in engineering［M］.New York，USA：John Wiley ＆Sons，Inc.，1974.

［12］ 貽權，何福保.彈性和塑性力學中的有限單元法［M］.北京：機械工業出版社，1983.