中國造船企業(yè)的量子Stackelberg博弈與國際競爭*
楊 戟 馮衛(wèi)東 馮影影 王 霞
(1.華中科技大學文華學院數(shù)學建模實驗室 武漢 430074)(2.武漢數(shù)字工程研究所 武漢 430205)(3.武漢信息傳播職業(yè)技術(shù)學院基礎科學部 武漢 430223)
中國造船企業(yè)的量子Stackelberg博弈與國際競爭*
楊 戟1馮衛(wèi)東2馮影影3王 霞1
(1.華中科技大學文華學院數(shù)學建模實驗室 武漢 430074)(2.武漢數(shù)字工程研究所 武漢 430205)(3.武漢信息傳播職業(yè)技術(shù)學院基礎科學部 武漢 430223)
近三十年來中國船舶工業(yè)取得了巨大的成就,年造船噸位的世界排名由第十七位上升到前三位,大量先進設施的投入使用及對日韓造船技術(shù)的學習使生產(chǎn)效率大大提高。我國造船企業(yè)必須在提高核心競爭力的同時,努力收集各種“競爭情報”以便在復雜的國際造船業(yè)競爭中能做出正確的決策,提高國際競爭力。論文結(jié)合Stackelberg博弈的理論優(yōu)勢,先用經(jīng)典Stackelberg博弈模型計算出先行造船企業(yè)的“先行優(yōu)勢”,再用完全信息離散分布的量子Stackelberg博弈模型來確定各種參數(shù)對“先行優(yōu)勢”的影響,以及“競爭情報”對整個量子Stackelberg博弈的重要作用。
競爭情報;量子Stackelberg博弈;最小化量子模型
Class NumberN941
1 引言
近三十年來中國船舶工業(yè)取得了巨大的成就,年造船噸位的世界排名由第十七位上升到前三位,許多高技術(shù)船舶的設計與制造技術(shù)都已基本掌握,大量先進設施的投入使用及對日韓造船技術(shù)的學習使生產(chǎn)效率大大提高。同時,大連新船重工、外高橋造船廠等現(xiàn)代化造船企業(yè)發(fā)展勢頭良好[1]。然而,根據(jù)邁克爾·波特的鉆石體系理論[2]我國與國外先進造船國家之間仍存在著很大的差距。我國造船企業(yè)只有努力培養(yǎng)自己的核心競爭力,才能在激烈的競爭中掌握主動權(quán)[3]。在提高核心競爭力的同時,我國造船企業(yè)還要努力收集各種“競爭情報”以便在復雜的國際造船業(yè)競爭中能做出正確的決策,提高競爭力。
2 “競爭情報”的收集
競爭情報是對競爭環(huán)境、競爭形勢的全方位研究。“競爭情報”不光是對競爭信息的收集,更是對競爭對手參與的競爭市場行為的研究。“競爭情報”的收集過程就是對整個競爭環(huán)境和競爭對手的全面監(jiān)控的過程,其最終的目的就是競爭策略的選擇。競爭企業(yè)能根據(jù)自己擁有的“競爭情報”,利用博弈的思想做出最有利于自己的決策。
對于我國造船企業(yè)來說,“競爭情報”收集的工作應該包含以下階段,如表1所示。

表1 我國造船企業(yè)“競爭情報”收集工作階段
隨著“競爭情報”的收集,參與國際競爭的我國造船企業(yè)的信息結(jié)構(gòu)和決策方式也隨之改變。通過分析競爭對手和本國企業(yè)自身的情報需求、競爭環(huán)境,可以最終影響我國造船企業(yè)的競爭策略的選擇,所以“競爭情報”作為一個關鍵的變量,在整個國際造船競爭中具有十分重要的作用。
3 量子博弈理論簡介
量子博弈論是經(jīng)典博弈理論和量子理論(特別是量子信息理論)結(jié)合后形成了一門新興的交叉學科。1999年,J.Eisert等首次研究了囚徒困境的量子化模型[4]。分析表明,如果博弈雙方采用量子策略,則可以解決經(jīng)典博弈中的困境,處于最大糾纏態(tài)的量子博弈要明顯優(yōu)于經(jīng)典博弈。隨后,經(jīng)典博弈中的許多模型被量子化,得到了不同于經(jīng)典理論的奇妙結(jié)果,解決了許多經(jīng)典博弈論無法解決的問題,如囚徒困境、PQ翻硬幣問題等。除了理論研究之外,J.Du等首次用核磁共振量子計算機實現(xiàn)了囚徒困境這一量子博弈的全過程,并得到了與理論計算完全一致的結(jié)論[5]。
Stackelberg模型是博弈論中一個典型的動態(tài)博弈模型。在該模型中,產(chǎn)量決定產(chǎn)品的價格,且兩個企業(yè)按照先后順序選擇各自的策略。C.F.Lo等采用最小化量子模型研究了完全信息離散分布的量子Stackelberg博弈。分析表明,相對于經(jīng)典情況,正的量子糾纏增強先行優(yōu)勢,負的量子糾纏減弱先行優(yōu)勢。在信息離散分布的Stackelberg博弈模型中,先行企業(yè)的不確定信息將減弱的先行優(yōu)勢,但是,正的量子糾纏將增強先行企業(yè)對信息不確定度的容忍程度。
4 基于量子Stackelberg博弈理論的造船企業(yè)國際競爭模型
假設在國際造船市場上某國外企業(yè)(領頭企業(yè)1)一直致力于某型船模的設計和制造(如LNG、VLCC及好望角型散貨船)我國造船企業(yè)(尾隨企業(yè)2)經(jīng)過“競爭情報”收集與分析后決定生產(chǎn)該型船舶,于是市場競爭(博弈)就自然的發(fā)生了。
4.1 造船企業(yè)的完全信息經(jīng)典Stackelberg博弈模型
Stackelberg模型討論的是生產(chǎn)同種商品的兩家企業(yè)選擇產(chǎn)量,產(chǎn)品的價格由產(chǎn)量決定。利用該模型,領頭造船企業(yè)1首先選擇產(chǎn)量q1≥0。尾隨造船企業(yè)2經(jīng)過收集“競爭情報”觀測到q1,然后選擇自己的產(chǎn)量q2≥0。因此,這是一個完全信息動態(tài)博弈模型。這里,造船企業(yè)1和造船企業(yè)2的行動空間A1=A2=[0,+∞)是連續(xù)空間。由于造船企業(yè)2選擇行動q2依賴于q1,因此可表示為q2=A2(q1)。收益函數(shù)應為μi=μi(q1,q2)=μi(q1,A2(q1)),i=1,2。假定逆需求函數(shù)為P(Q)=a-Q=a-(q1+q2)(這里Q=q1+q2表示總產(chǎn)量),兩個企業(yè)有相同的不變單位成本c≥0。那么,造船企業(yè)1和造船企業(yè)2的利潤函數(shù)分別為給出用“逆向歸納法”找出子博弈精煉納什均衡的詳細過程。首先分析在造船企業(yè)1選擇q1的條件下,造船企業(yè)2選擇產(chǎn)量q2的最優(yōu)反應q2=R2(q1)。
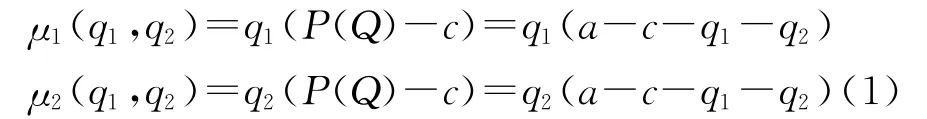
要使造船企業(yè)2的收益函數(shù)達到最優(yōu)化,即
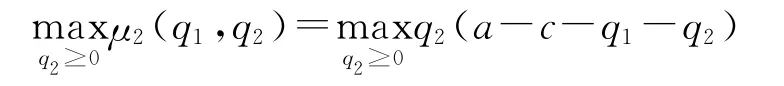
利用微積分求極值的方法,令收益函數(shù)μ2關于q2的一階導數(shù)等于0,解出最優(yōu)反應函數(shù)為
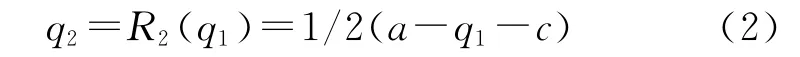
由于造船企業(yè)1知道造船企業(yè)2一定根據(jù)最優(yōu)反應q2=R2(q1)選擇產(chǎn)量q2,則在決策的第一階段,造船企業(yè)1的決策問題也就是求解最優(yōu)化問題
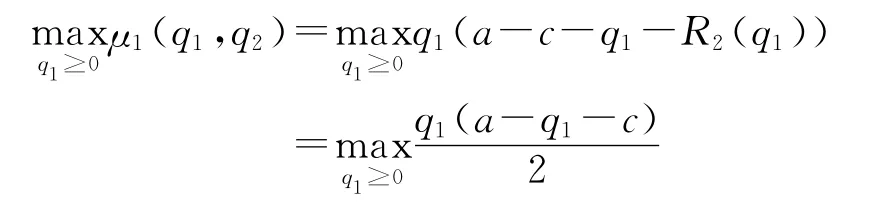
由收益函數(shù)μ1關于q1的一階導數(shù)等于0,可解得
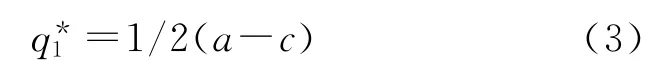
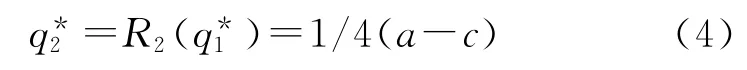
這就是該模型的子博弈精煉納什均衡結(jié)果,也稱為Stackelberg均衡結(jié)果。兩個造船企業(yè)的利潤分別為
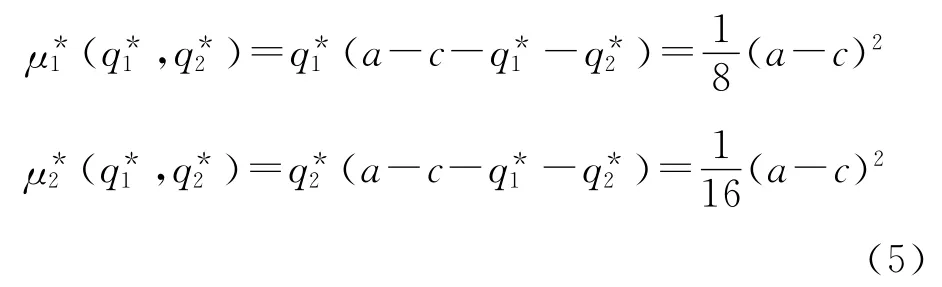
4.2 造船企業(yè)的完全信息離散分布的量子Stackelberg博弈模型
2002年,H.Li等首次建立了“最小化量子模型”[6],如圖1所示。
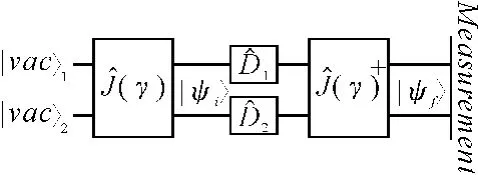
圖1 最小化量子模型
2003年,C.F.Lo等首次采用最小化量子模型研究了完全信息的量子Stackelberg博弈模型[7]。利用該模型,把兩個造船企業(yè)實際產(chǎn)量
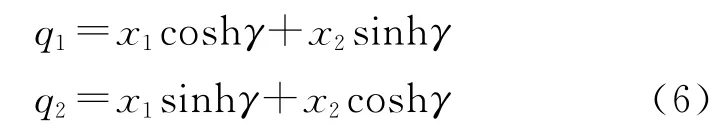
代入利潤函數(shù)表達式(1),可得兩個造船企業(yè)的利潤函數(shù)分別為
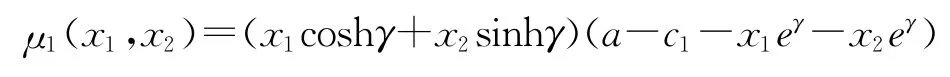
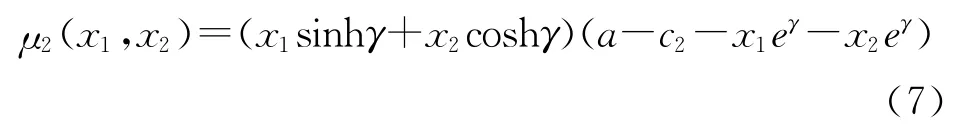
由逆向歸納法可得該量子博弈模型的最優(yōu)解:
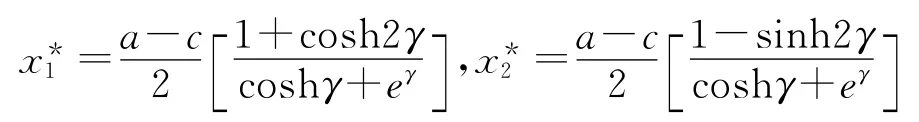
令k=a-c,計算可得各個造船企業(yè)的利潤和先行優(yōu)勢分別為
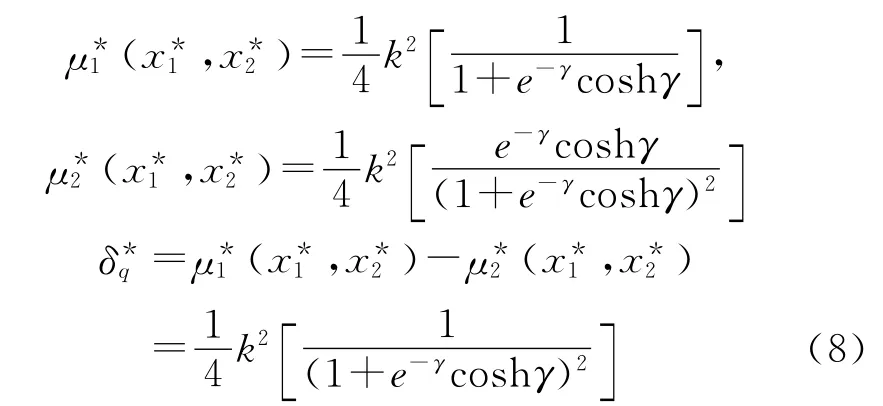
由式(8)可知,當γ≥0時,先行優(yōu)勢δ*q關于γ單調(diào)遞增;當γ<0時,先行優(yōu)勢δ*q關于γ單調(diào)遞減;當γ=0時,該模型即為經(jīng)典博弈模型。所以,相對于經(jīng)典情況,正的量子糾纏將增強先行優(yōu)勢,負的量子糾纏將減弱先行優(yōu)勢。
4.3 造船企業(yè)的不完全信息離散分布的量子Stackelberg博弈模型(競爭情報在博弈中的作用)
2005年,C.F.Lo等采用最小化量子模型研究了不完全信息離散分布的量子Stackelberg博弈模型[8]。其中,造船企業(yè)1由于沒有“競爭情報”收集不完全,所以并不知道造船企業(yè)2的產(chǎn)品成本c2,只知道c2等于高成本c2H和低成本c2L的概率分別為θ和1-θ。由海薩尼轉(zhuǎn)換,可得造船企業(yè)1和造船企業(yè)2的利潤函數(shù)分別為
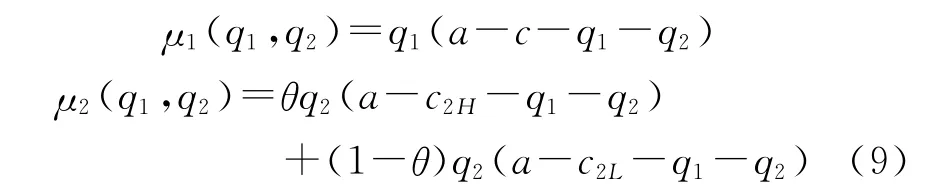
同樣的,采用最小化量子模型,并把測量結(jié)果代入利潤函數(shù)式(9),可得:

由逆向歸納法可得該量子博弈模型的最優(yōu)解,代入可得各個造船企業(yè)的利潤和先行優(yōu)勢分別為
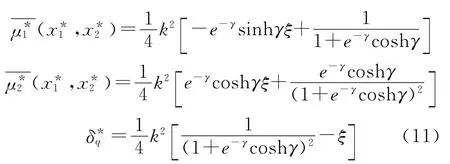
由式(11)可知,領頭造船企業(yè)要想保持先行優(yōu)勢,自變量ξ必須滿足:
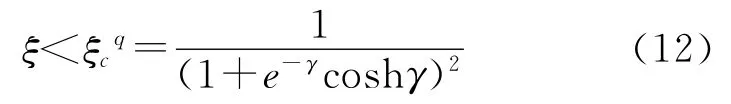
自變量ξcq表示先行造船企業(yè)在保持先行優(yōu)勢時對信息不確定度的容忍程度。ξcq關于量子糾纏度γ單調(diào)遞增,當γ=0時取得最小值1/4,當γ→∞時ξcq趨近于最大值4/9。換言之,正的量子糾纏將增強先行造船企業(yè)對信息不確定度的容忍程度。
5 結(jié)語
通過上文論述,在參與競爭的造船企業(yè)都是理性的前提下,可以得到如下結(jié)論:
1)領頭造船企業(yè)的先行優(yōu)勢是客觀存在的。由經(jīng)典Stackelberg博弈模型可知領頭造船企業(yè)的利潤大于尾隨造船企業(yè)的利潤,這是領頭造船企業(yè)首先行動(先進入市場)的結(jié)果。
2)領頭造船企業(yè)的先行優(yōu)勢不是一成不變的。由完全信息離散分布的量子Stackelberg博弈模型知道,正的量子糾纏將增強領頭造船企業(yè)的先行優(yōu)勢,負的量子糾纏將減弱先行優(yōu)勢。
3)打破領頭造船企業(yè)的先行優(yōu)勢的關鍵就是努力收集競爭對手的“競爭情報”并保護自己的“信息”不被競爭對手知道。由不完全信息離散分布的量子Stackelberg博弈模型可以看到,領頭造船企業(yè)的先行優(yōu)勢關于“信息的不確定度”單調(diào)遞減,即領頭造船企業(yè)對信息的不確定將會減弱它的先行優(yōu)勢。
4)如果我國造船企業(yè)變成“領頭企業(yè)”,該如何保住先行優(yōu)勢。努力收集競爭對手的“競爭情報”并保護自己的“信息”不被競爭對手知道是保住先行優(yōu)勢的關鍵。若用ξcq表示先行造船企業(yè)在保持先行優(yōu)勢時對信息不確定度的容忍程度。ξcq關于量子糾纏度γ單調(diào)遞增,當γ=0時取得最小值1/4,當γ→∞時ξcq趨近于最大值4/9。換言之,正的量子糾纏將增強先行造船企業(yè)對信息不確定度的容忍程度。
5)市場的競爭就是“情報”的競爭、“信息”的競爭。無論是領頭企業(yè)還是尾隨企業(yè)為了獲取最大的利益,都應該把收集“競爭情報”放在重要的地位。
[1]長塚誠治.中國造船技術(shù)的實力[J].海外海事情報,2002(8):1-5.
[2]邁克爾 波特.國家競爭優(yōu)勢[M].北京:華夏出版社,2003.
[3]陳強.論中國造船企業(yè)的核心競爭力[J].中國造船,2004,45(1):1-6.
[4]J.Eisert,M.Wilkens.Quantum games[J].J.Modern Opt.,2000,47:2543.
[5]R.Raussendorf,D.E.Browne,H.J.Briegel.Measurement-based quantum computation with cluster states[J].Phys.Rev.A,2003,68:022312.
[6]H.Li,J.F.Du,S.Massar.Continuous-variable quantum games[J].Phys.Lett.A,2002,306:73.
[7]C.F.Lo,D.Kiang.Quantum Stackelberg duopoly[J].Phys.Lett.A,2003,318:333.
[8]C.F.Lo,D.Kiang.Quantum Stackelberg duopoly with incomplete information[J].Phys.Lett.A,2005,346:65.
China ShipbuildingEnterprises Quantum StackelbergDuopolyand the International Competition
YANG Ji1FENG Weidong2FENG Yingying3WANG Xia1
(1.Mathematical Modeling Lab,Huazhong University of Science and Technology Wenhua College,Wuhan 430074)(2.Wuhan Digital Engineering Institute,Wuhan 430205)(3.Wuhan Vocational College of Communications and Publishing,Wuhan 430223)
Over the past three decades,China's shipbuilding industry has made great achievements.The world ranking of anuual shipbuilding tonnage has risen to the top three from the previous seventeenth,numerous advanced facilities has been put into use,learning shipbuilding technology from Japanese and Korean has greatly improved the production efficiency.So,the strtegic objectives of China's shipbuilding enterprises,we struggle to achieve over the next decade,lie in keeping our status as the shipbuilding power in the world and moving realistically from shipbuilding country towards shipbuilding power.At the same time of improving core competitiveness,China's shipbuilding enterprises must strive to collect various"Competitive intelligence",so as to make the right decisions in the complex international shipbuilding situation,and to improve international competitiveness as well.Combining the theoretical advantages of Stackelberg game,this article firstly calculates out the"first advantage"of the first shipbuilding enterprises with classic model of Stackelberg game,then with the quantum Stackelberg game model of complete information descrete distributions,the influence of various parameters on the"first advantage",as well as the important role of"competitive intelligence"in the whole Stackerberg game can be defined.
competitive intelligence,quantum stackelberg duopoly,minimize quantum model
N941DOI:10.3969/j.issn.1672-9730.2015.11.003
2015年5月8日,
2015年6月25日
楊戟,男,碩士,講師,研究方向:量子運籌學、數(shù)量情報與數(shù)學模型。

