基于多步長最大信息熵的空間目標(biāo)質(zhì)心定位*
郭曉軍 徐 健 馬新星,3 劉 峰
(1.海軍航空工程學(xué)院控制工程系 煙臺 264001)(2.海軍航空工程學(xué)院研究生管理大隊(duì) 煙臺 264001)(3.海軍航空工程學(xué)院接改裝大隊(duì) 煙臺 264001)
基于多步長最大信息熵的空間目標(biāo)質(zhì)心定位*
郭曉軍1徐 健2馬新星2,3劉 峰2
(1.海軍航空工程學(xué)院控制工程系 煙臺 264001)(2.海軍航空工程學(xué)院研究生管理大隊(duì) 煙臺 264001)(3.海軍航空工程學(xué)院接改裝大隊(duì) 煙臺 264001)
高精度星敏感器星點(diǎn)光斑的質(zhì)心定位精度是星敏感器整體定位精度的基礎(chǔ),是天文導(dǎo)航、星圖識別、軌道精確定位等技術(shù)的基礎(chǔ),常需要達(dá)到角秒級和亞像素的標(biāo)準(zhǔn)。論文分析了影響定位精度的主要因素,并研究了CCD觀測圖像亞像素的高精度質(zhì)心定位方法,并分析了恒星成像時(shí)能量的分布,提出基于多步長最大信息熵的質(zhì)心定位方法,該方法使用線性疊加縮小質(zhì)心區(qū)域,利用恒星能量分布的對稱性,求取信息熵最大時(shí)的質(zhì)心位置,并采用模擬星圖驗(yàn)證比較。實(shí)驗(yàn)表明,該方法定位精度可達(dá)0.01pixel,對低信噪比條件下的質(zhì)心計(jì)算具有較好的效果。
多步長;信息熵;亞像素;質(zhì)心定位
Class NumberTP393
1 引言
在對未知目標(biāo)坐標(biāo)的星點(diǎn)成像時(shí),空間目標(biāo)觀測系統(tǒng)將恒星目標(biāo)看作是理想的點(diǎn)光源,通過離焦光學(xué)系統(tǒng)來實(shí)現(xiàn)星點(diǎn)目標(biāo)的彌散成像,通常成像系統(tǒng)在CCD平面上只占幾個(gè)像素的大小,目前最精確度的星敏感器定位精度可達(dá)0.001像素[1]。而星敏感器星點(diǎn)光斑的質(zhì)心精度是星敏感器整體精度的基礎(chǔ),它直接影響姿態(tài)角測量精度、光軸指向精度和軌道定位精度[2]。
亞像素級的質(zhì)心定位技術(shù)按處理手段不同可劃分為插值技術(shù)和擬合技術(shù)兩類。插值技術(shù)易于實(shí)現(xiàn),但對峰值兩側(cè)弱信號依賴性較強(qiáng),并且抗噪聲干擾能力弱;擬合法通過多次迭代來完成,精度較高但耗時(shí)較長。傳統(tǒng)的方法有一階矩法[3~4],質(zhì)心法、改進(jìn)的質(zhì)心法、曲面擬合法和基于邊緣的圓擬合[5~7]、Hough變換等方法。文獻(xiàn)[8]利用彌散斑的能量累加自適應(yīng)確定目標(biāo)位置,再利用平方加權(quán)的方法精確定位質(zhì)心,但針對較小目標(biāo)的情況適用性不強(qiáng)。文獻(xiàn)[9]首先通過插值法降低采樣點(diǎn)光線照度不一致的問題,再利用能量累加和平方加權(quán)的質(zhì)心定位方法,有效地降低了噪聲的干擾。文獻(xiàn)[10]在傳統(tǒng)的質(zhì)心定位方法上采用二元線性插值和自適應(yīng)窗相結(jié)合的方法,改善信噪比自動(dòng)提取目標(biāo)質(zhì)心,但在算法效率上計(jì)算量過大。基于此,本文在分析恒星能量分布的基礎(chǔ)上,提出了具有抗噪聲干擾能力和計(jì)算量較小的基于多步長信息熵的質(zhì)心定位方法。
2 質(zhì)心定位精度誤差分析
空間目標(biāo)圖像的像點(diǎn)灰度分布符合高斯型點(diǎn)擴(kuò)散函數(shù)模型,如式(1)所示:
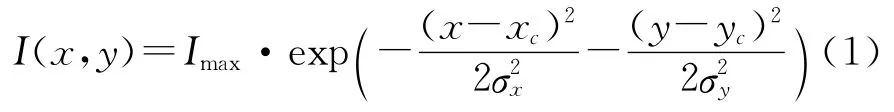
其中,x,y為星點(diǎn)坐標(biāo)位置,σx,σy為高斯彌散半徑,xc,yc為星像橫、縱坐標(biāo)質(zhì)心,Imax為最大灰度值。
星點(diǎn)圖像的質(zhì)心可以通過灰度函數(shù)的平衡點(diǎn)來計(jì)算,由圖像的一階矩和零階矩的比值來確定,如式(2)所示:
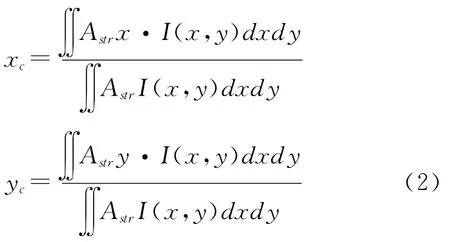
其中Astr為目標(biāo)星像區(qū)域,x、y為星像的坐標(biāo)值,I(x,y)為星像灰度函數(shù),表示CCD表面光強(qiáng)照度分布。由于采樣后得到的圖像是離散的,采樣值和感應(yīng)區(qū)的光線照度的積分成比例,由此式(2)可簡化為
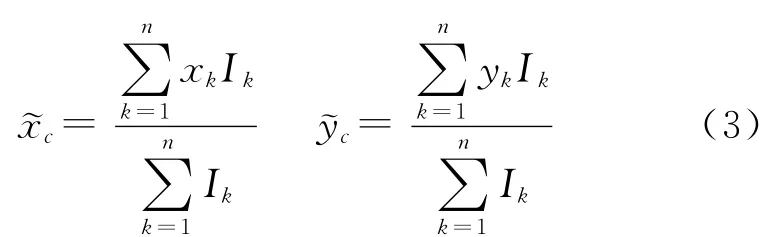
其中~xc、~yc為星圖質(zhì)心坐標(biāo),xk、yk為第k個(gè)像元的中心坐標(biāo),Ik為其對應(yīng)的灰度函數(shù)的采樣值。由于圖像采樣的近似,對星點(diǎn)質(zhì)心的定位帶來了誤差,同時(shí)由于CCD相機(jī)的讀出噪聲、暗電流等影響,將對待檢測目標(biāo)圖像的灰度值產(chǎn)生不確定性的影響,記為σn。假設(shè)x方向和y方向效果相同,僅以x方向進(jìn)行分析,如式(4)所示
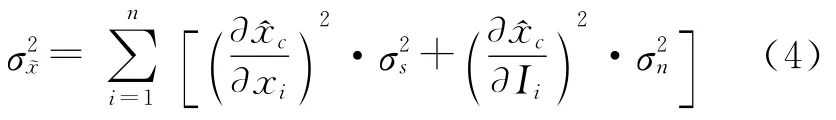
其中σ~x表示~xc的不確定性,σn表示由于噪聲引入的不確定性。引入?yún)?shù)Iw和SNR,記為
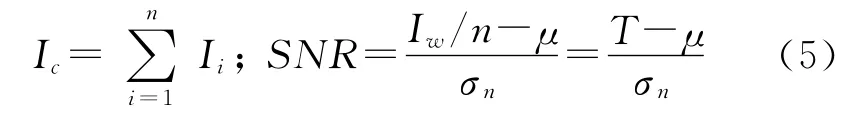
將式(5)帶入式(4)化簡后得到
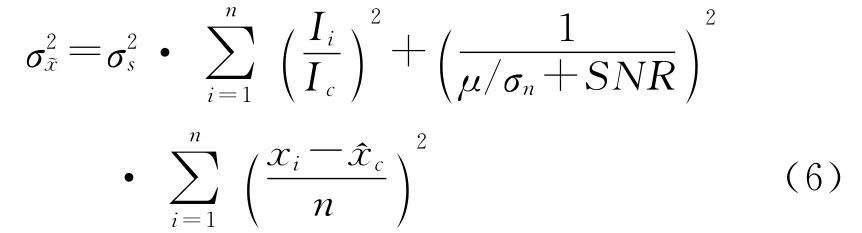
由以上分析可以看出,質(zhì)心算法的誤差主要由系統(tǒng)誤差和隨機(jī)誤差[11]決定。系統(tǒng)誤差是由在成像時(shí)像元代替灰度函數(shù)的平衡點(diǎn)引起的,可采用多步長分析,使計(jì)算結(jié)果更加接近灰度函數(shù)的平衡點(diǎn)來定位目標(biāo)質(zhì)心。隨機(jī)誤差是由讀出噪聲、暗電流噪聲等引起的,可通過信息熵理論,選取合適的閾值,達(dá)到減小背景噪聲,提高信噪比的目的。
3 基于最大信息熵的亞像素質(zhì)心定位
本文提出了基于最大信息熵理論的星像質(zhì)心定位方法,最大信息熵理論的基本思想是:從信息熵的角度分析,設(shè)定距離質(zhì)心越近的像素,熵值越大,在目標(biāo)邊緣像素,熵值較小[12]。利用CCD相機(jī)進(jìn)行成像,所得圖像的像素灰度值與物體的能量成比例關(guān)系。在確定恒星質(zhì)心時(shí),可以先假設(shè)某一點(diǎn)(x,y)是質(zhì)心點(diǎn),若該點(diǎn)不是質(zhì)心位置,則關(guān)于這一點(diǎn)的信息熵達(dá)不到最大值,在某一方向上(方便起見,常選取橫向或縱向)會(huì)存在一定的能量差值,可通過對比該方向的多步長[13](以降低噪聲的干擾)的信息熵值,來判定該點(diǎn)是不是質(zhì)心位置,在星像坐標(biāo)范圍內(nèi)信息熵達(dá)到最大值時(shí),即可定位質(zhì)心位置。信息熵定義如下所示:

其中,Px,y為二維圖像上點(diǎn)(x,y)的概率,PA和PB分別為圖像中屬于A區(qū)和B區(qū)的概率,則它們的信息熵分別為
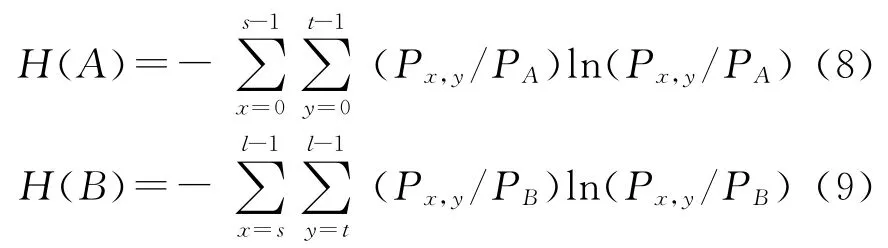
則目標(biāo)的最大二維信息熵可定義為
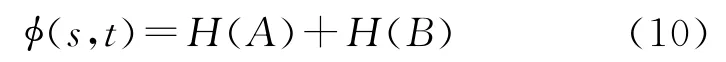
如圖1所示,圖1(a)為一張?jiān)夹菆D,圖1(b)為其灰度分布,圖2為目標(biāo)星像點(diǎn)的圖像和灰度分布。
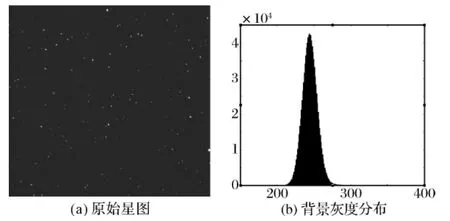
圖1 完整星空圖像及灰度分布
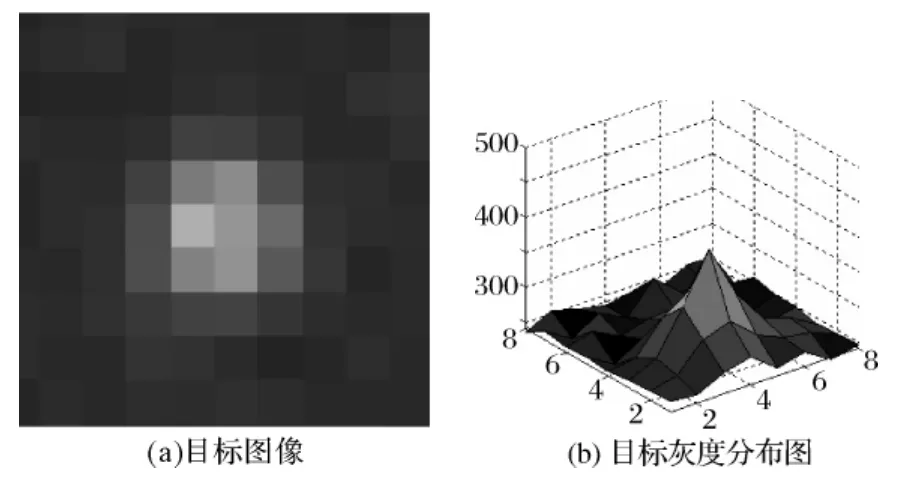
圖2 恒星和目標(biāo)成像灰度分布
理想的光學(xué)系統(tǒng)條件下,恒星成像點(diǎn)小于一個(gè)像元,無法通過算法準(zhǔn)確定位到亞像素級質(zhì)心位置,但是由于諸多因素如光學(xué)相差、大氣傳輸?shù)扔绊懀阈浅上褚话闶且粋€(gè)彌散斑[14],該彌散斑灰度分布服從高斯分布,基于此,對模擬生成星圖進(jìn)行線性插值。在計(jì)算質(zhì)心的過程中,可先確定出質(zhì)心區(qū)域,進(jìn)一步減少計(jì)算量;然后在質(zhì)心區(qū)域進(jìn)行能量差值計(jì)算,找出最小差值時(shí)的質(zhì)心位置。具體步驟如下:
第一步:質(zhì)心區(qū)域的確定。對生成的星圖,先每一列像素值相加,取出最大的1列,然后再每一行像素值相加,取出最大的1行,以像素值最大列和最大行的交點(diǎn)像元作為中心,形成一個(gè)3*3大小區(qū)域,以該區(qū)域?yàn)楹诵膮^(qū)域,在核心區(qū)域內(nèi)進(jìn)行亞像素的構(gòu)造,這樣可減小計(jì)算量,加快確定亞像素質(zhì)心位置的速度。
第二步:亞像素質(zhì)心定位。通過在核心區(qū)域內(nèi)進(jìn)行多步長最小能量差計(jì)算質(zhì)心提取。要進(jìn)行亞像素級的質(zhì)心位置確定,首先將圖像中的每一個(gè)像素點(diǎn)人為地放大,假設(shè)所有的像素點(diǎn)占有一定的平面面積,然后根據(jù)實(shí)際定位精度需求,將放大后的像素點(diǎn)進(jìn)行細(xì)分,即每一個(gè)點(diǎn)可看作由若干個(gè)更小的點(diǎn)均勻組成,文中根據(jù)定位精度和實(shí)際情況,將每個(gè)點(diǎn)均勻分成四個(gè)更小的點(diǎn)[7],插值后(m,n)處的灰度值f(m,n)計(jì)算如下[5]:
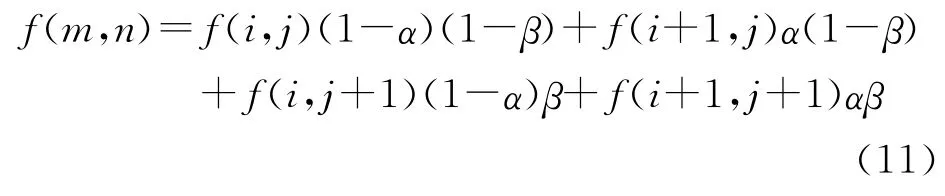
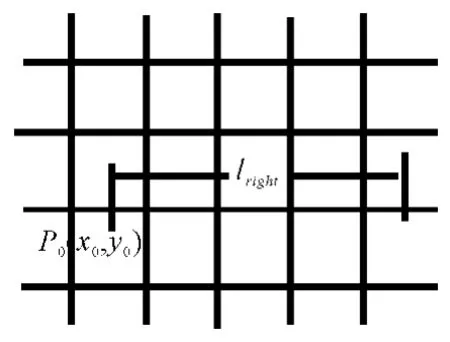
圖3 多步長灰度和示意圖
4 仿真實(shí)驗(yàn)及結(jié)果分析
對本文算法進(jìn)行驗(yàn)證,利用Matlab進(jìn)行仿真實(shí)驗(yàn),采用隨機(jī)生成的方式模擬星點(diǎn),仿真數(shù)據(jù)星像大小為[15,15]像元,采用高斯分布生成仿真圖像,圖像中噪聲采用高斯白噪聲,如圖4所示。
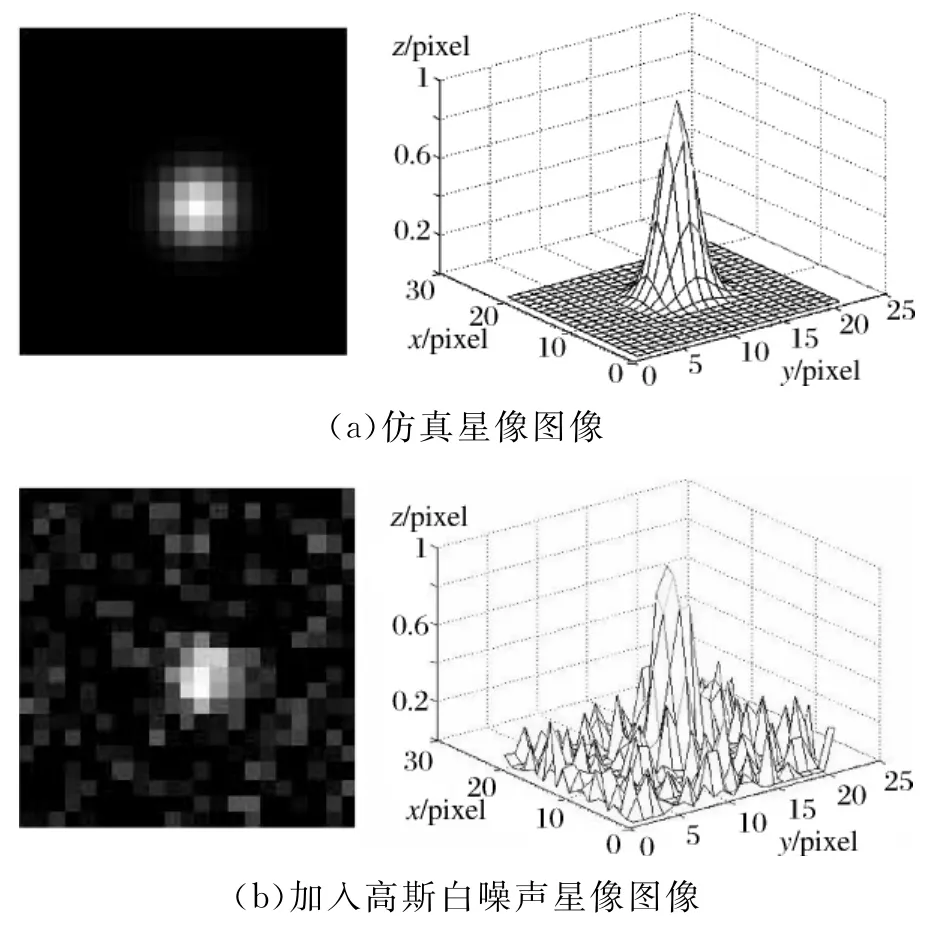
圖4 仿真結(jié)果
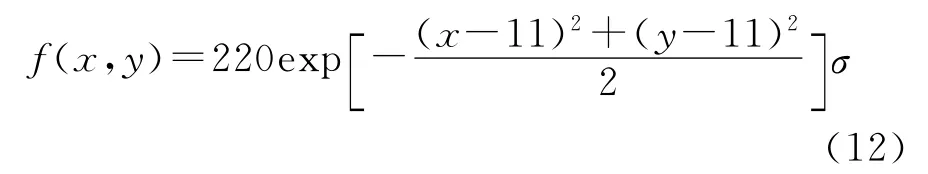
利用高斯函數(shù)可知質(zhì)心位置為(7,5),彌散半徑σ=10。以隨機(jī)模式和固定點(diǎn)模式驗(yàn)證算法誤差。
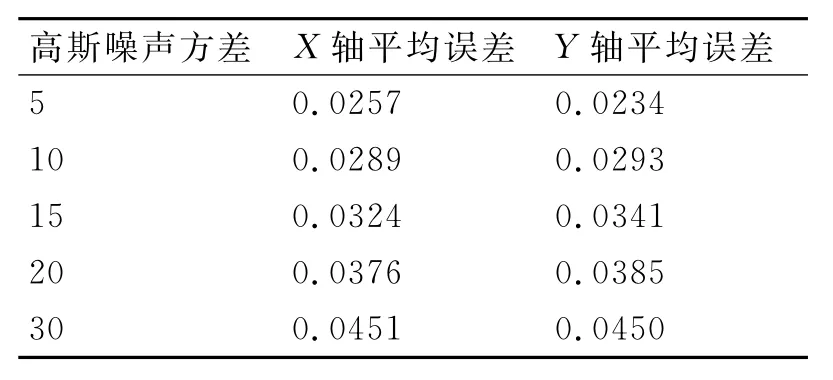
表1 隨機(jī)模式下算法誤差統(tǒng)計(jì)
對算法進(jìn)行進(jìn)一步驗(yàn)證,在固定位置(11,11)生成星點(diǎn),其他參數(shù)不變,針對不同高斯噪聲對算法進(jìn)行驗(yàn)證,采用一階矩質(zhì)心定位法、平方加權(quán)質(zhì)心定位法、高斯曲面擬合法及基于多步長最小能量差方法分別計(jì)算定位精度,采用100次定位誤差的均值作為該算法的估計(jì)誤差,結(jié)果如表2所示。從中可以看出,高斯擬合在高信噪比情況下精度最高,而本文的算法較適合低信噪比條件下的質(zhì)心定位。
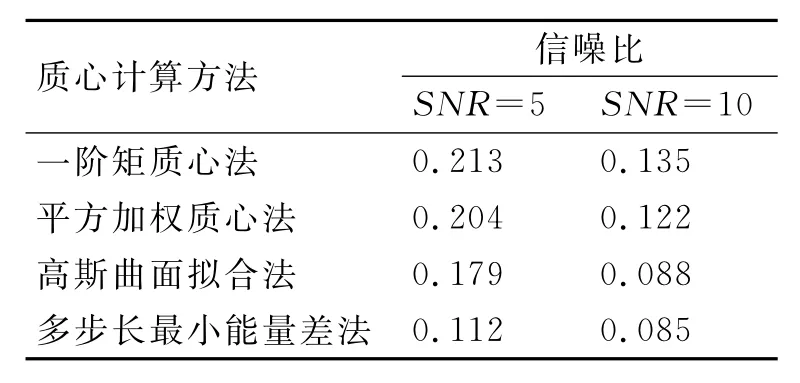
表2 不同信噪比條件下定位精度比較
圖5為使用近紅外小口徑相機(jī),早上6點(diǎn)45分拍攝的北極星2等星圖像連續(xù)15幀疊加以后的圖像,設(shè)備位于固定觀測點(diǎn)。可以看出,即使疊加星圖在一定程度上增大了信噪比,星圖的信噪比仍然很低(SNR=2.15),目標(biāo)區(qū)域邊緣與背景界限不很明顯,圖像大小為340×340像元。根據(jù)成像設(shè)備的大地坐標(biāo)和探測時(shí)刻的光軸指向(方位0°,俯仰43°),并考慮到設(shè)備測角系統(tǒng)誤差,通過計(jì)算得到的該2等北極星位于圖像中(191.287,183.943)點(diǎn)處(沒有去除設(shè)備測角誤差),使用本文算法計(jì)算恒星質(zhì)心位置為(191.712,183.725)。圖6為提取質(zhì)心位置后的星圖,虛線十字絲交點(diǎn)為理論質(zhì)心點(diǎn)位置,實(shí)線十字絲交點(diǎn)為本文算法結(jié)果。

圖5 連續(xù)15幀疊加近紅外星圖

圖6 提取質(zhì)心位置后的星圖
5 結(jié)語
恒星質(zhì)心的定位精度直接影響到天文導(dǎo)航星的匹配和定位精度,在天文導(dǎo)航中起著至為重要的作用。分析了恒星成像時(shí)的能量分布,利用高斯分布的特性,采用線性插值方式提高定位質(zhì)心的精度,提出基于分布特點(diǎn)的多步長最大信息熵恒星質(zhì)心定位方法,通過仿真實(shí)驗(yàn)和實(shí)際拍攝星圖驗(yàn)證該方法的有效性。并且該方法具有較強(qiáng)的抗干擾能力和穩(wěn)定性,平均定位精度可達(dá)到0.01像素,適用于低信噪比條件下的質(zhì)心定位計(jì)算。
[1]Kurt L Dietz,Brian D Ramsey,Cheryl D Alexander,et al.Daytime aspect camera for balloon altitudes[J].Opt Eng,2002,41(10):2641-2651.
[2]李玉峰,郝志航.星點(diǎn)圖像超精度亞像元細(xì)分定位算法的研究[J].光學(xué)技術(shù),2005,31(5):666-670.
[3]孫瑾秋,周軍,張臻,等.基于能量累加的空間目標(biāo)星相質(zhì)心定位[J].光學(xué)精密工程,2011,19(12):3043-3048.
[4]胡曉東,胡強(qiáng),雷興,等.一種用于白天星敏感器的星點(diǎn)質(zhì)心提取方法[J].中國慣性技術(shù)學(xué)報(bào),2014,22(4):481-486.
[5]白俊奇,趙春光,王壽峰,等.紅外圖像中的自適應(yīng)維納濾波噪聲抑制技術(shù)[J].光電工程,2011,11(8):79-85.
[6]劉太陽,王仕成,劉志國.多步變權(quán)重復(fù)合的通用星點(diǎn)聚心[J].光學(xué)精密工程,2011,19(10):2494-2499.
[7]Zhu X,Wu F,Xu Q.A fast star image extraction algorithm for autonomous star sensors[C]//Photonics A-sia.International Society for Optics and Photonics,2012:855821-855821-9.
[8]張春華.星空背景圖像弱小目標(biāo)運(yùn)動(dòng)檢測技術(shù)研究[D].煙臺:海軍航空工程學(xué)院博士論文,2009.
[9]Pham M D,Low K S,Chen S.An Autonomous Star Recognition Algorithm with Optimized Database[J].Aerospace and Electronic Systems,IEEE Transactions on,2013,49(3):1467-1475.
[10]魏偉,劉恩海.紅外星圖預(yù)處理及星點(diǎn)定位精度分析[J].紅外與激光工程,2014,43(3):991-996.
[11]張廣軍.星圖識別[M].北京:國防工業(yè)出版社,2011:125-129.
[12]Sun R Y,Zhao C Y.A new source extraction algorithm for optical space debris observation[J].Res Astron Astrophys,2013,13(5):604-614.
[13]萬明,張鳳鳴,胡雙.基于多步長梯度特征的紅外弱小目標(biāo)檢測算法[J].光學(xué)學(xué)報(bào),2011,10(31):1-6.
[14]王進(jìn),張輝,林玲,等.基于星敏感器的衛(wèi)星對地定姿誤差分析[J].計(jì)算機(jī)仿真,2012,29(8):68-71.
Centroid Location for Space Targets Based on Multi-step Information Entropy Energy Difference Method
GUO Xiaojun1XU Jian2MA Xinxing2,3LIU Feng2
(1.Control Engineering,Naval Aeronautical and Astronautical University,Yantai 264001)(2.Postgraduate Training Brigade,Naval Aeronautical and Astronautical University,Yantai 264001)(3.Group of Accept Equipment,Naval Aeronautical and Astronautical University,Yantai 264001)
The centroid accuracy of star tracker is the base of other accuracies.It's the base of celestial navigation,star map identification,orbit positioning and so on,which is required to reach arc second scale.This paper analyses the main factors affecting the positioning accuracy of target centroid and the method for star target centroids based on multi-step maximum information entropy is proposed.This method uses the linear superposition to narrow the centroid area,using the symmetry of the stellar energy distribution to get the difference at centroid position and obtain the centroid,then the validation comparison of simulated star images.Experiments show that the positioning accuracy of the method up to 0.01pixel,has good effect to calculate the centroid of low SNR conditions.
multi-step,information entropy,sub-pixel,centroid calculation
TP393DOI:10.3969/j.issn.1672-9730.2015.11.013
2015年5月4日,
2015年6月17日
郭曉軍,男,副教授,碩士生導(dǎo)師,研究方向:控制工程,計(jì)算機(jī)應(yīng)用。徐健,男,博士研究生,研究方向:圖像處理,模式識別。

