一種適用于突發通信的載波頻偏估計算法＊

王 林 許宏泉

（1.92493部隊2分隊 葫蘆島 125000）（2.海軍駐武漢709所軍事代表室 武漢 430205）

一種適用于突發通信的載波頻偏估計算法＊

王 林1許宏泉2

（1.92493部隊2分隊 葫蘆島 125000）（2.海軍駐武漢709所軍事代表室 武漢 430205）

論文提出了一種適用于突發通信條件下的新型載波頻偏估計算法，算法同時利用了導頻符號和數據符號。仿真結果表明，新算法的頻偏估計范圍達到了符號速率的±0.5，信噪比門限很低，而且估計的均方誤差接近克拉美－勞下界（CRLB）。新算法的運算復雜度低，非常適合于實際應用場景。

突發通信；載波同步；頻偏估計；克勞美－勞下界

Class NumberTN914.52

1 引言

在軍事通信中，為了防止被竊聽、破譯、偵收和干擾，常常使用突發通信手段，即將信息以高速率數據隨機突發的方式發送出去。由于信號在傳輸過程中暴露的時間很短，大大降低了其被截獲的概率。載波頻率偏移（以下簡稱“頻偏”）是由發射機和接收機的相對運動而產生的，對于突發通信來說，接收機必須準確、快速地估計和補償頻偏，以便正確接收數據。

目前，近香農極限的信道編碼被廣泛使用，接收機需要工作在極低信噪比下［1］。在這種情況下，通常使用導頻符號輔助調制技術，即在突發幀中插入一定數量的導頻符號，幫助接收機進行同步。

載波頻偏估計算法在許多論文中已有研究，常見的頻偏估計算法有兩類，一類是基于FFT［2］，另一類則基于相位差分［3～7］。基于FFT的算法具有很低的信噪比門限、接近CRLB的性能，但運算復雜度太高，并不是很實用。基于相位差分的算法包括Kay算法［3］、L＆R算法［4］、Fitz算法［5］、Bian算法［6］、M＆M算法［7］等。Kay算法是一種簡單的無偏估計算法，在高信噪比時性能可達到CRLB。L＆R算法、Fitz算法、Bian算法都比FFT容易實現，在中等信噪比時性能可達到CRLB，但估計范圍較小。M＆M算法性能更好，雖然運算復雜度稍高，但具有大的估計范圍。在這些算法中，M＆M算法的性能最佳，后文中將重點以它作為比較對象。

現有的頻偏估計算法，或者運算復雜度高，或者信噪比門限高，而且大部分只用到了導頻符號，而大量數據符號的相位信息則完全沒有利用到。本文將提出一種新的載波頻偏估計算法，它基于最大似然原理并進行了改進，具有信噪比門限低、估計范圍大的優點。

2 算法描述

在突發通信中，載波同步過程需要借助導頻符號。以BPSK調制的情形來分析，采用加性高斯白噪聲（AWGN）信道模型。對于一個長度為N的突發幀，第k個接收符號為

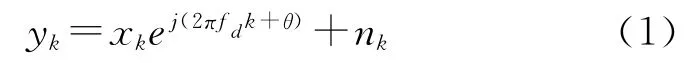
其中k滿足1≤k≤N，xk∈｛－1，1｝表示傳輸的BPSK符號，fd是按照符號速率歸一化的載波頻偏，θ是均勻分布于（－π，π］內的載波初相位。nk是獨立同分布的復高斯隨機變量，其均值為0，實部和虛部的方差分別等于N0／2。

設每幀有Np個導頻符號，全部導頻符號的下標組成集合KP。對于已知的導頻符號，接收機通過對接收信號乘以復共軛將其能量歸一化，如下式所示：

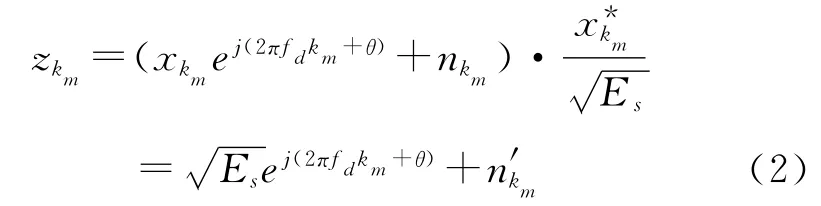
其中Es表示導頻符號的能量（所有導頻符號都具有相同的能量），且km∈KP。注意n′k與nk的統計特性一致，信噪比定義為Es／N0。對于數據符號來說，也需要如式（2）一樣乘以使得數據符號的能量也歸一化。

為了分析算法性能，引入理論估計的下界是很有必要的。CRLB是最常用的一種下界，現將頻偏估計的CRLB定義為CRLBf，表達式為［8］

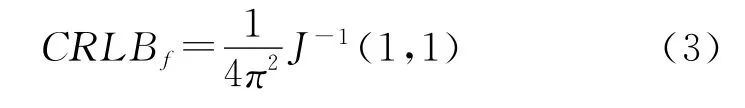
其中J為Fisher矩陣。

傳統的頻偏估計算法只利用導頻符號（而不利用數據符號），Fisher矩陣為

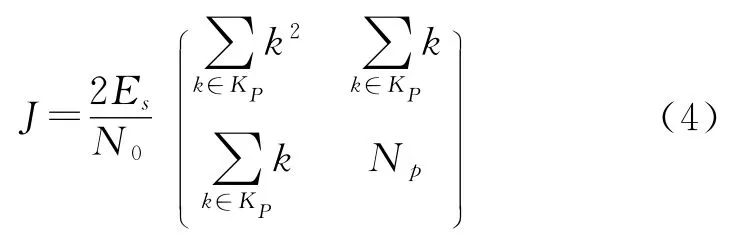
如果同時使用了導頻符號和數據符號，則Fisher矩陣變為［9］

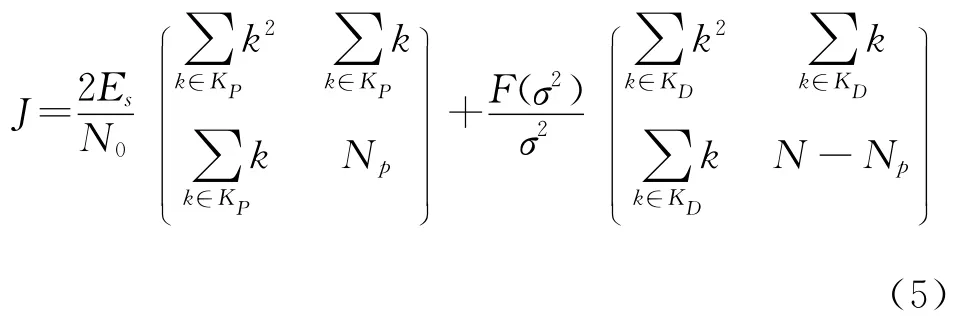
其中，KD是全部數據符號下標組成的集合。顯然有KP∩KD＝?及KP∪KD＝｛1，2，3，…，N｝。

從文獻［10］中可知F（σ2）／σ2的值為

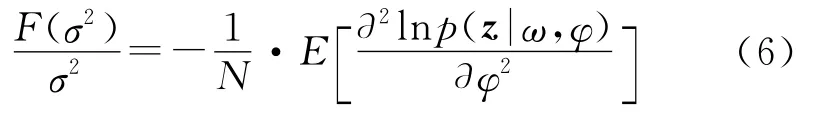
其中，p（z｜ω，φ）是概率密度函數，定義如下

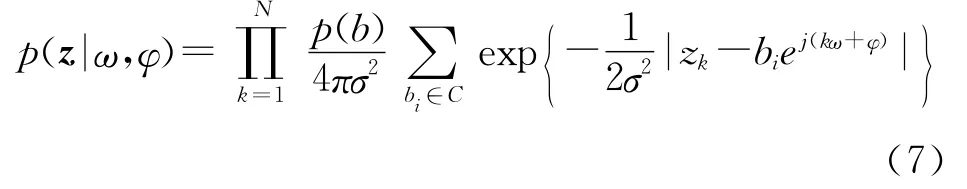
其中，平均能量為1的BPSK星座圖C＝｛－1，1｝，分布概率p（b）＝1／2。計算F（σ2）／σ2值的較快方式是使用蒙特卡洛法。

根據CRLBf的含義，頻偏試探間隔Δfd宜取值為CRLBf平方根的一半，即

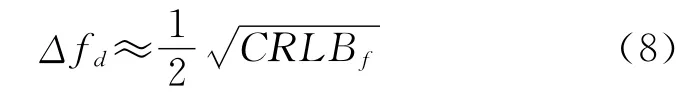
由于CRLBf的值與信噪比有關，所以本文是在平均意義上選取Δfd。歸一化頻偏fd的范圍（即｜fd｜max）可根據通信系統的參數計算得到。

傳統的最大似然函數為［2］

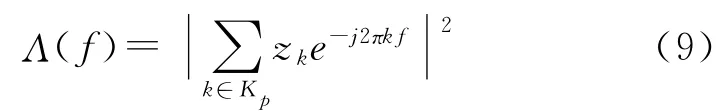
對式（9）進行改進，定義導頻似然函數Hp（f）為

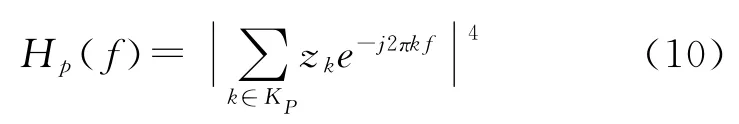
定義數據似然函數Hd（f）為

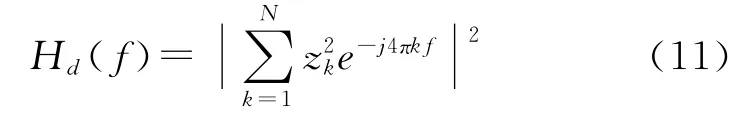
其中f在區間［－｜fd｜max，｜fd｜max］內，且以Δfd為間隔。為了硬件實現的方便，在式（10）和式（11）中進行了冪運算，使Hp（f）和Hd（f）的量綱一致化。

引入合并系數a，定義總似然函數H（f）為

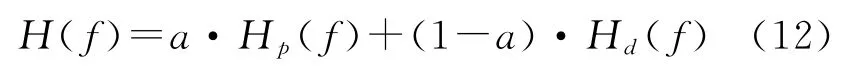
其中a滿足0≤a≤1。特別地，a＝1時為傳統的最大似然算法，只使用導頻符號、不使用數據符號；a＝0時則只使用數據符號、不使用導頻符號。

針對所有的試探頻偏值，都可以算出H（f）的值，使H（f）取最大值的fd就是頻偏估計結果。

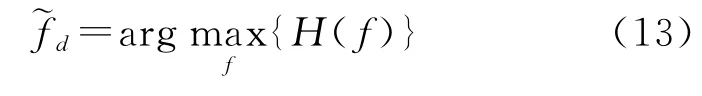
合并系數a的取值會影響算法的性能。對于給定的導頻結構，需要挑選出最合適的a，這個過程可由預先仿真完成。

為了對比，下面給出M＆M算法的表達式，定義自相關函數為

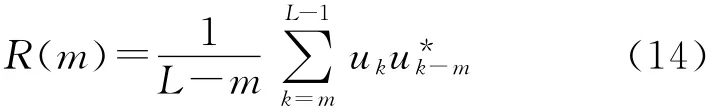
其中uk（1≤k≤N）表示導頻符號。

從文獻［7］可知，M＆M算法的頻偏估計結果為

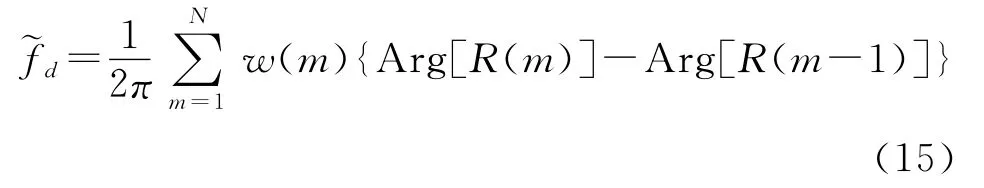
其中w（m）為平滑函數

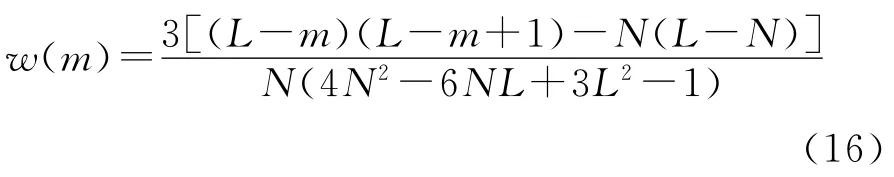
其中1≤N≤L－1，典型情況下N＝L－1。

3 仿真

3.1 仿真條件

為了驗證新算法的性能，進行三次仿真。首先對歸一化頻偏的估計范圍進行仿真，設定歸一化頻偏的范圍為（－0.5，0.5），信噪比設為2dB。

第二個仿真針對不同合并系數a條件下的頻偏估計性能。設fd均勻分布于（－0.01，0.01），載波初相位θ均勻分布于（－π，π］。歸一化頻偏0.01是比較接近實際情況的，因為接收機前端往往已經消除了大頻偏，殘余頻偏比較小，一般不會超過0.01。通過改變a的值，考察新算法性能的變化，從而挑選出最佳的a。信噪比設為－8dB～－2dB，以1dB為步進。

第三個仿真將新算法與M＆M算法進行了對比，合并系數a設為0.4。仿真中考慮了兩種M＆M算法，一種只利用導頻符號，另一種則同時利用到導頻符號和數據符號，其中數據符號進行了平方運算以消除調制信息。由于數據符號平方之后的信噪比非常低，所以需要對數據符號進行疊加，即把若干個數據符號之和視作一個符號。

新算法并不限定導頻圖案的任何形式，因此三個仿真中都使用最常規的導頻圖案。幀長N＝500，導頻符號數Np＝100，且導頻符號全部放在幀頭。頻偏試探間隔Δfd≈3×10－5。

3.2 仿真結果

仿真圖1給出了新算法的估計范圍。從圖中可見，新算法的歸一化頻偏估計范圍達到了最大的（－0.5，0.5）。

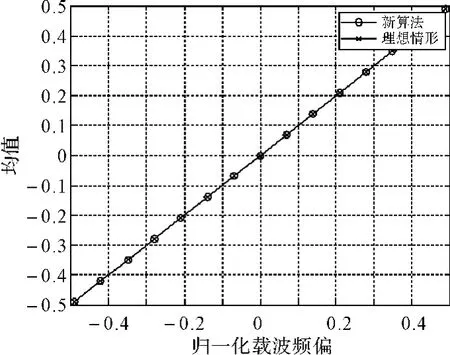
圖1 載波頻偏估計范圍

仿真圖2顯示了不同信噪比下的頻偏估計方差。從圖中可見，新算法的信噪比門限受到a值的影響。在給定的導頻圖案下，最佳的a＝0.4，此時信噪比門限達到－5dB，且估計方差接近CRLB。注意圖中有兩條CRLB曲線，傳統的最大似然估計算法（a＝1）達到了導頻符號估計的CRLB；新算法（最佳a＝0.4）達到了導頻符號和數據符號聯合估計的CRLB。

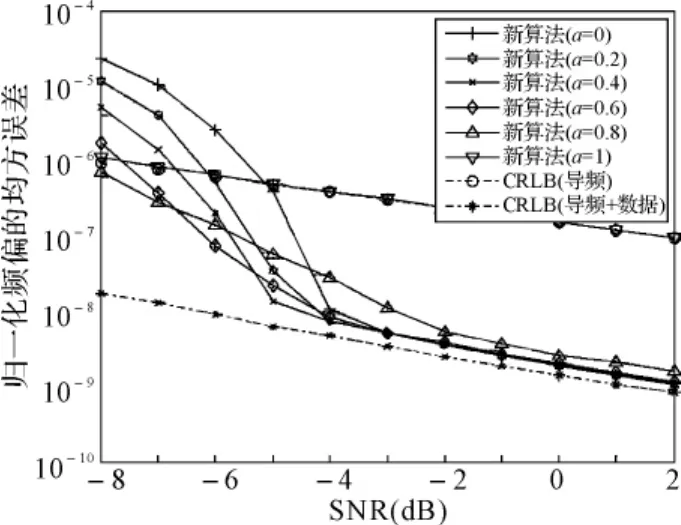
圖2 載波頻偏估計的均方誤差（不同a值條件下）

仿真圖3對比了新算法（a＝0.4）與M＆M算法的性能。從圖中看出，M＆M算法的信噪比門限為－1dB，新算法的信噪比門限為－5dB，新算法比M＆M算法改進了至少4dB。

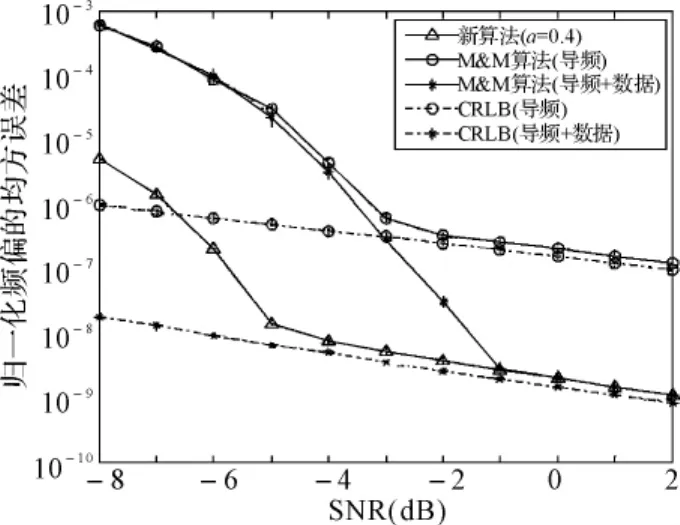
圖3 載波頻偏估計的均方誤差（新算法與M＆M算法對比）

新的載波頻偏估計算法只用到了加法運算和乘法運算，非常有利于在硬件上（如DSP、CPLD、FPGA等）實現，運算復雜度比FFT要小，估計性能也很好。此外，新算法可適用于任何導頻圖案，無論是規則的或不規則的。如果想提高估計速度，可以增大試探間隔Δfd，但也會降低估計精度。

本文的分析都在BPSK調制基礎上展開，但這并不代表新算法只適用于BPSK，事實上對于其他MPSK（M＞2）調制，新算法依然有效，只需修改式（10）和式（11）中的冪次即可。

4 結語

本文提出了一種適用于突發傳輸的新型載波頻偏估計算法，新算法利用了突發幀中的導頻符號和數據符號，具有較低的信噪比門限和較大的頻偏估計范圍，估計性能接近CRLB，而且運算復雜度低，非常實用。

［1］Sig Nele N，Heidi S，Moeneclaey M.Carrier phase tracking from Turbo and LDPC coded signals affected by a frequency offset［J］.IEEE Communications Letters，2005，9（10）：915.

［2］D.Rife，R.Boorstyn.Single tone parameter estimation from discrete time observations［J］.IEEE Trans Inform Theory，IT220，1974：591－598.

［3］S.M.Kay.A fast and accurate single frequency estimator［J］.IEEE Trans.Acoust.，Speech，Signal Pro－cessing，1989，37：1987－1990.

［4］Luke M，Reggiannini R.Carrier Frequency Recovery in All－Digital Modems for Burst－Mode Transmissions［J］.IEEE Transactions on Communications，1995，43（2／3／4）：1169－1178.

［5］M.P.Fitz.Planar filtered techniques for burst mode carrier synchronization［C］／／Proc.IEEE GLOBECOM'91，Phoenix，AZ，Dec.，1991：12.1.

［6］Bian Dongming，Zhang Gengxin，Yi Xinying.A maximum likelihood based carrier frequency estimation algorithm［J］.ICSP2000，2000，1：185－188.

［7］Mengali U，Morelli M.Data－aided frequency estimation for burst digital transmission［J］.IEEE Trans Commun，1997，45：23－25.

［8］Gansman J A，Krogmeier J V，Fitx M P.Single Frequency Estimation with Non－uniform Sampling［C］／／Signals，Systems and Computers，Pacific Grove，CA，USA：Conference Record of the Thirtieth Asilomar Conference，1996：399－403.

［9］Rice F.Carrier－Phase and Frequency－Estimation Bounds for Transmissions With Embedded Reference Symbols［J］.IEEE Transactions on Communications，2006，54（2）：221－225.

［10］Rice F，Cowley B，Moran B，et al.Cramer－Rao Lower Bounds for QAM Phase and Frequency Estimation［J］.IEEE Transactions on Communications，2001，49（9）：1582－1591.

A Carrier FrequencyOffset Estimation Algorithm for BPSK Burst Transmission

WANG Lin1XU Hongquan2
（1.Unit 2，No.92493Troops of PLA，Huludao 125000）（2.Navy Representative Office in Wuhan 709Institute，Wuhan 430205）

This paper proposes a new carrier frequency offset estimation algorithm in Binary Phase Shift Keying（BPSK）burst transmission based on pilot symbols and modulated data symbols.Its estimation range is large，which is about±0.5of the symbol rate.The simulation results show that this algorithm has low SNR threshold，and its estimation mean square error（MSE）is close to Cramer－Rao Lower Bound（CRLB）.The algorithm's computational complexity is low and it's very practical.

burst transmission，carrier synchronization，frequency offset estimation，Cramer－Rao lower bound

TN914.52DOI：10.3969／j.issn.1672－9730.2015.11.019

2015年5月17日，

2015年6月23日

王林，男，工程師，研究方向：武器裝備系統工程。許宏泉，男，碩士，高級工程師，研究方向：艦載指控系統、計算機應用。