基于區間攝動理論的隧道結構響應分析
丁健峻,薛齊文,劉旭東
(1.大連交通大學 土木與安全工程學院,遼寧 大連 116028;2. 北京機械設備研究所,北京 100854)
基于區間攝動理論的隧道結構響應分析
丁健峻1,薛齊文1,劉旭東2
(1.大連交通大學 土木與安全工程學院,遼寧 大連 116028;2. 北京機械設備研究所,北京 100854)
基于區間攝動理論,針對隧道結構不確定量,結合基于單元的有限元方法,建立了隧道結構區間求解模型.該模型采用8節點等參元進行離散,同時考慮物理參數不確定性、材料非均質不確定性和荷載不確定性,利用區間有限元方法,對模型進行了不確定性分析,得到了隧道結構靜力響應的區間范圍,并將結果與ANSYS軟件分析結果相對比.數值結果表明該模型在求解隧道結構不確定性問題是有效的、可行的.
響應分析;不確定性;區間攝動理論;區間有限元
0 引言
巖土工程是一個高度復雜的不確定和不確知系統,在以往的分析中,學者們將結構參數、初始條件及邊界條件等均視為確定量進行分析求解,使結果存在一定的誤差甚至是錯誤.近年來,隨著全國各地高速公路、高速鐵路的飛速發展,加之科學技術以及人們環境保護意識的增長,以往高挖高填的施工、設計工藝越來越不能滿足人們的各項需求,隨之而來的是隧道工程在工程實際中所占比例提高.近年來許多學者投身于隧道結構的研究中去,但多是基于確定性進行分析研究的.為了得到更加準確且對工程實際有指導意義的分析結果,對于隧道結構不確定性問題的研究尤為重要.
針對不確定性問題的不同類型,目前主要存在三種方法進行求解:隨機模型、模糊模型、區間分析模型[1].區間分析模型,無需依賴大量統計數據來描述不確定參數的概率分布或者隸屬函數,僅需通過不確定參數的取值范圍,便能求解出響應的區間范圍,更加符合工程實際.這有助于該模型在工程實際應用中的推廣,區間攝動理論在區間模型求解過程中也能很好的提高求解效率,減少計算成本.區間分析模型在其他領域應用較廣,并且取得了很多成果[2-4],但對于隧道結構的應用而言還相對較少.
鑒于以上原因,本文基于區間攝動理論,結合基于單元的有限元方法,建立了隧道結構求解模型,將隧道結構及其周圍巖土視為半無限體,同時考慮物理參數、初始條件及所用材料的不確定性對該結構模型進行靜力響應分析,給出了相應的數值算例,將不確定性計算結果與ANSYS軟件分析出的確定性結果相對比.計算結果表明,所提數值求解模型在對隧道結構靜力響應不確定性問題進行分析時有良好的精度是有效的、可行的.
1 有限元模型
基于單元的有限元控制方程[3]:
KU=F
(1)
引入區間攝動理論,其中:
將式(1)展開后可得到基于區間攝動理論的單元的有限元方程:
(2)
即,可將工程分解成確定性部分和不確定性部分:
FC=KCUC
(3)
(4)
忽略高階項得:
(5)
將式(3)和(5)利用數學變換后可得:
(6)
(7)
令ΔU=ΔU1即得到位移的1階攝動解:
(8)
將式(8)帶入式(4)并舍去高階項整理后可得位移的2階攝動解:
(9)
同理亦可得到位移的n階攝動解,由此可知
(10)
其中,K代表結構剛度陣,U為結構位移列向量,F為外荷載列向量,ΔK,ΔU,ΔF表示相應參數的微小攝動量.
由此,通過區間攝動理論,將式(1)分離成表達形式均為確定性形式的確定性部分式(3)和不確定性部分式(4),得到1階攝動解式(8)與2階攝動解式(9),同理亦可推算出n階攝動解,本文計算中,通過聯立方程式(3)和式(5),求解算例,推算至位移響應的三階攝動解,一定程度上提高了計算結果的精度.
2 模型建立
如圖1所示,結構底邊長10.6m,高11.3m,厚度選取為單位厚度, 隧道弧頂半徑為2m, 寬4m,高5m,隧道結構襯砌部分厚度為0.3m,隧道路基填筑為1m.
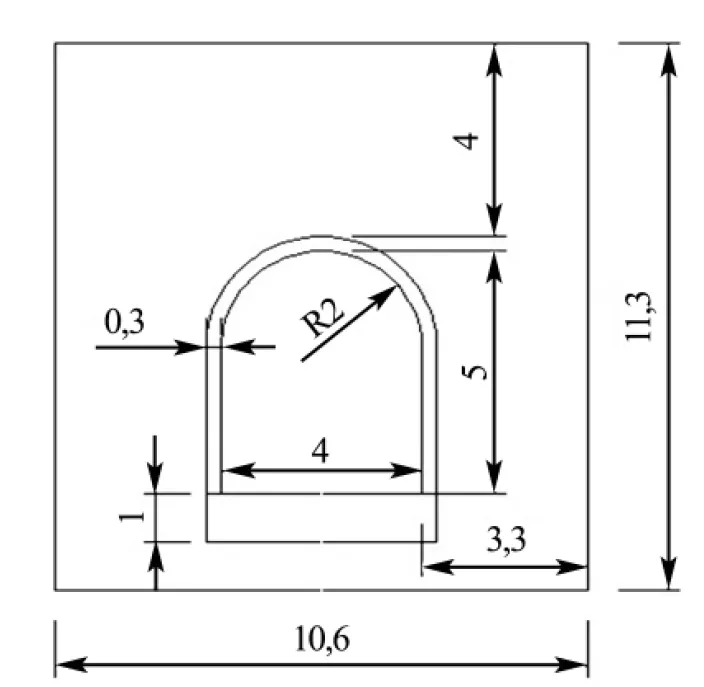
圖1 隧道模型
結構劃分時采用8節點等參元進行網格劃分,共計劃分88個單元,316個節點,為方便分析,選取測點1,2,3,4,5,6,如圖2所示.計算時,考慮結構為半無限體,對除結構頂邊外的其余三邊上各節點進行全約束,即Ux=Uy=0.
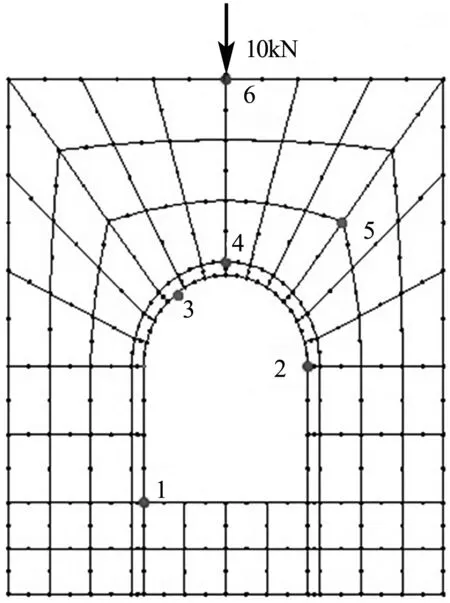
圖2 模型單元劃分及測點分布
3 算例
考慮隧道結構的區間靜力問題,如圖1所示的隧道結構,網格劃分及測點分布如圖2所示,考慮結構的各物理參數、初始條件為區間變量時,分析該截面測點的區間靜力位移響應問題,并將計算結果與ANSYS分析的確定性結果相對比.
算例1 在結構頂端施加一恒定荷載F=10kN,對圖中所示各點進行位移響應分析.假設確定性情況下彈性模量E=2 000MPa,泊松比μ=0.3.計算結果見表1,表2.
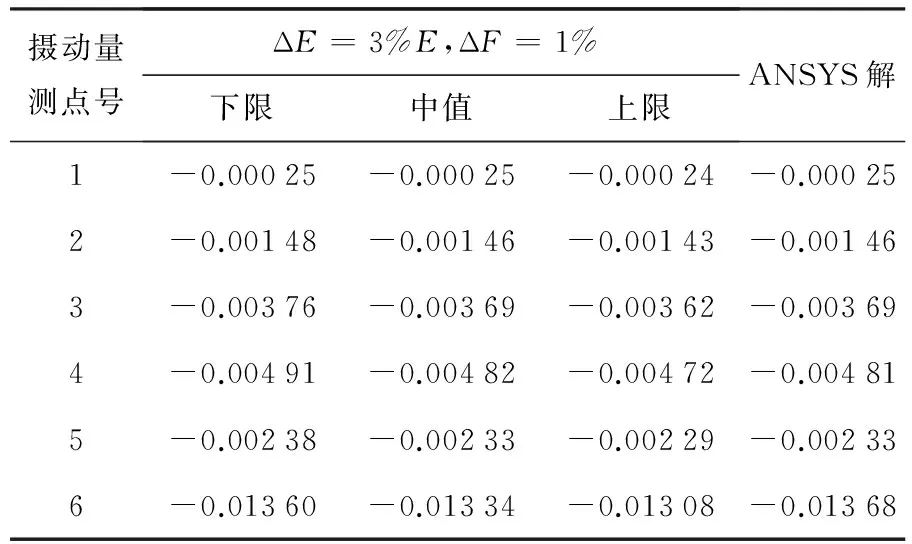
表1 區間計算結果1
注:表中位移單位為mm,下表同
由表1,表2可知,結構參數區間范圍的改變并不影響區間中值的計算結果,僅改變區間結果的范圍大小,這與前文公式相一致.區間中值計算結果與ANSYS分析結果基本一致,能較好的滿足計算精度.
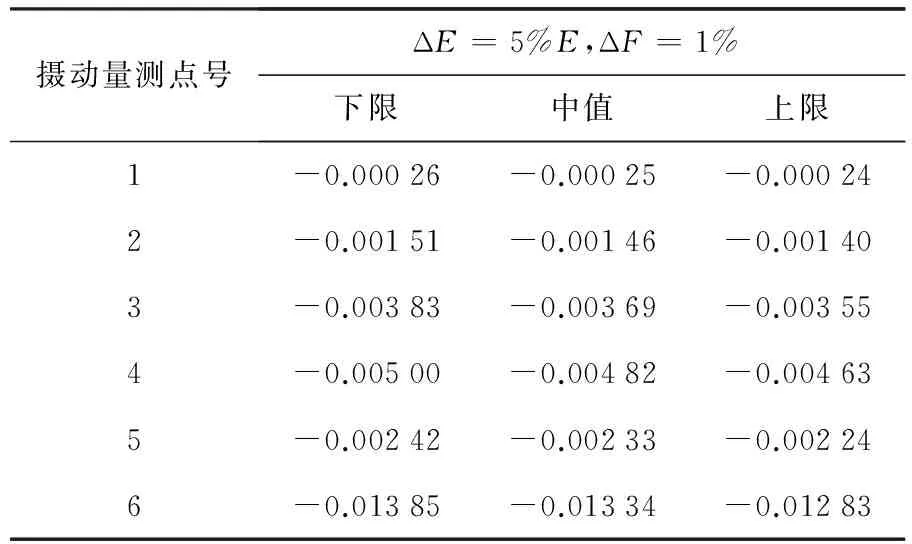
表2 區間計算結果2
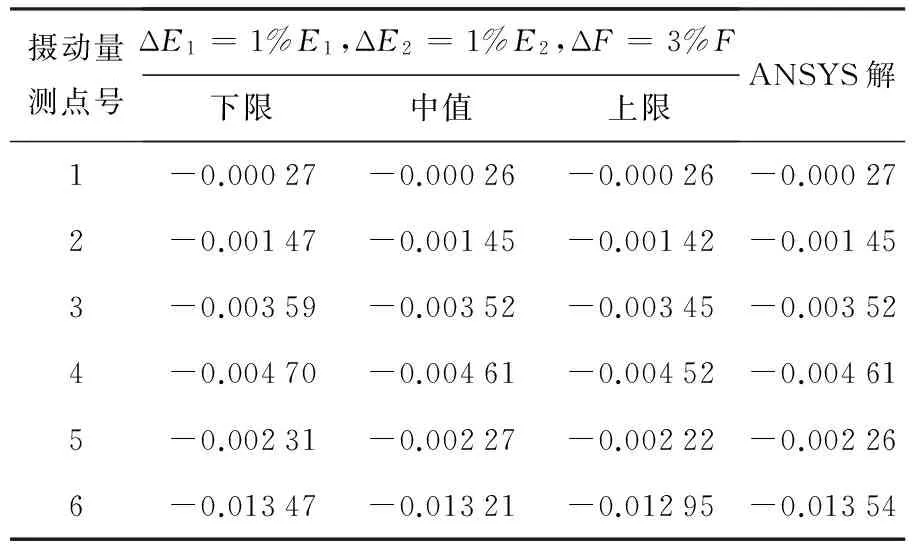
表3 區間計算結果3
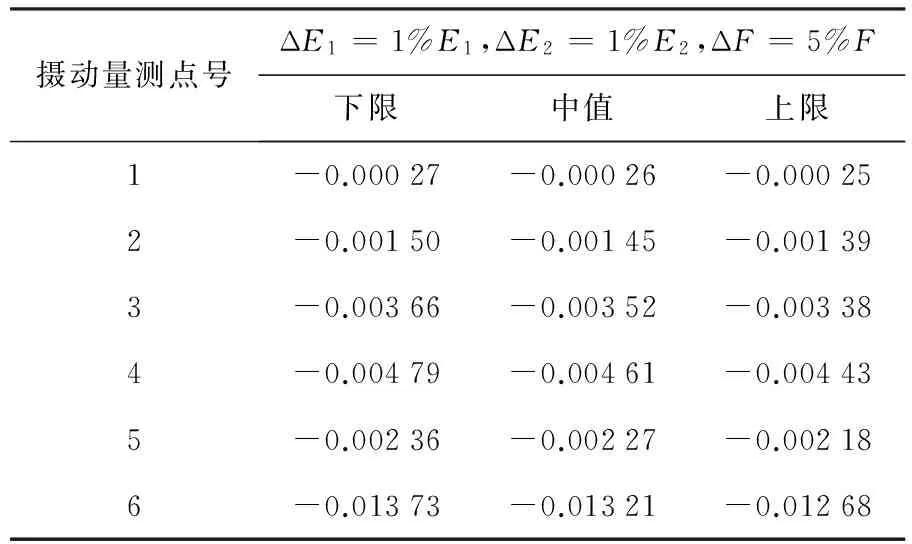
表4 區間計算結果4
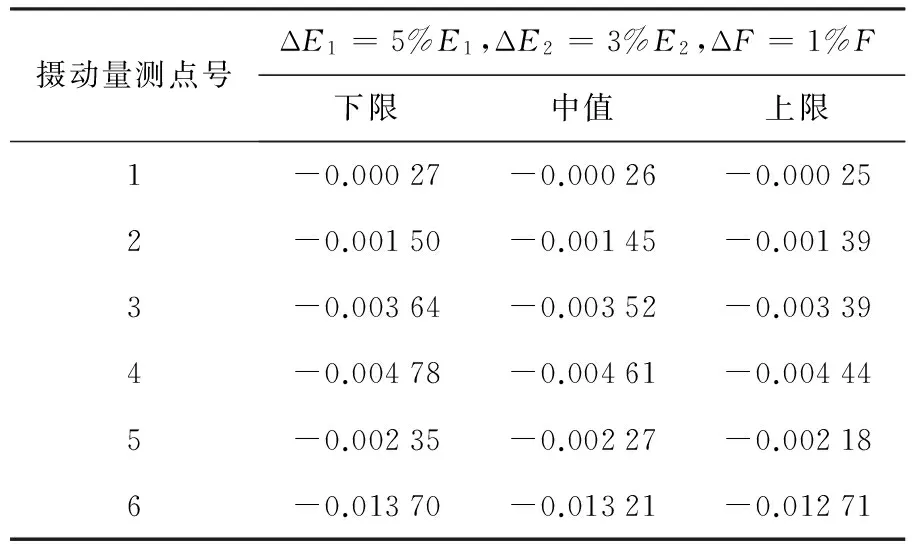
表5 區間計算結果5
算例2 在結構頂端施加一恒定荷載F=10kN,假設在確定性情況下,襯砌結構及隧道路基的彈性模量E2為3 000MPa,其余部位彈性模量E1為2 000MPa,泊松比μ皆為0.3.計算結果見表3~表5.
由表3~表5可知,當考慮材料參數的不均勻性時,計算結果同樣滿足前文公式,區間范圍大小的改變并不影響區間中值結果,僅對區間結果的范圍有影響,并且區間中值計算結果與ANSYS分析結果基本一致,進一步驗證了該模型對于隧道結構不確定性靜力分析的有效性與可行性.
4 結論
本文將區間攝動理論與有限元方法相結合,針對結構的靜力問題,對具有區間參數的隧道結構靜力響應問題進行了分析.通過數值算例,驗證了所建立的數值計算模型在計算具有區間參數的隧道結構靜力響應問題的分析和求解中的有效性和可行性,并且有良好的計算精度,有望于進一步對動力問題進行研究.
[1]蘇靜波,邵建國.基于區間分析的工程結構不確定性研究現狀與展望[J].力學進展,2005,35(3):338-344.
[2]杜秀云,唐禎安,薛齊文.瞬態熱傳導溫度場不確定性區間數值分析[J].功能材料,2013,44(11):1558-1561.
[3]蘇靜波.工程結構不確定性分析及其工程研究[D].南京:河海大學,2006.
[4]SHAO GUOJIAN,SU JINGBO.Interval Finite Element Method and Its Application on Anti-Slide Stability Analysis[J]. Applied Mathematics and Mechanics (English Edition),2007,28(4):521-529
[5]GUO SHUXIANG,LV ZHENZHOU.Interval Arithmetic and Static Interval Finite Element Method[J]. Applied Mathematics and Mechanics(English Edition),2001,22(12):1390-1396.
[6]蘇靜波,邵國建,劉寧.基于單元的子區間攝動有限元方法研究[J].計算力學學報,2007,24(4):524-528.
Tunnel Structure Response Analysis based on Interval Perturbation Theory
DING Jianjun1,XUE Qiwen1,LIU Xudong2
(1.School of Civil and Safety Engineering,Dalian Jiaotong University,Dalian 116028,China;2.Beijing Insititute of Machinery and Equipment,Beijing 100854,China)
A numerical model is established on the basis of combining finite element method and the interval perturbation theory to solve uncertainty problem for the tunnel structure. This model discrete by 8-node isoparametric element,and is solved by the interval finite element method considering the physical parameter uncertainty,the material heterogeneity uncertainty and the load uncertainty.The effectiveness and feasibility of the model is proved by the comparison of the interval analysis results with certainty results with ANSYS.
response analysis;uncertainty;interval perturbation theory;interval finite element method
1673- 9590(2015)01- 0068- 04
2014-01-31
丁健峻(1986-),男,碩士研究生;薛齊文(1976-),男,教授,博士,主要從事傳輸反問題、計算力學的研究
A
E- mail:sanji_911@163.com.

