幾何代數(shù)GIS計算引擎的設(shè)計與實現(xiàn)
胡 勇,孫 惠,羅 文,袁 林 旺
(1.南京師范大學(xué)計算機(jī)科學(xué)與技術(shù)學(xué)院,江蘇 南京 210023;2.南京師范大學(xué)虛擬地理環(huán)境教育部重點實驗室,江蘇 南京 210023)
?
幾何代數(shù)GIS計算引擎的設(shè)計與實現(xiàn)
胡 勇1,2,孫 惠2,羅 文2,袁 林 旺2
(1.南京師范大學(xué)計算機(jī)科學(xué)與技術(shù)學(xué)院,江蘇 南京 210023;2.南京師范大學(xué)虛擬地理環(huán)境教育部重點實驗室,江蘇 南京 210023)
分析型GIS的發(fā)展對GIS開發(fā)模式的統(tǒng)一性和算法的通用性提出了新的要求。基于幾何代數(shù)(GA)的GIS多維統(tǒng)一計算模型(GA-MUC)為進(jìn)行復(fù)雜GIS空間分析提供了解決思路。該文提出了基于GA的多維統(tǒng)一GIS計算引擎(GA-MUCE),探討了基于GA的屬性空間、網(wǎng)絡(luò)空間與場空間中基本對象與算子的表達(dá),并將其用于GIS算法的構(gòu)建。該引擎具有自適應(yīng)性特征,可根據(jù)具體的應(yīng)用需求定義計算空間,進(jìn)而設(shè)計相應(yīng)的對象表達(dá)與算子、算法庫,最終構(gòu)建插件形式的GIS分析求解模板。該研究是對復(fù)雜GIS空間分析問題求解模式的探索,有利于促進(jìn)新一代分析型GIS的發(fā)展。
幾何代數(shù)(GA);GA-MUC;計算引擎;計算插件
0 引言
隨著物聯(lián)網(wǎng)及大數(shù)據(jù)時代的到來,海量、動態(tài)、非結(jié)構(gòu)化的多源空間數(shù)據(jù)的分析已成為當(dāng)今及未來GIS發(fā)展的核心[1],迫切需要發(fā)展以空間多要素分析與服務(wù)為核心,可有效支撐海量數(shù)據(jù)分析與過程模擬的“分析型GIS”。相對于傳統(tǒng)的以數(shù)據(jù)為核心的“管理型GIS”,“分析型GIS”要求能應(yīng)對不同來源、不同類型、海量地理時空數(shù)據(jù)的整合分析,并要求在分析算法層面上支撐大規(guī)模、多維數(shù)據(jù)的高效計算。但現(xiàn)有GIS空間數(shù)據(jù)的計算規(guī)則與分析方法相對滯后,在多維對象的自適應(yīng)表達(dá)、空間數(shù)據(jù)的統(tǒng)一分析及多維統(tǒng)一分析框架的構(gòu)建方面仍顯不足,亟須發(fā)展一套相對通用的GIS算法模板以及統(tǒng)一的系統(tǒng)開發(fā)模式,使得海量數(shù)據(jù)資源得到有效利用。
幾何代數(shù)(GA)是一種結(jié)合代數(shù),實現(xiàn)了不同代數(shù)系統(tǒng)的有效統(tǒng)一與集成[2],從而為包含不同地理要素表達(dá)和各類GIS數(shù)據(jù)互操作的計算空間的構(gòu)建提供了可能。多重向量結(jié)構(gòu)對混合維度幾何對象與語義結(jié)構(gòu)的統(tǒng)一組織與表達(dá),為相關(guān)空間數(shù)據(jù)的組織、存儲與運算提供了原生的數(shù)學(xué)與數(shù)據(jù)結(jié)構(gòu)[3];幾何代數(shù)算子的統(tǒng)一性也可實現(xiàn)不依賴于坐標(biāo)的幾何關(guān)系計算[4],從而為包含空間、語義等多要素的GIS對象的自適應(yīng)表達(dá)、動態(tài)更新與關(guān)系計算提供了有利支撐。袁林旺等提出了基于幾何代數(shù)的GIS多維統(tǒng)一計算模型(GA-MUC)[5],并在三維GIS空間數(shù)據(jù)建模[6]、多維統(tǒng)一GIS計算[7]和場數(shù)據(jù)特征分析[5]等領(lǐng)域得到應(yīng)用。以上研究為基于幾何代數(shù)的GIS計算提供了理論上的推導(dǎo)與應(yīng)用驗證。本文基于GA-MUC框架,利用幾何代數(shù)空間中的基本表達(dá)與算子構(gòu)建直接面向GIS計算的對象表達(dá)與運算,設(shè)計了基于幾何代數(shù)的屬性空間、網(wǎng)絡(luò)空間與場空間的表達(dá),并對上述空間中對象表達(dá)與計算算子的生成規(guī)則進(jìn)行探討,進(jìn)而構(gòu)建了基于幾何代數(shù)的多維統(tǒng)一計算引擎(GA-MUCE),并給出具體的系統(tǒng)實現(xiàn)流程和案例示范。
1 理論基礎(chǔ)與GA-MUCE設(shè)計框架
1.1 幾何代數(shù)多重向量表達(dá)與算子運算
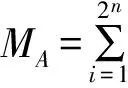
在幾何代數(shù)系統(tǒng)中,幾何積的不可逆性是其可用于幾何問題求解的基礎(chǔ)[4]。同時利用幾何積還可構(gòu)建其它更為復(fù)雜的幾何關(guān)系運算,此類運算被稱為GA算子。對于給定多重向量MA和MB,可定義二者間的運算“°”為:
(1)
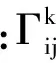
1.2GA-MUCE設(shè)計層次框架
構(gòu)建基于幾何代數(shù)的多維統(tǒng)一GIS計算引擎(GA-MUCE)三層架構(gòu)如圖1所示:1)空間構(gòu)建層,主要實現(xiàn)GA空間定義。由于不同的GA模型其表達(dá)能力與運算能力不盡相同,同時考慮到空間的維度也會對后續(xù)算子構(gòu)建的復(fù)雜度和運算效率產(chǎn)生影響,GA空間的定義通常根據(jù)GIS數(shù)據(jù)和具體GIS分析需求制定。2)對象表達(dá)層,主要實現(xiàn)GIS數(shù)據(jù)到GA空間的嵌入,為常用的多維矢量數(shù)據(jù)、網(wǎng)絡(luò)數(shù)據(jù)與場數(shù)據(jù)分別制定表達(dá)結(jié)構(gòu)和轉(zhuǎn)換方法。在表達(dá)中不僅需要解決對象幾何與幾何結(jié)構(gòu)的嵌入,還需要考慮到地理屬性與語義關(guān)系的表達(dá)。3)算子生成層,該層主要利用GA空間中基本的算子、算法,結(jié)合GIS空間運算算法,構(gòu)建復(fù)合的GIS空間計算算子,并利用多重向量的計算規(guī)則將其向網(wǎng)絡(luò)空間和高維場空間擴(kuò)展,實現(xiàn)GIS空間計算算子集的構(gòu)建。
圖1 計算引擎層次結(jié)構(gòu)
Fig.1FrameworkofGA-MUCE
2 GA-MUCE構(gòu)建方法
2.1 基于GA的GIS空間表達(dá)
幾何代數(shù)空間的可定義性是其可用于不同GIS問題求解的重要前提。幾何代數(shù)空間的定義主要分為基向量的定義和度量特征定義兩個步驟。基向量的個數(shù)反映了對象維度,度量特征多是由基向量間的內(nèi)積矩陣確定。據(jù)內(nèi)積運算特點,可進(jìn)一步將其簡化為在i=j和i≠j兩種情況下,對ei·ej的限定[4]。度量特征可用于幾何代數(shù)運算規(guī)則及運算特性的定義。例如,在歐氏空間中內(nèi)積表示兩向量之間的模與其角度的乘積,而共形空間中內(nèi)積表示兩點之間距離平方的相反數(shù)。
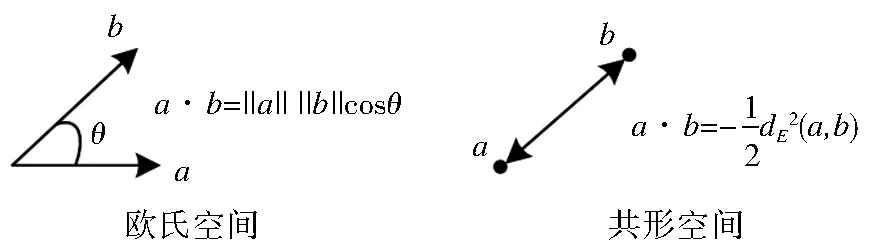
圖2 不同度量空間示例
Fig.2Samplesofdifferentmetricspaces
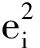
根據(jù)上述空間定義規(guī)則,定義可支持各類GIS數(shù)據(jù)計算的幾何代數(shù)空間,如表1所示。
2.2 基于GA的GIS對象表達(dá)
表1 常用GIS空間的GA表達(dá)
Table1TheGArepresentationsofthecommonGISspaces

GIS空間GA空間基向量度量定義幾何空間屬性空間網(wǎng)絡(luò)空間場空間歐氏空間e1,e2,…,ene2i=1,ei·ej=0齊次空間e0,e1,…,ene2i=1,ei·ej=0共形空間e0,…,en,e∞e0·e0=e∞·e∞=0,e0·e∞=-1n維屬性空間ea1,ea2,…,eaneai·eaj=0e2ai=1 ai為數(shù)值型e2ai=0 ai為字符,枚舉型{n維網(wǎng)絡(luò)空間ev1,ev2,…,evnevi∧evj=evivj 連通evi∧evj=0 不連通{n維張量空間e1+e2…+enA B=[aib1ei1,…,aibjeij]
在幾何代數(shù)空間中主要有blades和多重向量兩種表達(dá)方式,blades多用于表達(dá)單一維度對象,而多重向量則可實現(xiàn)混合維度對象的表達(dá),可用于構(gòu)建復(fù)雜的幾何體,或者實現(xiàn)包含語義、拓?fù)涞刃畔⒌亩嗑S復(fù)合表達(dá)。
在幾何表達(dá)空間中基本對象主要包括點、線、面、球等理想的幾何對象,由于GIS空間中對象均具有明確的邊界信息,并且多為復(fù)合結(jié)構(gòu),需要利用多重向量組合不同維度的blades;在網(wǎng)絡(luò)空間中表達(dá)連通性的節(jié)點、邊、路徑均可通過blades進(jìn)行表達(dá),其中當(dāng)grade為1時表示節(jié)點,grade為2時表示網(wǎng)絡(luò)的一條邊,grade大于2時表示路徑;場空間中的基本對象是向量的表達(dá),在其各自的嵌入空間中均為blade,但在整個張量空間中可表達(dá)為多重向量,并可通過多重向量在特定子空間的投影得到具有明確地理語義特征的blade結(jié)構(gòu),為復(fù)雜的地理分析提供支撐。基于GA的GIS對象表達(dá)示例見表2。
表2 基于GA的GIS對象表達(dá)示例
Table 2 The GA-based representation of GIS objects

GIS對象GA空間表達(dá)式線段n+2維共形空間L=A1∧A2射線n+2維共形空間R=A+ v三角形n+2維共形空間T=F+L1+L2+L3四面體n+2維共形空間Te=S+T1+T2+T3網(wǎng)絡(luò)節(jié)點n維網(wǎng)絡(luò)空間N=wvievi,w為權(quán)重網(wǎng)絡(luò)邊n維網(wǎng)絡(luò)空間E=wvivjevivj,w為權(quán)重含m個節(jié)點的路徑n維網(wǎng)絡(luò)空間P=wvx1,vx2,…,vxmevx1,vx2,…,vxm,w為網(wǎng)絡(luò)權(quán)重場向量n維張量空間V=a1e1+a2e2,…,+anen
注:A、F、S分別表示點、平面、球的共形幾何代數(shù)表達(dá)。
2.3 基于GA的GIS計算算子
GA算子所具有的對象無關(guān)特征及可重構(gòu)性是GIS空間計算算法構(gòu)建的基礎(chǔ),其特征內(nèi)蘊(yùn)的性質(zhì)為包含多信息要素的對象空間關(guān)系分析與求解提供了依據(jù),可在幾何代數(shù)基礎(chǔ)算子的基礎(chǔ)上構(gòu)建面向幾何、關(guān)系、網(wǎng)絡(luò)及場數(shù)據(jù)的求解算子(表3)。其中幾何度量包括對象間距離求解及對象自身模(體積、面積)的計算。基于上述幾何代數(shù)運算空間的定義,可以將上述度量指標(biāo)分別映射到幾何代數(shù)空間中的內(nèi)積和外積運算;幾何關(guān)系判斷包括同維度對象及不同維度對象的判斷,其中同維度對象可通過meet算子進(jìn)行判斷,不同維度對象需要先將低維對象投影至高維對象并判斷其同低維對象間外積的符號,當(dāng)其符號一致時表示在內(nèi)部,不一致則在外部[9];網(wǎng)絡(luò)空間中的網(wǎng)絡(luò)延拓算子由外積構(gòu)造,并嵌入了網(wǎng)絡(luò)連通性的判斷[10];場空間主要通過構(gòu)建梯度算子實現(xiàn)場特征參數(shù)的統(tǒng)一計算[11]。
表3 GA空間GIS計算算子
Table3TheGA-basedoperatorsofGIScomputation

分類算子表達(dá)式幾何度量關(guān)系判斷網(wǎng)絡(luò)空間算子場空間算子距離量算D(A1,A2)=κA1·A2模量算S( u, v)=τ u∧ v同維度對象QA1-A2=(meet(A1,A2)2>0)不同維度對象(點/三角形)QA-T=(sign(aiaj→∧aia→)≥0)網(wǎng)絡(luò)延拓算子mei∧nej=(m?n)eij,m、n為網(wǎng)絡(luò)權(quán)重場梯度算子grad(a)= Δalimτ→0f(x+εa)-f(x)ε
在歐氏幾何框架下,對象間距離、角度等空間關(guān)系的計算在不同維度對象上不統(tǒng)一,不同類型對象間的運算也需要分別處理,從而使得傳統(tǒng)算法適用性不強(qiáng),不利于設(shè)計面向動態(tài)場景和大規(guī)模數(shù)據(jù)的統(tǒng)一求解框架。GA框架下的幾何對象表達(dá)與計算對幾何度量關(guān)系具有內(nèi)蘊(yùn)性與繼承性,基于幾何代數(shù)的度量與關(guān)系表達(dá)更為簡潔且便于運算,同時利用GA算子對網(wǎng)絡(luò)空間和場空間的統(tǒng)一求解也有利于設(shè)計融合多種地理要素的復(fù)雜問題的算法。
3 GA-MUCE系統(tǒng)實現(xiàn)
3.1 系統(tǒng)實現(xiàn)流程
基于GA-MUCE的GIS實現(xiàn)主要包含GA-MUCE構(gòu)建模塊和GIS問題求解模塊兩部分(圖3),主要實現(xiàn)GIS數(shù)據(jù)的嵌入表達(dá)、GIS算法的幾何代數(shù)改造以及分析結(jié)果的投影與輸出等功能。
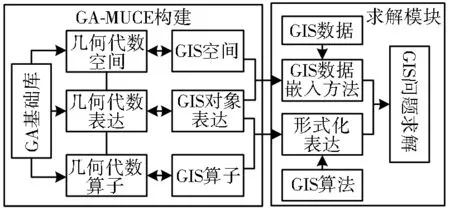
圖3 GA-MUCE實現(xiàn)流程
Fig.3 Implementation procedure of GA-MUCE
GA-MUCE構(gòu)建模塊主要包含基于幾何代數(shù)GIS空間的構(gòu)建、GIS對象的表達(dá)及GIS算子的設(shè)計三部分。它是GIS數(shù)據(jù)嵌入GA空間以及后續(xù)GIS空間問題求解的基礎(chǔ),主要通過建立GIS計算空間中的對象表達(dá)和運算,并利用GA計算軟件庫實現(xiàn)相關(guān)算法。目前已有一系列較為成熟的幾何代數(shù)計算庫,包括CLUCalc[12]、Gaigen[13]、Gaalop[14]和Gaalet[15]等。但上述算法庫大多面向幾何計算,缺少面向具體GIS數(shù)據(jù)的實現(xiàn)。考慮面向大規(guī)模GIS計算的效率優(yōu)化需求,選用較為高效的Gaigen 2.5作為本計算引擎中計算空間構(gòu)建模塊的核心計算庫,實現(xiàn)基于Gaigen的計算空間向GIS計算空間的映射。
GIS問題的求解模塊實現(xiàn)了GIS問題的幾何代數(shù)形式化表達(dá)與求解。幾何代數(shù)形式化表達(dá)需要在對現(xiàn)有算法充分解析的前提下,提煉出相應(yīng)的幾何代數(shù)求解模式,并將其轉(zhuǎn)換為可直接用于算子求解的代數(shù)表達(dá)。在模式提煉過程中需要充分考慮幾何代數(shù)表達(dá)與運算的統(tǒng)一性與求解過程的優(yōu)化,可利用Gaalop等GA表達(dá)式化簡庫對上述形式化表達(dá)加以優(yōu)化從而得出最高效的幾何代數(shù)算法。最后求得計算結(jié)果并將其反向投影回GIS空間。
綜上所述,構(gòu)建GA-MUCE的實現(xiàn)步驟如下:1)設(shè)定空間維度與基向量,定義基向量間的內(nèi)積矩陣,構(gòu)建度量空間;2)根據(jù)給定分析數(shù)據(jù)的組織方式,結(jié)合幾何代數(shù)空間定義,構(gòu)建歐氏空間向幾何代數(shù)空間的嵌入方法和幾何代數(shù)空間對象向歐氏空間投影方法;3)選取所要使用的GA算子與算法,結(jié)合GIS空間基本對象的空間度量與求解方法,設(shè)計基于幾何代數(shù)的GIS空間計算算子;4)分析需要求解的空間計算問題,對其傳統(tǒng)求解方法加以解析,并對其進(jìn)行幾何代數(shù)構(gòu)造,得到空間問題求解的幾何代數(shù)形式化表達(dá);5)優(yōu)化算法流程,求得最終結(jié)果。
3.2 GA空間與算子庫構(gòu)建
幾何代數(shù)是通過將低維度數(shù)據(jù)嵌入到高維數(shù)據(jù)從而獲得更高自由度的對象表達(dá)、運動表達(dá)與算子求解。但隨著空間維度的增加,在空間計算中所要處理的blade項迅速增多,導(dǎo)致算法復(fù)雜度增大,因而需要選取恰當(dāng)?shù)目臻g維度;同時考慮到不同幾何代數(shù)模型的度量特征不同,其所能構(gòu)建的算子也不盡相同,在幾何代數(shù)空間的構(gòu)建過程中要根據(jù)具體的分析需求定義不同的幾何代數(shù)空間模型,并選用合適的計算算子。為了保證幾何代數(shù)空間定義的靈活性,可通過配置文件構(gòu)建計算空間。首先設(shè)計幾何代數(shù)空間構(gòu)建所需要的空間基本信息、空間基向量以及空間度量設(shè)置,進(jìn)而列出在算法中應(yīng)用到的所有算子(圖4a)。利用上述配置文件結(jié)合Gaigen生成可執(zhí)行的C++代碼。
由于GIS對象多包含邊界、紋理等語義信息,需要將幾何代數(shù)空間中由子空間所表達(dá)的基礎(chǔ)對象擴(kuò)展為可用于GIS空間運算的幾何對象,該過程可通過組合GA基本對象實現(xiàn)。圖4b示例了GIS空間中點對象和射線對象的表達(dá)。不同于基礎(chǔ)GA對象,點對象在包含點坐標(biāo)的同時,還要給出其切平面(用于計算法向量)和紋理坐標(biāo)(紋理渲染與可視化);而射線對象和三角形對象即是在FreeVector對象和Plane對象的基礎(chǔ)上分別添加了端點約束和邊界約束。圖4b列舉了對基于GA基本算子的GIS計算算子的擴(kuò)展方法。對于射線,其基于端點的反射算子可進(jìn)一步解析為:在保留原始射線端點的前提下,對其方向向量應(yīng)用GA反射算子,同理可推導(dǎo)出三角形rotor變換算子。
3.3 算法插件的設(shè)計與系統(tǒng)嵌入
算法構(gòu)建層的主要工作是實現(xiàn)傳統(tǒng)GIS算法的幾何代數(shù)形式化表達(dá)并對GA表達(dá)的流程進(jìn)行簡化,最后求得運算結(jié)果。基于GA表達(dá)與算子的統(tǒng)一性,可設(shè)計相對通用的GIS表達(dá)與計算框架。在此框架下的GIS問題的形式化求解流程具有統(tǒng)一性,因而可設(shè)計基于GA-MUCE的算法模板,并通過插件方式嵌入到系統(tǒng)中。首先設(shè)計算法模板(圖4c),同時在系統(tǒng)API中設(shè)置相應(yīng)的插件接口類,實現(xiàn)對所綁定模板參數(shù)的輸入、輸出,同時設(shè)計對模板空間轉(zhuǎn)換函數(shù)及算法實現(xiàn)函數(shù)的事件調(diào)用,最終實現(xiàn)空間計算算法的插件形式嵌入與求解。
3.4 系統(tǒng)開發(fā)與實現(xiàn)
利用上述特性,設(shè)計了插件模式的GIS:基于幾何代數(shù)的多維空間計算系統(tǒng)(圖4d),實現(xiàn)了基本GIS空間數(shù)據(jù)的管理,利用幾何代數(shù)計算引擎對GIS空間計算提供算子與算法支撐,并通過插件的思路構(gòu)建特定的GIS分析功能。
系統(tǒng)窗體與控件利用WxWidget庫實現(xiàn),利用OpenGL和VTK分別實現(xiàn)多維矢量數(shù)據(jù)渲染及多維時空場數(shù)據(jù)的可視化;在應(yīng)用程序接口中主要實現(xiàn)了三種基本數(shù)據(jù)的管理與運算,并提供了GIS空間求解模型接口,實現(xiàn)插件形式的GIS空間計算模塊的集成。
4 結(jié)論
Fig.4 System implementation of GA-MUCE
本文介紹了基于幾何代數(shù)的GIS計算引擎(GA-MUCE)設(shè)計與程序?qū)崿F(xiàn),提出了基于GA的GIS計算空間構(gòu)建、GIS對象表達(dá)和GIS算子構(gòu)建的計算引擎三層架構(gòu)。在對多維矢量數(shù)據(jù)、網(wǎng)絡(luò)數(shù)據(jù)與高維場數(shù)據(jù)的表達(dá)與運算特征梳理的基礎(chǔ)上,構(gòu)建了基于幾何代數(shù)的幾何空間、屬性空間、網(wǎng)絡(luò)空間與場空間表達(dá)與運算。最后提出了基于配置文件的幾何代數(shù)空間定義方法和基于封裝的GIS對象與算子構(gòu)建方法,并基于幾何代數(shù)算法的靈活性與統(tǒng)一性,在對現(xiàn)有計算流程分析的基礎(chǔ)上,設(shè)計了插件嵌入的算法集成機(jī)制。利用配置文件可定義出合適的幾何代數(shù)空間,GIS空間計算算法則可通過插件的形式嵌入與擴(kuò)展,表明本文構(gòu)建的計算引擎具有較好的可定制性和可擴(kuò)展性。
[1] GOODCHILD M F.Citizens as sensors:The world of volunteered geography[J].GeoJournal,2007,69(4):211-221.
[2] HESTENES D,SOBCYK G.Clifford Algebra to Geometric Calculus[M].Heidelberg:Springer-Verlag,1984.
[3] PERWASS C.Geometric Algebra with Applications in Engineering[M].Berlin,Heidelberg:Springer-Verlag,2009.
[4] DORST L,FONTIJNE D,MANN S.Geometric Algebra for Computer Science:An Object-Oriented Approach to Geometry[M].San Francisco:Morgan Kaufmann Publishers,2009.
[5] YUAN L W,YU Z Y,LUO W,et al.Geometric algebra for multidimension-unified geographical information system[J].Advances in Applied Clifford Algebras,2013,23(2):497-518.
[6] YUAN L W,YU Z Y,LUO W,et al.A 3D GIS spatial data model based on conformal geometric algebra[J].Science China Earth Sciences,2011,54(1):101-112.
[7] YUAN L W,LV G,LUO W,et al.Geometric algebra method for multidimensionally-unified GIS computation[J].Chinese Science Bulletin,2012,57(7):802-811.
[8] AERTS D,MAREK C.Tensor-product versus geometric-product coding[J].Physical Review A,2008,77(1):012316.
[9] 宗真,袁林旺,羅文,等.三角網(wǎng)求交的共形幾何代數(shù)算法[J].測繪學(xué)報,2014,43(2):200-207.
[10] 俞肇元,胡勇,朱曉林,等.基于幾何代數(shù)的多類型約束路網(wǎng)最優(yōu)路徑分析算法[J].地理與地理信息科學(xué),2014,30(2):10-15.
[11] 羅文,袁林旺,俞肇元,等.多維向量場特征參數(shù)的幾何代數(shù)統(tǒng)一計算方法[J].系統(tǒng)工程理論實踐,2013,33(9):2390-2396.
[12] PERWASS C.CLUCalc 2014.Available:http://www.clucalc.info/.2013-12-30.
[13] FONTIJNE D.Gaigen 2.5:Geometric Algebra Implementation Generator[R].2010.1-112.
[14] HILDENBRAND D.Foundations of Geometric Algebra Computing[M].New York:Springer,2013.
[15] SEYBOLD F,UWE W.Gaalet-a C++ expression template library for implementing geometric algebra[C].6th High-End Visualization Workshop.Austria:Obergurgl,2010.1-10.
Design and Realization of GA Based Multi-dimensional Integrated GIS Computing Engine
HU Yong1,2,SUN Hui2,LUO Wen2,YUAN Lin-wang2
(1.DepartmentofComputerScienceandTechnology,NanjingNormalUniversity,Nanjing210023;2.KeyLaboratoryofVGE,MinistryofEducation,NanjingNormalUniversity,Nanjing210023,China)
The development of analysis-oriented GIS requires GIS systems make much more progress to follow certain templates and GIS algorithms to deal with different types of geographic data and data in different dimensions.GA based multi-dimensional unified computation model (GA-MUC) provides a solution for complicated GIS spatial analysis.In this paper,the GA based multi-dimensional unified computing engine (GA-MUCE) is designed,and the expressions of basic objects and operators in GA-based attribute space,network space and field space are discussed respectively.Then these methods are applied to the construction of GIS algorithms.The engine is able to meet different application meets.It can be used to define the computing space,design operator and algorithm libraries,express specific GIS objects,and finally construct the GIS analyzing templates in the form of plugin.Researches have been done to explore solutions for complex GIS spatial analysis in the paper,which will help to promote the development of new generation of analysis-oriented GIS.
geometric algebra (GA);GA-MUC;computing engine;computing plugin
2014-08-28;
2014-10-23
江蘇省高校自然科學(xué)研究項目“多維統(tǒng)一的幾何代數(shù)并行空間索引研究”(13KJB170006);江蘇省自然科學(xué)基金青年基金項目“復(fù)雜場景中空間關(guān)系動態(tài)計算的幾何代數(shù)方法”(BK2012454);國家科技支撐計劃課題“視頻GIS與突發(fā)公共事件的感知控制系統(tǒng)”(2012BAH35B02)
胡勇(1973-),男,碩士,講師,主要從事計算機(jī)算法設(shè)計與GIS應(yīng)用研究。E-mail:huyong@njnu.edu.cn
10.3969/j.issn.1672-0504.2015.01.006
P208;TP301.6
A
1672-0504(2015)01-0027-05

