大修改結構特征向量重分析的混合基展開法*
劉志軍, 鄧兆祥
(中國汽車工程研究院汽車噪聲振動和安全技術國家重點實驗室 重慶,400039)
大修改結構特征向量重分析的混合基展開法*
劉志軍, 鄧兆祥
(中國汽車工程研究院汽車噪聲振動和安全技術國家重點實驗室 重慶,400039)
為拓展基于矩陣攝動理論的結構重分析方法在實際工程中的適用范圍,提高重分析計算精度,針對結構模態空間不完備和參數大修改提出了結構動力重分析的混合基展開法。利用已知的少數幾個可能不連續的低階模態構造出整個模態空間的一個混合基,同時將反映結構參數改變的質量矩陣和剛度矩陣的增量表示為高次增量形式,保留了經典攝動法簡單易行的特點。數值算例表明,所提出方法適用范圍廣,極大提高了結構大修改下的動力重分析計算精度。
結構動力重分析; 結構大修改; 矩陣攝動法; 混合基展開法
引 言
結構動力修改和結構優化設計需要快速而高效的重分析技術來減少計算成本,提高工作效率。國內外許多學者對快速重分析的計算方法做過研究。矩陣攝動法[1]在結構重分析中經常使用,在此基礎上有理逼近法[2-4]、Shanks變換[5]、Epsilon算法[6-7]和動力縮聚與瑞利商法[8]等,被用來提高重分析的精度。近年來,組合近似法因其簡單、通用和高效等優點在很多領域得到應用并獲得不斷改進[9-14]。對實際的大型工程結構,要求出其全部模態,計算量非常龐大,往往只求得其少數低階模態。基于實驗模態的結構修改存在著實驗模態難以測全和很難保證所測得的各階模態為連續低階模態的問題。在這些情況下,現有的基于全模態展開的重分析方法根本無法實現。文獻[15]基于傳統矩陣攝動理論,將已知的有限低階模態擴充得到N維歐氏空間的一個混合基,并將特征向量的攝動量在新基上展開來計算特征向量的1,2階攝動量。但是,傳統經典攝動法僅適用于結構的小修改重分析,當結構參數修改較大時,計算精度變差,甚至變得沒有意義[1]。
筆者從經典矩陣攝動理論出發,首先,采用高次增量法將反映結構參數改變的質量矩陣和剛度矩陣的增量分別表示為小參數ε的1次與2次冪項之和;其次,利用已知的少數幾個低階模態構造出整個模態空間的一個混合基,把特征向量的攝動量表示為該混合基的線性組合;最后,推導得到孤立特征值及特征向量的2階攝動解,極大提高了結構大修改下的重分析計算精度。
1 矩陣攝動法
離散結構振動特征值問題為

(1)
其中:K為剛度矩陣;M為質量矩陣;λ=ω2;u為振型向量。
設結構修改后的質量矩陣、剛度矩陣表示為
(2)
(3)
其中:ε為小參數,與ε=0對應的系統稱為原系統;M0和K0為原結構的質量矩陣和剛度矩陣;εM1+ε2M2和εK1+ε2K2分別代表兩者的變化,且當dεM1+ε2M2→0和εK1+ε2K2→0時,M→M0,K→K0;εM1和ε2M2分別為質量矩陣的一次增量和二次增量;εK1和ε2K2分別為剛度矩陣的一次增量和二次增量。
假設原結構的特征值λ0i是特征方程的單根的情形,其相應的特征向量為u0i,它們滿足式(1)。根據攝動理論,將修改后結構的特征值λi和特征向量ui按小參數ε展開為冪級數,即

(4)
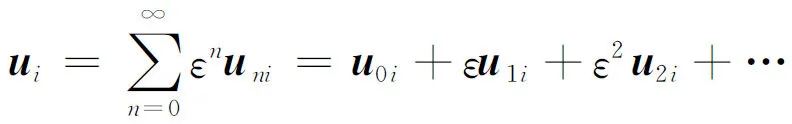
(5)
將式(2)~式(5)代入式(1),并令方程兩端ε的同次冪的系數相等,得
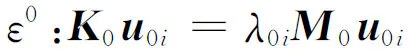
(6)

(7)

(8)
特征向量ui應滿足正則化條件
(9)
將式(2)和式(5)代入式(9),得
(10)
(11)
(12)
(13)
1.1 混合基的構造
假設修改前結構的已知模態個數為q,它們不一定是相鄰的q個低階模態,記為u01,u02,…,u0q,相應的特征值分別為λ01,λ02,…,λ0q,并假設這q個已知模態關于結構修改前的剛度矩陣K0和質量矩陣M0是正交歸一的。
將q個已知模態按行排成一個q×N的矩陣,記為A,即
(14)
矩陣A是行滿秩,記為
(15)
由于M0是實對稱正定的,從而q×N階矩陣B也是行滿秩的。將矩陣B寫為如下分塊形式
(16)
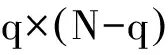
求解下列矩陣方程
(17)
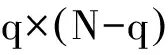
按分塊乘法,由式(17)可得
(18)

(19)
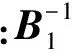


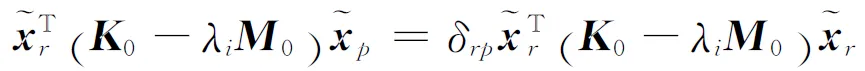
(20)
其中:r=q+1,q+2,…,N;p=q+1,q+2,…,N;δrp為Kronecker符號函數。
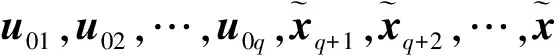
1.2 1階攝動量的混合基展開法
將特征向量的1階攝動量u1i關于混合基展開
(21)
將式(21)代入式(7),得
(22)
(23)
當j=i時,從式(23)可解得關于特征值λi的1階攝動量

(24)
當j≠i時,從式(23)可解得式(21)中系數bij為
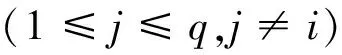
(25)
將式(21)代入式(12),可得
(26)
(27)
其中:i=1,2,…,q;j=q+1,q+2,…,N。
1.3 2階攝動量的混合基展開法
將特征向量的2階攝動量u2i關于混合基展開
(28)
將式(28)代入式(8),得
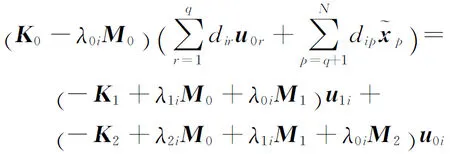
(29)
(30)
當j=i時,從式(30)可解得關于特征值λi的2階攝動量
(31)
當j≠i時,從式(30)可解得式中系數dij
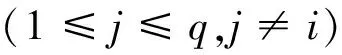
(32)
將式(28)代入式(13),可得
(33)
(34)
其中:i=1,2,…,q;j=q+1,q+2,…,N。
從式(4)、式(24)和式(31)可以看出,結構修改后特征值λi的2階攝動解只與修改前相應特征向量u0i有關。從式(5)、式(21)和式(28)可以看出,結構修改后特征向量ui的1階攝動解和2階攝動解都與修改前模態空間全部基向量相關。
2 算例分析
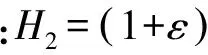
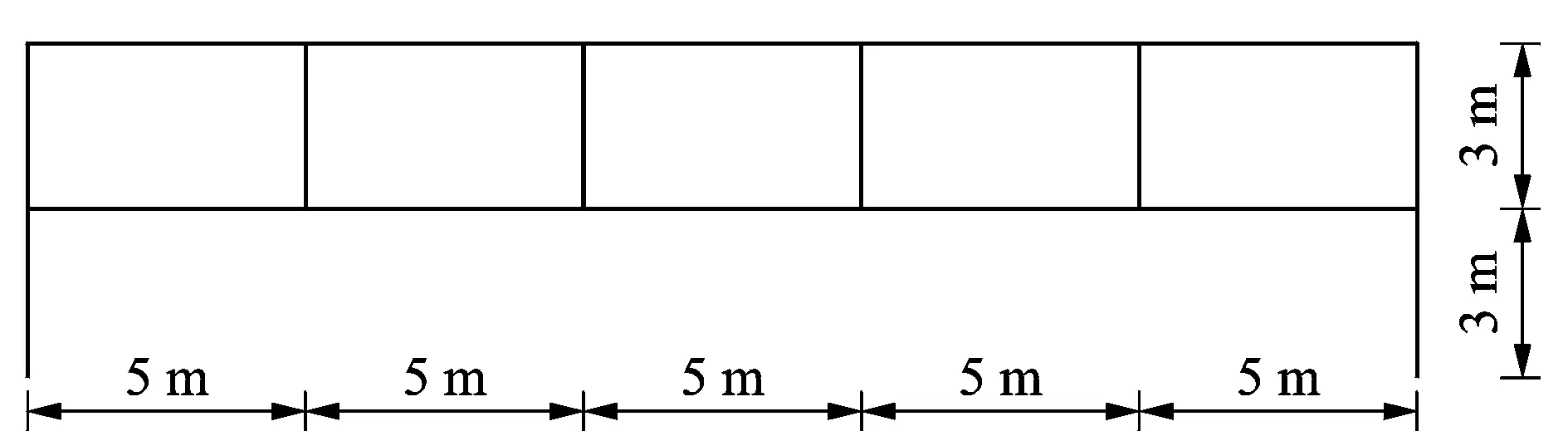
圖1 平面框架結構Fig.1 Plane frame structure
取如下的誤差模來比較文獻[1]和本研究方法關于特征向量的重分析精度

(35)
其中:整數I=1,2,分別對應于文獻[1]和本研究方法;uEk表示修改后結構的第k個精確特征向量;uIk表示由第I種方法計算的結構修改后第k個特征向量的近似值。
從表1中的數值結果可以看出:無論結構參數改變多少,本研究方法計算精度全部高于經典攝動法;隨著結構參數改變增大,兩種方法計算誤差均有所增大;經典2階攝動法在結構參數改變量超過30%以后,計算結果誤差急劇增大,而本研究方法在結構參數改變60%時計算得到的前3階固有頻率的最大誤差也未超過4.0%。因此,本研究方法的適用范圍更廣,適用于結構大修改情況。
3 結束語
筆者針對結構修改和模型校正中存在的模態空間不完備的問題,從線性空間的角度出發,利用已知的少數幾個可能不連續的低階模態構造出整個模態空間的一個混合基,同時將反映結構參數改變的質量矩陣和剛度矩陣的增量表示為高次增量形式,不但保留了經典攝動法簡單易行的特點,還提高了攝動解的精度并擴大了適用范圍,能夠用來解決工程結構大修改情況下的近似重分析問題。

表1 固有頻率和振型向量誤差比較
[1] Chen Suhuan. Matrix perturbation theory in structural dynamic designs[M]. Beijing: Science Press, 2007:36-65.
[2] 張美艷, 韓平疇. 基于有理逼近和靈敏度分析的結構動力重分析方法[J]. 振動與沖擊, 2006, 25(4): 50-52.
Zhang Meiyan, Han Pingchou. Novel method for structural dynamic reanalysis based on rational approximation and eigen-sensitivity[J]. Journal of Vibration and Shock, 2006, 25(4):50-52. (in Chinese)
[3] Yang Xiaowei, Chen Suhuan, Wu Baisheng. Eigenvalue reanalysis of structures using perturbations and padé approximation[J]. Mechanical Systems and Signal Processing, 2001, 15(2): 257-263.
[4] Wu Baisheng, Li Zhengguang, Li Shunhua. The implementation of a vector-valued rational approximate method in structural reanalysis problems[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(13-14): 1773-1784.
[5] Hurtado J E. Reanalysis of linear and nonlinear structures using iterated Shanks transformation[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(37-38): 4215-4229.
[6] Chen Suhuan, Wu Xiaoming, Yang Zhijun. Eigensolution reanalysis of modified structures using epsilon-algorithm[J]. International Journal for Numerical Methods in Engineering, 2006, 66(13): 2115-2130.
[7] Chen Suhuan, Ma Liang, Meng Guangwei. Dynamic response reanalysis for modified structures under arbitrary excitation using epsilon-algorithm[J]. Computers & Structures, 2008, 86(23-24): 2095-2101.
[8] 何建軍, 姜節勝. 基于降階模型的非經典阻尼結構拓撲修改的復模態重分析方法[J]. 振動與沖擊, 2009,28(7): 50-54.
He Jianjun, Jiang Jiesheng. Complex modal reanalysis method for topological modification of a non-classical damped structure based on a reduced model[J]. Journal of Vibration and Shock, 2009, 28(7):50-54. (in Chinese)
[9] Kirsch U. Reanalysis and sensitivity reanalysis by combined approximations[J]. Structural and Multidisciplinary Optimization, 2010, 40(1): 1-15.
[10]Kirsch U, Bogomolni M. Nonlinear and dynamic structural analysis using combined approximations[J]. Computers & Structures, 2007, 85(10): 566-578.
[11]Amir O, Kirsch U, Sheinman I. Efficient non-linear reanalysis of skeletal structures using combined approximations[J]. International Journal for Numerical Methods in Engineering, 2008, 73(9): 1328-1346.
[12]Ma Liang, Chen Suhuan, Meng Guangwei. Combined approximation for reanalysis of complex eigenvalues[J]. Computers & Structures, 2009, 87(7-8): 502-506.
[13]Xu Tao, Guo Guikai, Zhang Hao. Vibration reanalysis using frequency-shift combined approximations[J]. Structural and Multidisciplinary Optimization, 2011,44(2): 235-246.
[14]黃冀卓, 王湛. 大型結構大修改下的靜力重分析方法[J]. 力學學報, 2011, 43(2): 355-361.
Huang Jizhuo, Wang Zhan. Static reanalysis methods for large-scale structures with large modifications[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(2):355-361. (in Chinese)
[15]Han Wanzhi, Song Datong, Chen Suhuan. Mixed-basis superposition method for the perturbation analysis of eigensolutions[J]. Communications in Numerical Methods in Engineering, 1996, 12:835-847.

10.16450/j.cnki.issn.1004-6801.2015.03.026
*國家重點基礎研究發展計劃(“九七三”計劃)資助項目(2010CB736104)
2013-04-09;
2013-05-25
O302
劉志軍,男,1976年4月生,副教授。主要研究方向為結構動力學分析與優化設計、汽車振動分析。曾發表《超長斜拉索張力振動測量的傳遞矩陣法》(《振動、測試與診斷》2012年第32卷第4期)等論文。 E-mail:uliuzj@163.com

