蒙特卡羅方法及其方差縮減技術比較分析

王立雪， 孫聚波， 徐平峰

（長春工業(yè)大學 基礎科學學院，吉林 長春 130012）

0 引 言

蒙特卡羅方法起源于法國數(shù)學家布豐用投針實驗的方法求圓周率π。20世紀40年代馮·諾依曼與S.M.烏拉姆做出了奠基性的工作，他們建立了概率密度函數(shù)、逆累積分布函數(shù)的數(shù)學基礎。時至今天，眾多學者對蒙特卡羅方法已作出了許多改進。這些方法都有其優(yōu)缺點和適用范圍，例如：對偶抽樣在對偶變量和原始變量強負相關時表現(xiàn)很好；控制變量法的改進程度依賴于控制變量與待估變量的相關性；重要性抽樣除了可以改進估計之外，另一個特點是當遇到不易抽樣的分布時，可重新選擇常見的、容易抽樣的分布，但是如果選擇的重要性函數(shù)不適當時，不僅不會減小方差，反而會大大增大方差。

蒙特卡羅方法的計算相對簡單，即使所要解決的問題復雜度很高，也不會影響它的計算精度和收斂速度，而且所需存儲的單元也很少，這些都是用該方法處理大型復雜問題時的優(yōu)勢。蒙特卡羅方法不僅較好地解決了多重積分計算［1］、微積分方程求解［2］、統(tǒng)計特征值計算［3］和非線性方程求解［4］等數(shù)值計算問題，而且廣泛應用于金融工程學［5］、計 量 經(jīng) 濟 學［6－7］、生 物 醫(yī) 學［8］、統(tǒng) 計 物 理學［9］等領域。

1 蒙特卡羅方法的基本原理及其計算精度

在數(shù)理統(tǒng)計中，很多感興趣的量可以表示為某隨機變量h（X）的期望，X的密度為f（x），則

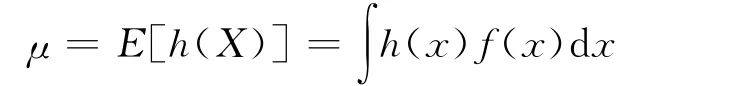
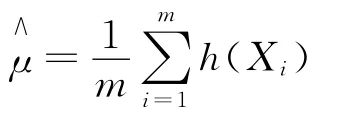
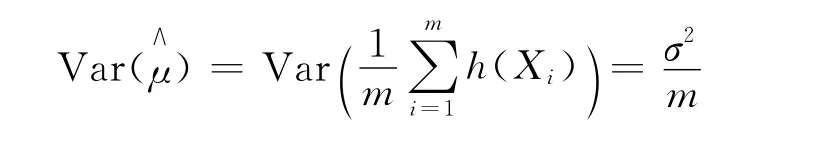
由中心極限定理知，當m足夠大時

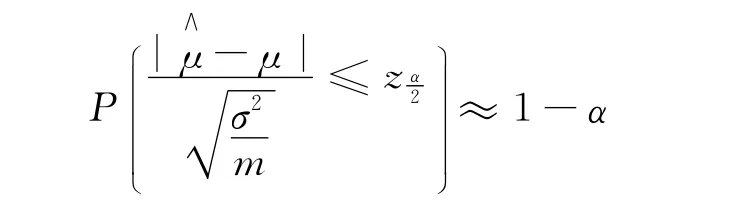
蒙特卡羅方法的估計μ∧與期望μ的誤差為：

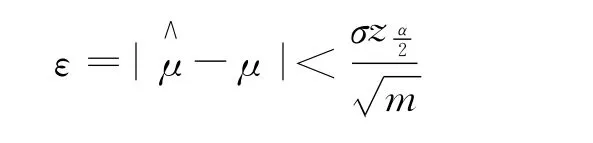
2 方差縮減技術

目前，常見的方差縮減技術有分層抽樣法［10］、重 要 性 抽 樣 法［11］、條 件 期 望 法［12－13］、對 偶變量法［10，14］、控 制 變 量 法［15］等，以 及 混 合 運 用 他們的技術。綜合考慮技術的適用性和流行性，文中先簡要介紹原始權重的重要性抽樣法、標準化權重的重要性抽樣法、對偶變量法、控制變量法，而后進行模擬研究。

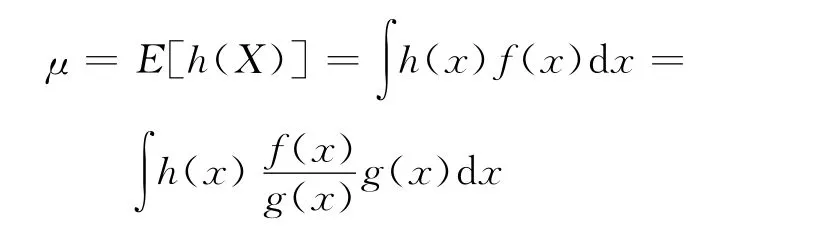
從g（x）中抽取i.i.d樣本X1，X2，…，Xm，則μ的估計為：

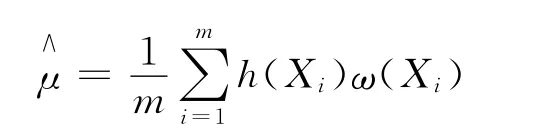
2.1 重要性抽樣法

重要性抽樣法通過改變現(xiàn)有樣本空間的概率分布，提高“重要”區(qū)域的抽樣權重，使對最后結果貢獻大的樣本出現(xiàn)的概率變大，以便減少方差，提高估計精度。

原始權重的重要性抽樣原理：選取與f（x）有相同支撐集的另一個密度函數(shù)g（x），這里稱其為重要性函數(shù)或包絡函數(shù)。則期望可表示為：

標準權重的重要性抽樣原理：在標準權重的重要性抽樣中，期望可表示為：

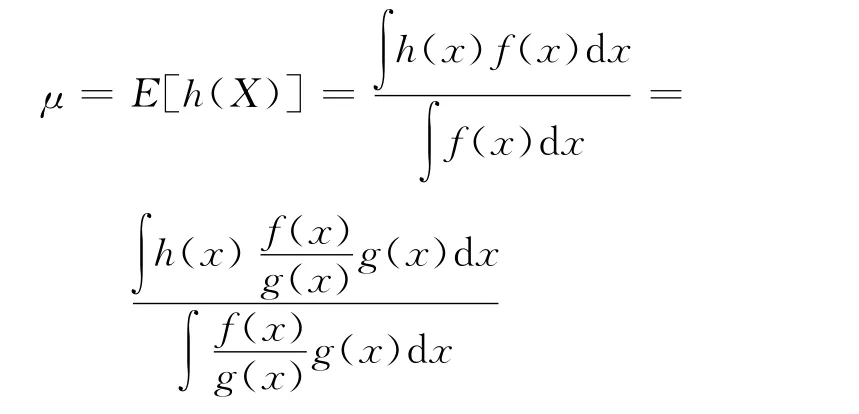
從g（x）中抽取i.i.d樣本X1，X2，…，Xm，則μ的估計為：

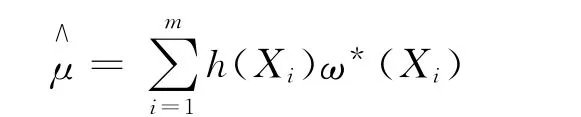
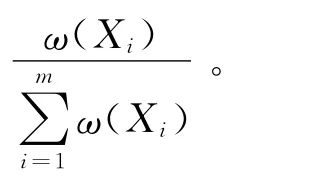
原始權重的重要性抽樣步驟如下：

1）選取重要性函數(shù)g（x），從g（x）中抽取i.i.d樣本X1，X2，…，Xm；

標準化權重的重要性抽樣步驟如下：

1）選取重要性函數(shù)g（x），從g（x）中抽取i.i.d樣本X1，X2，…，Xm；

2.2 對偶變量法

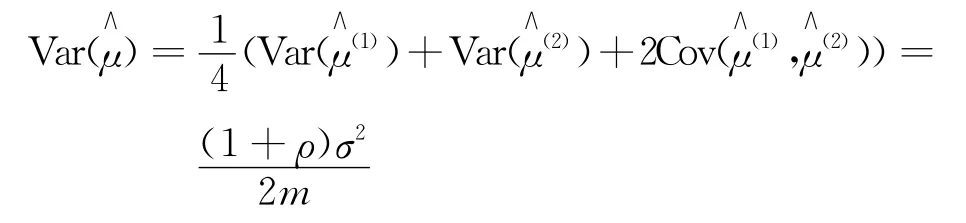
式中：ρ——兩個估計的相關系數(shù)。

對偶變量法步驟如下：

1）從U（0，1）中產(chǎn)生m個隨機數(shù)U1，U2，…，Um；

2）令

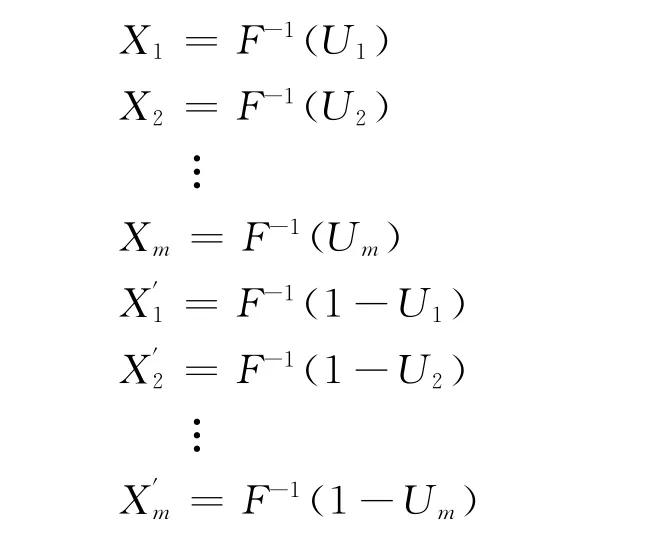
其中，F(xiàn)（X）為隨機變量X的累積函數(shù)；

3）兩個估計分別為：

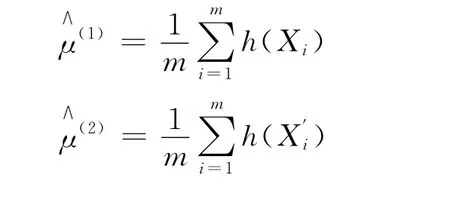
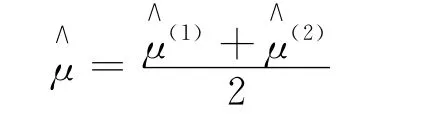
2.3 控制變量法

取與h（X）相關的隨機變量t（X），它的期望已知為θ。θ和μ的簡單蒙特卡羅估計為對常數(shù)c為μ的無偏估計，稱其為控制變量估計，稱t（X）為h（X）的控制變量。的方差為：

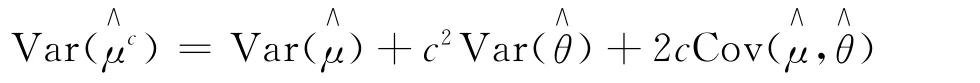
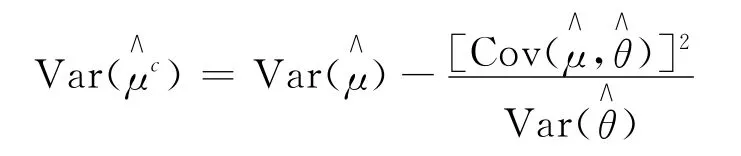
此時

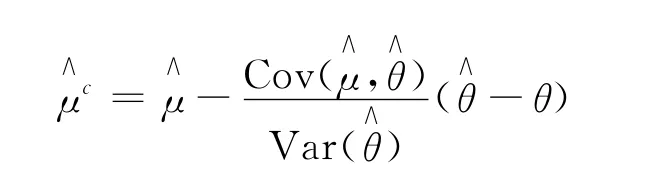
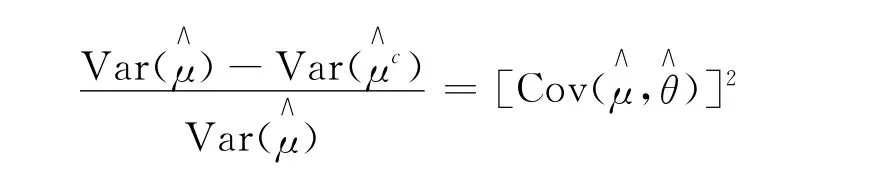
可以看出，控制變量t（X）與h（X）相關性越強，方差縮減率越大。

控制變量法步驟如下：

1）從f（x）中抽取i.i.d樣本X1，X2，…，Xm；

2）選取控制變量t（X），其期望已知為θ，計算：

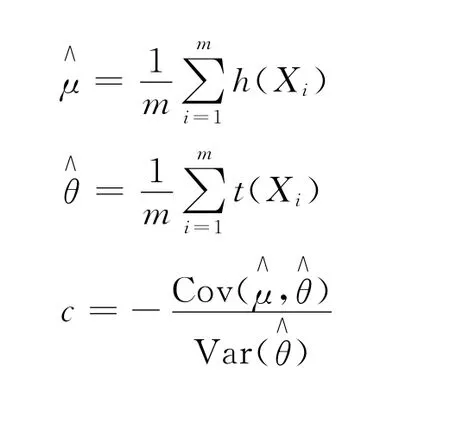
3 模擬研究

下面分別從數(shù)值分析和統(tǒng)計推斷方面設計問題，通過模擬比較這幾種方法的表現(xiàn)。問題1：求積分的估計值。被積函數(shù)在［0，1］上單調(diào)。我們選取的重要性函數(shù)，控制變量t（X）＝e－x都與h（X）比較接近。

問題1的模擬結果見表1。

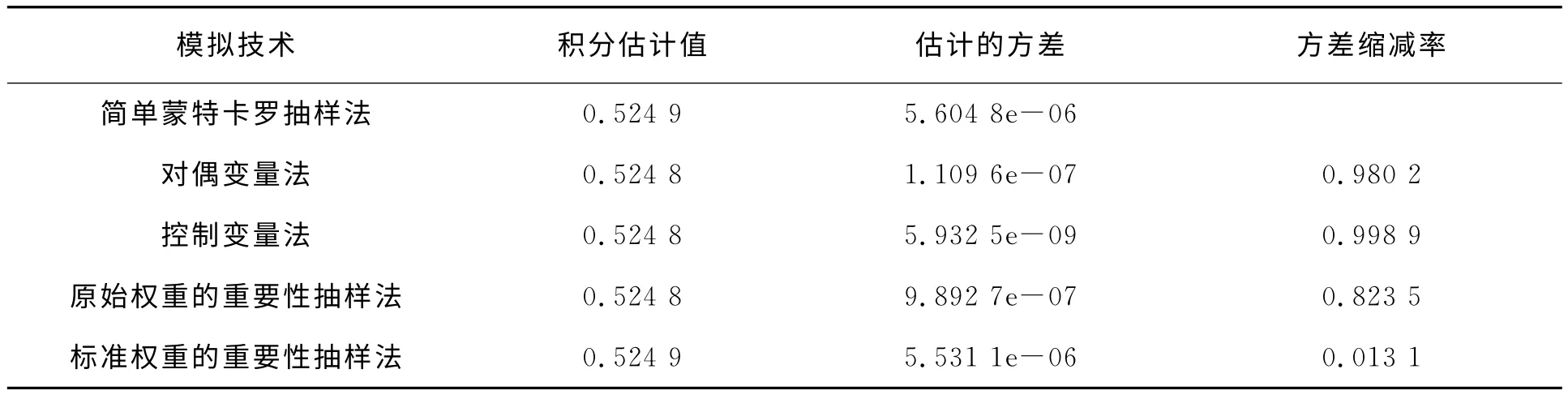
表1 問題1的模擬結果

從表1可以看出，幾種方差縮減技術得到的積分估計值比較相近，沒有明顯差異。其中，由各技術的方差縮減率可知，原始權重的重要性抽樣、控制變量法和對偶變量法的表現(xiàn)都很好，這依賴于模擬中取的重要性函數(shù)、對偶變量以及控制變量與原始變量的相關性都很強。

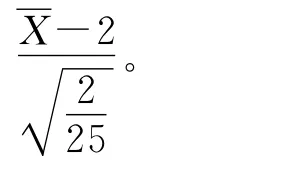
1）使用5種蒙特卡羅方法：簡單蒙特卡羅抽樣、對偶變量法、原始權重和標準化權重的重要性抽樣，以及帶控制變量的重要性抽樣［16］，估計該檢驗的I型錯誤率。討論每種方差縮減技術的表現(xiàn)。

2）對λ∈［2.2，4］，用同樣的5種技術畫出該檢驗的功效曲線。給出每種情況下的逐點置信區(qū)間。

在各種重要性抽樣中，皆取λ＝2.465 3的Possion分布為重要性函數(shù)；在用控制變量改進的重要性抽樣中，控制變量取為權重函數(shù)的樣本均值

問題2中1）的模擬結果見表2。

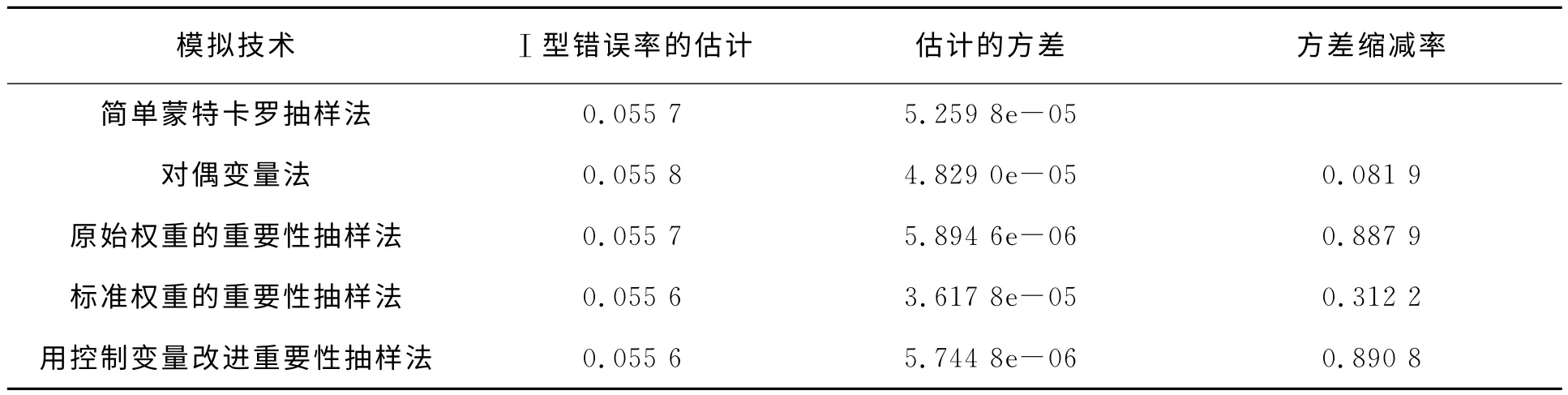
表2 問題2中1）的模擬結果

從表2可以看出，幾種方差縮減技術得到的 Ⅰ型錯誤率的估計值都在0.055～0.056之間，沒有明顯的差異。其中，對偶變量法中的方差縮減率僅為0.081 9，對計算精度改進程度不大。同時也看到重要性抽樣的方差縮減率為0.887 9，對計算精度的改進很大；相對地，標準化權重的重要性抽樣的方差縮減率僅為0.312 2，結合表1可知，標準化權重未必能改進重要性抽樣。最后，采用控制變量改進的重要性抽樣法的方差縮減率為0.890 8，改進精度最好。

下面給出問題2中2）用5種技術畫出的功效曲線和逐點置信區(qū)間，直觀地顯示了這幾種方法的表現(xiàn)，分別如圖1～圖5所示。

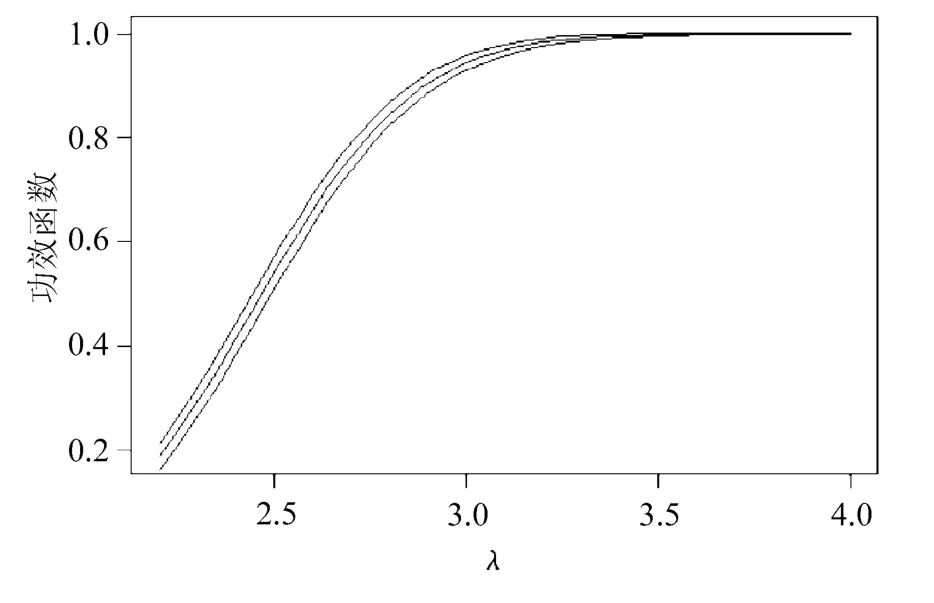
圖1 簡單蒙特卡羅抽樣的功效及置信區(qū)間

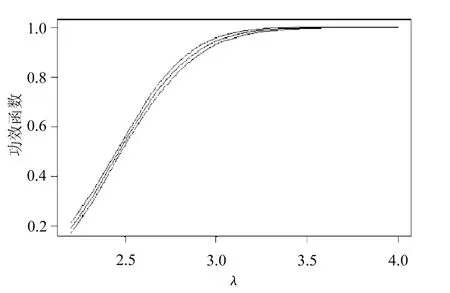
圖2 對偶變量法的功效及置信區(qū)間

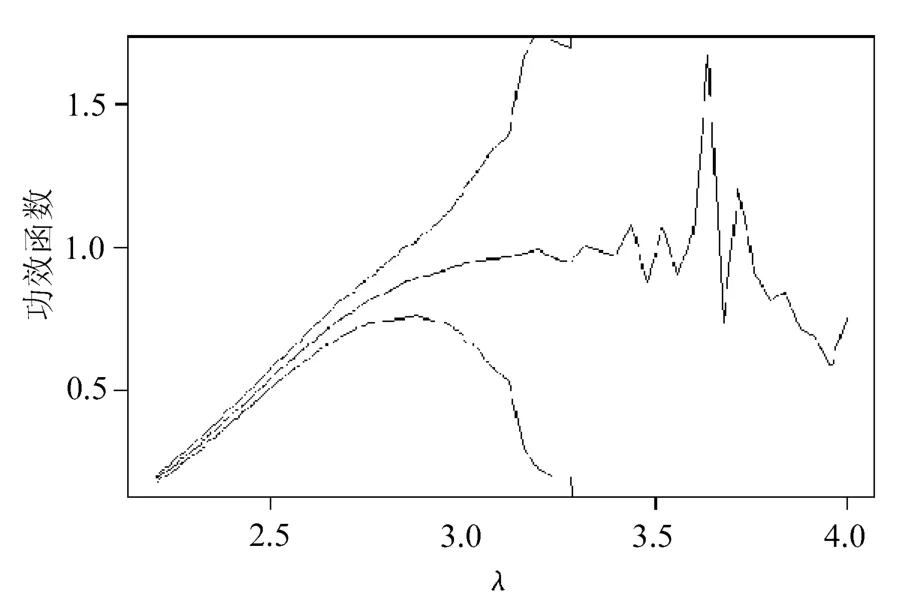
圖3 原始權重的重要抽樣的功效及置信區(qū)間

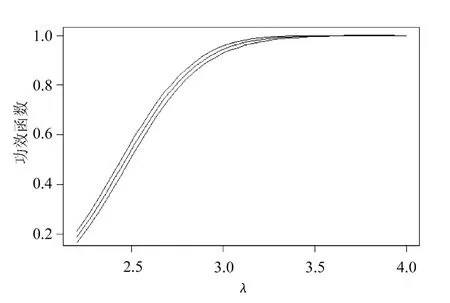
圖4 標準權重的重要抽樣的功效及置信區(qū)間

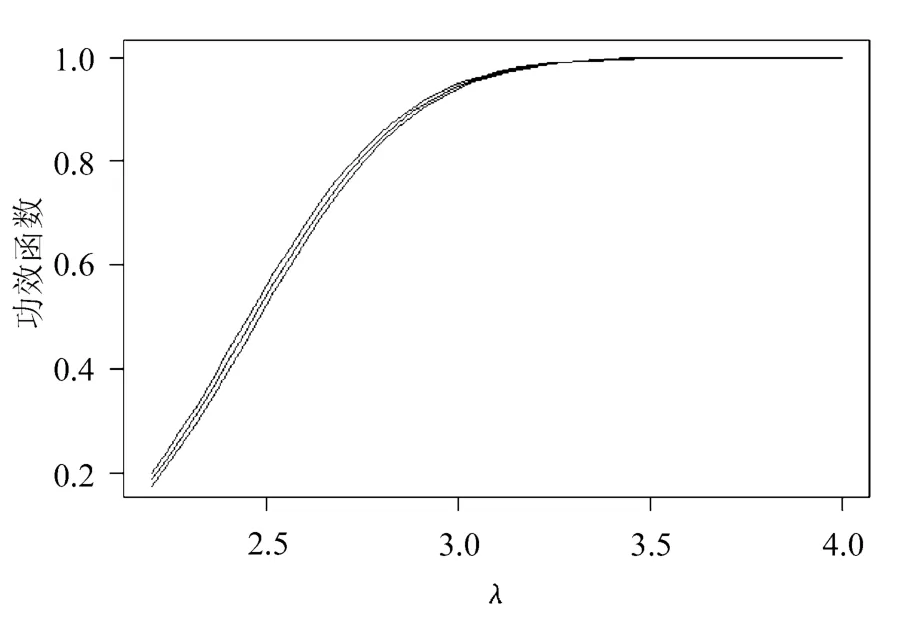
圖5 帶控制變量的重要性抽樣的功效及置信區(qū)間

從圖2、圖4與圖1的比較中可以看出，對偶變量法、標準權重的重要性抽樣二者無論是在待估功效很小還是很大時都有改進，表現(xiàn)相對穩(wěn)定。再觀察圖3可知，原始權重的重要性抽樣在估計功效很小時方差非常小，估計精度很好，但隨著估計功效的增大，估計越來越不穩(wěn)定，以至讓人無法接受的程度，這恰恰反映了原始權重的重要性抽樣更適合估計小概率問題。通過圖1～圖5的比較可知，帶控制變量的重要性抽樣表現(xiàn)是5種技術中最好的，它對重要性抽樣改進很大。

4 結 語

綜合理論知識和模擬結果，蒙特卡羅方法及其改進方法利用產(chǎn)生的大量隨機樣本來估計問題，簡單易行。文中列舉的方差縮減技術都有其特點和適用范圍，若將各種技術結合使用，可以有效地減小方差，提高計算精度。

［1］ 同濟大學計算數(shù)學教研室.現(xiàn)代數(shù)值計算［M］.北京：人民郵電出版社，2009.

［2］ 洪志敏.基于Monte－Carlo技術的積分（微分）方程數(shù)值求解方法研究［D］.呼和浩特：內(nèi)蒙古工業(yè)大學，2013.

［3］ 王克沖.用蒙特卡洛法求多維隨機變量函數(shù)的統(tǒng)計特征值［J］.南京理工大學學報：自然科學版，1986（1）：77－81.

［4］ 王克，薛小超，朱朋海.非線性方程的多核并行蒙特卡洛求解方法［J］.現(xiàn)代計算機：中旬刊，2014（7）：38－44.

［5］ P Glasserman.金融工程中的蒙特卡羅方法［M］.范韶華，孫武軍，譯.北京：高等教育出版社，2013.

［6］ D N Gujarati，D C Porter.計量經(jīng)濟學基礎［M］.費劍平，譯.5版.北京：中國人民大學出版社，2011.

［7］ 董小剛，王淑影，王純杰.基于動態(tài)因子的經(jīng)濟水平差異分析［J］.長春工業(yè)大學學報，2015，36（2）：125－129.

［8］ 任曉楠，魏守水，楊憲章，等.光能量在生物組織中傳輸?shù)拿商乜_研究［J］.生物醫(yī)學工程學雜志，2010（3）：652－657.

［9］ K Binder，D W Heermann.Monte carlo simulation in statistical physics［M］.5th edition.北京：世界圖書出版公司，2014.

［10］ S M Ross.Simulation［M］.2nd edition.San Diego，CA：Academic Press，1997.

［11］ G H Givens，J A Hoeting.Computational statistics［M］.Wiley：［s.n.］，2005.

［12］ G Casella，C Robert.Rao－Blackwellization of sampling schemes［J］.Biometrika，1996，83：81－94.

［13］ A Gelfand，A F M Smith.Sampling based approaches to calculating marginal densities［J］.Journal of the American Statistical Association，1990，85：398－409.

［14］ J M Hammersley，K W Morton.A new monte carlo technique：antithetic variates［J］.Mathematical Proceedings of the Cambridge Philosophical Society，1956，52：449－475.

［15］ J S Liu.Monte carlo strategies in scientific computing［M］.New York：Springer－Verlag，2001.

［16］ T Hsterberg.Weighted average importance sampling and defensive mixture distributions［J］.Technometrics，1995，37：185－194.