一類非線性脈沖拋物型系統在Robin邊值條件下的振動性
劉俊紅, 鄭素文, 李立峰, 金 琦
(裝甲兵工程學院基礎部,北京 100072)
一類非線性脈沖拋物型系統在Robin邊值條件下的振動性
劉俊紅, 鄭素文, 李立峰, 金 琦
(裝甲兵工程學院基礎部,北京 100072)
討論了一類含脈沖的非線性拋物型方程組非零解的振動性,利用Green定理及Jensen不等式,得出了該系統在Robin邊界條件下非零解振動的若干準則。
非線性;脈沖;拋物型系統;振動性
近十幾年來,非線性脈沖控制偏微分系統問題受到了學者的廣泛關注,其中振動性也隨之成為研究的熱點之一。傅希林等[1]、Deng等[2]分別研究了相關脈沖拋物系統在2類邊界條件下解的振動準則。另外,Drumi等[3]研究了一類脈沖拋物方程解的振動準則,文獻[4-5]作者研究了脈沖時滯拋物方程解的振動條件,得出了相關結論。
本文在文獻[1-2]的基礎上,開展2方面的研究工作:1) 將系統進行改進,并對其非線性項放寬了條件,改進的系統為
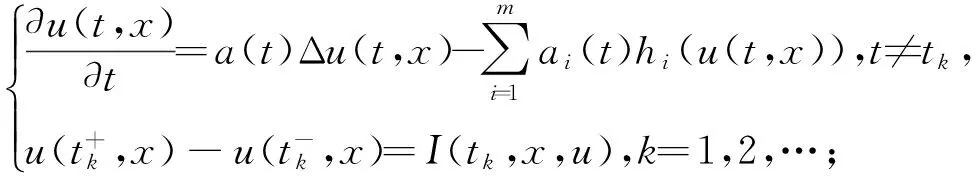
(1)
2) 研究該系統在Robin邊值條件
(2)
1 基本假設
對于上述邊值問題,本文作如下假設。

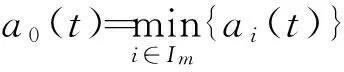
I(tk,x,-u(tk,x))=-I(tk,x,u(tk,x)),k=1,2,…;且∫ΩI(tk,x,u(tk,x))dx≤αk∫Ωu(tk,x)dx,k=1,2,…,其中αk>0,為常數。

定義1: 若下列條件成立,則稱u(t,x)為邊值問題(1)、(2)的解。
1)u(t,x)關于t一階可微,關于x二階可微,t≠tk,k∈I∞,I∞={1,2,…};
2)u(t,x)在t=tk(k∈I∞)處為關于t的第1類間斷點的光滑連續函數,且H3成立;
3)u(t,x)在區域G內滿足式(1)、(2)。
定義2: 設u(t,x)為邊值問題(1)、(2)的1個非零解,若存在T>0,使得當(t,x)∈[T,+∞)×Ω時,u(t,x)恒正或恒負,則稱u(t,x)在區域G內是非振動的;否則,是振動的。
2 主要結論
引理1[6]: 假設λ1為特征值問題
(3)
的最小特征值,Φ1(x)為對應的特征函數,且β(x)∈C(?Ω,(0,+∞)),則λ1>0,Φ1(x)>0。令
F1(t)=∫?Ωφ1(t,s)Φ1(s)ds,
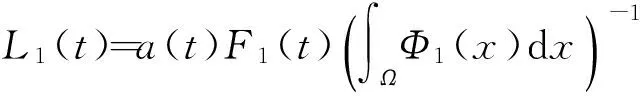
定理1: 假設條件H1,…,H4成立,若脈沖微分不等式
(4)
和
(5)
無最終正解,則邊值問題(1)、(2)的所有非零解在區域G內是振動的。
證明: 應用反證法進行證明。設u(t,x)為邊值問題(1)、(2)的1個非零解,且存在T>0,使得當(t,x)∈[T,+∞)×Ω時,u(t,x)不變號,不妨設u(t,x)>0。
當t≠tk時,在式(1)兩端乘以式(3)的特征函數Φ1(x),并對x在Ω上進行積分,則
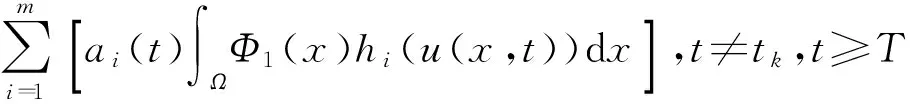
(6)
利用Green定理,結合式(2)、(3),有
∫ΩΦ1(x)Δu(t,x)dx=
∫?Ωφ1(t,s)Φ1(s)ds-λ1∫ΩΦ1(x)u(t,x)dx=
F1(t)-λ1∫ΩΦ1(x)u(t,x)dx,t≠tk,t≥T。
(7)
利用Jensen不等式,結合假設H2,有
t≠tk,t≥T。
結合假設H4,進一步有
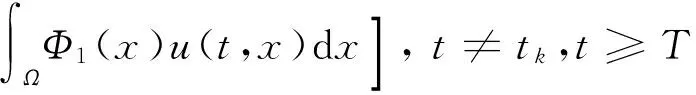
(8)
結合式(6)-(8),有
∫ΩΦ1(x)u(t,x)dx-a0(t)∫ΩΦ1(x)dx×
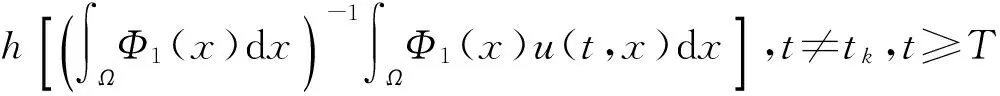
(9)
令

(10)
可得
t≠tk,t≥T。
(11)
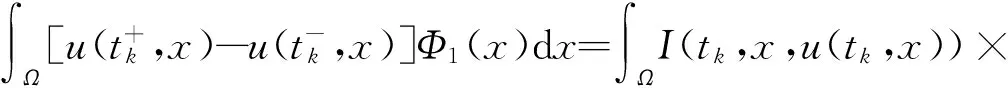
Φ1(x)dx≤αk∫Ωu(tk,x)Φ1(x)dx,k=1,2,…。
于是有
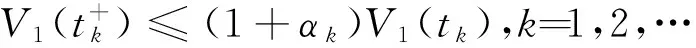
(12)
由式(11)、(12)可知:V1(t)是脈沖微分不等式(4)的1個最終正解,這與定理1的條件相矛盾。所以,u(t,x)在區域G內是振動的。
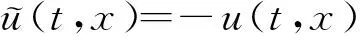
是式(5)的一個最終正解,這與定理1的條件相矛盾。所以,u(t,x)在區域G內是振動的。
證畢。
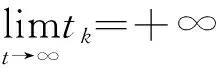
定理2: 假設H1,…,H4成立,且

(13)
若對于充分大的T>0,有
(14)
和
(15)
成立,則邊值問題(1)、(2)的所有非零解在區域G內是振動的。
證明: 由定理1可知,只需證明脈沖微分不等式(4)、(5)無最終正解即可。
令V1(t)為脈沖微分不等式(4)的一個最終正解,則存在T>0,使得當t≥T時,V1(t)>0,且f(V1(t))>0。于是,
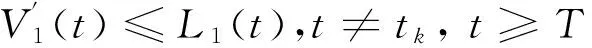
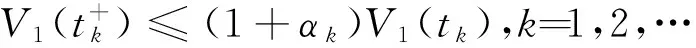
由引理2可得
L1(s)ds,t≥T。
(16)
進一步可得
L1(s)ds,t≥T。
(17)
令t→+∞,并考慮式(14),可得

(18)

利用式(15)也可以推出脈沖微分不等式(5)無最終正解。
證畢。
[1] 傅希林, 閆寶強, 劉衍勝, 脈沖微分系統引論[M].北京:科學出版社,2005,273-278.
[2] Deng L H, Tan Y M, Yu Y H.Osillation Criteria of Solutions for a Class of Impulsive Parabolic Differential Equation [J]. India J Pure Appl Math,2002, 33(7):1147-1153.
[3] Drumi B, Emil M.Oscillation of the Solutions of Impulsive Parabolic Equations[J]. Journal of Computational and Applied Mathematics,1996,69(2):207-214.
[4] Fu X L, LieJune S. Oscillation Criteria for Impulsive Parabolic Boundary Value Problem with Delay[J]. Applied Mathematics and Computation,2004,153(2):587-599.
[5] Han M A, Li W N. Oscillation of Solutions for Certain Impulsive Vector Parabolic Differential Equations with Delays[J]. Journal of Mathematical Analysis and Applications,2007,326(1):363-371.
[6] 葉其孝,李正元.反應擴散方程引論[M].北京:科學出版社,1990:194-195.
[7] Pirapikaran R. Diff Equs Applied by R Aftabizabeh [M]. Ohio State: Ohio University Press, 1989: 296-308.
(責任編輯: 王生鳳)
Oscillation Criteria for a Class of Nonlinear Impulsive Parabolic System under Robin Boundary Condition
LIU Jun-hong, ZHENG Su-wen, LI Li-feng, JIN Qi
(Department of Fundamental Courses, Academy of Armored Force Engineering, Beijing 100072, China)
In this paper, the authors discuss oscillation of non-zero solutions for a class of nonlinear impulsive parabolic system. Several oscillation criteria are obtained under Robin boundary condition by using the Green formula and Jensen inequality.
nonlinear; impulse; parabolic system; oscillation
1672-1497(2015)03-0108-03
2014-12-23
劉俊紅(1976-),男,講師,博士。
O175.26
A
10.3969/j.issn.1672-1497.2015.03.022

