關(guān)于Sakaguchi函數(shù)類的子類

徐 能，朱慧秋

（1.常熟理工學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，江蘇 常熟 215500；2.常熟市外國(guó)語(yǔ)初級(jí)中學(xué)，江蘇 常熟 215500）

1 引言

全文設(shè)

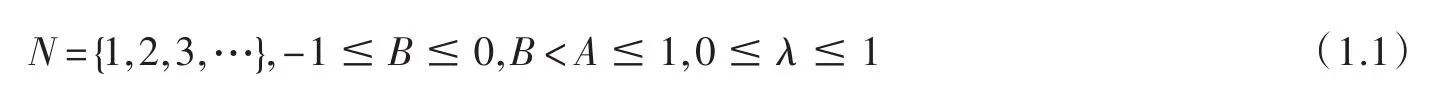
設(shè) f(z),g(z)在單位圓盤U={z:||z＜1}內(nèi)解析，若存在U內(nèi)解析函數(shù)w(z)使|w(z)|≤|z|且f(z)=g(w(z))(z∈U)，稱 f(z)在U內(nèi)從屬于 g(z)，記作 f(z)?g(z)(z∈U).設(shè)A表示U內(nèi)形為

的解析函數(shù)類；S表示A中單葉函數(shù)組成的子類.Sakaguchi[1]引進(jìn)了類

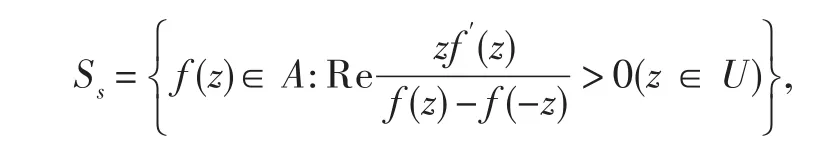
并證得Ss?K(?S)，這里K是U內(nèi)近于凸函數(shù)類.Sakaguchi函數(shù)類Ss也稱關(guān)于對(duì)稱點(diǎn)的星形函數(shù)類.類Ss與各種相關(guān)的函數(shù)類已被許多學(xué)者所研究，例如可參見文獻(xiàn)[1-11].

在我們的研究中需要以下引理.

引理設(shè)（1.2）給出的 f(z)∈A滿足

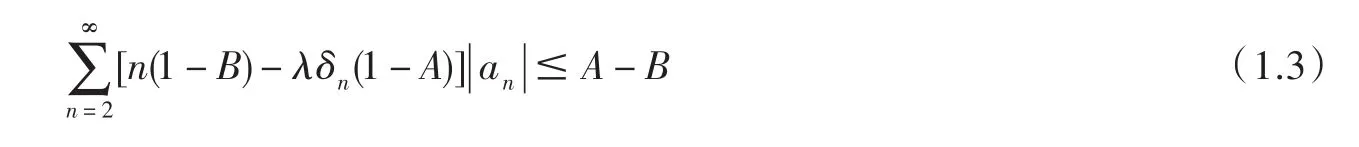
則

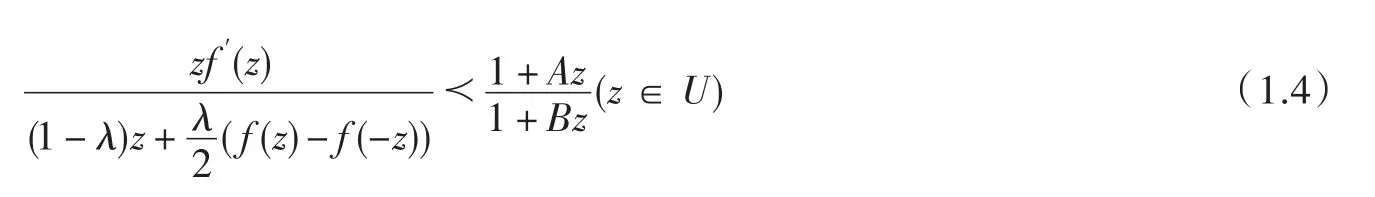
這里

證明由（1.1）和（1.5），Aλδn-nB≥-B(n-λδn)≥0(n≥2). 設(shè)，則有

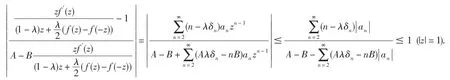
因此，應(yīng)用最大模原理得從屬關(guān)系（1.4）.

我們現(xiàn)在考慮A的以下兩個(gè)子類：

定義1 （1.2）給出的函數(shù) f(z)∈A稱為在類F(λ,A,B)中當(dāng)且僅當(dāng)它滿足系數(shù)不等式（1.3）.

從引理看到，若 f(z)∈ F(λ,A,B)，則從屬關(guān)系（1.4）成立.

定義2（1.2）給出的函數(shù) f(z)∈A稱為在類G(λ,A,B)當(dāng)且僅當(dāng)它滿足系數(shù)不等式

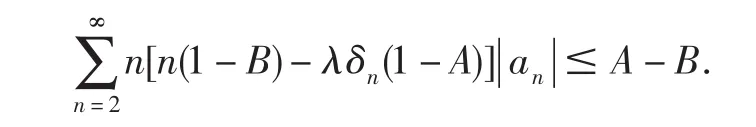
顯然對(duì) f(z)∈ A ，f(z)∈ G(λ,A,B)? zf′(z)∈ F(λ,A,B).

若 我 們 寫 αn=αn(λ,A,B)==nαn>αn(n≥2),則 容 易 驗(yàn) 證

因此有以下包含關(guān)系：若 0≤ λ≤λ0≤1,-1≤ B0≤B＜A≤ A0≤ 1,B≤ 0,則 G(λ,A,B)?F(λ,A,B)?F(λ0,A0,B0)? F(1,1,-1)? SS,G(λ,A,B)? G(λ0,A0,B0)? G(1,1,-1).

這表明 F(λ,A,B)和 G(λ,A,B)都是 Ss的子類. 對(duì)于函數(shù)f1(z)與 f2(z)的 Ha?damard乘積或卷積定義為

本文的目的是討論函數(shù)類F(λ,A,B)和G(λ,A,B)的畸變不等式，包含關(guān)系與卷積性質(zhì).

2 畸變不等式

定理1設(shè)則對(duì) z∈ U 有

（i）

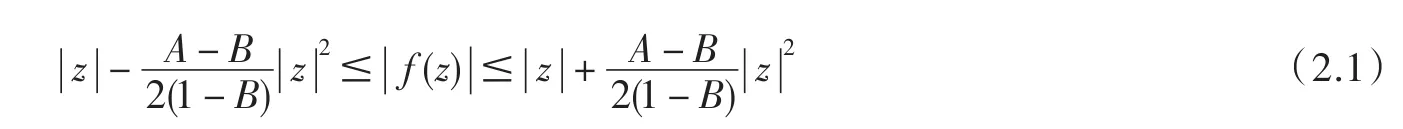
（ii）當(dāng) A=1，

（iii）當(dāng)A＜1，

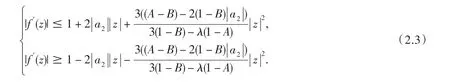
證明（i）對(duì) n=2m(m∈N)有 δn=0，n(1-B)-λδn(1-A)≥2(1-B).

對(duì) n=2m+1(m ∈ N)有 δn=1，n(1-B)- λδn(1-A)≥ 3(1-B)- λ(1-A)≥ 2(1-B).因此

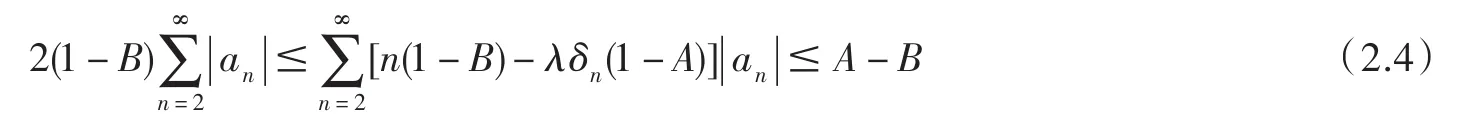
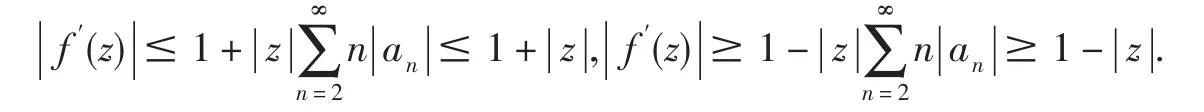
（iii）當(dāng)A＜1，對(duì) n=2m+1(m∈ N)有

對(duì) n=2m(m∈N)有

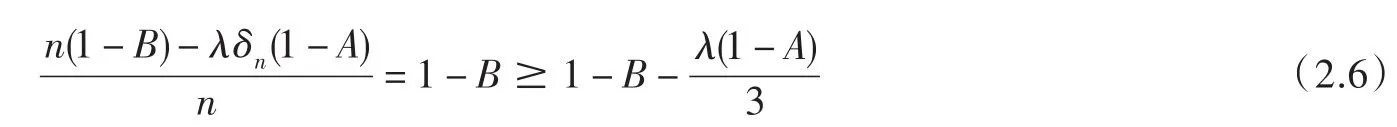
同理可得（2.3）中等二個(gè)不等式.

定理2設(shè) f(z)∈G(λ,A,B)，則對(duì) z∈U 有

（i）

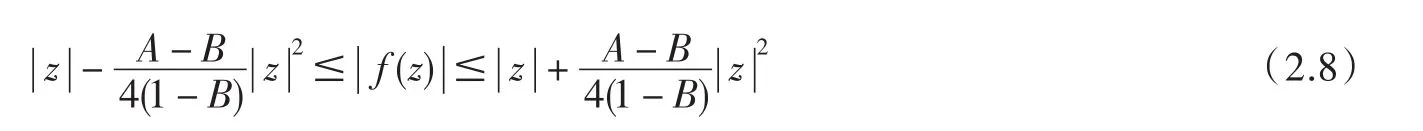
（2.8）中的界是準(zhǔn)確的，有極值函數(shù)

（ii）

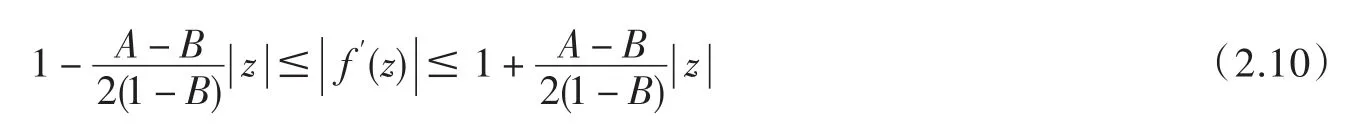
（2.10）中的界是準(zhǔn)確的，有極值函數(shù)（2.9）.證明從略.

3 在G(λ,A,B)與F(λ,C,D)之間的包含關(guān)系

下一定理推廣且改進(jìn)前面提到的包含關(guān)系G(λ,A,B)?F(λ,A,B).

定理3對(duì)于 -1≤D≤0,G(λ,A,B)?F(λ,C(D),D).

證明我們有設(shè) f(z)∈ G(λ,A,B)，易知為證明 f(z)∈ F(λ,C(D),D)，只要找最小的C(D＜C≤1)使

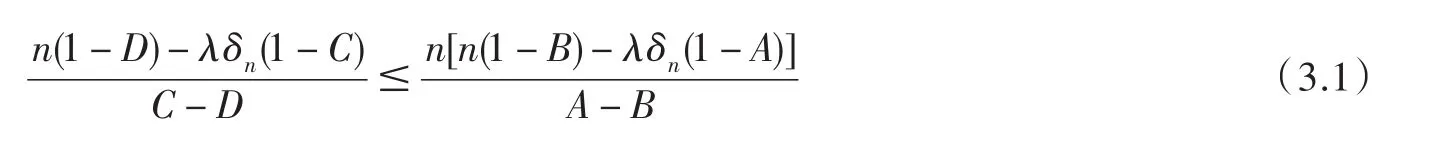
對(duì)一切n≥2成立，或即

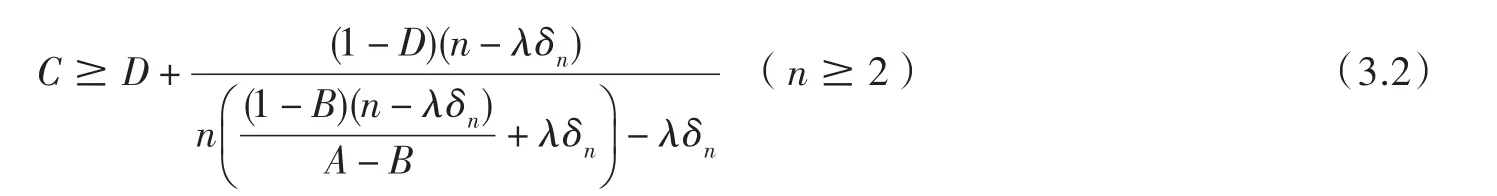
當(dāng) n=2m+1(m∈N)，（3.2）寫成

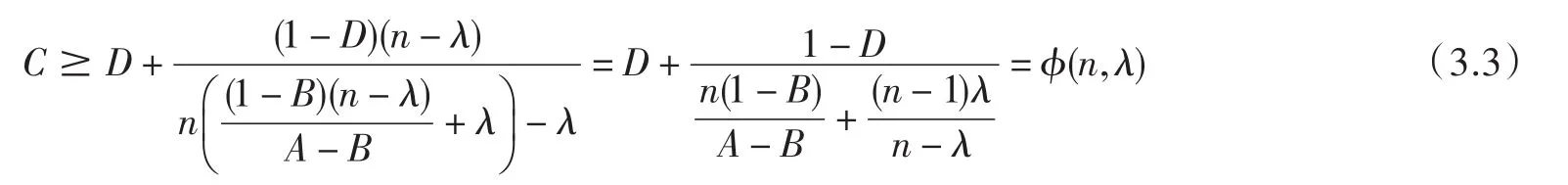
易知 ?(n,λ)(n≥2,0≤ λ≤1)關(guān)于n是遞減的，故

當(dāng) n=2m(m∈N)，（3.2）化為

且有

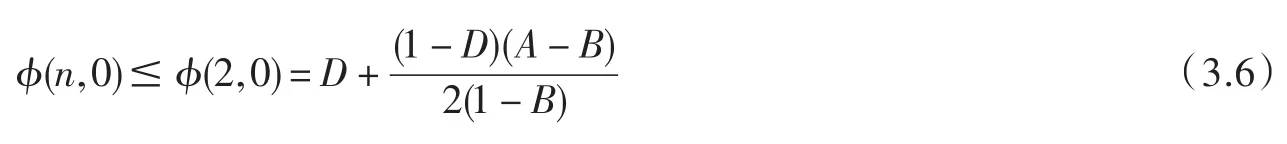
顯然 ?(3,λ)＜?(2,0). 因此，若取 C=?(2,0)=C(D)，則從（3.1）到（3.6）斷定 f(z)∈F(λ,C(D),D).

進(jìn) 而 ，對(duì) D＜C0＜C(D)，有這表明（2.9）定義的函數(shù)

f(z)∈ G(λ,A,B)不在類 F(λ,C0,D)中. 定理證畢.在定理3中取D=B立得下述結(jié)果：

推論1且數(shù)不能再小.

4 卷積性質(zhì)

本節(jié)中設(shè) -1≤ Bj≤ 0,Bj＜Aj≤1(j=1,2).

定理4 設(shè) fj(z)∈ F(λ,Aj,Bj)(j=1,2)，則 (f1*f2)(z)∈ F(λ,A(B),B),這里且數(shù) A（B）不能再小.

證 明首 先設(shè)則

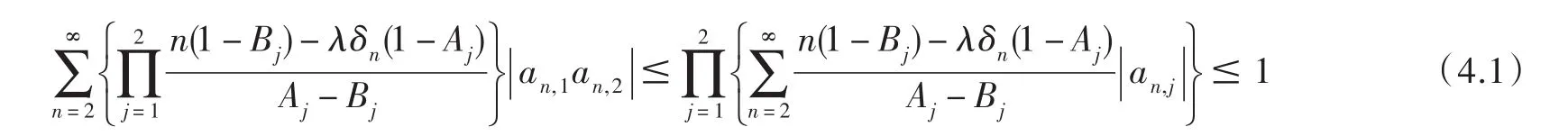
而 (f1*f2)(z)∈ F(λ,A,B)當(dāng)且僅當(dāng)

為證明定理4，從（4.1）和（4.2）知只要找最小的A使對(duì)一切n≥2有

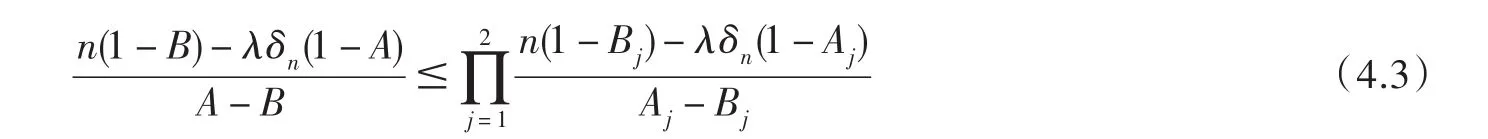
或即

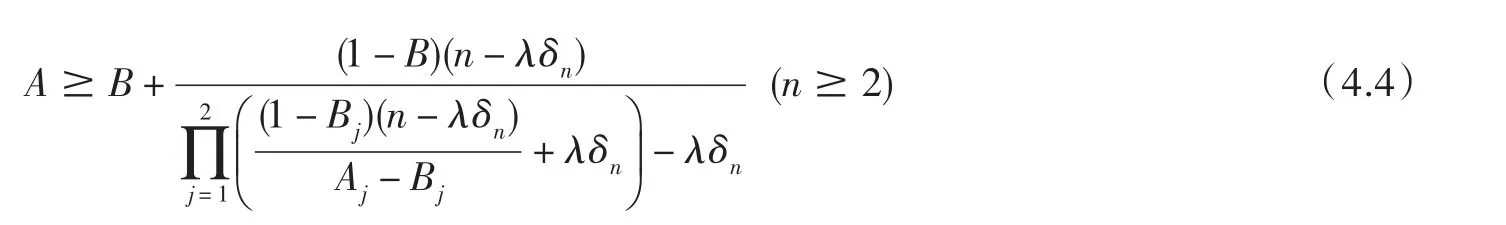
當(dāng) n=2m+1(m∈N)，（4.4）可寫成

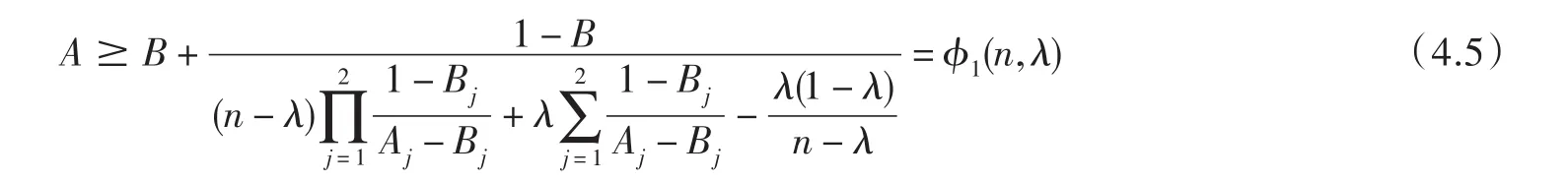
顯然函數(shù) ?1(n,λ)(n≥2,0≤λ≤1)是n的減函數(shù)，故

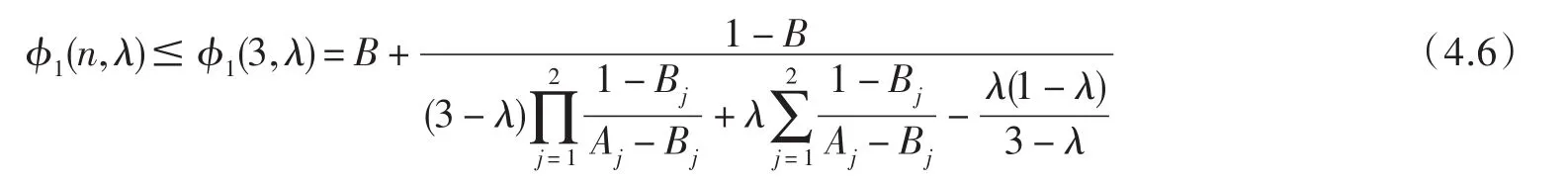
當(dāng) n=2m(m∈N)，（4.4）化為

且有

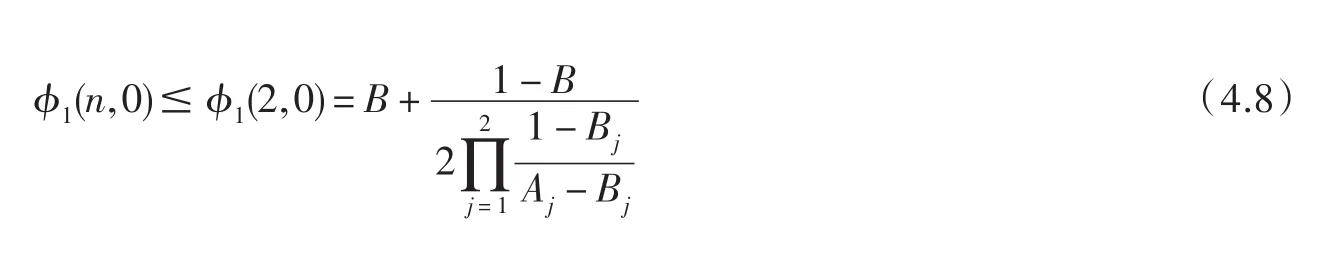
現(xiàn)在

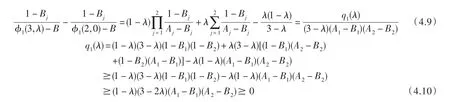
因此，從（4.3）到（4.10）可見 ?1(3,λ)≤ ?1(2,0)=A(B),(f1*f2)(z)∈ F(λ,A(B),B).

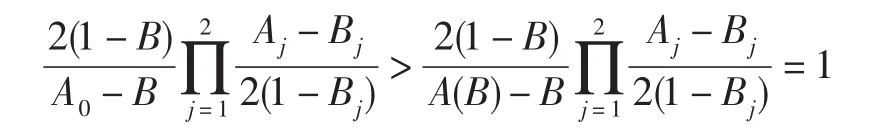
因此 (f1*f2)(z)? F(λ,A0,B). 證畢.

推論2 設(shè) f1(z)∈ F(λ,A1,B1),f2(z)∈ G(λ,A2,B2),則 (f1*f2)(z)∈ G(λ,A(B),B),這里 A（B）與定理 4 中相同，且A（B）不能再小.

定理5 設(shè) f1(z)∈ F(λ,A1,B1),f2(z)∈ G(λ,A2,B2),則 (f1*f2)(z)∈ F(λ,A~1(B),B),

定理6 設(shè) fj(z)∈ G(λ,Aj,Bj)(j=1,2) ，則 (f1*f2)(z)∈ F(λ,2(B),B). 這 里且2(B)不能再小.證明從略.

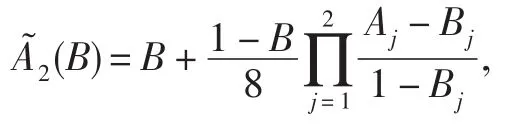
[1]Sakaguchi K.On a certain univalent mapping[J].J Math Soc Japan,1959,11:72-75.

[2]Cho N E,Kwon O S,Owa S.Certain subclasses of Sakaguchi functions[J].Southeast Asian Bull Math,1993,17:121-126.

[3]Owa S,Wu Z,Ren F Y.A note on certain subclass of Sakaguchi functions[J].Bull Soc Rog Sci Liege,1998,57:143-149.

[4]Stankiewicz J.Some remarks on functions starlike with respect to symmetric points[J].Ann Univ Mariae Curie-Sklodowsha Sect A,1965,19:53-59.

[5]Halim S A.Functions starlike with respect to other points[J].Int J Math Math Sci,1991,14:451-456.

[6]Pavatham R,Radha S.Onα-starlike andα-close-to-convex functions with respect to n-symmetric points[J].Indian J Pure Appl Math,1986,16:1114-1122.

[7]Srivastava H M,Yang D G,Xu Neng.Some subclasses of meromorphically multivalent functions associated with a linear operator[J].Appl Math Comput,2008,195:11-23.

[8]Wang Z G,Gao C Y,Yuan S M.On certain subclasses of close-to-convex and quasi-convex functions with respect to k-symmetric points[J].J Math Anal Appl,2006,322:97-106.

[9]Wu Z.On classes of Sakaguchi functions and Hadamard product[J].Sci Sinica Ser A,1987,30:128-135.

[10]Xu Neng,Yang D G.Some subclasses of analytic and multivalent functions involving a liner operator[J].Math Comput Modelling,2009,49:955-965.

[11]Yang D G,Liu J L.On Sakaguchi functions[J].Int J Math Math Sci,2003,2003:1923-1931.