不規則波工況下弧形防浪墻波浪載荷試驗研究

徐 斌，劉建華，沈超明

(江蘇科技大學船舶與海洋工程學院，江蘇鎮江 212003)

不規則波工況下弧形防浪墻波浪載荷試驗研究

徐 斌，劉建華*，沈超明

(江蘇科技大學船舶與海洋工程學院，江蘇鎮江 212003)

現有關于弧形防浪墻的研究大多是針對越浪量的，對其上波浪載荷的研究涉及的不多．為彌補現有研究成果的不足并為弧形防浪墻穩定性設計提供參考，文中以復式海堤弧形防浪墻為例，以1∶15為比尺設計了不規則波斷面模型試驗．布置壓力探頭對弧形迎浪面的波壓力信號進行采集，通過積分法得出合力．通過對不規則波作用下弧形防浪墻所受波浪載荷峰值的概率分布和波浪載荷變化規律進行研究，得出:威布爾分布公式對弧形防浪墻不規則波作用下波浪載荷的概率分布進行擬合效果良好;水平波浪力、垂直波浪力和波浪力矩的最大值、2%累計頻率值以及1/3大值平均值均隨水深的增大而增大，隨波周期的增大而增大，隨波高的增大而增大．

復式海堤;弧形防浪墻;不規則波;威布爾分布;波周期;波高

港口作為交通運輸的樞紐，水陸聯運的咽喉，對我國經濟發展有著極其重要的作用．防波堤是港口及海岸防護工程中常見的一種結構型式，各種新型防波堤成為目前研究的熱門課題［1－3］，其在維護港內水域平穩和堤后生活區域安全的同時可以起到很好的景觀效果．弧形防浪墻作為一種傳統斜坡堤基礎上的新型墻結構型式，可以通過弧面的引導將波浪水體幾乎全部折返，很好地起到降低越浪的作用，從而降低堤頂高程，減少造價［4］．但是弧形防浪墻由于其結構的特殊性，波浪水體在弧面發生幾乎全部折返，堤前水體運動形態復雜，傳統的研究成果及經驗公式不能簡單地照搬運用．目前關于弧形防浪墻的研究已有不少［5－12］，但尚未有比較系統完善的結論．不規則波與實際工程所處環境最為相似，通過不規則波工況進行試驗研究弧形防浪墻波浪載荷的分布特性及其變化規律具有重要的現實意義．文中對復式海堤弧形防浪墻斷面模型試驗，通過統計分析，對不規則波作用下其所受波浪載荷峰值的概率分布和波浪載荷變化規律進行了研究．

1 試驗設備及試驗模型

試驗水槽長50 m，凈寬1.0 m，深1.5 m，一端配有消能結構，另一端為造波機．該造波機可以滿足最大工作水深0.8 m、最大波高0.45 m、試驗周期0.5～5 s的試驗要求．使用動態應變測試系統對壓力探頭信號進行采集，信號采集頻率為1 000 Hz．試驗比尺為1∶15，模型布置如圖1．

弧形胸墻內側沿高度方向均勻開設9個孔布置壓力探頭(其中弧段開孔方向為弧面的法線方向)，從上到下依次為1#，2#，…9#，為避免同一截面上開孔過密影響探頭布置和測試結果，探頭開孔采用交錯布置方式．胸墻相關尺寸及迎浪面壓力探頭布置如圖2．

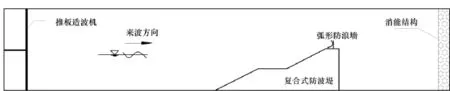
圖1 模型布置Fig．1 Model layout

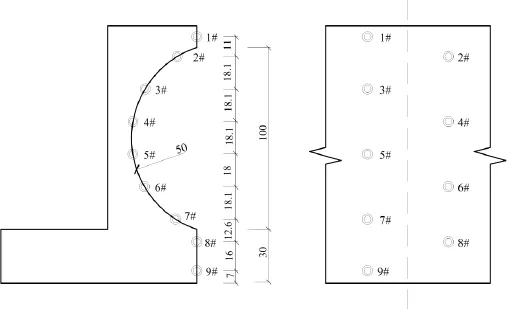
圖2 壓力探頭布置(單位:mm)Fig．2 Arrangement of pressure probes(unit:mm)

2 工況安排

試驗中不規則波波浪譜采用JONSWAP波譜:

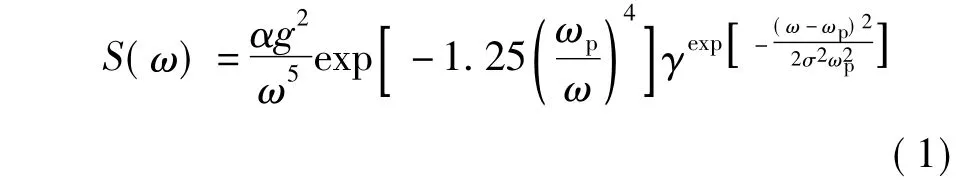
式中:g為重力加速度;ω為頻率;ωp為譜峰頻率; α為無因次常數;當ω≤ωp時，σ=0.07;當ω＞ωp時，σ=0.09;γ為譜峰升高因子，文中取3.0．

試驗組次安排如表1．

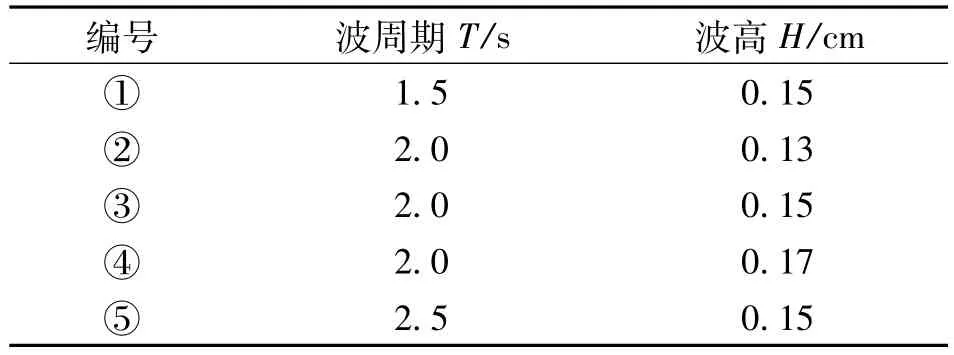
表1 波要素組合表Table 1 Amagement table of ware parameters

將各探頭壓力進行積分得到每延米弧形防浪墻模型上的水平波浪力Fh、垂直波浪力Fv以及波浪力矩M的時域t信號曲線，其中工況IR204條件下曲線如圖3(水平波浪力向防浪墻后為正，垂直波浪力向上為正，波浪力矩以防浪墻向后傾覆為正)．

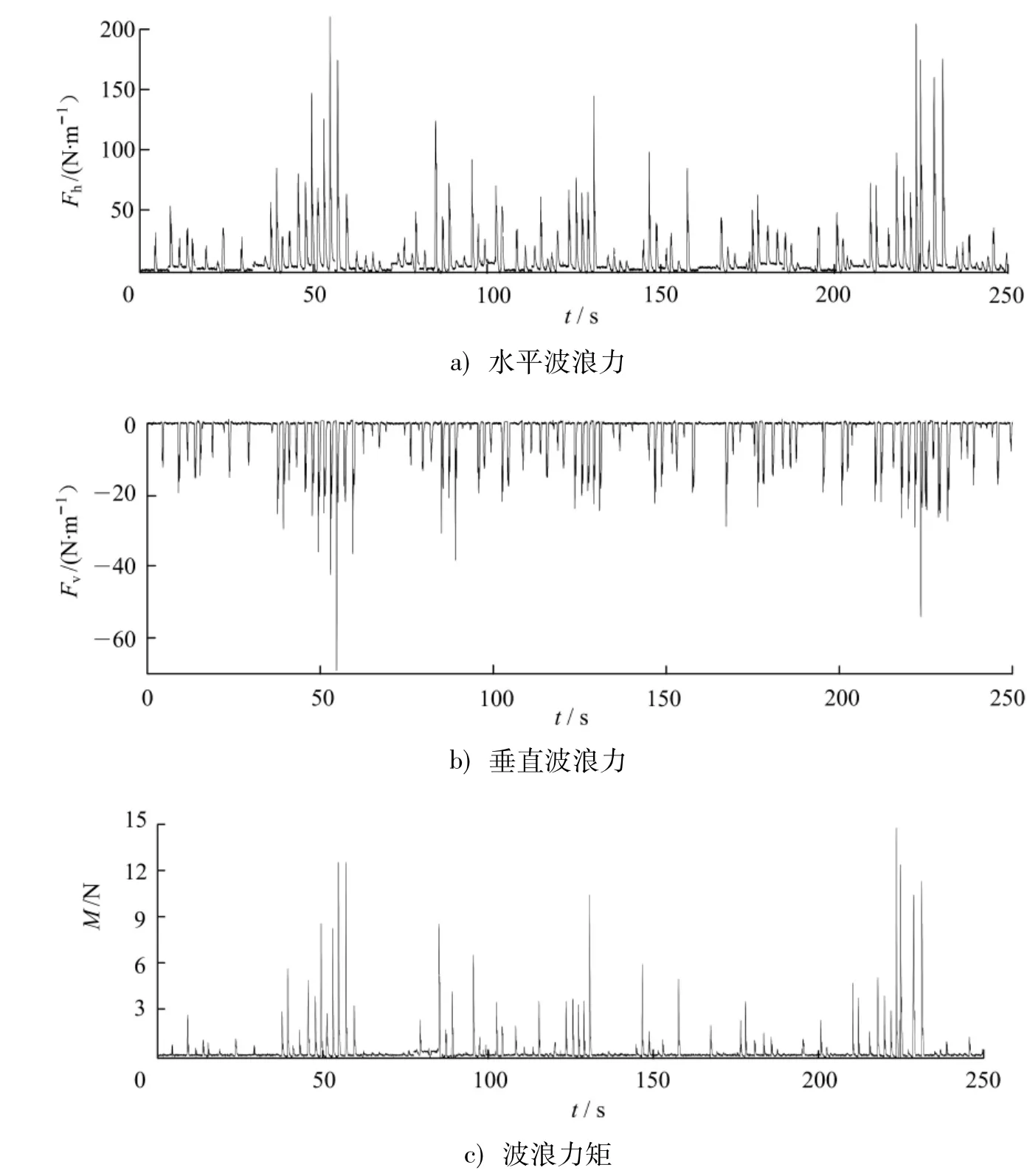
圖3 工況IR204弧形防浪墻波浪載荷時域曲線Fig．3 Signal curves of wave load on arc wave crown under condition IR204

3 波浪載荷峰值概率分布

將試驗所得波浪載荷信號統計峰值后，由大到小進行排序，排列次序為m的峰值出現的累計概率為:

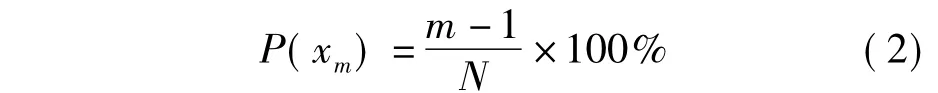
式中:xm=Fm/Fmean，Fmean為峰值統計平均值;Fm為累計概率的波浪載荷峰值;N為峰值總數．

為了對不規則波作用下弧形防浪墻波浪載荷概率分布進行最優的曲線擬合，需要將實測值所得到的累計頻率曲線與理論函數對應的曲線進行比對以選擇最適合的分布形式［13］．相關的理論分布曲線有很多，如威布爾分布、高斯分布、對數正態分布等．通過前期嘗試，威布爾分布對文中所研究的弧形防浪墻波浪載荷在不規則波作用下的累計頻率分布擬合較好，故重點采用此方法對文中不規則工況下波浪載荷的概率分布進行曲線擬合．

3.1 威布爾分布

威布爾分布在工程中應用廣泛［14］，其概率密度函數為:

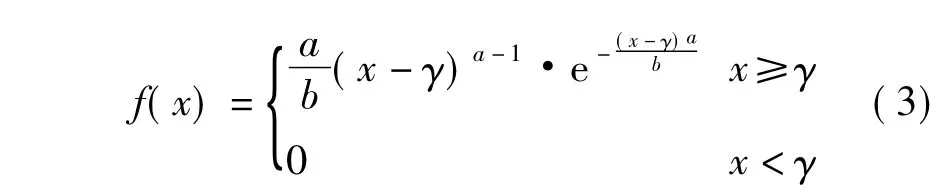
式中:a，b為威布爾函數的2個參數，a＞0為形狀參數;b＞0為比例參數;γ為位置函數，文中取為0，e為自然常數．

對式(3)進行積分簡化后可以得到其累計分布函數:

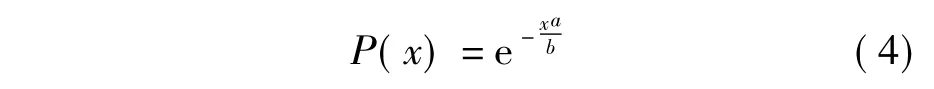
由式(4)可知:威布爾分布具有較好的適應性，使用參數a，b即可進行各種變化，當b=1時，威布爾分布轉變為指數分布當 b=2時，威布爾分布則轉變為瑞利分布．

3.2 威布爾分布相關參數擬合

通過對數變換可將式(2)轉換成線性方程的形式:

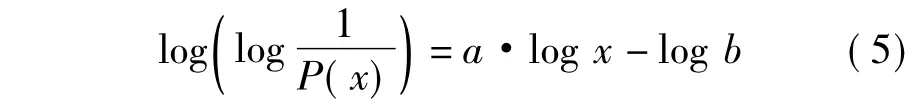
其中:Fi為累計頻率為i%的波浪載荷峰值;為波浪載荷峰值統計平均值; P(x)為累計頻率．通過Matlab對試驗數據進行擬合處理，得出參數a，b，然后繪制實測點與擬合曲線進行對比．限于篇幅，以部分工況為例，其威布爾分布擬合效果如圖4～6，d為水深．

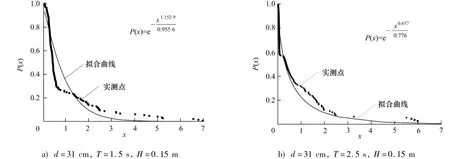
圖4 水平波浪力峰值概率分布Fig．4 Probability distribution of horizontal wave loads

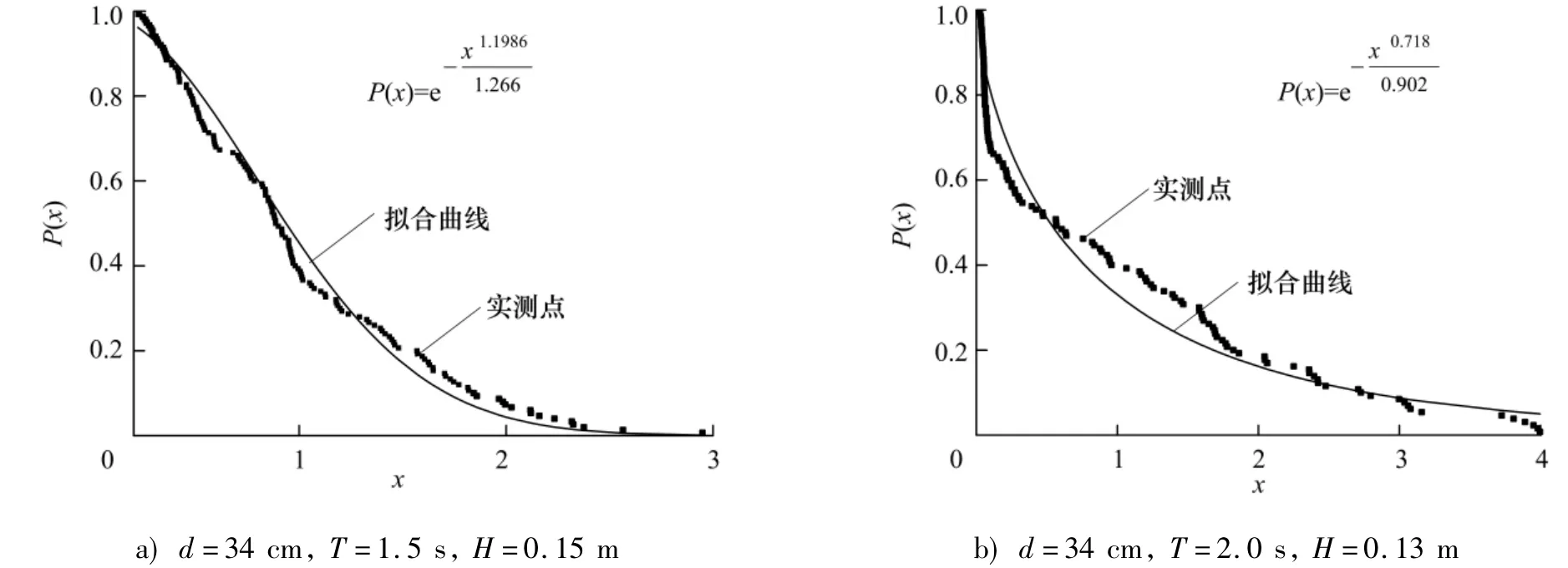
圖5 垂向波浪力峰值概率分布Fig．5 Probability distribution of vertical wave loads

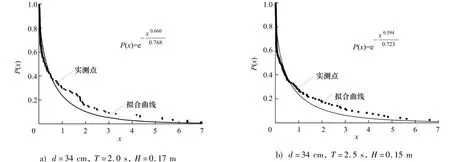
圖6 波浪力矩概率分布Fig．6 Probability distribution of wave overturning moments

通過上述分析可知:使用威布爾分布對弧形防浪墻不規則波作用下的波浪載荷的概率分布進行擬合效果良好，不同工況下擬合的威布爾參數有差異，但差別不大，參數a，b均在1上下波動．水平波浪力最大值Fhmax和波浪力矩最大值Mmax基本保持在7.0附近，垂直波浪力最大值Fvmax在3～6區間波動．

不同水深d條件下的擬合結果(參數a，b的范圍)匯總如表2所示．

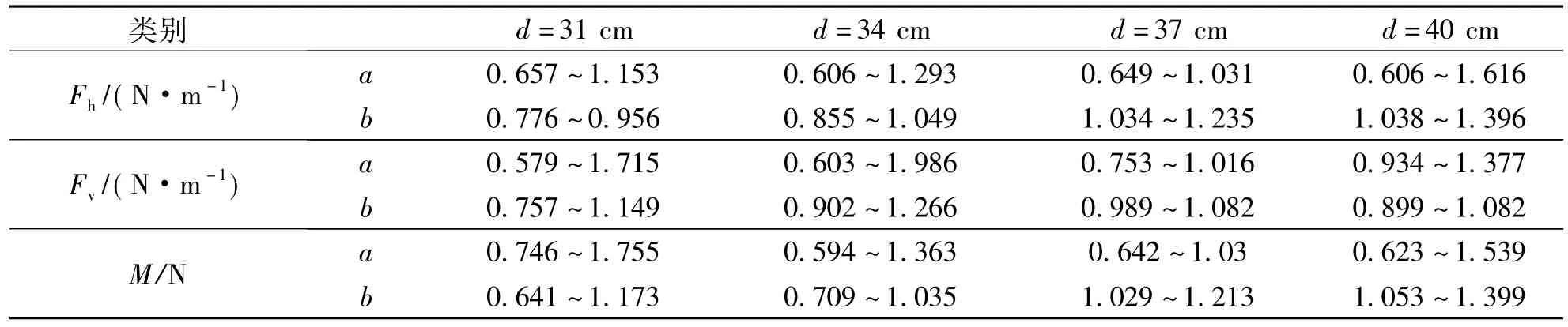
表2 參數擬合結果Table 2 Parameters fitting results

4 波浪載荷隨波要素變化關系分析

為研究不規則波條件下弧形防浪墻波浪載荷的變化規律，文中從水平波浪力最大值Fhmax、累計頻率為2%的水平波浪力Fh2%值以及水平波浪力的1/3大值平均值Fh1/33個角度進行統計分析，結果如圖7～9．

由圖7～9可以看出:在不規則波工況下，波浪載荷隨著水深的增大而顯著增大，隨波周期的增大而增大，隨波高的增大而增大，3個波浪載荷指標的最大值、累計頻率2%的值以及1/3大值平均值3個指標均可以證實．

5 結論

1)威布爾分布對弧形防浪墻不規則波作用下的波浪載荷的概率分布進行擬合效果良好，不同工況下擬合的威布爾參數有差異，但差別不大，參數a，b均在1上下波動．

2)水平波浪力最大值Fhmax和波浪力矩最大值Mmax

3)在文中所涉及的不規則波條件內，弧形防浪墻波浪載荷(水平波浪力、垂直波浪力和波浪力矩)最大值、2%累計頻率值以及1/3大值平均值均隨水深的增大而增大，隨波周期的增大而增大，隨波高的增大而增大．

4)不同累計頻率的波浪載荷可以綜合文中擬合的威布爾分布和給定波浪載荷變化關系圖進行求解．

圖7 不規則工況波浪載荷隨水深變化關系Fig．7 Graph of wave loads changing with water depth

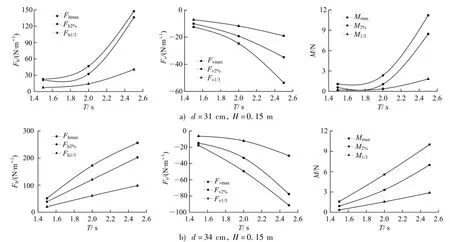
圖8 不規則工況波浪載荷隨波周期變化關系Fig．8 Graph of wave loads changing with wave period

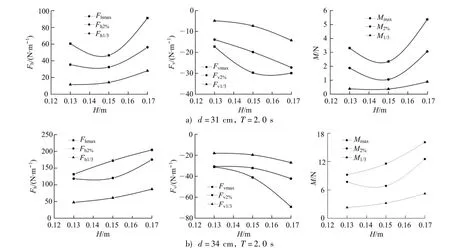
圖9 不規則工況波浪載荷隨波高變化關系Fig．9 Graph of wave loads changing with wave height

References)

［1］ 汪宏，徐洪彬，宣剛．柔性浮式防波堤的物理模型試驗研究［J］．江蘇科技大學學報:自然科學版，2013，27(2):119－122．

Wang Hong，Xu Hongbin，Xuan Gang．Physical model experimental study of flexible floating breakwaters［J］．Journal of Jiangsu University of Science and Technology:Natural Science Edition，2013，27(2): 119－122．(in Chinese)

［2］ 周效國，李雨，江沭淮，等．多層直立開孔擋板透空式防波堤消浪性能試驗研究［J］．水運工程，2014 (1):31－35．

Zhou Xiaoguo，Li Yu，Jiang Shuhuai，et al．Experiment study on wave dissipation performance of permeable breakwater of multi-layer upright wave board with holes［J］．Port＆Waterway Engineering，2014(1): 31－35．(in Chinese)

［3］ 鄭啟航，金鳳，楊強，等．框架帶孔薄膜浮式防波堤單元體［J］．中國水運，2015(5):174－175．

Zheng Qihang，Jin Feng，Yang Qiang，et al．Framework of perforated film floating breakwater unit cell［J］．China Water Transport，2015(5):174－175．(in Chinese)

［4］ 程禹平．卷波式弧形臺階海岸防浪墻［J］．海洋工程，1995，13(3):69－74．

Cheng Yuping．Curved and stepped seawall with curly wave effect［J］．Ocean Engineering，1995，13(3): 69－74．(in Chinese)

［5］ 李玉龍．不同掩護程度弧形胸墻波壓力及越浪量試驗研究［J］．海岸工程，2010，29(2):17－22．

Li Yulong．Experimental research on wave force and overtopping discharge of arc parapet with different covertures［J］．Coastal Engineering，2010，29(2):17－22．(in Chinese)

［6］ 李雪艷，任冰，王國玉，等．基于BFC-VOF方法的弧形防浪墻水動力數值模擬［J］．水道港口，2011 (4):270－275．

Li Xueyan，Ren Bing，Wang Guoyu，et al．Numerical simulation of hydrodynamic pressure on arc crown wall based on BFC-VOF method［J］．Journal of Waterway and Harbor，2011(4):270－275．(in Chinese)

［7］ 高占學，王芳．深弧型防浪墻在堤防工程中的應用［J］．水運工程，2010(3):77－80．

Gao Zhanxue，Wang Fang．Application of deep arc type flood wall in embankment engineering［J］．Port＆Waterway Engineering，2010(3):77－80．(in Chinese)

［8］ 王明英，陳利明．解析深弧型防浪墻在堤防工程中的應用［J］．中國水運，2014(7):212－213．

Wang Mingying，Chen Liming．Analytical arc type wave screens in levee engineering application［J］．China Water Transport，2014(7):212－213．(in Chinese)

［9］ 文俊超．某濱海電廠防浪墻的模型試驗與設計優化［J］．紅水河，2010(1):13－15．

Wen Junchao．Model test and design optimization of wave wall for power plant at coastal area［J］．Hongshui River，2010(1):13－15．(in Chinese)

［10］ 王穎．弧形防浪墻波浪力的試驗研究［D］．上海:上海交通大學，2007:1－79．

［11］ 王海峰，柳玉良，夏運強．有護面塊體掩護的斜坡堤弧形胸墻波壓力研究［J］．水運工程，2013(6): 16－19．

Wang Haifeng，Liu Yuliang，Xia Yunqiang．Pressure of arc parapet covered by accropodes on sloping breakwate［J］．Port＆Waterway Engineering，2013(6): 16－19．(in Chinese)

［12］ 劉佳林．直立堤弧形防浪墻波浪壓強的試驗研究［J］．中國水運，2013(4):189－191．

Liu Jialin．The experimental study on the parapet wall wave vertical embankment arc pressure［J］．China Water Transport，2013(4):189－191．(in Chinese)

［13］ 楊萍．直立堤上波谷力和傾覆力矩的試驗研究［D］．遼寧大連:大連理工大學，2013:14－18．

［14］ 王磊．基于威布爾分布的油田機采井故障率研究［D］．黑龍江大慶:東北石油大學，2014:38－40．

(責任編輯:貢洪殿)

Test research of the wave loads on arc crown wall in irregular waves

Xu Bin，Liu Jianhua*，Shen Chaoming
(School of Naval Architecture and Ocean Engineering，Jiangsu University of Science and Technology，Zhenjiang Jiangsu 212003，China)

Current researches on arc crown wall are mostly about overtopping，and only a few researches involve the wave loads on it．In order to make up for the current achievements and to provide reference for the stability design of arc crown wall，cross-section model test under irregular wave conditions is designed with the scale 1∶15，taking composite sea embankment arc crown wall as the example．Wave loads are calculated by integration of pressure signals collected through pressure probes set on the surface of the arc crown wall．The probability distribution of wave loads as well as the wave loads variation on arc crown wall in irregular waves is studied．Test results show that Weibull distribution in well with the probability distribution of wave loads on arc crown wall in irregular waves;The maximum value，the 2%cumulative frequency value and the one third big average value of horizontal wave load increase significantly with the increase of water depth，wave period and wave height，so do those of the vertical wave load and the wave moment．

composite sea embankment;arc crown wall;irregular waves;Weibull distribution;wave period; wave height

U656.3

:A

:1673－4807(2015)05－0409－07

10．3969/j．issn．1673－4807．2015．05．001

2015－07－09

徐斌(1990—)，男，碩士研究生．*通信作者:劉建華(1963—)，男，副教授，研究方向為工程力學．E-mail:jianhua-liu@163．com

徐斌，劉建華，沈超明．不規則波工況下弧形防浪墻波浪載荷試驗研究［J］．江蘇科技大學學報:自然科學版，2015，29(5):409－415．